Crucial events are generated by criticality, namely by the processes of phase transition from disorder to correlated disorder, affecting key organismal network functions. There is, as suggested by, “a subtle connection between informational exchange within and between networks and the complexity (non-simplicity) of those networks”. West and Grigolini replaced the term complexity with non-simplicity and explain their reasoning by stating that in physics it is easier to understand how phenomena function by the properties or characteristics that are missing, rather than those that are present.
- complexity
- non-crucial events
- crucial events
- FBM
- memory
- embryos
- seeds
- development
1. Introduction
In physics, a system is considered complex if it meets the anti-reductionist criterion of “the whole being greater than its parts”, but as Melanie Mitchell states in Complexity , there is really no quantitative definition of complexity [1][19], and certainly not one upon which physicists, computer-, or biological scientists agree. There does seem to be agreement that living systems exhibit complex, changing behavior at the whole organism level (macrodynamics). This complex organismal behavior emerges from the collective actions and interactions at lower levels of organization, such as among cells (microdynamics). These actions can be understood using dynamical systems theory, which can be described simply as dynamic, i.e., systems that change over time (e.g., heart beats, firing of neurons in the brain, economic markets, or global climate). Developing systems also change in space as well as time and exhibit dynamic patterns of complexity, which adapt in response to learning or external forces. For example, increasing temperature will alter rates of development and growth in fish embryos, expressed as changes in morphological [2][3][20,21] and physiological [4][22] complexity. Complex adaptive systems, therefore, are complex systems exhibiting nontrivial emergent and self-organizing behaviors [1][19], many of which result from cell-to-cell communication at many developmental levels.
2. Exploring Criticality in Developing Organisms
It is our assertion that the stable yet dynamic society of a developing organism (i.e., plant seedling or animal embryo) results from, or may be initiated by, the dynamic interplay between two patterns of information exchange or complexity. These two patterns are, (1) self-organization or non-crucial events (Fractional Brownian Motion, FBM) [5][28] and (2) crucial events (defined as events that determine the efficiency of information exchange [6][7][8][7,15,29]. The type of response depends on the interplay of a network of intracellular (within a single cell) and/or intercellular (between cells) communication and their emergent relationships with their surroundings.
Much of what we know about patterns of complexity has been learned from long time series generated from electroencephalographs (EEGs) of firing rates in the human brain [9][10][30,31], heart rate variability [11][24], and swarming birds [12][13][14][8,32,33] among others. In all these examples there are elements of nonlinear interactions, which result in measurable patterns and modes known as phase transitions where there is a dynamic balance between order and randomness, and crucial events. Crucial events in the above situation are also referred to as renewal events, which are events that reset the memory of the system, erasing the memory of, and independent of, earlier events [7][8][10][15,29,31].
Many complex processes can be characterized by crucial or renewal events and all are independent of the underlying microdynamic emergent behaviors that can be localized in time. In [15][6] the authors clearly laid out that probability distribution densities (pdd) of the time distance, between two consecutive renewal events, which is given by the waiting time distribution ψ τ and written as an inverse power law,
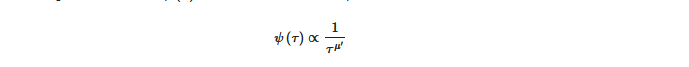
where μ is the complexity index which can range from 1 to ∞ , with complexity occurring when 1 < μ < 3. The breakdown in the ergodicity of a complex system for μ < 2 is a direct result of the occurrence of crucial events. However, if an event occurs at a specific time, after which subsequent events are produced, it is time dependent and the ψ τ has a hyperbolic form, see [7][15] for a more detailed discussion. As is stated in [15][6] μ < 3 suggests a departure from the condition of ordinary statistical physics to nonlinear statistical physics. Further, crucial events can arise spontaneously in complex systems, in keeping with the theory of self-organized temporal criticality (SOTC) [6][16][17][18][19][7,9,34,35,36] which posits that a system of interacting units may spontaneously generate temporal complexity, that is self-organized criticality (SOC) characterized by crucial events in time [15][6] in which μ is not limited to merely the non-ergodic regime of μ < 2 but extends to the whole complexity range of 1 < μ < 3.
In a developing organism, formation of an orderly multicellular network from relatively homogenous material in a single cell is the result of transactions among nonlinear, self-similar and self-organized components. Those transactions are generally known as cell-to-cell communication and operate based on an inducer (e.g., a cell that produces a signal) and a responder (a cell that responds to the signal by changing some behavior). Successful communication takes place when competence occurs, i.e., when a signal results in a response. We will now consider the processes that are understood to regulate cell-to-cell communication and highlight some of the gaps. These gaps in knowledge about cell-to-cell communication may be where information transfer and crucial events could play a part in directing development of coordinated causal multicellularity.
3. Cell-to-Cell Communication, Complexity and Self-Organization
While development is a process that occurs in all organisms, it is concerned with more than just cellular differentiation because different cell types of an organism do not exist in random arrangements. In the mid-twentieth century two biologists, Townes and Holtfreter [20][37] predicted that embryonic cells could have differences in the components of their cell membranes which allowed them to form organs. Now we understand that formation of organs is a result of cell-to-cell communication achieved through biochemical molecules that are secreted or located in the cell’s membrane. These ‘informational’ molecules can bind to receptors on neighboring cells and stimulate a signaling cascade of intracellular reactions, which results in changes in gene expression, enzymatic activity, and cytoskeletal organization, affecting cell shape and cell behavior. However, it should be mentioned that even at the biochemical level, cell-to-cell communication is much more complicated than suggested above. In addition to signaling cascades with the cell, there are also important intercellular secretory products that trigger cellular responses. These responses are typically ligand–receptor based and range from long distance (endocrine) hormones that travel through the blood stream to short distance (paracrine factors e.g., FGFs) that diffuse between cells across the extracellular matrix (ECM) to target receptors on the cell membrane. Also important to cell-to-cell communication are adhesion molecules that mediate the interactions between cells and the ECM, are critical for maintaining cell structure and function, and are key to organization of cells into tissues and organs.
Following fertilization, the process of cleavage transforms a single cell into a multicellular organism containing hundreds of cells (e.g., the nematode worm C. elegans contains 946 cells) or trillions of cells in an adult human being. These different cell types then work together to form a biologically complex, coherent, functional organism that can respond to change and exhibit a degree of resilience [21][38]. Physical (free diffusion, osmosis, viscosity, elasticity, and viscoelasticity) and cellular processes (mentioned above) act on single cells and take part in acts of aggregation and adhesion to form multicellular systems (tissues) and in the process they ‘re-enact ’ the development of cell-to-cell communication systems that emerged 1.5 billion years ago [21][38]. This means biochemical and energetic processes involved in cell-to-cell communication that first evolved 1.5 billion years ago are conserved, remaining essentially unchanged over evolutionary time. This then begs the question that if there are, as we suggest in this paper, informational exchange mechanisms also critical for development, might they too also have been conserved? During later stages of development, when organization of tissues and organs is taking place, the embryo stays in a relatively stationary state of reduced information (entropy) exchange that is maintained for extended periods of time, making self-organizing or autopoesis of living matter possible [22][39]. Autopoesis is understood to be any increase in the order within the system (i.e., production of negentropy) and is possible only if high internal biological organization through cell-to-cell communication exists [23][40].
Kauffman, in his landmark paper [24][41] stated that a fundamental task of biology is to account for the origin and nature of metabolic stability in living systems in terms of the mechanisms that control biosynthesis. Kauffman stated that biosynthesis includes the renewal or new production of cells resulting from a state of disorder through mitosis (which includes both DNA replication and cell division). He goes on to contrast order and chaos as interpreted in physics and then in biology. In physics when considering the thermodynamics of gases, the mathematical laws of statistics bridge the gap between the randomness of colliding molecules and the simplicity of the gas laws. Whereas in biology a gene can specify a protein and that protein can, in turn, control the expression and or repress another gene [25][42]. In living organisms, mathematical laws also engage large networks (referred to as gene regulatory networks (GRNs)) of interacting genes to bring biosynthetic or biological self-organization from disorder.
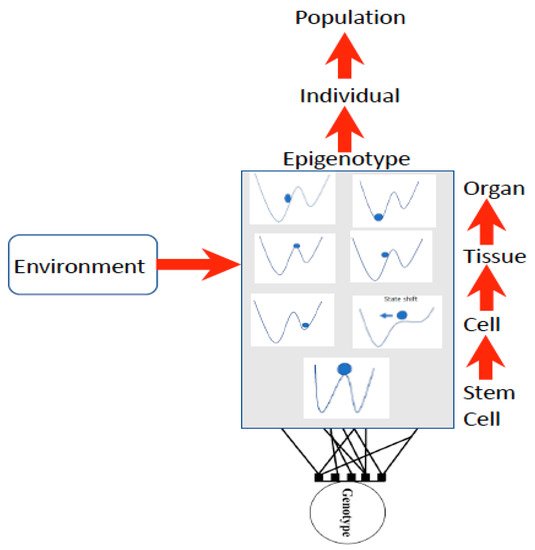
Waddington used the stability landscape to describe the cellular development where the cell was represented as the ball at the top of the landscape ( Figure 12 ). The paths available to the ball (or features of the landscape) are determined by the genotype, interactions among cells, tissues, organs, and the environment [12][26][8,49], forming what is referred to as the epigenotype (epi- or above-the-genotype). Epigenetics can include all effects and modifications that are dependent on genetic factors, such as DNA sequences, but may increase or decrease phenotypic (observable traits) variation expressed by target sequences in response to environmental cues, or emergent interactions during development [27][28][50,51]. The epigenotype can integrate information from external sources and influence development to produce a cohesive (coherent or stable) organism that will adapt to its environment by responding to change.
4. Measuring Complexity Using Ultraweak Photonic Emission (Upes)/Biophotons
, of 0.77 ± 0.03 with a variance (σ
) of 0.001, which corresponded to a mean μ = 2.30 ± 0.05 with a σ
of 0.002. While in the second set of three regions (regions #4–6,
), there was a mean ± SD scaling index of η of 0.72 ± 0.02 with a σ
of 0.0005, which corresponded to a mean μ = 2.39 ± 0.04 with a σ
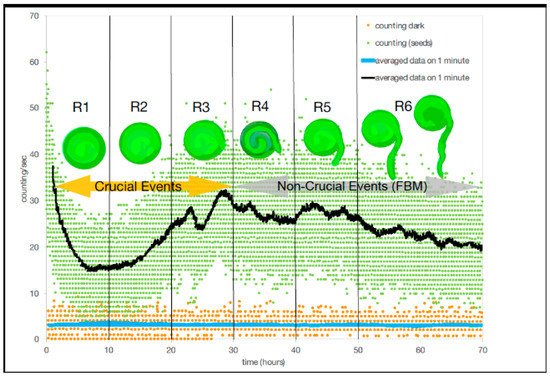
of 0.002. Thus, DEA without stripes could not distinguish between crucial events and FBM (
3). In contrast, when applying the use of stripes to DEA, the results showed a clear and significant time dependence in the first three temporal regions where the mean scaling parameter of η ± SD is 0.56 ± 0.04, and a variance of 0.001, which corresponds to a mean μ ± SD, 2.79 ± 0.11 with a σ
of 0.012 (
). While in the second three regions (regions #4–6,
), there was a mean ± SD of the scaling index of η of 0.503 ± 0.01 with a σ
of 0.00006, which corresponded to a mean μ = 2.99 ± 0.03 with a σ
of 0.0007. For DEA with stripes, results indicated that crucial events exist in the first three temporal regions (#1–3) and non-crucial events dominate in the last three temporal regions (#4–6). Although, as Benfatto et al. [6] explained that there was the possibility of no crucial events and that anomalous scaling (with the significant difference from ordinary scaling η
| Without Stripes | With Stripes | |||
|---|---|---|---|---|
| η | µ | η | µ | |
| Dark Counts | 0.575 | 2.739 | 0.508 | 2.968 |
| 1 | 0.777 | 2.293 | 0.596 | 2.677 |
| 2 | 0.796 | 2.254 | 0.558 | 2.792 |
| 3 | 0.736 | 2.358 | 0.526 | 2.901 |
| 4 | 0.737 | 2.355 | 0.496 | 3.016 |
| 5 | 0.694 | 2.440 | 0.509 | 2.964 |
| 6 | 0.725 | 2.377 | 0.504 | 2.984 |
