The global system is illustrated in Figure 1. It is based on a WT-DFIG system, directly interconnected to the AC grid by the DFIG stator. On the other side, its rotor is attached via an indirect converter from the grid. It consists of two power converters, which are connected to DC bus. The first converter (I) is an inverter of three levels attached to the DFIG rotor, and the second converter (II) is attached to the grid and controlled by another method. The second converter controls its output to obtain a unit power factor operation, sinusoidal voltages, and currents with a constant frequency.
- grid-connected wind turbine conversion
- random behavior wind speed
1. Wind Turbine Working Zones Description
The wind turbine with variable speeds works in different operating zones as presented in [1]. Zone I is a region where the wind speed is low, to begin the energy production for economic reasons. Zone II is where the WT receives wind with a speed bigger than cut-in speed, the system works with MPPT algorithm to extract maximum power with null angle pitch. Zone III is described as when the wind speed exceeds the nominal operation mode; the system works under pitch angle control to limit the produced output power to its nominal value by varying angle pitch β. In zone IV, once the maximum wind speed is reached, the DFIG rotor is disconnected from the turbine, therefore interrupting the power generation [1].
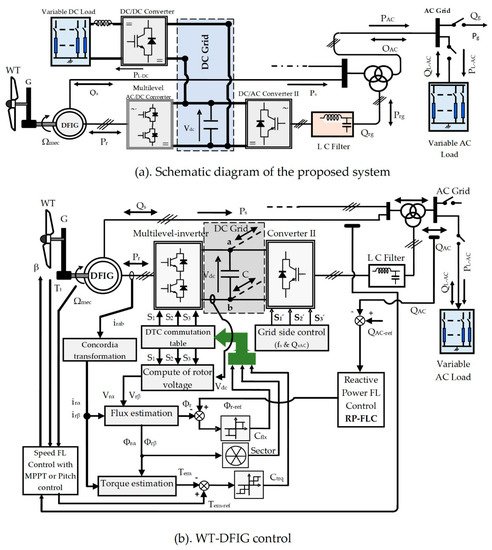
Figure 1.
2. Maximum Power Point Tracking Description
p-max
opt) and a null blade angle (β = 0°) [1][2]. The speed of the DFIG is enslaved to a reference from an MPPT algorithm for maximum tracking of wind power.
3. Pitch Angle Control Description
In zone III, the control of WT angle blades limits the delivered power to its nominal value when the system works overspeed, while the extraction power maximization means that the power produced is regulated according to its speed, in order to protect the power converters and the electrical generator, so the PI regulator insures the generation of Tem-ref to increase the blade angle (β), keeps the power at the nominal value, and decreases the speed ratio (λ) and the power coefficient (Cp) [1].
) [18].4. Description of the Proposed Direct Reactive Power Control
4.1. Direct Torque Control of the Three-Level Inverter Description
Reference [3] describes the characteristic of the wind turbine and the operating zones from which the principles of MPPT and pitch control are taken.
The DTC of the DFIG is based on the control of the rotor flux and the value of the electromagnetic torque. The rotor flux and the electromagnetic torque are estimated from the rotor flux components along the α and β axes [3][1], as given in Equations (1) and (2).
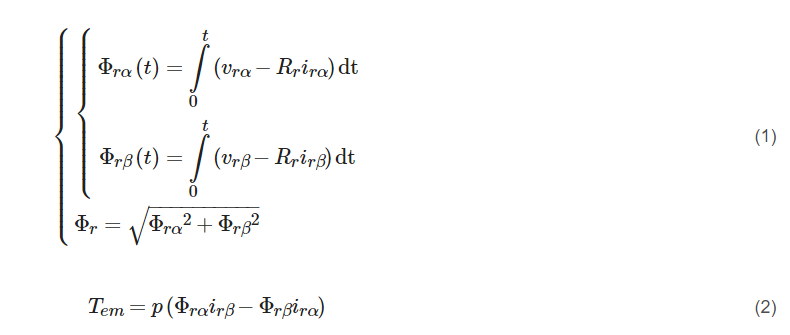
Vdc
/2, 0 and −Vdc
/2). The transformation of voltages from the natural three phases into bi-phases (α-β) gives voltage vectors associated to the stator flux position. The vector’s various state number is 19 since some of the 27 possibilities yield the same voltage vector. The presentation of all voltage vectors of the three-level inverter in the bi-phasic frame is shown inFigure 2
.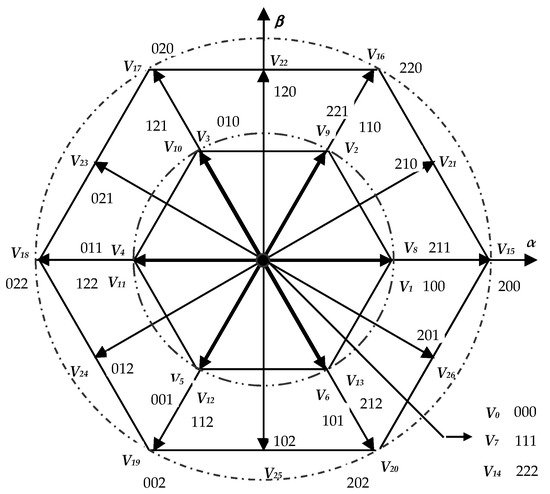
Figure 2.
Figure 2
. The implementation of DTC to the studied system is accomplished by selecting the optimal vector and applying it to the three-level inverter. In order to establish the control with the proposed topology, first, the estimated values of torque and flux are compared with the references, and then the errors are digitized out of the hysteresis regulators, five-level and three-level comparators, respectively, which gives the variable flux (Cflx
) and the variable torque (Ctrq
). The number of sector N is determined using the α-β rotor flux component. If the torque comparator output is high or equal to two, the inverter state is considered high, otherwise the state is considered low. For the torque regulation, the use of a five-level hysteresis comparator permits the ability to have both rotation directions of the rotor flux compared to the stator flux. The output of this regulator is represented by a Boolean variable,Ctrq
, indicating if the torque needs be raised (Ctrq
= 2 or = 1), reduced (Ctrq
= −2 or = −1), or kept constant (Ctrq
= 0). For rotor flux control, a three-level hysteresis comparator could be used. Therefore, the rotor flux magnitudeΦr
is able to be controlled. The output of the flux regulator is also represented by a Boolean variable,Cflx
, indicating if the flux needs be raised (Cflx
= 1), reduced (Cflx
= −1), or kept constant (Cflx
= 0) to preserve it: |Φr_ref
−Φr
| ≤∆Φr
. The switching table of the three-level inverter DTC is presented inTable 1
. This table is considered to select the appropriate vector using the information described above (numerical errors of fluxCflx
and torqueCtrq
, and the number of sector N). When the impact of each voltage vector is analyzed, it may be observed that the vector impacts the torque and flux with the modulus and vector direction changes. The null voltage vectors (V0
,V7
, andV14) are selected alternately, in order to minimize the number of switches in the inverter arms [4].
) are selected alternately, in order to minimize the number of switches in the inverter arms [23].Table 1.
DTC
| Cflx | Ctrq | N | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||
Figure 4
Table 2
Table 3 for the second regulator F-PD. Finally, the method of center of gravity (CoG) is invested for the defuzzification of both FLCs as its the most commonly used defuzzification method, also commonly referred to as the centroid method. This method determines the center of area of a fuzzy set and returns the corresponding crisp value [5][2].

Figure 4.
Table 2.
| de/e | NL | NM | NS | ZR | PS | PM | PL |
| NL | NL | NL | NL | NL | NM | NS | ZR |
| NM | NL | NL | NL | NM | NS | ZR | PS |
| NS | NL | NL | NM | NS | ZR | PS | PM |
| ZR | NL | NM | NS | ZR | PS | PM | PL |
| PS | NM | ||||||
| PL | |||||||
| PL | ZR | PS | PM | PL | PL | PL | PL |
Table 3.
| de/e | NL | NM | NS | ZR | PS | PM | PL | |||||||
| NL | NL | NL | NL | NL | PS | PS | PS | |||||||
| NM | NL | NL | NL | NM | PS | PS | PS | |||||||
| NS | NL | NL | NM | NS | PS | PS | PM | |||||||
| ZR | NL | NM | NS | ZR | PS | PM | ||||||||
| NS | ZR | PS | PM | PL | PL | |||||||||
| PL | ||||||||||||||
| PS | NM | NS | NS | PS | PM | PL | PL | PM | NS | ZR | PS | PM | PL | PL |
| PM | NS | NS | NS | PS | PM | PL | PL | |||||||
| PL | NS | NS | NS | PS | PL | PL | PL | |||||||
| +1 | +2 | V21 | V16 | V22 | V17 | V23 | V18 | V24 | V19 | V25 | V20 | V26 | V15 | |
| +1 | V21 | V2 | V22 | V3 | V23 | V4 | V24 | V5 | V25 | V6 | V26 | V1 | ||
| 0 | Zero vector | |||||||||||||
| −1 | V26 | V1 | V21 | V2 | V22 | V3 | V23 | V4 | V24 | V5 | V25 | V6 | ||
| −2 | V26 | V15 | V21 | V16 | V22 | V17 | V23 | V18 | V24 | V19 | V25 | V20 | ||
| −1 | +2 | V17 | V23 | V18 | V24 | V19 | V25 | V20 | V26 | V15 | V21 | V16 | V22 | |
| +1 | V3 | V23 | V4 | V24 | V5 | V25 | V6 | V26 | V1 | V21 | V2 | V22 | ||
| 0 | Zero vector | |||||||||||||
| −1 | V5 | V25 | V6 | V26 | V1 | V21 | V2 | V22 | V3 | V23 | V4 | V24 | ||
| −2 | V19 | V25 | V20 | V26 | V15 | V21 | V16 | V22 | V17 | V23 | V18 | V24 | ||
| 0 | +2 | V22 | V17 | V23 | V18 | V24 | V19 | V25 | V20 | V26 | V15 | V21 | V16 | |
| +1 | V22 | V3 | V23 | V4 | V24 | V5 | V25 | V6 | V26 | V1 | V21 | V2 | ||
| 0 | Zero vector | |||||||||||||
| −1 | V25 | V6 | V26 | V1 | V21 | V2 | V22 | V3 | V23 | V4 | V24 | V5 | ||
| −2 | V25 | V20 | V26 | V15 | V21 | V16 | V22 | V17 | V23 | V18 | V24 | V19 | ||
4.2. The Proposed Fuzzy PID Design and Local Reactive Power Compensation Description
Figure 3
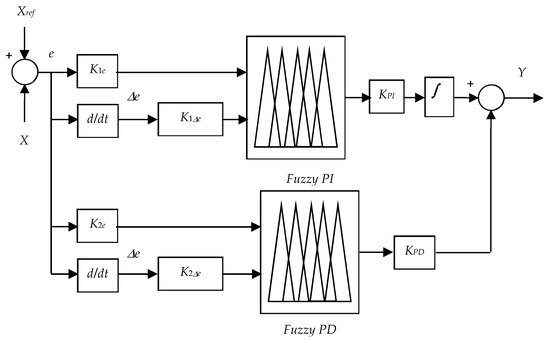
Figure 3.
Ω
ref
Ωref
Tem-ref
QAC
ref
QAC-ref
(Φr-ref
K1e
K1Δe
PI
K2e
K2Δe
PD
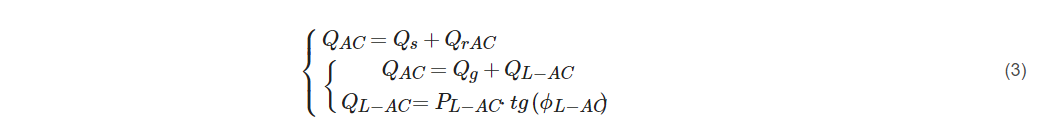
Qs
QL-AC
QAC
Qrg
ϕL-AC
