Generation/Amplification of Mid-Infrared Few-Cycle Pulse: Comparison
View Latest Version
Please note this is a comparison between Version 2 by Lindsay Dong and Version 1 by Houkun Liang.

The mid-infrared (MIR) wavelength is usually defined in the range of 2–20 μm (500–5000 cm−1). With its unique properties and wide application prospects, lasers in this band have attracted a great deal of attention from researchers all over the world.

  • mid-infrared
  • few-cycle pulse
  • optical parametric amplification
  • optical parametric chirped-pulse amplification
  • intra-pulse difference-frequency generation

1. Introduction

The main characteristics of an MIR laser can be summarized as the following two aspects. First, as the pondermotive energy is quadratically proportional to the driving laser wavelength, MIR lasers with high peak power have been routinely pursued as the driving sources for novel strong-field phenomenon [1,2,3[1][2][3][4][5][6][7][8][9],4,5,6,7,8,9], such as extreme ultra-violet and X-ray generation [10[10][11][12][13],11,12,13], attosecond pulse generation [14], and terahertz generation [15,16,17][15][16][17]. Second, most of the vibrational peaks of different molecules fall in the MIR band, which is also called the “molecular fingerprint” regime. Therefore, MIR coherent spectroscopy is a unique method for high-fidelity and high-sensitivity molecule detection and identification [18,19,20,21,22,23,24][18][19][20][21][22][23][24].

As for MIR solid-state lasers, there are two main technique streams to generate MIR pulses, namely the direct emission of doped ions and optical parametric down conversion. The former is based on a process wherein the gain medium is stimulated after energy storage, and the output wavelength depends on the energy level structures of the gain media. The biggest challenge of this process is that the relaxation energy in the MIR wavelength coincides with the phonon vibration energy, which reduces the gain and hinders the lasing process at the MIR wavelength. The second technique is based on the parametric frequency conversion that is mainly assisted by nonlinear crystals that create the phase-matching conditions. In this process, there is no thermal accumulation, and broadband laser amplification can be realized through broadband phase matching, which supports the generation of few-cycle MIR pulses. At present, parametric down conversion has become an indispensable means to expand the new laser spectrum, generating pulses covering deep ultraviolet, visible, near-infrared, MIR, and THz wavelength regimes.

2. MIR Nonlinear Crystals

Nonlinear crystals that are commonly used in MIR pulse generation and amplification mainly include KTiOAsO4 (KTA), KTiOPO4 (KTP), and LiNbO3 (LNO), which belong a group known as oxide crystals, and ZnGeP2 (ZGP), CdSiP2 (CSP), AgGaS2 (AGS), AgGaSe2 (AGSe), GaSe, BaGa4S7 (BGS), BaGa4Se7 (BGSe), LiGaS2 (LGS), and LiGaSe2 (LGSe), which are classified as non-oxide crystals. Generally, the damage threshold and mechanical hardness of oxide crystals are excellent, but their transparent range is limited to less than 5 µm, which is not conducive for the generation of long-wavelength MIR pulses. The effective nonlinear coefficient of non-oxide crystals is higher, and the transparency range can reach more than 10 µm, which is commonly used in the generation of long-wavelength infrared pulses. However, the bandgap energy of such crystals is generally around 2 eV, which makes the two-photon absorption non-negligible, and significantly reduces the damage threshold when pumped at an ~1 µm wavelength with high peak power. LGS and LGSe are relatively new MIR nonlinear crystals with large bandgap energy, which enables high peak power pump at an ~1 µm wavelength. However, the transparent range of LGS and LGSe are limited to 10 µm. High quality new MIR nonlinear crystals with large bandgap energy and a broader transparent range are desired. BGSe is one of the candidates, however, the crystal growth quality still needs substantial improvement. In addition to the above MIR nonlinear crystals, periodically poled crystals such as periodically poled LiNbO3 (PPLN), orientation-patterned GaAs (OP-GaAs), and orientation-patterned GaP (OP-GaP) have become an emerging stream in the MIR parametric down conversion with their excellent quasi-phase matching bandwidth and large nonlinear coefficients, although their aperture size is the current bottleneck for pulse energy upscaling.

3. MIR Generation

Among all kinds of nonlinear polarizations, the most commonly used in down conversion is probably the second-order nonlinear effect due to the good efficiency. The three-wave mixing process introduced by the second-order nonlinear effect is the basis of second harmonics generation (SHG), difference-frequency generation (DFG), and OPA. DFG and OPA are the main methods of broadband MIR pulse generation and amplification. In a further step, combined with the theory of OPA and chirped-pulse amplification (CPA) technologies, OPCPA have emerged to scale up the pulse energy and peak power of MIR few-cycle lasers.

3.1. OPA

OPA is an old parametric technique with emission in the visible and near-infrared wavelength regimes. It has the merits of broadband emission and simple dispersion control. Recently, the OPA emission bad has been extended to MIR wavelengths pumped at ~1 and ~2 µm wavelengths, as summarized in Table 21.

Table 21.
Parameters of selected OPA system pumped by 1 and 2 µm.
318
15.1
[
37
]
[
29]
In 2020, Heiner et al. presented an OPA system pumped by a Yb:KGd(WO4)2 laser system with a repetition rate of 100 kHz and pulse width of 180 fs at 1028 nm [33][25]. The pump was divided to produce white light as the seed of the amplification stage, where the crystal could be BGS or LGS with large bandgap energy. After the Ge lens, average pulse power of 59 mW at 10 µm and 81 mW at 8.1 µm through the BGS and LGS crystals of the same length respectively were obtained, and their pulse widths were measured as 126 fs (3.8 cycle) and 121 fs (4.5 cycle), as shown in Figure 51. This comparison indicates that BGS is a promising candidate for 1-µm-pumped OPAs generating MIR emission beyond 5 µm because of its larger size availability and longer transmission cutoff up to 13.7 µm.
Photonics 08 00290 g005 550
Figure 51. Illustration of BGS OPA laser system. BS, beam sampler; PR, partial reflector; WLC, white light continuum generation unit; L, lens; BD, beam dump. DM1, dichroic mirror, high reflection (HR) at 1.03 µm and high transmission (HT) at >1.1 µm; DM2, dichroic mirror, HR at 1.0–1.2 µm and HT at 6–12 µm; OPA, LGS or BGS crystal; Ge, germanium-based temporal chirp compensation unit. Reprinted with permission from [33][25].

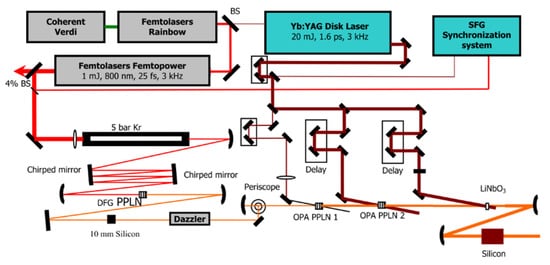
3.2. MIR OPCPA

3.2.1. 2–4 µm OPCPA

OPCPA systems have superior energy and power upscaling capability. With careful dispersion management, amplified pulses with a pulse width close to the transform limit could be generated. High-energy, few-cycle light sources with a central wavelength of 2–4 µm, and multi-millijoule pulse energy have been realized in many research groups via OPCPA techniques. Table 32 summarizes the specifications of few-cycle 2–4 µm OPCPA.

Table 32.
Parameters of selected 2–4 µm OPCPA system.
[
49
]
[
40
]
3.4
0.012
50 0.6 41.6 3.7 [50][41]
3.425 13.3 0.01 0.133 111 9.7 [51][42]
3.9 8 0.02 0.16 83 6.4 [52][43]
4 2.6 0.1 0.26 21.5 1.6 [53][44]
In a pioneer work, F. Krausz’s research group employed the broadband Ti:sapphire laser (oscillator and amplifier) as both the signal and pump at the same time [39][30]. As shown in Figure 62, the 1030 nm component of the broadband spectrum output from the Ti:sapphire oscillator was extracted and injected into a Yb:YAG thin disk amplifier to obtain the pump light synchronized with the signal beam. Non-collinear OPAs (NOPAs) were carried out in two stages using PPLN crystals and during the last power amplifier stage with a LNO crystal. Finally, a MIR output at a central wavelength of 2.1 µm and a repetition frequency of 3 kHz with a pulse energy of 1.2 mJ and a pulse width of 10.5 fs (1.5 cycles) was obtained.
Photonics 08 00290 g006 550
Figure 62. Schematic of 2.1 µm few-cycle OPCPA system. Reprinted with permission from [39][30].

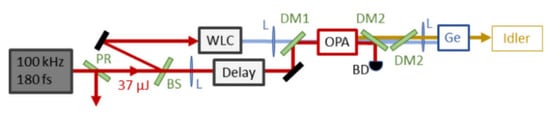
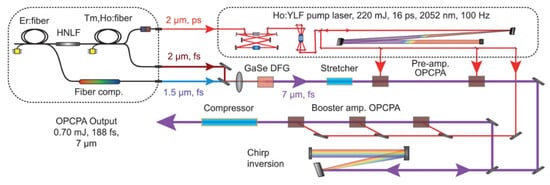
3.2.2. 5–10 µm OPCPA

In recent years, there have been emerging reports of long-wavelength MIR OPCPA systems with lasing wavelengths exceeding 5 µm. Table 43 summarizes long-wavelength MIR OPCPA systems with the centre wavelengths of 5 µm, 7 µm, and 9 µm.
Table 43.
Parameters of the long-wavelength MIR OPCPA systems.
Wavelength

(μm)		 Pulse Energy

(mJ)		 Repetition Rate

(kHz)		 Power

(W)		 Pulse Width

(fs)		 Optical Cycle Reference
5 3.4 1 3.4 89.4 5.4 [54][45]
7 0.7 0.1 0.07 188 8 [55][46]
9 0.014 10 0.14 142 4.7 [56][47]
In 2016, J. Biegert’s team demonstrated a high-energy, few-cycle 7 µm OPCPA [55][46]. As shown in Figure 13, the system started with an Er:Tm:Ho:fiber laser which generated a 7 µm seed via DFG in a CSP crystal. The 7 µm seed pulse was then amplified in a ZGP-based OPCPA chain pumped by a cryogenic-cooled Ho:YLF CPA system with a 260 mJ pump energy at 2052 nm and a 16 ps pulse width. The pulses were first put through both a pre-amplifier and booster amplifier stage, and finally put through a compressor, after which a 7 µm pulses with a 0.75 mJ pulse energy and a 188 fs pulse width were obtained.
Photonics 08 00290 g013 550
Figure 13. Layout of the 7 µm OPCPA. The MIR seed was generated using the two broadband femtosecond outputs from a three-color fiber frontend via DFG. Afterwards, the MIR pulses were stretched in a dielectric bulk and consecutively amplified in a pre-amplifier and a booster amplifier separated with a chirp inversion stage. Maximum efficiency of the OPCPA was achieved by tailoring the seed-to-pump pulse durations in the pre-amplifier and booster amplifier. The broadband high-energy MIR pulses were recompressed using a dielectric bulk rod of BaF2. Reprinted with permission from [55][46].

3.3. MIR Intra-Pulse DFG

DFG has remarkable advantages such as a single pass structure without complex cavity adjustment and a broad tuning range of the output spectrum. Intra-pulse DFG (IPDFG) is a special DFG process that uses the low and high frequency components of an ultra-broadband pump pulse to realize MIR femtosecond emission. In this method, only an ultra-broadband pump laser with a few-cycle pulse width is needed, which further simplifies the DFG process. Table 54 lists the state-of-the-art work that have generated few-cycle MIR laser pulses.
Table 54.
Parameters of selected IPDFG source.
Pump Wavelength

(µm)		 Nonlinear Crystal IPDFG Spectral Span

(µm)		 Conversion Efficiency

(%)		 Reference
1.03 LGS 8–11 0.037 [58][48]
1.03 LGS 6.8–16.4 0.11 [59][49]
1.57 OP-GaP 4–12 0.071 [24]
1.9 GaSe 3.7–18 1.4 [60][50]
2 ZnSe 2.7–20 0.51 [61][51]
2 GaSe 4.5–20 0.13 [62][52]
2.1 AGSe 7–11 0.8 [63][53]
2.5 GaSe 4.3–17.6 0.22 [64][54]
2.5 ZGP 5.8–12.5 3.3 [64][54]
3 GaSe 6–13.2 5.3 [65][55]
Wavelength

(µm)		 Pulse Energy

(mJ)		 Repetition Rate

(kHz)		 Power

(W)		 Pulse Width

(fs)		 Optical Cycle Reference
2.1 1.2 3 3.6 10.5 1.5 [39][30]
2.1 2.7 10 27 30 4.3 [40][31]
2.1 2.6 1 2.6 39 5.6 [41][32]
2.2 0.25 100 25 16.5 2.2 [42][33]
2.5 0.126 100 12.6 14.4 1.7 [43][34]
3 0.3 10 3 21 2.1 [44][35]
3 2.4 10 24 50 5 [45][36]
3.07 0.01 125 1.25 72 7 [46][37]
3.1 0.125 100 12.5 73 7 [47][38]
3.2 0.152 100 15.2 38 3.6 [48][39]
3.25 0.06 160 9.6 14.5 1.4
J. Zhang et al. demonstrated few-cycle pulse generation by means of the soliton self-compression of the pump pulse in a silica-core photonic-crystal fiber, and subsequently, LWIR generation using IPDFG, resulting in a two-octave-spanning spectrum (−30 dB) from 5 to 20 µm at an average power of 24 mW, as shown in Figure 174 [62][52].
Photonics 08 00290 g017 550
Figure 174. (a) Self-compression and MIR generation setup. (b) MIR spectrum and beam profile. The MIR spectrum (red line) together with the noise floor (gray line) measured using a monochromator. The MIR spectrum extends from 500 cm−1 to 2250 cm−1 (−30 dB), corresponding to the wavelength range from 4.5 to 20 µm. Inset: the beam profile measured using a Pyrocam beam profiler. Reprinted with permission from [62][52].

4. Single-Cycle MIR Generation

High energy single- or sub-cycle MIR pulses can provide unique opportunities to explore phase-sensitive strong-field light-matter interactions in atoms, molecules, and solids. Tremendous efforts have been made to reduce the duration of a laser pulse down to a few-cycle or to the single-cycle regime. Obtaining such an ultrashort laser pulse requires spectral broadening and phase control over the ultrabroad spectrum that supports a single-cycle pulse. At present, four methods have been used to generate single-cycle MIR pulses, namely DFG, four-wave mixing (FWM), OPA, and IPDFG. Table 65 shows several works that have generated single- or sub-cycle MIR pulses.

Table 65.
Parameters of single- or sub-cycle MIR.
Method Wavelength (µm) Repetition Rate

(kHz)		 Pulse Energy (µJ) Pulse Width (fs) Optical Cycle Reference
DFG 5–300 1 0.4 46 1 [67][56]
3–18 1 2 45 1.2 [68][57]
1.8–4.4 1 1.5 11 1.2 [69][58]
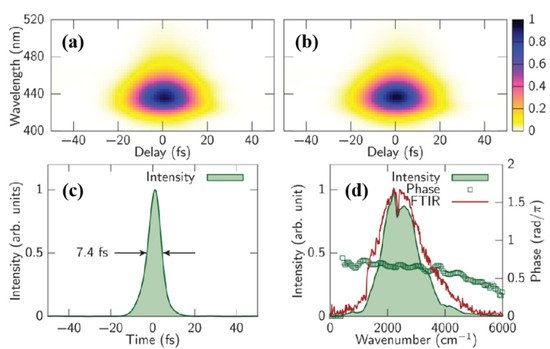
FWM 2–20 1 0.25 7.4 0.57 [70][59]
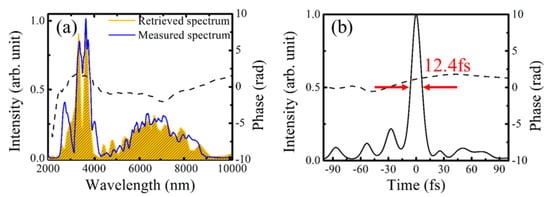
OPA 2.5–9 1 33 12.4 0.88 [35][27]
IPDFG 4–12 1 × 105 2.5 × 10−6 − − [24]
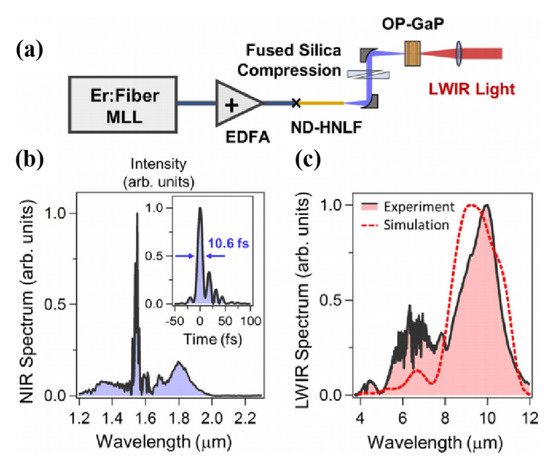
6–18 5 × 104 0.01 43 1.16 [71][60]
Pump

(μm)		 Wavelength

(μm)		 Pulse Energy

(μJ)		 Repetition Rate

(kHz)		 Power

(mW)		 Pulse Width

(fs)		 Optical Cycle Reference
1 7.6–11.5 0.59 100 59 126 3.8 [33][25]
1 5–11 0.22 50 11 32 1.2 [34][26]
2 2.5–9 33 1 33 12.4 0.88 [35][27]
2 4.2–16 3.4 1 3.4 19 0.64 [36][28]
2.4 3–10 130 1 130

4.1. MIR Single-Cycle Pulse Generation via DFG

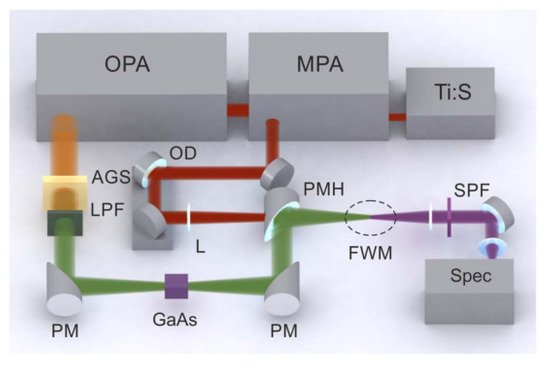
In 2015, A. A. Lanin et al. presented a MIR transient centered at a wavelength of 7.9 µm with the pulse width of 45 fs (~1.2 cycle) and the spectrum ranged from 3–18 µm at 1 kHz repetition rate [68][57]. As shown in Figure 215, first, a seed produced by supercontinuum in a sapphire plate, which was driven by 810 nm, 0.8 mJ, 65 fs, 1 kHz pulses delivered by a Ti:sappire laser. This seed was sent to an OPA with a BBO crystal, generating tunable signal and idler pulses that ranged from 1150–1580 nm and 1620–2300 nm, respectively. In the second step, the signal and idler from the OPA were used for DFG in an AGS crystal, producing a MIR pulse with a pulse duration of 150 fs and pulse energy of ~2 µJ at the central wavelength of 7.9 µm. After that, the MIR radiation underwent spectral broadening and self-compression in a 5 mm GaAs plate with high nonlinearity, leading to a spectrum covering 3–18 µm, and the pulse width compressed into 45 fs.

Photonics 08 00290 g021 550
Figure 215. Experimental setup. Ti:S, mode-locked Ti:sapphire master oscillator; MPA, multipass amplifier; OPA, optical parametric amplifier; AGS, AgGaS2 crystal; LPF, longpass filter; PM, parabolic mirror; L, BK7 glass lens; OD, optical delay line; PMH, parabolic mirror with a hole; FWM, four-wave mixing in a gas medium; SPF, shortpass filter; Spec, spectrometer. Reprinted with permission from [68][57].

4.2. MIR Single-Cycle Pulse Generation via FWM

In 2012, Y. Nomura et al. investigated MIR sub-cycle pulse generation via FWM. The fundamental mode and second-harmonic pulses of a 25 fs Ti:sappire amplifier output with the wavelength of 800 nm and energy of 0.9 mJ at 1 kHz were focused into argon gas, producing a phase-stable sub-cycle MIR pulse through FWM assisted by filament [70][59]. As shown in Figure 236, a phase-stable 250 nJ, 7.4 fs (0.57 cycles) MIR conical emission centered at 3.9 µm with its spectrum coverage of 2–20 µm was created.
Photonics 08 00290 g023 550
Figure 236. (a) Experimental and (b) retrieved XFROG traces. The retrieved pulse in (c) time and (d) frequency domain. The spectrum measured with Fourier transform spectrometer (brown solid curve) is also shown. Reprinted with permission from [70][59].

4.3. MIR Single-Cycle Pulse Generation via OPA

In 2017, H. K. Liang et al. generated a MIR sub-cycle pulse from an OPA with the signal and idler pulses at 3.2 µm and 6.4 µm [35][27]. It was demonstrated that with the stable carrier-envelope phase for both the signal and idler pulses and the careful control of the relative delay, the signal and idler pulses were synthesized without extra coherent control. As shown in Figure 247, the synthesized pulse had a spectral coverage from 2.5 to 9.0 µm, and a pulse width of 12.4 fs which corresponded to 0.88 cycles for a central wavelength of 4.2 µm.
Photonics 08 00290 g024 550
Figure 247. Temporal characterisation of the synthesised MIR pulse. The retrieved spectral (a) and temporal (b) intensity profiles of the synthesised pulse. The dotted curves are the retrieved phase. Pulse width (12.4 fs) at full width at half maximum is measured with a centre wavelength at 4.2 µm. It corresponds to 0.88 optical cycle. Reprinted with permission from [35][27].

4.4. MIR Single-Cycle Pulse Generation via IPDFG

In 2018, H. Timmers et al. presented a scheme for generating super-octave spanning MIR frequency combs with a bandwidth spanning from 4 to 12 µm through IPDFG in an OP-GaP crystal driven by a few-cycle Er-pump infrastructure [28][61]. As shown in Figure 258a, the output of an Er mode-locked laser was amplified using an Er-doped fiber amplifier. The amplified pulses then undergo nonlinear broadening in a nonlinear fiber and were compressed to a few-cycle pulse width serving as the pump of IPDFG. MIR radiation spanning from 4 to 12 µm was generated from an OP-GaP crystal. Subsequently, in 2019, from the same group, A. S. Kowligy et al. measured the temporal profile of the MIR pulse via electro-optical sampling using an ultra-short near-infrared reference pulse. A 1.2-cycle MIR pulse oscillating at a 7.6 µm centre wavelength was obtained [73][62].
Photonics 08 00290 g025 550
Figure 258. (a) Experimental layout for IPDFG comb generation. (b) The spectrum of this few-cycle driver. The inset of (b) displays the measured intensity profile of the pump pulse, corresponding to a pulse duration of 10.6 fs. (c) Super-octave longwave infrared (LWIR) spectra containing up to 0.25 mW of power. Reprinted with permission from [24].

5. Prospects of High-Power Broad-Band Few-Cycle MIR Lasers

The development of high-power broadband few-cycle MIR lasers has been driven by a number of applications in the field of strong-field physics, high-fidelity molecule detection, and cold tissue ablation applications. In strong-field physics, high-order harmonic generation (HHG) with excellent spatial coherence is probably one of the biggest driving forces of strong MIR OPCPA. Extreme ultra-violet harmonics with the photon energy exceeding the water absorption window have been generated via the MIR OPCPA pump [17]. The famous 3.9 µm OPCPA has enabled the generation of soft X-ray HHG with the photon energy extended to 1500 eV. Besides HHG, femtosecond hard X-ray covering tens of keV photon energy has been excited through plasma generation in a metallic target, pumped by the MIR OPCPA [13]. Attosecond pulse generation is another main application of MIR OPCPA in the field of strong-field physics. A total of 40–50 as isolated attosecond pulses have been generated pumped by 1.8 μm OPCPA/OPA [1]. Moreover, terahertz generation with a high conversion efficiency of 2.36% has been achieved via MIR two-colour filamentation in air pumped by MIR OPCPA centred at 3.9 µm. Besides the peak power of the MIR OPCPA system, which sets the threshold and cut-off of the aforementioned strong-field applications, the average power is another important parameter to pursue, which accounts for photon flux. Therefore, it is suggested high-average power MIR OPCPAs with decent pulse energy be the next research phase focus serving as the enablers to reveal a more uncharted continent in the field of strong-field physics.

Molecule detection is another important application of MIR OPCPA. Laser filamentation in air pumped by energetic MIR OPCPAs has been realized at the 3.9 and 2 µm wavelengths [74,75][63][64]. Stand-off detection of ambient air molecules such as CO2 have been demonstrated via air filamentation pumped using MIR OPCPA [22]. By using the atmospheric transparent windows in the MIR wavelength region, namely the 2–5.5 µm and 8–14 µm bands, more molecules in the air could be detected with MIR OPCPAs, especially at longer wavelengths such as 5 and 9 µm. In addition, dual-frequency combs (DFCs) based on broadband MIR lasers have been developed for sensitive and precision molecule sensing. With DFCs at the 3–5 µm wavelength range, the detection of molecular species in a gas mixture, including isotopologues containing isotopes such as 13C, 18O, 17O, 15N, 34S, 33S, and deuterium, with part-per-billion sensitivity and sub-Doppler resolution has been demonstrated [23]. At longer wavelengths covering 4 to 12 µm, DFCs have enabled the high-precision vapor detection of methanol and ethanol. With the high-average power of the MIR broadband laser sources at a 100 MHz repetition rate, a good signal-to-noise ratio (67 Hz1/2) has been achieved with a sub-ms acquisition time.

Besides strong-field physics and spectroscopic applications, high-power, broadband, few-cycle lasers have also been used in minimally invasive surgery. However, limited by the available femtosecond laser wavelengths, its current applications in bio-medical micro processing/surgery are only limited to cataract surgery [76,77][65][66] and myopia correction surgery [78,79,80][67][68][69]. An MIR wavelength at 3–10 µm coincides with strong molecular resonant peaks, which results in strong and sharp absorption peaks for various molecules. The strong absorption resonances of water, protein, and lipids have been investigated using MIR femtosecond laser exposure from a free-electron laser facility in ocular, brain, and dermis tissues. A new mechanism for tissue ablation was proposed. It was found that when a MIR femtosecond laser at the 6.2–6.7 µm wavelength is chosen, the laser output power is absorbed by both water and proteins. Reaching ~60 °C, collagen undergoes structural transitions from highly ordered arrays to amorphous gelatin with less resilience, which enables better tissue ablation efficiency and less lateral damages. With the emerging and development of high-power MIR femtosecond lasers at more flexible wavelengths, we foresee promising prospects for watt-level MIR femtosecond lasers in the soft and hard tissue cold ablation applications.

References

  1. Li, J.; Ren, X.; Yin, Y.; Zhao, K.; Chew, A.; Cheng, Y.; Cunningham, E.; Wang, Y.; Hu, S.; Wu, Y.; et al. 53-attosecond X-ray pulses reach the carbon K-edge. Nat. Commun. 2017, 8, 186.
  2. Popmintchev, T.; Chen, M.; Popmintchev, D.; Arpin, P.; Brown, S.; Ališauskas, S.; Andriukaitis, G.; Balčiunas, T.; Mücke, O.D.; Pugzlys, A.; et al. Bright coherent ultrahigh harmonics in the keV X-ray regime from mid-infrared femtosecond lasers. Science 2012, 336, 1287–1291.
  3. Wolter, B.; Pullen, M.G.; Le, A.-T.; Baudisch, M.; Doblhoff-Dier, K.; Senftleben, A.; Hemmer, M.; Schröter, C.D.; Ullrich, J.; Pfeifer, T.; et al. Ultrafast electron diffraction imaging of bond breaking in di-ionized acetylene. Science 2016, 354, 308–312.
  4. Colosimo, P.; Doumy, G.; Blaga, C.I.; Wheeler, J.; Hauri, C.; Catoire, F.; Tate, J.; Chirla, R.; March, A.M.; Paulus, G.G.; et al. Scaling strong-field interactions towards the classical limit. Nat. Phys. 2008, 4, 386–389.
  5. Herink, G.; Solli, D.R.; Gulde, M.; Ropers, C. Field-driven photoemission from nanostructures quenches the quiver motion. Nature 2012, 483, 190–193.
  6. Hohenleutner, M.; Langer, F.; Schubert, O.; Knorr, M.; Huttner, U.; Koch, S.W.; Kira, M.; Huber, R. Real-time observation of interfering crystal electrons in high-harmonic generation. Nature 2015, 523, 572–575.
  7. Ghimire, S.; DiChiara, A.D.; Sistrunk, E.; Agostini, P.; DiMauro, L.F.; Reis, D.A. Observation of high-order harmonic generation in a bulk crystal. Nat. Phys. 2011, 7, 138–141.
  8. Schubert, O.; Hohenleutner, M.; Langer, F.; Urbanek, B.; Lange, C.; Huttner, U.; Golde, D.; Meier, T.; Kira, M.; Koch, S.W.; et al. Sub-cycle control of terahertz high-harmonic generation by dynamical Bloch oscillations. Nat. Photonics 2014, 8, 119–123.
  9. Rybka, T.; Ludwig, M.; Schmalz, M.F.; Knittel, V.; Brida, D.; Leitenstorfer, A. Sub-cycle optical phase control of nanotunnelling in the single-electron regime. Nat. Photonics 2016, 10, 667–670.
  10. Schliesser, A.; Picqué, N.; Hänsch, T.W. Mid-infrared frequency combs. Nat. Photonics 2012, 6, 440–449.
  11. Haas, J.; Mizaikoff, B. Advances in mid-infrared spectroscopy for chemical analysis. Annu. Rev. Anal. Chem. 2016, 9, 45–68.
  12. Kara, O.; Maidment, L.; Gardiner, T.; Schunemann, P.G.; Reid, D.T. Dual-comb spectroscopy in the spectral fingerprint region using OPGaP optical parametric oscillators. Opt. Express 2017, 25, 32713–32721.
  13. Keilmann, F.; Gohle, C.; Holzwarth, R. Time-domain mid-infrared frequency-comb spectrometer. Opt. Lett. 2004, 29, 1542–1544.
  14. Schmidt, C.; Pertot, Y.; Balciunas, T.; Zinchenko, K.; Matthews, M.; Wörner, H.J.; Wolf, J.-P. High-order harmonic source spanning up to the oxygen K-edge based on filamentation pulse compression. Opt. Express 2018, 26, 11834–11842.
  15. Teichmann, S.M.; Silva, F.; Cousin, S.L.; Hemmer, M.; Biegert, J. 0.5-keV Soft X-ray attosecond continua. Nat. Commun. 2016, 7, 11493.
  16. Popmintchev, D.; Galloway, B.R.; Chen, M.; Dollar, F.; Mancuso, C.A.; Hankla, A.; Miaja-Avila, L.; O’Neil, G.; Shaw, J.M.; Fan, G.; et al. Near- and extended-edge X-ray-absorption fine-structure spectroscopy using ultrafast coherent high-order harmonic supercontinua. Phys. Rev. Lett. 2018, 120, 093002.
  17. Weisshaupt, J.; Juvé, V.; Holtz, M.; Ku, S.; Woerner, M.; Elsaesser, T.; Ališauskas, S.; Pugžlys, A.; Baltuška, A. High-brightness table-top hard X-ray source driven by sub-100-femtosecond mid-infrared pulses. Nat. Photonics 2014, 8, 927–930.
  18. Gaumnitz, T.; Jain, A.; Pertot, Y.; Huppert, M.; Jordan, I.; Ardana-Lamas, F.; Wörner, H.J. Streaking of 43-attosecond soft-X-ray pulses generated by a passively CEP-stable mid-infrared driver. Opt. Express 2017, 25, 27506–27518.
  19. Koulouklidis, A.D.; Gollner, C.; Shumakova, V.; Fedorov, V.Y.; Pugžlys, A.; Baltuška, A.; Tzortzakis, S. Observation of extremely efficient terahertz generation from mid-infrared two-color laser filaments. Nat. Commun. 2020, 11, 292.
  20. Manceau, J.-M.; Loukakos, P.A.; Tzortzakis, S. Direct acoustic phonon excitation by intense and ultrashort terahertz pulses. Appl. Phys. Lett. 2010, 97, 251904.
  21. Mitrofanov, A.V.; Sidorov-Biryukov, D.A.; Nazarov, M.M.; Voronin, A.A.; Rozhko, M.V.; Shutov, A.D.; Serebryannikov, E.E.; Fedotov, A.B.; Zheltikov, A.M. Ultraviolet-to-millimeter-band supercontinua driven by ultrashort mid-infrared laser pulses. Optica 2020, 7, 15–19.
  22. Ycas, G.; Giorgetta, F.R.; Baumann, E.; Coddington, I.; Herman, D.; Diddams, S.A.; Newbury, N.R. High-coherence mid-infrared dual-comb spectroscopy spanning 2.6 to 5.2 μm. Nat. Photonics 2018, 12, 202–208.
  23. Muraviev, A.V.; Smolski, V.O.; Loparo, Z.E.; Vodopyanov, K.L. Massively parallel sensing of trace molecules and their isotopologues with broadband subharmonic mid-infrared frequency combs. Nat. Photonics 2018, 12, 209–214.
  24. Timmers, H.; Kowligy, A.; Lind, A.; Cruz, C.F.; Nader, N.; Silfies, M.; Ycas, G.; Allison, T.K.; Schunemann, P.G.; Papp, S.B.; et al. Molecular fingerprinting with bright, broadband infrared frequency combs. Optica 2018, 5, 727–732.
  25. Heiner, Z.; Petrov, V.; Mero, M. Efficient, sub-4-cycle, 1-µm-pumped optical parametric amplifier at 10 µm based on BaGa4S7. Opt. Lett. 2020, 45, 5692–5695.
  26. Chen, B.; Wittmann, E.; Morimoto, Y.; Baum, P.; Riedle, E. Octave-spanning single-cycle middle-infrared generation through optical parametric amplification in LiGaS2. Opt. Express 2019, 27, 21306–21318.
  27. Liang, H.; Krogen, P.; Wang, Z.; Park, H.; Kroh, T.; Zawilski, K.; Schunemann, P.; Moses, J.; Dimauro, L.; Kartner, F.X.; et al. High-energy mid-infrared sub-cycle pulse synthesis from a parametric amplifier. Nat. Commun. 2017, 8, 141.
  28. Liu, K.; Liang, H.; Wang, L.; Qu, S.; Lang, T.; Li, H.; Wang, Q.J.; Zhang, Y. Multimicrojoule GaSe-based midinfrared optical parametric amplifier with an ultrabroad idler spectrum covering 4.2–16 µm. Opt. Lett. 2019, 44, 1003–1006.
  29. Nam, S.-H.; Fedorov, V.; Mirov, S.; Hong, K.-H. Octave-spanning mid-infrared femtosecond OPA in a ZnGeP2 pumped by a 2.4 µm Cr:ZnSe chirped-pulse amplifier. Opt. Express 2020, 28, 32403–32414.
  30. Deng, Y.; Schwarz, A.; Fattahi, H.; Ueffing, M.; Gu, X.; Ossiander, M.; Metzger, T.; Pervak, V.; Ishizuki, H.; Taira, T.; et al. Carrier-envelope-phase-stable, 1.2 mJ, 1.5 cycle laser pulses at 2.1 µm. Opt. Lett. 2012, 37, 4973–4975.
  31. Feng, T.; Heilmann, A.; Bock, M.; Ehrentraut, L.; Witting, T.; Yu, H.; Stiel, H.; Eisebitt, S.; Schnürer, M. 27 W 2.1 µm OPCPA system for coherent soft X-ray generation operating at 10 kHz. Opt. Express 2020, 28, 8724–8733.
  32. Lai, C.; Hong, K.; NSiqueira, J.P.; Krogen, P.; Chang, C.; Stein, G.J.; Liang, H.; Keathley, P.D.; Laurent, G.; Moses, J. Multi-mJ mid-infrared kHz OPCPA and Yb-doped pump lasers for tabletop coherent soft x-ray generation. J. Opt. 2015, 17, 094009.
  33. Pupeikis, J.; Chevreuil, P.-A.; Bigler, N.; Phillips, C.R.; Keller, U. Water window soft x-ray source enabled by a 25 W few-cycle 2.2 µm OPCPA at 100 kHz. Optica 2020, 7, 168–171.
  34. Bigler, N.; Pupeikis, J.; Hrisafov, S.; Gallmann, L.; Phillips, C.R.; Keller, U. High-power OPCPA generating 1.7 cycle pulses at 2.5 µm. Opt. Express 2018, 26, 26750–26757.
  35. Zou, X.; Li, W.; Liang, H.; Liu, K.; Qu, S.; Wang, Q.J.; Zhang, Y. 300 µJ, 3 W, few-cycle, 3 µm OPCPA based on periodically poled stoichiometric lithium tantalate crystals. Opt. Lett. 2019, 44, 2791–2794.
  36. Zou, X.; Li, W.; Qu, S.; Liu, K.; Li, H.; Wang, Q.J.; Zhang, Y.; Liang, H. Flat-top pumped multi-millijoule mid-infrared parametric chirped-pulse amplifier at 10 kHz repetition rate. Laser Photonics Rev. 2021, 15, 2000292.
  37. Rigaud, P.; Walle, A.V.; Hanna, M.; Forget, N.; Guichard, F.; Zaouter, Y.; Guesmi, K.; Druon, F.; Georges, P. Supercontinuum-seeded few-cycle mid-infrared OPCPA system. Opt. Express 2016, 24, 26494–26502.
  38. Mero, M.; Heiner, Z.; Petrov, V.; Rottke, H.; Branchi, F.; Thomas, G.M.; Vrakking, M.J.J. 43 W, 1.55 µm and 12.5 W, 3.1 µm dual-beam, sub-10 cycle, 100 kHz optical parametric chirped pulse amplifier. Opt. Lett. 2018, 43, 5246–5249.
  39. Thiré, N.; Maksimenka, R.; Kiss, B.; Ferchaud, C.; Gitzinger, G.; Pinoteau, T.; Jousselin, H.; Jarosch, S.; Bizouard, P.; Piero, V.D.; et al. Highly stable, 15 W, few-cycle, 65 mrad CEP noise mid-IR OPCPA for statistical physics. Opt. Express 2018, 26, 26907–26915.
  40. Elu, U.; Baudisch, M.; Pires, H.; Tani, F.; Frosz, M.H.; Köttig, F.; Ermolov, A.; Russell, P.S.J.; Biegert, J. High average power and single-cycle pulses from a mid-IR optical parametric chirped pulse amplifier. Optica 2017, 4, 1024–1029.
  41. Mayer, B.W.; Phillips, C.R.; Gallmann, L.; Fejer, M.M.; Keller, U. Sub-four-cycle laser pulses directly from a high-repetition-rate optical parametric chirped-pulse amplifier at 3.4 μm. Opt. Lett. 2013, 38, 4265–4268.
  42. Zhao, K.; Zhong, H.; Yuan, P.; Xie, G.; Wang, J.; Ma, J.; Qian, L. Generation of 120 GW mid-infrared pulses from a widely tunable noncollinear optical parametric amplifier. Opt. Lett. 2013, 38, 2159–2161.
  43. Andriukaitis, G.; Balčiūnas, T.; Ališauskas, S.; Pugžlys, A.; Baltuška, A.; Popmintchev, T.; Chen, M.-C.; Murnane, M.M.; Kapteyn, H.C. 90 GW peak power few-cycle mid-infrared pulses from an optical parametric amplifier. Opt. Lett. 2011, 36, 2755–2757.
  44. Wang, P.; Li, Y.; Li, W.; Su, H.; Shao, B.; Li, S.; Wang, C.; Wang, D.; Zhao, R.; Peng, Y.; et al. 2.6 mJ/100 Hz CEP-stable near-single-cycle 4 µm laser based on OPCPA and hollow-core fiber compression. Opt. Lett. 2018, 43, 2197–2200.
  45. Grafenstein, L.V.; Bock, M.; Ueberschaer, D.; Escoto, E.; Koç, A.; Zawilski, K.; Schunemann, P.; Griebner, U.; Elsaesser, T. Multi-millijoule, few-cycle 5 µm OPCPA at 1 kHz repetition rate. Opt. Lett. 2020, 45, 5998–6001.
  46. Elu, U.; Steinle, T.; Sanchez, D.; Maidment, L.; Zawilski, K.; Schunemann, P.; Zeitner, U.D.; Simon-Boisson, C.; Biegert, J. Table-top high-energy 7 µm OPCPA and 260 mJ Ho:YLF pump laser. Opt. Lett. 2019, 44, 3194–3197.
  47. Qu, S.; Liang, H.; Liu, K.; Zou, X.; Li, W.; Wang, Q.J.; Zhang, Y. 9 µm few-cycle optical parametric chirped-pulse amplifier based on LiGaS2. Opt. Lett. 2019, 44, 2422–2425.
  48. Chen, B.-H.; Nagy, T.; Baum, P. Efficient middle-infrared generation in LiGaS2 by simultaneous spectral broadening and difference-frequency generation. Opt. Lett. 2018, 43, 1742–1745.
  49. Pupeza, I.; Sánchez, D.; Zhang, J.; Lilienfein, N.; Seidel, M.; Karpowicz, N.; Paasch-Colberg, T.; Znakovskaya, I.; Pescher, M.; Schweinberger, W.; et al. High-power sub-two-cycle mid-infrared pulses at 100 MHz repetition rate. Nat. Photonics 2015, 9, 721–724.
  50. Gaida, C.; Gebhardt, M.; Heuermann, T.; Stutzki, F.; Jauregui, C.; Antonio-Lope, J.; Schulzgen, A.; Amezcua-Correa, R.; Tunnermann, A.; Pupeza, L.; et al. Watt-scale super-octave mid-infrared intrapulse difference frequency generation. Light Sci. Appl. 2018, 7, 94.
  51. Zhang, J.; Fritsch, K.; Wang, Q.; Krause, F.; Mak, K.F.; Pronin, O. Intra-pulse difference-frequency generation of mid-infrared (2.7–20 µm) by random quasi-phase-matching. Opt. Lett. 2019, 44, 2986–2989.
  52. Zhang, J.; Mak, K.F.; Nagl, N.; Seidel, M.; Bauer, D.; Sutter, D.; Pervak, V.; Krausz, F.; Pronin, O. Multi-mW, few-cycle mid-infrared continuum spanning from 500 to 2250 cm–1. Light Sci. Appl. 2018, 7, 17180.
  53. Novak, O.; Krogen, P.R.; Kroh, T.; Mocek, T.; Kartner, F.X.; Hong, K.-H. Femtosecond 8.5 µm source based on intrapulse difference-frequency generation of 2.1 µm pulses. Opt. Lett. 2018, 43, 1335–1338.
  54. Vasilyev, S.; Moskalev, I.S.; Smolski, V.O.; Peppers, J.M.; Mirov, M.; Muraviev, A.V.; Zawilski, K.; Schunemann, P.G.; Mirov, S.B.; Vodopyanov, K.L.; et al. Super-octave longwave mid-infrared coherent transients produced by optical rectification of few-cycle 2.5-μm pulses. Optica 2019, 6, 111–114.
  55. Liu, K.; Liang, H.; Qu, S.; Li, W.; Zou, X.; Zhang, Y.; Wang, Q.J. High-energy mid-infrared intrapulse difference-frequency generation with 5.3% conversion efficiency driven at 3 µm. Opt. Express 2019, 27, 37706–37713.
  56. Junginger, F.; Sell, A.; Schubert, O.; Mayer, B.; Brida, D.; Marangoni, M.; Cerullo, G.; Leitenstorfer, A.; Huber, R. Single-cycle multiterahertz transients with peak fields above 10 MV/cm. Opt. Lett. 2010, 35, 2645–2647.
  57. Lanin, A.A.; Voronin, A.A.; Stepanov, E.A.; Fedotov, A.B.; Zheltikov, A.M. Multioctave, 3–18 µm sub-two-cycle supercontinua from self-compressing, self-focusing soliton transients in a solid. Opt. Lett. 2015, 40, 974–977.
  58. Krogen, P.; Suchowski, H.; Liang, H.; Flemens, N.; Hong, K.-H.; Kärtner, F.X.; Moses, J. Generation and multi-octave shaping of mid-infrared intense single-cycle pulses. Nat. Photon. 2017, 11, 222–226.
  59. Nomura, Y.; Shirai, H.; Ishii, K.; Tsurumachi, N.; Voronin, A.A.; Zheltikov, A.M.; Fuji, T. Phase-stable sub-cycle mid-infrared conical emission from filamentation in gases. Opt. Express 2012, 20, 24741–24747.
  60. Butler, T.P.; Gerz, D.; Hofer, C.; Xu, J.; Gaida, C.; Heuermann, T.; Gebhardt, M.; Vamos, L.; Schweinberger, W.; Gessner, J.A.; et al. Watt-scale 50-MHz source of single-cycle waveform-stable pulses in the molecular fingerprint region. Opt. Lett. 2019, 44, 1730–1733.
  61. Wandel, S.; Lin, M.; Yin, Y.; Xu, G.; Jovanovic, I. Parametric generation and characterization of femtosecond mid-infrared pulses in ZnGeP2. Opt. Express 2016, 24, 5287–5299.
  62. Kowligy, A.S.; Timmers, H.; Lind, A.J.; Elu, U.; Cruz, F.C.; Schunemann, P.G.; Biegert, J.; Diddams, S.A. Infrared electric field sampled frequency comb spectroscopy. Sci. Adv. 2019, 5, eaaw8794.
  63. Mitrofanov, A.V.; Voronin, A.A.; Sidorov-Biryukov, D.A.; Pugžlys, A.; Stepanov, E.A.; Andriukaitis, G.; Flöry, T.; Ališauskas, S.; Fedotov, A.B.; Baltuška, A.; et al. Mid-infrared laser filaments in the atmosphere. Sci. Rep. 2015, 5, 8368.
  64. Liang, H.; Weerawarne, D.L.; Krogen, P.; Grynko, R.I.; Lai, C.J.; Shim, B.; Kärtner, F.X.; Hong, K.H. Mid-infrared laser filaments in air at a kilohertz repetition rate. Optica 2016, 3, 678–681.
  65. Nagy, Z.; Takacs, A.; Filkorn, T.; Sarayba, M. Initial clinical evaluation of an intraocular femtosecond laser in cataract surgery. J. Refract. Surg. 2009, 25, 1053–1060.
  66. Taravella, M.J.; Meghpara, B.; Frank, G.; Gensheimer, W.; Davidson, R. Femtosecond laser–assisted cataract surgery in complex cases. J. Cataract Refract. Surg. 2016, 42, 813–816.
  67. Shah, R.; Shah, S. Effect of scanning patterns on the results of femtosecond laser lenticule extraction refractive surgery. J. Cataract Refract. Surg. 2011, 37, 1636–1647.
  68. Sekundo, W.; Kunert, K.; Russmann, C.; Gille, A.; Bissmann, W.; Stobrawa, G.; Sticker, M.; Bischoff, M.; Blum, M. First efficacy and safety study of femtosecond lenticule extraction for the correction of myopia: Six-month results. J. Cataract Refract. Surg. 2008, 34, 1513–1520.
  69. Blum, M.; Kunert, K.; Schröder, M.; Sekundo, W. Femtosecond lenticule extraction for the correction of myopia: Preliminary 6-month results. Graefes Arch. Clin. Exp. Ophthalmol. 2010, 248, 1019–1027.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/)
ScholarVision Creations
Feedback