Recent evidence suggests that a broad range of complex and dynamic processes in living systems could exploit quantum effects to enhance and/or regulate biological functions. These non-trivial quantum effects may play a crucial role in maintaining the non-equilibrium state of biomolecular systems so as to achieve biological advantages that cannot be understood within the boundaries of classical physics. Quantum biology is the study of such quantum aspects of living systems.
- quantum biology
- non-trivial quantum effects in biology
- quantum tunnelling in enzyme-catalysed reactions
- photosynthesis
- synthetic light harvesting system
- ion channel
- fluorescent protein
- magnetoreception
- radical pairs
- proton tunnelling in DNA
1. Introduction
Biology has traditionally been considered to belong to the classical domain, while physics and chemistry are deeply entrenched in quantum mechanics. Yet, living systems are fundamentally quantum mechanical since the dynamics of their molecular, atomic and sub-atomic chemical machinery is, like everything else, governed by the law of quantum physics. Does this atomic scale matter in biology? Does life need quantum mechanics? In other words, can quantum mechanics play a fundamental role and have a physiological impact in biology? Most importantly, are there any biological molecules or biomolecular systems that exploit non-trivial quantum mechanical effects to achieve biological advantages that cannot be understood within the boundaries of classical physics? Many of the early pioneers of quantum mechanics thought that the answer to this question was an affirmative yes [1], as most famously argued by Erwin Schrödinger’s highly influential book “What is Life?” [2].
Yet, until recently, most approaches to investigate quantum effects in biology, like Schrödinger’s, were entirely theoretical. This was largely because experimental approaches capable of detecting delicate and fragile quantum effects in biological systems that were dominated by random molecular interactions had not been developed yet. However, at this stage, it is useful to define what we mean by “quantum effects” in quantum biology. As already pointed out, at its most fundamental level of particles, atoms and molecules, biology, life, like everything in the world, is governed by quantum laws. For example, the structure of electronic orbitals and chemical bonds, what are sometimes referred to as examples of “trivial quantum mechanics”, are as central to structural biology as they are to chemistry or physics; yet structural biology is not usually considered to be a branch of quantum biology. What is meant by quantum biology is the involvement of phenomena that are normally confined to the quantum realm of atoms and molecules, such as coherence, tunnelling, entanglement or spin, because their effects are normally cancelled out at the macroscopic level due to decoherence [2] and would thereby be thought highly improbable inside the warm, wet and disordered environments inside living cells. More importantly, to be non-trivial, such effects must explain or drive a biological process that is likely optimised by evolution. That is, for a quantum effect to be non-trivial, biology must have evolved to exploit it [3]. In contrast, a trivial quantum effect may be detected but just arises from the material being made of atoms, molecules, electrons, etc—all of which are described by quantum mechanics.
2. Quantum Effects in Photosynthesis
Photosynthetic organisms harvest light using networks of chromophores that absorb the light and efficiently funnel solar energy toward a reaction centre where charge separation occurs. Nature’s complex system of chromophores form an antenna to harvest light, separating the light harvesting from the charge separation—a design principle that researchers would like to copy in next-generation technologies. Photosynthetic growth occurs via the conversion of molecular excitations into long-lived chemical energy in the form of adenosine triphosphate (ATP) and reduced nicotinamide adenine dinucleotide phosphate. These energy-rich molecules fuel the fixation of CO2 via the Calvin–Benson–Bassham cycle [4]. The overall process of photosynthesis is fairly thermodynamically inefficient, with a practical maximal efficiency of light to biomass conversion of below 10% [5][6]. However, the initial step of capturing a photon with a light-harvesting molecule and the transportation to a reaction centre happens with a quantum efficiency of near unity. At the same time, these processes are remarkably robust [7]. This highly evolved process has been proposed to take advantage of quantum mechanical effects, despite the warm and noisy environment in which photosynthesis operates [8]. Understanding the mechanisms operative within the light-harvesting antenna and subsequent transport to the reaction centre within the photosynthetic organism may help to define the next-generation of green energy solutions and optoelectronics.
2.1. Theory and Experimental Studies
Quantum dynamics has been proposed to play an important role in the light reactions of photosynthesis and these ideas, though contentious, have received support from both theoretical and experimental studies. Photosynthesis light-harvesting complexes generally consist of extended arrays of pigments fixed to a rigid protein scaffold. The dense packing of chromophores leads to a range of interactions and coupling strengths within each complex. After absorption of photons by a pigment (or group of pigments) contained within a given light harvesting complex (LHC), the transfer of energy occurs among these molecules. For chromophores with large separations and a low Coulombic interaction, Förster resonance energy transfer (FRET) theory [9] provides an accurate description of the energy transfer as a series of “incoherent hops.” For strongly coupled chromophores with relatively weak coupling to their surroundings, Redfield theory provides a good description of energy transfer as relaxation within the coupled chromophores. More complex descriptions are needed when multiple types of couplings are relatively strong or where specific motions within the bath are important. Regardless of mechanism, energy is ultimately trapped into a reaction centre (RC), where charge separation takes place. In a bacterial system, electronic transitions are guided by a “downhill energy funnel” from higher energy states to lower energy states, but in higher plants, such energy separation is not obvious.
The description of energy transfer in photosynthesis has a very long history from coherent descriptions in 1932 by Perrin [10] to Förster’s seminal work in 1945 [11]. However, it has become clear that FRET alone cannot be employed to explain the process occurring in photosynthesis due to a significant coupling strength outside of the FRET regime between their photoexcited chromophores [12][13][14][15][16][17]. Moreover, random energy transfer between densely packed antennae pigments would lead to high losses to the environment before reaching the RC, resulting in a lower photosynthetic quantum yield than observed [18][19][20]. Highly packed pigments, e.g., in the light-harvesting complex 2 of purple bacteria (LH2), demonstrate stronger couplings and interaction strengths occurring between molecules wherein the excitation is not isolated to a specific pigment, but rather delocalised in the form of a Frenkel exciton [21][22]. Given the wide range of structures seen in the natural world, it is not surprising that the Redfield and Förster models that describe strongly coupled and weakly coupled regimes respectively are inadequate to describe the coupling of all chromophores within photosynthetic complexes [13]. Many systems appear to occupy an intermediate regime that is not captured well by theories describing either extreme of coupling strength [23]. Modified versions of these models have been built to account for several important phenomena seen during experimental observations [24][25][26]. For specific mathematical models of the bath surrounding the chromophores, the problem has been solved exactly by Ishizaki and Tanimura using hierarchical equations of motion [27][28]. A more general pseudomode method has been introduced by Lambert and co-workers that includes Matsubara terms and is readily suited for low temperature studies [29]. Other exact methods for arbitrary harmonic bath models have been introduced by Plenio and co-workers exploiting density matrix renormalisation group methods [30][31][32][33].
With the advance in new spectroscopic techniques such as two-dimensional electronic spectroscopy (2DES), phase-sensitive investigations into the nature of the energy transfer taking place in LHCs could be performed. An accessible introduction to the theory and data analysis of 2DES signals are provided by Gelzinis et al. and Wang et al. [34][35] In short, contrasting with the classical pump-probe spectroscopy, in 2DES the excitation frequency is resolved, permitting more accurate maps of energy transfer in spectral congested systems. After the excitation of the absorption electronic bands of a given system (recorded on the excitation axis, ωexcite), the system evolves during a waiting time (t2 or tdelay) having its current state recorded on a detection axis (ωdetect) to generate a correlation map. On this map, diagonal peaks correspond roughly to the linear spectrum of the system and the cross-peaks to the interactions occurring between their absorption bands, arising early (transitions occurring between common electronic orbitals) or later (energy transfer) and possibly oscillating with the time (Figure 1A). In this way, this technique has been successfully employed during the last decades for obtaining information on energy transfer pathways, interactions occurring between the system and the surrounding environment (bath) [36][37].
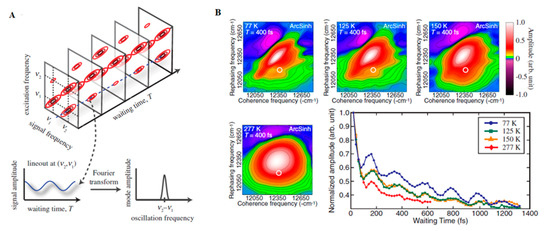
Figure 1. (A) Time Evolution of signal amplitudes obtained with 2DES. A cross-peak is shown oscillating in the frequency equivalent to the energy difference between the two states in the diagonal. A Fourier transformation is the applied to extract the frequency of the beating signal. Adapted from ref. [22] (B) 2DES spectra obtained for the FMO complex at different temperatures at Tdelay = 400 fs. The oscillations obtained for a given spectral position (white circle) possess a similar phase and frequency in all cases with shorter lifetimes at physiological temperatures (277 K). Adapted from ref. [38]
Energy levels found within a photosynthetic complex are thought to be tuned to the environmental bath composed of protein and solvent interactions [39]. However there is some debate over where the line between system and bath is drawn [40]. As progress in the field continues, we see how the system now encompasses more of what was typically previously seen as the bath dynamics. The tuning of spectral properties of the pigments due to their coupling, as well as with the protein and solvent environment facilitates ultrafast energy transfer, interactions between chromophores and many other aspects related to the temporal dynamics of LHCs.
The application of 2DES at cryogenic temperature (77K) to track energy transport within the Fenna–Mattews–Olson (FMO) complexes of the green sulphur bacterium Chlorobium tepidum by Engel et al. in 2007 was one of the key advances of modern quantum biology as it provided evidence for the possible involvement of quantum dynamics occurring within this system [41]. In this work, oscillating cross-peaks arising at early waiting times up to 660 fs were attributed to electronic coherences occurring between the chromophores enclosed within the protein. These ultrafast “quantum beats” witness the rapidly changing populations of excited states within the system. The occurrence of strong coupling between Frenkel excitons formed after the light absorption and the consequent delocalization of their excitation, is by itself a quantum effect capable of modifying energy transfer pathways occurring within light-harvesting complexes, due to modifications of their collective dipole configurations. However, it is possible that quantum mechanics are playing an even bigger role in the process, by allowing the system to sample different pathways simultaneously through the superposition of states and finding the most efficient path to the reaction centre, constituting what researchers have been calling a “quantum walk.” Quantum entanglement has also been proposed to be playing a role in the system [42], although this is more conjectural.
The landmark paper by Engel et al. [41] received many critics from specialists in the field, which argued that the oscillations observed in the work should be attributed vibrational modes on the electronic ground state of the protein system [43]. Nevertheless, it also provoked a flurry of similar studies investigating the concept of long-lived coherence in photosynthesis. Most studies have focused on the light harvesting complexes of purple non-sulfur (LH1-RC and LH2) and green-sulfur (FMO) bacteria. For example, in 2007, Lee et al. used two colour electronic coherence photon echo spectroscopy (2CECPE) to characterize coherences between chromophores present within the isolated reaction centres (RCs) of Rhodobacter sphaeroides [44] and similarly detected quantum beats persisting for longer than 400 fs (at 77 K). The study also provided evidence of strongly correlated and long-lived nuclear modes, suggesting than the energy levels of the chromophores were being modulated by vibrational modes. The finding that the vibrational modes were of similar frequencies to those of the excitonic energy gap suggested a vibronic scenario in which nuclear vibrations were fine-tuned to enhance electronic energy transfer [45][46]. A theoretical study of the FMO complex [47][48] came to similar conclusions. Vibronic transport has also been shown to increase the energy transfer by 10% in the LHC of the algae Chroomonas mesostigmatica [49]. The possibility of resonance between electronic and vibrational states leads to some interesting and non-trivial dynamics of mixed character that are thought to influence energy transfer in both the antennae complexes and reaction centres [47][50][51]. For additional studies of other model LHCs, we refer the reader to refs. [52][53][54].
A key question is how relevant long-lived coherences measured in the laboratory are to photosynthesis taking place within noisy biological environments [43][55][56]. However, a key concept that has emerged from several studies is the role that the environment may play in actually enhancing, rather than destroying quantum coherence. Experiments carried on the FMO complex at physiologic temperatures (277 K) demonstrated quantum beats that persisted for 300 fs (Figure 1B). A similar study of LH2 of Rhodopseudomonas acidophila 10050 demonstrated quantum beats persisting for at least 400 fs, long enough to play a non-trivial role in the energy transfer [38][57]. Another room temperature study of the LH2 of Rhodobacter sphaeroides provided evidence of a role for environment-assisted quantum interference between multiple energy transfer and relaxation pathways in a phenomenon often called quantum phonon antennae [58][59]. The findings were consistent with theoretical studies that predicted the enhancement of energy transport at intermediate noise levels, corresponding to those characteristics of room temperature, when the dephasing frequency is tuned to the excitonic energy gaps and couplings [60][61][62]. Although it has been argued that results, such as these, provide evidence of classical, rather than quantum behaviour, from his own work on the LH2 of Rhodoblastus acidophilus (formerly Rhodopseudomonas acidophila 7050), Jang argued that quantum mechanical dynamics cannot be neglected when modelling transfer dynamics between LHCs is separated by more than 1 nm. Nevertheless, the interpretation of these spectra remains controversial, with several researchers opting for an interpretation of a mixture of excitonic dynamics and FRET involved in the energy transfer [63].
While extensive quantum biology studies focus on excitation energy transfer, biology also exploits proton transfer and there are suggestions that the quantum efficiency of this mechanism may also be enhanced by quantum effects [64]. Halobacteria possess retinal-containing protein complexes called bacteriorhodopsins that function by pumping protons across their membrane upon absorption of a photon [65][66]. The light-driven proton transfer mediated by these proteins, generates a proton gradient, which drives the synthesis of ATP by ATPases localised in the membrane of these bacteria constituting an important alternative source of energy [66]. These complexes are currently being commercialised in the form of membrane patches obtained from Halobacterium salinarum and are employed during the production of artificial retina, photosensitive and erasable material for optical information, recording and processing and electronic ink for laptop display [67][68][69][70]. A simple model of light-induced proton pumps in artificial photosynthetic systems was studied by Ghosh et al. in which a photon-to-proton quantum yield of the model system was analysed as ~55% [71].
2.2. Bio-Inspired Synthetic Light Harvesting Systems
2DES experimental spectra of photosynthetic complexes can easily become congested and thereby difficult to interpret. To counteract this, investigations into energy transfer dynamics in photosynthetic complexes have recently been conducted in simpler bio-inspired synthetic systems constructed with biological and synthetic parts. Such hybrid biotic/abiotic systems are also of interest because they could provide the prototypes of next-generation green energy technologies including incorporation into solar cells [72][73]. Alongside theoretical modelling of the quantum dynamics of both charge and energy transfer in an artificial system [74], such an approach can complement lab-based investigations [75]. Design principles of lab-based bio-inspired systems typically utilise a biologically relevant chromophore system anchored to a scaffold through various covalent and non-covalent functionalizations that are designed to mimic chromophore–pigment interactions.
As described above, coupling of chromophores to their environment in a LHC is thought to play a vital role in facilitating fast energy transfer. In one study of energy transfer from carotenoid peridinin donor to acceptor chlorophylls from marine dinoflagellates [76], the energy gap between donor and acceptor was tuned to modify, and thereby investigate, the role of electronic and vibrational coupling. The data-rich technique of 2DES demonstrated that minor changes to the chlorophyll functional groups (e.g., the formyl group) led to faster decoherence and lowered energy transfer efficiency within the complex [76]. An easily modifiable scaffold, such as the tobacco mosaic virus capsid protein, offers a highly versatile base from which chromophores can be attached at precise locations using linkers of varying length and rigidities. In one study, rotationally rigid linkers were shown to have a large influence on the lifetime of exciton correlations [77].
To further investigate linker chemistry, the distinct vibrational properties of chemically functionalised carbon nanotubes was utilised to probe the effects of vibronic coupling on coherence and energy transport within various chromophore heterodimers [78]. In addition, room temperature quantum beatings associated with strong vibronic coupling was demonstrated in a system of multichromophoric synthetic heterodimers with rigid linker chemistry [79].
Dimerised chromophores provide another means to investigate variables affecting interchromophore coupling and long-range efficient charge transfer, as well as representing the reaction centre photoinduced charge separation of the special pair. Using both symmetric and anti-symmetric dyads, the extent of excitonic coupling on coherence times can be investigated without the typical experimental challenges associated with direct in vivo experiments on reaction centres and their many reaction pathways [78]. In a bio-inspired synthetic model system of bacterial photosynthesis, absorption spectra of bacteriochlorin (BC) dimers as seen in Figure 2a were measured with phenylene bridges of varying lengths [80]. Stronger dimer interaction due to the shorter phenylene bridges led to excitonic splitting of bands and faster relaxation, as seen in the time-resolved photoluminescence spectra in Figure 2b. Additionally, the excited state dynamics of the stronger coupled system was drastically modified by bridge length and solvent choice. Efficiency of charge transfer decreased with increased bridge length by nearly one order of magnitude with each phenylene addition [80]. Dynamics of the system was investigated by 2DES and was shown to be consistent with coherence having both electronic and vibrational components [81].
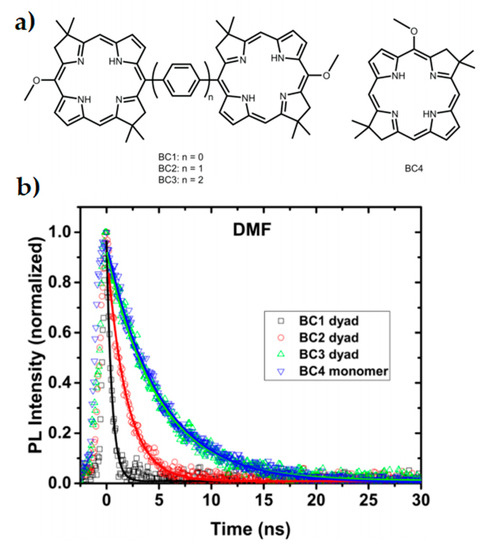
Figure 2. Inserting phenylene bridges between two chromophores shown in (a) has a profound effect on the coupling and excited state dynamics of a dimer system. Faster relaxation is seen in the time-resolved photoluminescence spectra (b) when the coupling is stronger and the pigment spacing is smaller. This study reflects properties seen within special pairs in cyanobacteria. Adapted from ref. [80].
Considerable efforts have also been invested in projects aimed at building more complex and bio-inspired wholly synthetic systems, although larger aggregates are still some way off the complexity of a biological light-harvesting complex. Drawing inspiration from biological light harvesting complexes, chlorosomal J-aggregates have been employed as a mimic of the chlorosomal light-harvesting units within green bacterial photosynthesis and exhibited efficient singlet energy transfer using a biologically relevant solvent [82][83]. Elsewhere, the rigid scaffold chromophore interactions of natural light-harvesting systems have been mimicked with cyanine dye-derived host solid-state matrix. Focusing on the structural similarities to chromosomal assemblies in green sulfur bacteria capable of low-light photosynthesis, the solid-state environment was found to modulate vibronic coupling of the system and direct energy transfer [84]. Agglomeration of dyes into nanotubes and structured bundles bio-inspired green bacteria facilitated longer exciton diffusion lengths and wider exciton delocalisation consistent with theory [85][86][87]. Using similar systems, vibronic coupling was shown to be the origin of long-lived beating signals in tubular and nanoring artificial light harvesting architectures that mimicked inter-pigment distances [88][89].
3. Fluorescent Protein as a Novel Model System for Quantum Biology
3.1. Excitation Energy Transfer
In 1965, Förster proposed three main regimes for energy transfer between donor and acceptor fluorophores that share common atomic transitions: “strong”, intermediate “weak” and “very weak” coupling [90]. This distinction is strongly correlated with the relative rates of energy transfer to the rate of excited-state vibrational relaxation. A rate of energy transfer is defined as the reciprocal of the time required for the energy transfer from an excited-state donor molecule to a ground-state acceptor molecule. In the strong coupling regime, the rate of energy transfer is much larger than that of the vibrational relaxation process so that all the vibronic subtransitions associated with the energy transfer in both molecules are resonant. When the interaction is approximated by the Coulombic coupling between absorption and emission dipoles, the rate (i.e., efficiency) of energy transfer is inversely proportional to the third power of the distance between donor and acceptor (r−3). The strong coupling strength results in major alterations of the absorption spectrum and is thought to be possible to mediate excitation energy transfer up to 100 nm [91]. In the intermediate weak coupling regime, the rate of energy transfer is comparable to that of vibrational relaxation by an order of magnitude in which coherent energy transfer is thought to prevail. The coupling strength between fluorophores within this regime is expected to lead to minor alterations in the absorption spectrum, such as Davydov splitting of certain vibronic bands. In the very weak coupling regime, the coupling strength is much lower than the vibronic bandwidth so that the vibrational relaxation takes place prior to energy transfer. In this regime, fluorophores act independently so that it is expected that there is no alteration of the absorption spectrum. In addition, energy transfer is thought to be incoherent via FRET and is typically limited by a distance up to 10 nm. The interaction is inversely proportional to the six power of the distance between donor and acceptor (r−6). In 1974, Knox and Kenkre formalised the theory of slow dephasing coherent energy transfer based on the unification of the strong and weak coupling theories [92]. Figure 3 shows the rate of excitation transfer as a function of interaction energy as predicted by Förster for the strong, weak and very weak coupling regimes, as well as predicted by the Kenkre and Knox formalism. Both Förster’s theory and Kenkre–Knox’s formalism hypothesized that energy transfer associated with the intermediate weak coupling regime should be coherent, but little is known about this regime experimentally.
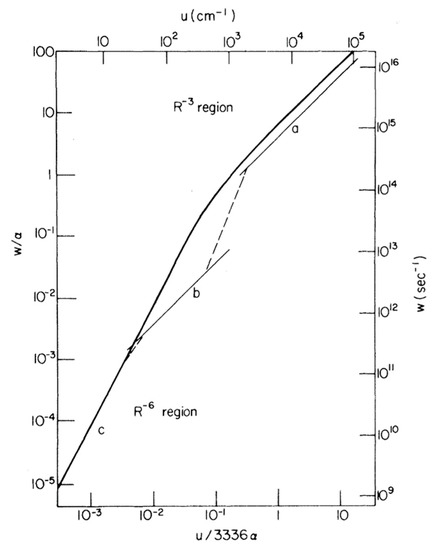
Figure 3. Comparison of transfer rates predicted by Förster for the strong, weak and very weak regimes and the formalism of Kenkre–Knox to unity the weak and strong coupling theories. Light curves (upper and right scales) correspond to Förster’s pairwise transfer rates as a function of interaction energy, u, in which curves a, b and c indicate Forster’s “strong”, intermediate “weak” and “very weak” coupling regimes, respectively. The single function predicted by Kenkre and Knox is depicted as a heavy curve (lower and left scales). The parameters α and w indicate the decay rate and the rate of energy transfer, respectively. Note that the upper and right scales are taken into account in a particular case where α = 1.8 × 1014 s−1 was chosen. Adapted from ref. [92]
3.2. Fluorescent Protein
Since the discovery of green fluorescent protein (GFP) isolated from the jellyfish Aequorea Victoria [93], FP has become an essential tool to study modern cell biology by enabling genetic protein tagging and the visualisation of cellular interactions in living cells [94]. Each FP chromophore is composed of 3 amino acids encased at the centre of a cylinder-shaped three-dimensional structure, which is the FP β-barrel. Many naturally occurring FPs tend to form dimers or tetramers [95][96][97]. Thanks to mutagenic studies, GFP can be genetically engineered to optimise its photophysical properties such as absorption/emission spectra and brightness for bioimaging applications. For example, enhanced GFP (eGFP) [98] presents a higher fluorescence than that of wild-type GFP and yellow fluorescent protein (YFP) emits light in the yellow spectrum [99]. Both eGFP and YFP are derivatives from wild-type GFP. Modification of the sequences allow further improvement of the photophysical properties of FP so that FPs are used to perform measurements of intracellular compounds and expression levels [100][101][102][103].
Nascent FPs are colourless and so must undergo maturation to become fluorescent. The maturation process involves the folding of the β-barrel, torsional rearrangements, cyclization, oxidation and dehydration of the chromophore [104]. For example, the chromophore of GFP is formed by the autocatalytical post-translational modification of 3 amino acids (Ser65-Tyr66-Gly67) [98] and is embedded in the β-barrel that has a diameter of 24 Å and a height of 42 Å [105]. The β-barrel is thought to play a role as a molecular bumper by isolating the fluorophore from molecular collisions caused by the external vibrational environment [106]. Thus, FPs are less accessible to external quenchers whilst interacting actively with their biological environment. Within the eGFP β-barrel, there is a cavity harbouring four additional water molecules [98]. This interaction with the medium is necessary for proper function in terms of FP florescence as dried films of eGFP showed a decreased fluorescence to ∼1/3 of the peak value of the hydrated protein [102]. The β-barrel is also thought to be implicated in limiting the proximity between adjacent fluorophores and to play a role to avoid self-quenching [102]. Structure-guided evolution of cyan fluorescent protein (CFP) leads to the creation of mTurquoise2, this mutagenic study in conjunction with X-ray crystallography provides evidence that modification of the β-barrel affects the brightness, maturation rate, photostability, fluorescence lifetime and even the quantum yield [107].
3.3. Förster Resonance Energy Transfer
FRET is a nonradiative energy transfer mechanism mediated by Coulombic dipole-dipole coupling, by which excitation energy is transferred from an excited-state donor molecule to a ground-state acceptor molecule. Upon excitation, FRET occurs at close proximity (typically a range of 1–10 nm) with spectral overlap and appropriate relative dipole orientation between the donor and the acceptor fluorophores [108]. When donor and acceptor fluorophores have common atomic transitions, then energy transfer proceeds discretely via the FRET mechanism.
Applications of FRET spectroscopy and microscopy in life science have rapidly increased over the past two decades because of the usefulness of FRET for proximity detection [108][109]. The extensive use of FPs for FRET measurements [109][110] as a ‘‘spectroscopic ruler’’ [111] has assumed that energy transfer between fluorophores takes place via an incoherent FRET mechanism [112][113]. This assumption is based on the understanding that coherent energy transfer between adjacent fluorophores will be prevented at the distances between donor and acceptor limited by the FP β-barrel structure. Moreover, physiological conditions are thought to promote rapid vibrational decoherence, thereby causing incoherent energy transfer [114] in which fluorophores behave independently, and excitation energy is transferred discretely from a donor to an acceptor. However, it has been observed that FPs show anomalous photophysical behaviour that cannot be explicitly explained by the theory of the very weak coupling [115][116][117][118][119][120][121][122][123][124], suggesting the possibility that excitation energy can be transferred coherently between FPs, even under physiological conditions.
3.4. Anomalous Photophysical Properties of Fluorescent Proteins
Cinelli et al. reported in 2001 that, at room temperature, the nonstationary dynamics associated with vibronic wave packets in GFP involved a dephasing time of ∼1 ps [115], which is ∼50 times slower than organic fluorophores [125]. In this study, an oscillatory modulation of the differential optical transmissivity after femtosecond laser excitation was observed and used to characterise the coherent dynamics of single-electron vibronic wave packets in GFP [115]. In 2005, Jung et al. utilized polarisation transient absorption spectroscopy to observe the rate of energy transfer among YFP dimers and reported a 2.2 ps anisotropy decay constant, which corresponds to a bidirectional energy flow with a time constant of 4.4 ps [126], which is a surprisingly fast time considering a lifetime of YFP (∼3 ns) [127]. According to the formalism of Knox and Kenkre [128], these results may be attributed to coherent energy transfer between FPs associated with the intermediate weak coupling regime.
Circular dichroism (CD) absorption spectroscopy is one of the most powerful techniques for stereochemical analysis. CD is the difference between the absorption of left and right circularly polarized light and can be used to identify the position of electronic bands and study the electronic coupling associated with the strong and intermediate coupling regimes (manifested by Davydov splitting) [129][130][131]. Visser et al. studied CD spectra from blue fluorescent protein (BFP), CFP, eGFP, and YFP, which are variants of GFP, and tetrameric Discosoma sp. red fluorescent protein (DsRed) [132]. In this study, DsRed presented a CD spectrum with an exitonic signature at the inflection point of the low-wavelength edge of the absorption band, whilst the other FPs CD spectra coincided with their absorbance spectra. These results suggest stronger than expected coupling between the chromophores in DsRed [132]. Note that DsRed oligomerisation, to form tetramers containing four chromophores, occurs even at low concentrations. Photon antibunching was detected using a scanning confocal microscope with single molecule sensitivity, indicating that, upon excitation, single chromophore emits photons one at a time, rather than, as might be expected for an entirely classical system, the four chromophores emitting photons independently of each other [133].
In 2009, Koushik et al. performed FRET measurements using multiple FRET acceptors and consecutively observed anomalous surplus energy transfer. In this study, predictions based on a FRET model underestimated the experimentally observed energy transfer efficiency. The authors concluded that either the theoretical assumptions of the FRET model are incorrect for this system, or additional energy transfer pathways were active [134].
3.5. Generation of Polarisation-Entangled Photon Pairs in an Ensemble of eGFP Molecules
3.5. Generation of Polarisation-Entangled Photon Pairs in an Ensemble of eGFP Molecules
Thanks to recent advances in techniques for optical spectroscopy, it has been become possible to precisely manipulate and monitor light for the study of light-matter interactions in biological systems. In 2016, Shi et al. reported that, unlike organic fluorophores, eGFP is less affected by background noise in response to the generation of spontaneous four wave mixing (SFWM). In this study, eGFP demonstrated a coincidence-to-accidental ratio (CAR) of ∼145, which is ~10 times larger than that of the best performing organic fluorophore, pyrromethene 556 whose CAR is ∼15 [135]. In 2017, the same group demonstrated the generation of polarisation entangled photonic states from the SFWM process in an ensemble of eGFP molecules at room temperature through two horizontally and two vertical polarized pump pulses [136]. The data were used to reconstruct the density matrix of the entangled photonic states. The result indicates that eGFP fluorophores are relatively insensitive to environment/thermal decoherence, which may be attributed to the isolation of an encapsulated fluorophore inside the FP β-barrel structure [137].
3.6. Exciton Coupling in Homodimers of Yellow Fluorescent Protein VenusA206
3.6. Exciton Coupling in Homodimers of Yellow Fluorescent Protein VenusA206
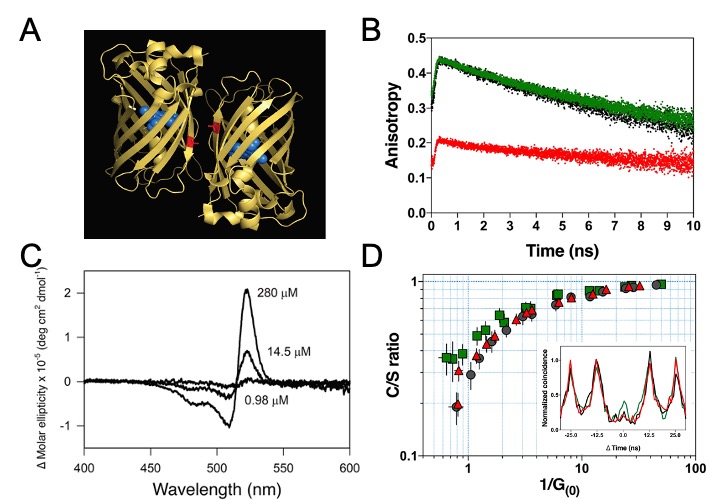
In 2019, further experimental evidence for room temperature coherent molecular in- teractions between FP fluorophores was obtained by Kim et al. The study reported unexpected FP quantum behaviour resulting from excitonic coupling in homodimers of dimeric yellow fluorescent protein VenusA206 under physiological conditions (Figure 4A) [138]. Time-resolved fluorescence anisotropy measurements were used to reveal ultrafast energy transfer (defined as faster than the instrument response function of the anisotropy system, ~146 ps) between FP fluorophores when VenusA206 FPs dimerise (Figure 4B). CD absorption spectroscopy revealed Davydov-splitting (Figure 4C) in VenusA206 dimers, which is a quantum mechanical manifestation of fluorophore excitonic coupling. Moreover, a novel approach combining photon antibunching (AB) with fluorescence correlation spectroscopy (FCS), AB/FCS fingerprinting, was used to compare the number of independent emitters and fluorescent fluctuating molecules in the same sample. Figure 4D shows the results of the AB/FCS fingerprints for monomeric VenusA206K (Black), monomeric VenusA206K tandem dimer with the Venus fluorophores separated by a 20 nm linker (VenusA206K-20nm-TD, Green) and dimeric VenusA206 tandem dimer (VenusA206-TD, Red), which indicate that the VenusA206-TD behaves as a single quantum entity. Alteration of VenusA206-TD emission behaviour as a result of exciton coupling between FP fluorophores again provides strong evidence for quantum coherent molecular interactions. Note that singlet-singlet annihilation, which is an alternative classical description for reducing two excitation events to one emission event and is supposed to be dependent on excitation power, cannot be employed to explain strong AB in VenusA206-TD since a dependence on excitation power was not observed. It is also noteworthy that FPs encase a single fluorophore within β-barrel structure that are easily modified by genetic engineering techniques, making them ideal tools as well as novel model systems for studies of quantum effects in a biological system.
Figure 4. Quantum signatures observed in homodimers of yellow fluorescent protein, VenusA206, when they dimerise. (A). An illustration of a pair of dimeric VenusA206 molecules based on the crystal structure. Venus chromophore and its β- barrel are depicted as blue spheres and yellow ribbon structures, respectively. A residual, alanine-206, that involves in dimerization is depicted as red. The separation proximity between centre-to-centre FP fluorophores in crystals is 2.5 nm, and the closest distance between its fluorophores is 1.5 nm. (B). Time-resolved fluorescence anisotropy of VenusA206K (Black), monomeric VenusA206K-20nm-TD (Green), and VenusA206-TD (Red). (C). Dimerization alters its circular dichroism spectrum that results in Davydov splitting. For each fluorophore concentration, the VenusA206 CD absorption spectrum was subtracted from its matching CD spectrum of VenusA206K. (D). AB/FCS fingerprints for the three samples. The inset shows the antibunching measurements of VenusA206K (black), VenusA206-TD (red) and VenusA206K-20 nm-TD (green). Adapted from ref. [138].
3.7. Conclusions and Outlook
It is apparent that the results of the generation of photonic entanglement in eGFP [136] and excitonic coupling between dimeric VenusA206 FPs [138] at room temperature support the hypothesis that FPs have evolved a mechanism to prolong quantum coherence under physiological conditions and might therefore have unique photophysical properties. FP is a simple, accessible and amenable system that can be genetically manipulated. Moreover, a unique advantage of FPs over other probes, such as organic dyes, is that they are resistant to the presence of external quenchers [137] as well as presenting a high quantum efficacy [139]. Application of these approaches will provide an insight into understanding how biological systems maintain quantum effects in a warm, wet and complex biological environment as well as how such quantum effects influence biological processes and behaviours. Furthermore, knowledge learned from these approaches may open a new avenue towards quantum-bio-inspired technologies, such as the development of efficient quantum light sources and next-generation biosensors that exploit quantum behaviour.
4. Conclusions
4. Conclusions
It is clear that quantum biology is a growing area of interdisciplinary research with contributions from quantum physicists, molecular biologists, biochemists, mathematicians, engineers, chemists and spectroscopists. As described here, important advances have been made in the well-established fields, such as photosynthesis, enzyme catalysis and avian navigation, as well as in less established areas, such as fluorescent proteins, ion channels and proton tunnelling in DNA. Yet questions and challenges remain. Although there is no doubt that the molecular machinery of life involves the motion of individual electrons or protons that necessarily involves quantum phenomena such as coherence, tunnelling or entanglement, establishing a biological function for these quantum features remains a challenge. For obvious reasons, most experimental data have been obtained from in vitro systems capable of generating measurable signals. However, even the best available in vitro systems, such as photosynthetic complexes and whole enzymes, consist of thousands or millions of atoms that are already too complex to realistically model at the quantum level. One approach to address this problem, as outlined in this review, is to utilise nanotechnology approaches to build biomimetic systems that are simpler than their biological counterparts and thereby more amenable to mathematical modelling and computation. This is clearly a fruitful area for further development and even technological applications.
Nevertheless, in vitro systems, even biomimetic ones, are unlikely to convince the sceptics that quantum biology is relevant to life. Proof requires demonstration that quantum phenomena play a role in biological function in living cells and thereby contribute to fitness. Yet quantum biological phenomena have only so far been investigated in a limited range of organisms, most of which, such as birds or photosynthetic bacteria, are relatively intractable to the powerful tools of molecular biology and synthetic biology. The challenge of the future will be to transfer measurable quantum biological systems into the more tractable workhorses of molecular biology and synthetic biology, such as E. coli or yeast, to engineer system that allow simultaneous detection of quantum level events and their macroscopic outcomes. This challenge will require a new generation of scientists who can work across the disciplines of physics, chemistry and biology. This is not a new challenge. The discipline of biochemistry necessitated a similar merging of chemistry with biology about a hundred years ago. It required the training of a new generation of students and researchers able to take on the challenge of working at an interdisciplinary frontier.
References
- McFadden, J.; Al-Khalili, J. The origins of quantum biology. Proc. R. Soc. A 2018, 474, 20180674.
- Schrodinger, E. What Is Life; Cambridge University Press: Cambridge, UK, 1944.
- Melkikh, A.V.; Khrennikov, A. Nontrivial quantum and quantum-like effects in biosystems: Unsolved questions and paradoxes. Prog. Biophys. Mol. Biol. 2015, 119, 137–161.
- Bassham, J.A.; Calvin, M. The path of carbon in photosynthesis. In Die CO2-Assimilation/The Assimilation of Carbon Dioxide; Springer: Berlin/Heidelberg, Germany, 1960; pp. 884–922.
- Bolton, J.R.; Hall, D.O. The maximum efficiency of photosynthesis. Photochem. Photobiol. 1991, 53, 545–548.
- Zhu, X.-G.; Long, S.P.; Ort, D.R. What is the maximum efficiency with which photosynthesis can convert solar energy into biomass? Curr. Opin. Biotechnol. 2008, 19, 153–159.
- Chen, G.-Y.; Lambert, N.; Li, C.-M.; Chen, Y.-N.; Nori, F. Rerouting excitation transfers in the Fenna-Matthews-Olson complex. Phys. Rev. E 2013, 88, 032120.
- Panitchayangkoon, G.; Voronine, D.V.; Abramavicius, D.; Caram, J.R.; Lewis, N.H.; Mukamel, S.; Engel, G.S. Direct evidence of quantum transport in photosynthetic light-harvesting complexes. Proc. Natl. Acad. Sci. USA 2011, 108, 20908–20912.
- Förster, T. Transfer mechanisms of electronic excitation energy. Radiat. Res. Suppl. 1960, 2, 326–339.
- Perrin, F. Théorie quantique des transferts d’activation entre molécules de même espèce. Cas des solutions fluorescentes. Ann. Phys. 1932, 10, 283–314.
- Forster, T. Energiewanderung und fluoreszenz. Naturwissenschaften 1946, 33, 166–175.
- Alden, R.; Johnson, E.; Nagarajan, V.; Parson, W.; Law, C.; Cogdell, R. Calculations of Spectroscopic Properties of the LH2 Bacteriochlorophyll− Protein Antenna Complex from Rhodopseudomonas Acidophila. J. Phys. Chem. B 1997, 101, 4667–4680.
- Chachisvilis, M.; Kühn, O.; Pullerits, T.; Sundström, V. Excitons in photosynthetic purple bacteria: Wavelike motion or incoherent hopping? J. Phys. Chem. B 1997, 101, 7275–7283.
- Jang, S.; Newton, M.D.; Silbey, R.J. Multichromophoric Förster resonance energy transfer from B800 to B850 in the light harvesting complex 2: Evidence for subtle energetic optimization by purple bacteria. J. Phys. Chem. B 2007, 111, 6807–6814.
- Olbrich, C.; Jansen, T.L.; Liebers, J.; Aghtar, M.; Strümpfer, J.; Schulten, K.; Knoester, J.; Kleinekathöfer, U. From atomistic modeling to excitation transfer and two-dimensional spectra of the FMO light-harvesting complex. J. Phys. Chem. B 2011, 115, 8609–8621.
- Sauer, K.; Cogdell, R.J.; Prince, S.M.; Freer, A.; Isaacs, N.W.; Scheer, H. Structure-based calculations of the optical spectra of the LH2 bacteriochlorophyll-protein complex from Rhodopseudomonas acidophila. Photochem. Photobiol. 1996, 64, 564–576.
- Scholes, G.D.; Gould, I.R.; Cogdell, R.J.; Fleming, G.R. Ab initio molecular orbital calculations of electronic couplings in the LH2 bacterial light-harvesting complex of Rps. acidophila. J. Phys. Chem. B 1999, 103, 2543–2553.
- Blankenship, R.E. Molecular Mechanisms of Photosynthesis; John Wiley & Sons: Hoboken, NJ, USA, 2014.
- Fleming, G.R.; van Grondelle, R. Femtosecond spectroscopy of photosynthetic light-harvesting systems. Curr. Opin. Struct. Biol. 1997, 7, 738–748.
- Van Amerongen, H.; Van Grondelle, R. Photosynthetic Excitons; World Scientific: Singapore, 2000.
- Nakamura, Y.; Aratani, N.; Osuka, A. Cyclic porphyrin arrays as artificial photosynthetic antenna: Synthesis and excitation energy transfer. Chem. Soc. Rev. 2007, 36, 831–845.
- Fassioli, F.; Dinshaw, R.; Arpin, P.C.; Scholes, G.D. Photosynthetic light harvesting: Excitons and coherence. J. R. Soc. Interface 2014, 11, 20130901.
- Jumper, C.C.; Rafiq, S.; Wang, S.; Scholes, G.D. From coherent to vibronic light harvesting in photosynthesis. Curr. Opin. Chem. Biol. 2018, 47, 39–46.
- Hsu, C.-P. The electronic couplings in electron transfer and excitation energy transfer. Acc. Chem. Res. 2009, 42, 509–518.
- Seibt, J.; Mančal, T. Ultrafast energy transfer with competing channels: Non-equilibrium Förster and Modified Redfield theories. J. Chem. Phys. 2017, 146, 174109.
- Tao, M.-J.; Zhang, N.-N.; Wen, P.-Y.; Deng, F.-G.; Ai, Q.; Long, G.-L. Coherent and incoherent theories for photosynthetic energy transfer. Sci. Bull. 2020, 65, 318–328.
- Ishizaki, A.; Tanimura, Y. Quantum dynamics of system strongly coupled to low-temperature colored noise bath: Reduced hierarchy equations approach. J. Phys. Soc. Jpn. 2005, 74, 3131–3134.
- Ishizaki, A.; Fleming, G.R. Theoretical examination of quantum coherence in a photosynthetic system at physiological temperature. Proc. Natl. Acad. Sci. USA 2009, 106, 17255–17260.
- Lambert, N.; Ahmed, S.; Cirio, M.; Nori, F. Modelling the ultra-strongly coupled spin-boson model with unphysical modes. Nat. Commun. 2019, 10, 1–9.
- Prior, J.; Chin, A.W.; Huelga, S.F.; Plenio, M.B. Efficient simulation of strong system-environment interactions. Phys. Rev. Lett. 2010, 105, 050404.
- Chin, A.W.; Rivas, Á.; Huelga, S.F.; Plenio, M.B. Exact mapping between system-reservoir quantum models and semi-infinite discrete chains using orthogonal polynomials. J. Math. Phys. 2010, 51, 092109.
- Chin, A.W.; Huelga, S.F.; Plenio, M.B. Chain representations of open quantum systems and their numerical simulation with time-adaptive density matrix renormalisation group methods. In Semiconductors and Semimetals; Elsevier: Amsterdam, The Netherlands, 2011; Volume 85, pp. 115–143.
- Chin, A.; Prior, J.; Rosenbach, R.; Caycedo-Soler, F.; Huelga, S.F.; Plenio, M.B. The role of non-equilibrium vibrational structures in electronic coherence and recoherence in pigment–protein complexes. Nat. Phys. 2013, 9, 113–118.
- Gelzinis, A.; Augulis, R.; Butkus, V.; Robert, B.; Valkunas, L. Two-dimensional spectroscopy for non-specialists. Biochim. Biophys. Acta Bioenerg. 2019, 1860, 271–285.
- Wang, L.; Allodi, M.A.; Engel, G.S. Quantum coherences reveal excited-state dynamics in biophysical systems. Nat. Rev. Chem. 2019, 3, 477–490.
- Lewis, K.L.; Ogilvie, J.P. Probing photosynthetic energy and charge transfer with two-dimensional electronic spectroscopy. J. Phys. Chem. Lett. 2012, 3, 503–510.
- Ostroumov, E.E.; Mulvaney, R.M.; Cogdell, R.J.; Scholes, G.D. Broadband 2D electronic spectroscopy reveals a carotenoid dark state in purple bacteria. Science 2013, 340, 52–56.
- Panitchayangkoon, G.; Hayes, D.; Fransted, K.A.; Caram, J.R.; Harel, E.; Wen, J.; Blankenship, R.E.; Engel, G.S. Long-lived quantum coherence in photosynthetic complexes at physiological temperature. Proc. Natl. Acad. Sci. USA 2010, 107, 12766–12770.
- Chin, A.W.; Huelga, S.F.; Plenio, M.B. Quantum metrology in non-Markovian environments. Phys. Rev. Lett. 2012, 109, 233601.
- Baghbanzadeh, S.; Kassal, I. Distinguishing the roles of energy funnelling and delocalization in photosynthetic light harvesting. Phys. Chem. Chem. Phys. 2016, 18, 7459–7467.
- Engel, G.S.; Calhoun, T.R.; Read, E.L.; Ahn, T.-K.; Mančal, T.; Cheng, Y.-C.; Blankenship, R.E.; Fleming, G.R. Evidence for wavelike energy transfer through quantum coherence in photosynthetic systems. Nature 2007, 446, 782–786.
- Sarovar, M.; Ishizaki, A.; Fleming, G.R.; Whaley, K.B. Quantum entanglement in photosynthetic light-harvesting complexes. Nat. Phys. 2010, 6, 462–467.
- Cao, J.; Cogdell, R.J.; Coker, D.F.; Duan, H.-G.; Hauer, J.; Kleinekathöfer, U.; Jansen, T.L.; Mančal, T.; Miller, R.D.; Ogilvie, J.P. Quantum biology revisited. Sci. Adv. 2020, 6, eaaz4888.
- Lee, H.; Cheng, Y.-C.; Fleming, G.R. Coherence dynamics in photosynthesis: Protein protection of excitonic coherence. Science 2007, 316, 1462–1465.
- Ryu, I.S.; Dong, H.; Fleming, G.R. Role of electronic-vibrational mixing in enhancing vibrational coherences in the ground electronic states of photosynthetic bacterial reaction center. J. Phys. Chem. B 2014, 118, 1381–1388.
- Ma, F.; Romero, E.; Jones, M.R.; Novoderezhkin, V.I.; van Grondelle, R. Both electronic and vibrational coherences are involved in primary electron transfer in bacterial reaction center. Nat. Commun. 2019, 10, 1–9.
- Christensson, N.; Kauffmann, H.F.; Pullerits, T.; Mancal, T. Origin of long-lived coherences in light-harvesting complexes. J. Phys. Chem. B 2012, 116, 7449–7454.
- Thyrhaug, E.; Tempelaar, R.; Alcocer, M.J.; Žídek, K.; Bína, D.; Knoester, J.; Jansen, T.L.; Zigmantas, D. Identification and characterization of diverse coherences in the Fenna–Matthews–Olson complex. Nat. Chem. 2018, 10, 780–786.
- Dean, J.C.; Mirkovic, T.; Toa, Z.S.; Oblinsky, D.G.; Scholes, G.D. Vibronic enhancement of algae light harvesting. Chem 2016, 1, 858–872.
- Tiwari, V.; Peters, W.K.; Jonas, D.M. Electronic resonance with anticorrelated pigment vibrations drives photosynthetic energy transfer outside the adiabatic framework. Proc. Natl. Acad. Sci. USA 2013, 110, 1203–1208.
- Paleček, D.; Edlund, P.; Westenhoff, S.; Zigmantas, D. Quantum coherence as a witness of vibronically hot energy transfer in bacterial reaction center. Sci. Adv. 2017, 3, e1603141.
- Calhoun, T.R.; Ginsberg, N.S.; Schlau-Cohen, G.S.; Cheng, Y.-C.; Ballottari, M.; Bassi, R.; Fleming, G.R. Quantum coherence enabled determination of the energy landscape in light-harvesting complex II. J. Phys. Chem. B 2009, 113, 16291–16295.
- Collini, E.; Wong, C.Y.; Wilk, K.E.; Curmi, P.M.; Brumer, P.; Scholes, G.D. Coherently wired light-harvesting in photosynthetic marine algae at ambient temperature. Nature 2010, 463, 644–647.
- Romero, E.; Augulis, R.; Novoderezhkin, V.I.; Ferretti, M.; Thieme, J.; Zigmantas, D.; Van Grondelle, R. Quantum coherence in photosynthesis for efficient solar-energy conversion. Nat. Phys. 2014, 10, 676–682.
- Karki, K.J.; Chen, J.; Sakurai, A.; Shi, Q.; Gardiner, A.T.; Kühn, O.; Cogdell, R.J.; Pullerits, T. Before Förster. Initial excitation in photosynthetic light harvesting. Chem. Sci. 2019, 10, 7923–7928.
- Irgen-Gioro, S.; Gururangan, K.; Saer, R.G.; Blankenship, R.E.; Harel, E. Electronic coherence lifetimes of the Fenna–Matthews–Olson complex and light harvesting complex II. Chem. Sci. 2019, 10, 10503–10509.
- Hildner, R.; Brinks, D.; Nieder, J.B.; Cogdell, R.J.; van Hulst, N.F. Quantum coherent energy transfer over varying pathways in single light-harvesting complexes. Science 2013, 340, 1448–1451.
- Chin, A.; Huelga, S.F.; Plenio, M.B. Coherence and decoherence in biological systems: Principles of noise-assisted transport and the origin of long-lived coherences. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2012, 370, 3638–3657.
- Harel, E.; Engel, G.S. Quantum coherence spectroscopy reveals complex dynamics in bacterial light-harvesting complex 2 (LH2). Proc. Natl. Acad. Sci. USA 2012, 109, 706–711.
- Fischer, M.; Gutiérrez-Medina, B.; Raizen, M. Observation of the quantum Zeno and anti-Zeno effects in an unstable system. Phys. Rev. Lett. 2001, 87, 040402.
- Rebentrost, P.; Mohseni, M.; Kassal, I.; Lloyd, S.; Aspuru-Guzik, A. Environment-assisted quantum transport. New J. Phys. 2009, 11, 033003.
- Mohseni, M.; Shabani, A.; Lloyd, S.; Rabitz, H. Energy-scales convergence for optimal and robust quantum transport in photosynthetic complexes. J. Chem. Phys. 2014, 140, 01B609_601.
- Jang, S.J. Robust and Fragile Quantum Effects in the Transfer Kinetics of Delocalized Excitons between B850 Units of LH2 Complexes. J. Phys. Chem. Lett. 2018, 9, 6576–6583.
- Prokhorenko, V.I.; Nagy, A.M.; Waschuk, S.A.; Brown, L.S.; Birge, R.R.; Miller, R.D. Coherent control of retinal isomerization in bacteriorhodopsin. Science 2006, 313, 1257–1261.
- Bickel-Sandkötter, S.; Gärtner, W.; Dane, M. Conversion of energy in halobacteria: ATP synthesis and phototaxis. Arch. Microbiol. 1996, 166, 1–11.
- Oren, A. The order halobacteriales. Prokaryotes 2006, 3, 113–164.
- Frydrych, M.; Silfsten, P.; Parkkinen, S.; Parkkinen, J.; Jaaskelainen, T. Color sensitive retina based on bacteriorhodopsin. Biosystems 2000, 54, 131–140.
- Hampp, N. Bacteriorhodopsin as a photochromic retinal protein for optical memories. Chem. Rev. 2000, 100, 1755–1776.
- Margesin, R.; Schinner, F. Potential of halotolerant and halophilic microorganisms for biotechnology. Extremophiles 2001, 5, 73–83.
- Rakovich, A.; Sukhanova, A.; Bouchonville, N.; Lukashev, E.; Oleinikov, V.; Artemyev, M.; Lesnyak, V.; Gaponik, N.; Molinari, M.; Troyon, M. Resonance energy transfer improves the biological function of bacteriorhodopsin within a hybrid material built from purple membranes and semiconductor quantum dots. Nano Lett. 2010, 10, 2640–2648.
- Ghosh, P.K.; Smirnov, A.Y.; Nori, F. Modeling light-driven proton pumps in artificial photosynthetic reaction centers. J. Chem. Phys. 2009, 131, 07B610.
- Proppe, A.H.; Li, Y.C.; Aspuru-Guzik, A.; Berlinguette, C.P.; Chang, C.J.; Cogdell, R.; Doyle, A.G.; Flick, J.; Gabor, N.M.; van Grondelle, R. Bioinspiration in light harvesting and catalysis. Nat. Rev. Mater. 2020, 5, 828–846.
- Lee, S.H.; Matula, A.J.; Hu, G.; Troiano, J.L.; Karpovich, C.J.; Crabtree, R.H.; Batista, V.S.; Brudvig, G.W. Strongly coupled phenazine–porphyrin dyads: Light-harvesting molecular assemblies with broad absorption coverage. ACS Appl. Mater. Interfaces 2019, 11, 8000–8008.
- Prinz, J.-H.; Wu, H.; Sarich, M.; Keller, B.; Senne, M.; Held, M.; Chodera, J.D.; Schütte, C.; Noé, F. Markov models of molecular kinetics: Generation and validation. J. Chem. Phys. 2011, 134, 174105.
- Ghosh, P.K.; Smirnov, A.Y.; Nori, F. Quantum effects in energy and charge transfer in an artificial photosynthetic complex. J. Chem. Phys. 2011, 134, 06B611.
- Roscioli, J.D.; Ghosh, S.; LaFountain, A.M.; Frank, H.A.; Beck, W.F. Structural Tuning of Quantum Decoherence and Coherent Energy Transfer in Photosynthetic Light Harvesting. J. Phys. Chem. Lett. 2018, 9, 5071–5077.
- Delor, M.; Dai, J.; Roberts, T.D.; Rogers, J.R.; Hamed, S.M.; Neaton, J.B.; Geissler, P.L.; Francis, M.B.; Ginsberg, N.S. Exploiting chromophore–protein interactions through linker engineering to tune photoinduced dynamics in a biomimetic light-harvesting platform. J. Am. Chem. Soc. 2018, 140, 6278–6287.
- Wang, L.; Griffin, G.B.; Zhang, A.; Zhai, F.; Williams, N.E.; Jordan, R.F.; Engel, G.S. Controlling quantum-beating signals in 2D electronic spectra by packing synthetic heterodimers on single-walled carbon nanotubes. Nat. Chem. 2017, 9, 219.
- Freixas, V.; Tretiak, S.; Makhov, D.V.; Shalashilin, D.V.; Fernandez-Alberti, S. Vibronic Quantum Beating between Electronic Excited States in a Heterodimer. J. Phys. Chem. B 2020, 124, 3992–4001.
- McCleese, C.; Yu, Z.; Esemoto, N.N.; Kolodziej, C.; Maiti, B.; Bhandari, S.; Dunietz, B.D.; Burda, C.; Ptaszek, M. Excitonic interactions in bacteriochlorin homo-dyads enable charge transfer: A new approach to the artificial photosynthetic special pair. J. Phys. Chem. B 2018, 122, 4131–4140.
- Tiwari, V.; Matutes, Y.A.; Konar, A.; Yu, Z.; Ptaszek, M.; Bocian, D.F.; Holten, D.; Kirmaier, C.; Ogilvie, J.P. Strongly coupled bacteriochlorin dyad studied using phase-modulated fluorescence-detected two-dimensional electronic spectroscopy. Opt. Express 2018, 26, 22327–22341.
- Shoji, S.; Tamiaki, H. Supramolecular light-harvesting antenna system by co-aggregates of zinc (bacterio) chlorophyll-a derivatives with biomimetic chlorosomal self-assemblies. Dye. Pigment. 2019, 160, 514–518.
- Shoji, S.; Nomura, Y.; Tamiaki, H. Heterodimers of zinc and free-base chlorophyll derivatives co-assembled in biomimetic chlorosomal J-aggregates. Photochem. Photobiol. Sci. 2019, 18, 555–562.
- Pandya, R.; Chen, R.Y.; Cheminal, A.; Thomas, T.; Thampi, A.; Tanoh, A.; Richter, J.; Shivanna, R.; Deschler, F.; Schnedermann, C. Observation of Vibronic-Coupling-Mediated Energy Transfer in Light-Harvesting Nanotubes Stabilized in a Solid-State Matrix. J. Phys. Chem. Lett. 2018, 9, 5604–5611.
- Kim, T.; Ham, S.; Lee, S.H.; Hong, Y.; Kim, D. Enhancement of exciton transport in porphyrin aggregate nanostructures by controlling the hierarchical self-assembly. Nanoscale 2018, 10, 16438–16446.
- Lloyd, S.; Mohseni, M. Symmetry-enhanced supertransfer of delocalized quantum states. New J. Phys. 2010, 12, 075020.
- Chuang, C.; Lee, C.K.; Moix, J.M.; Knoester, J.; Cao, J. Quantum diffusion on molecular tubes: Universal scaling of the 1D to 2D transition. Phys. Rev. Lett. 2016, 116, 196803.
- Lim, J.; Paleček, D.; Caycedo-Soler, F.; Lincoln, C.N.; Prior, J.; Von Berlepsch, H.; Huelga, S.F.; Plenio, M.B.; Zigmantas, D.; Hauer, J. Vibronic origin of long-lived coherence in an artificial molecular light harvester. Nat. Commun. 2015, 6, 1–7.
- Butkus, V.; Alster, J.; Bašinskaitė, E.; Augulis, R.N.; Neuhaus, P.; Valkunas, L.; Anderson, H.L.; Abramavicius, D.; Zigmantas, D. Discrimination of diverse coherences allows identification of electronic transitions of a molecular nanoring. J. Phys. Chem. Lett. 2017, 8, 2344–2349.
- Förster, T. Delocalized Excitation and Excitation Transfer; Sinanoglu, O., Ed.; Modern Quantum Chemistry. Istanbul Lectures 3; Academic Press: New York, NY, USA; London, UK, 1965.
- Clegg, R.M. The history of FRET. In Reviews in Fluorescence 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1–45.
- Kenkre, V.; Knox, R. Theory of fast and slow excitation transfer rates. Phys. Rev. Lett. 1974, 33, 803.
- Tsien, R.Y. The green fluorescent protein. Annu. Rev. Biochem. 1998, 67, 509–544.
- Rodriguez, E.A.; Campbell, R.E.; Lin, J.Y.; Lin, M.Z.; Miyawaki, A.; Palmer, A.E.; Shu, X.; Zhang, J.; Tsien, R.Y. The growing and glowing toolbox of fluorescent and photoactive proteins. Trends Biochem. Sci. 2017, 42, 111–129.
- Gross, L.A.; Baird, G.S.; Hoffman, R.C.; Baldridge, K.K.; Tsien, R.Y. The structure of the chromophore within DsRed, a red fluorescent protein from coral. Proc. Natl. Acad. Sci. USA 2000, 97, 11990–11995.
- Shaner, N.C.; Lambert, G.G.; Chammas, A.; Ni, Y.; Cranfill, P.J.; Baird, M.A.; Sell, B.R.; Allen, J.R.; Day, R.N.; Israelsson, M. A bright monomeric green fluorescent protein derived from Branchiostoma lanceolatum. Nat. Methods 2013, 10, 407–409.
- Ward, W.; Cormier, M. Energy transfer protein in coelenterate bioluminescence. J. Biol. Chem. 1979, 254, 781–788.
- Arpino, J.A.; Rizkallah, P.J.; Jones, D.D. Crystal structure of enhanced green fluorescent protein to 1.35 Å resolution reveals alternative conformations for Glu222. PLoS ONE 2012, 7, e47132.
- Taghizadeh, R.R.; Sherley, J.L. CFP and YFP, but not GFP, provide stable fluorescent marking of rat hepatic adult stem cells. J. Biomed. Biotechnol. 2008, 2008, 453590.
- Chudakov, D.M.; Lukyanov, S.; Lukyanov, K.A. Fluorescent proteins as a toolkit for in vivo imaging. Trends Biotechnol. 2005, 23, 605–613.
- Hebisch, E.; Knebel, J.; Landsberg, J.; Frey, E.; Leisner, M. High variation of fluorescence protein maturation times in closely related Escherichia coli strains. PLoS ONE 2013, 8, e75991.
- Gather, M.C.; Yun, S.H. Bio-optimized energy transfer in densely packed fluorescent protein enables near-maximal luminescence and solid-state lasers. Nat. Commun. 2014, 5, 1–8.
- Specht, E.A.; Braselmann, E.; Palmer, A.E. A critical and comparative review of fluorescent tools for live-cell imaging. Annu. Rev. Physiol. 2017, 79, 93–117.
- Balleza, E.; Kim, J.M.; Cluzel, P. Systematic characterization of maturation time of fluorescent proteins in living cells. Nat. Methods 2018, 15, 47–51.
- Sarkar, P.; Koushik, S.V.; Vogel, S.S.; Gryczynski, I.; Gryczynski, Z.K. Photophysical properties of Cerulean and Venus fluorescent proteins. J. Biomed. Opt. 2009, 14, 034047.
- Gilmore, J.; McKenzie, R.H. Spin boson models for quantum decoherence of electronic excitations of biomolecules and quantum dots in a solvent. J. Phys. Condens. Matter 2005, 17, 1735.
- Goedhart, J.; Von Stetten, D.; Noirclerc-Savoye, M.; Lelimousin, M.; Joosen, L.; Hink, M.A.; Van Weeren, L.; Gadella, T.W.; Royant, A. Structure-guided evolution of cyan fluorescent proteins towards a quantum yield of 93%. Nat. Commun. 2012, 3, 1–9.
- Clegg, R.M. The history of FRET. In Reviews in Fluorescence 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1–45.
- Algar, W.R.; Hildebrandt, N.; Vogel, S.S.; Medintz, I.L. FRET as a biomolecular research tool—understanding its potential while avoiding pitfalls. Nat. Methods 2019, 16, 815–829.
- Siegel, R.M.; Chan, F.K.-M.; Zacharias, D.A.; Swofford, R.; Holmes, K.L.; Tsien, R.Y.; Lenardo, M.J. Measurement of molecular interactions in living cells by fluorescence resonance energy transfer between variants of the green fluorescent protein. Sci. Signal. 2000, 2000, pl1.
- Stryer, L.; Haugland, R.P. Energy transfer: A spectroscopic ruler. Proc. Natl. Acad. Sci. USA 1967, 58, 719.
- Nelson, P.C. The role of quantum decoherence in FRET. Biophys. J. 2018, 115, 167–172.
- Gilmore, J.; McKenzie, R.H. Quantum dynamics of electronic excitations in biomolecular chromophores: Role of the protein environment and solvent. J. Phys. Chem. A 2008, 112, 2162–2176.
- Clegg, R.M. The history of FRET. In Reviews in Fluorescence 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1–45.
- Cinelli, R.A.; Tozzini, V.; Pellegrini, V.; Beltram, F.; Cerullo, G.; Zavelani-Rossi, M.; De Silvestri, S.; Tyagi, M.; Giacca, M. Coherent dynamics of photoexcited green fluorescent proteins. Phys. Rev. Lett. 2001, 86, 3439.
- Jung, G.; Ma, Y.; Prall, B.S.; Fleming, G.R. Ultrafast fluorescence depolarisation in the yellow fluorescent protein due to its dimerisation. ChemPhysChem 2005, 6, 1628–1632.
- Shi, S.; Kumar, P.; Lee, K.F. Generation of photonic entanglement in green fluorescent proteins. Nat. Commun. 2017, 8, 1–7.
- Kim, Y.; Puhl III, H.L.; Chen, E.; Taumoefolau, G.H.; Nguyen, T.A.; Kliger, D.S.; Blank, P.S.; Vogel, S.S. VenusA206 Dimers Behave Coherently at Room Temperature. Biophys. J. 2019, 116, 1918–1930.
- Dietrich, C.P.; Steude, A.; Tropf, L.; Schubert, M.; Kronenberg, N.M.; Ostermann, K.; Höfling, S.; Gather, M.C. An exciton-polariton laser based on biologically produced fluorescent protein. Sci. Adv. 2016, 2, e1600666.
- Sánchez-Mosteiro, G.; Koopman, M.; van Dijk, E.M.; Hernando, J.; van Hulst, N.F.; García-Parajó, M.F. Photon antibunching proves emission from a single subunit in the autofluorescent protein DsRed. ChemPhysChem 2004, 5, 1782–1785.
- Visser, N.V.; Hink, M.A.; Borst, J.W.; van der Krogt, G.N.; Visser, A.J. Circular dichroism spectroscopy of fluorescent proteins. FEBS Lett. 2002, 521, 31–35.
- Koushik, S.V.; Blank, P.S.; Vogel, S.S. Anomalous surplus energy transfer observed with multiple FRET acceptors. PLoS ONE 2009, 4, e8031.
- Lounis, B.; Deich, J.; Rosell, F.; Boxer, S.G.; Moerner, W. Photophysics of Ds Red, a red fluorescent protein, from the ensemble to the single-molecule level. J. Phys. Chem. B 2001, 105, 5048–5054.
- Shi, S.; Thomas, A.; Corzo, N.V.; Kumar, P.; Huang, Y.; Lee, K.F. Broadband photon pair generation in green fluorescent proteins through spontaneous four-wave mixing. Sci. Rep. 2016, 6, 24344.
- Förster, T. Delocalized Excitation and Excitation Transfer; Sinanoglu, O., Ed.; Modern Quantum Chemistry. Istanbul Lectures 3; Academic Press: New York, NY, USA; London, UK, 1965.
- Jung, G.; Ma, Y.; Prall, B.S.; Fleming, G.R. Ultrafast fluorescence depolarisation in the yellow fluorescent protein due to its dimerisation. ChemPhysChem 2005, 6, 1628–1632.
- Borst, J.W.; Hink, M.A.; van Hoek, A.; Visser, A.J. Effects of refractive index and viscosity on fluorescence and anisotropy decays of enhanced cyan and yellow fluorescent proteins. J. Fluoresc. 2005, 15, 153–160.
- Kenkre, V.; Knox, R. Theory of fast and slow excitation transfer rates. Phys. Rev. Lett. 1974, 33, 803.
- Geddes, C.D.; Lakowicz, J.R. Reviews in Fluorescence 2006; Springer: Berlin/Heidelberg, Germany, 2005.
- Berova, N.; Di Bari, L.; Pescitelli, G. Application of electronic circular dichroism in configurational and conformational analysis of organic compounds. Chem. Soc. Rev. 2007, 36, 914–931.
- Grishina, I.B.; Woody, R.W. Contributions of tryptophan side chains to the circular dichroism of globular proteins: Exciton couplets and coupled oscillators. Faraday Discuss. 1994, 99, 245–262.
- Visser, N.V.; Hink, M.A.; Borst, J.W.; van der Krogt, G.N.; Visser, A.J. Circular dichroism spectroscopy of fluorescent proteins. FEBS Lett. 2002, 521, 31–35.
- Sánchez-Mosteiro, G.; Koopman, M.; van Dijk, E.M.; Hernando, J.; van Hulst, N.F.; García-Parajó, M.F. Photon antibunching proves emission from a single subunit in the autofluorescent protein DsRed. ChemPhysChem 2004, 5, 1782–1785.
- Koushik, S.V.; Blank, P.S.; Vogel, S.S. Anomalous surplus energy transfer observed with multiple FRET acceptors. PLoS ONE 2009, 4, e8031.
- Shi, S.; Thomas, A.; Corzo, N.V.; Kumar, P.; Huang, Y.; Lee, K.F. Broadband photon pair generation in green fluorescent proteins through spontaneous four-wave mixing. Sci. Rep. 2016, 6, 24344.
- Shi, S.; Kumar, P.; Lee, K.F. Generation of photonic entanglement in green fluorescent proteins. Nat. Commun. 2017, 8, 1–7.
- Gilmore, J.; McKenzie, R.H. Spin boson models for quantum decoherence of electronic excitations of biomolecules and quantum dots in a solvent. J. Phys. Condens. Matter 2005, 17, 1735.
- Kim, Y.; Puhl III, H.L.; Chen, E.; Taumoefolau, G.H.; Nguyen, T.A.; Kliger, D.S.; Blank, P.S.; Vogel, S.S. VenusA206 Dimers Behave Coherently at Room Temperature. Biophys. J. 2019, 116, 1918–1930.
- Ilagan, R.P.; Rhoades, E.; Gruber, D.F.; Kao, H.T.; Pieribone, V.A.; Regan, L. A new bright green-emitting fluorescent protein–engineered monomeric and dimeric forms. FEBS J. 2010, 277, 1967–1978.