1. Recent Advances using PDE-based and AI-powered Systems

To indirectly support the concept of the two-week predictability limit, the saturation time has been employed as a measure across various time scales for predictability estimates. However, instances of saturation times exceeding two weeks have been documented (Magnusson and Kallen 2013 [1]; Zagar and Szunyogh 2020 [2]). For instance, produced by the extended version of the Lorenz 1965 model (Lorenz 1965) [3], Figure 1 of Krishnamurthy (2019) [4] displayed a saturation time of about 100 days.

Recent studies have also reported reasonable predictions at time scales longer than two weeks (e.g., Liu et al. 2009 [5]; Shen et al. 2010, 2011 [6, 7]; Judt 2018 [8]; Krishnamurthy 2019 [4]). For example, applying ensemble forecasts to simulate stratospheric sudden warming (Mukougawa and Hirooka 2004) [9], Mukougawa et al. (2005) [10] reported a lead time of more than two weeks. By examining the dependence of predictability on regions, Judt (2020) [11] suggested that the tropics have longer predictability than the middle latitudes and polar regions (tropics > 20 days). Using an atmosphere–ocean coupled model (or a stand-alone model), Mishra et al. (2021) [12] reported a predictability limit of 22 days (or 20 days) for Indian monsoon rainfall.

Compared to PDE-physics-based methods, machine learning (ML), or more broadly, artificial intelligence (AI) methods have shown promise in improving weather predictions (Weyn et al. 2019, 2020, 2021 [13-15]; Rasp and Thuerey 2021 [16]; Pathak et al. 2022 [17]; Bi et al. 2023 [18]; Bonev et al. 2023 [19]; Chen, Han, et al. 2023 [20]; Chen, Zhong et al. 2023 [21]; Nguyen. et al. 2023 [22]; Lam et al. 2023 [23]; Selz and Craig 2023 [24]; Watt-Meyer et al. 2023 [25]; Bach et al. 2024 [26]; Bouallègue et al. 2024 [27]; Li et al. 2024 [28]). As shown in Table 1, these AI-powered models were trained using the ERA5 reanalysis dataset (Hersbach et al. 2018, 2020) [29, 30] and CMIP6 data (Eyring et al. 2016 [31]) and assessed using various metrics including RMSE, ACC, Continuous Ranked Probability Score (CRPS), Temporal Anomaly Correlation Coefficient (TCC), Ranked Probability Skill Score (RPSS), Brier Skill Score (BSS), and bivariate correlation (COR).

As summarized in Table 1, by applying deep convolutional neural networks (CNNs), Weyn et al. (2019) [13] reported lead times of 14 days. More importantly, recent advances in AI technology, particularly transformer technology (e.g., Vaswani et al. 2017) [32] and its variants, including the “vision transformer” (Dosovitskiy et al. 2020 [33]), have offered significant opportunities to reduce the cost of weather predictions and revisit the predictability limit. Table 1 lists major AI-powered systems, most of which were published in 2023 and 2024 following the widespread recognition of transformer technology due to its major application in ChatGPT. Among the listed AI-powered systems, as compared to PDE-physics-based systems, all produced comparable or slightly better predictions for conventional short-term forecasts (3–14 days). Three studies have attempted to perform simulations at subseasonal or larger scales. Among the three studies, the ClimX system was reported in a conference article. The enhanced Fu-Xi system (and its base version) was documented in a preprint article (and journal article). In the 3rd study, the hybrid dynamical and data-driven approach was applied by Bach et al. (2024, PNAS) [26] to successively demonstrate the potential for improving subseasonal monsoon prediction. As derived from their study, Figure 1 displays a correlation above 0.5 over a 46-day period in two predictions.

Table 1. A list of major AI-powered systems.

Further studies utilizing AI-powered systems include, but are not limited to, works by Bodnar et al. (2024) [34], Kochhov et al. (2024) [35], Lang et al. (2024) [36], Mardani et al. (2023) [37], Price et al. (2024) [38], Vonich and Hakim (2024) [39], and Wu and Xue (2024) [40], all demonstrating the swift advancements facilitated by AI. Notably, Wu and Xue (2024) [40] conducted a thorough review of AI-based models from a developmental viewpoint. Lang et al. (2024) [36] described the ECMWF’s AI-based system. Kochhov et al. (2024) [35] introduced a novel model that integrates PDEs and ML to generate ensemble weather forecasts more accurately, as assessed by CRPS, than the existing ECMWF model. Vonich and Hakim (2024) [39] reported a predictability of 23 days for the Pacific Northwest heatwave.

Although the above systems have not yet established a new predictability horizon, our suggestion, viewing the two-week limit as a predictability hypothesis, makes it easier for scientists to understand why the above promising results with specific weather systems are possible and encourage attempts for proving or disproving the hypothetical two-week predictability limit. More importantly, AI-powered methods provide alternative, cost-effective approaches.

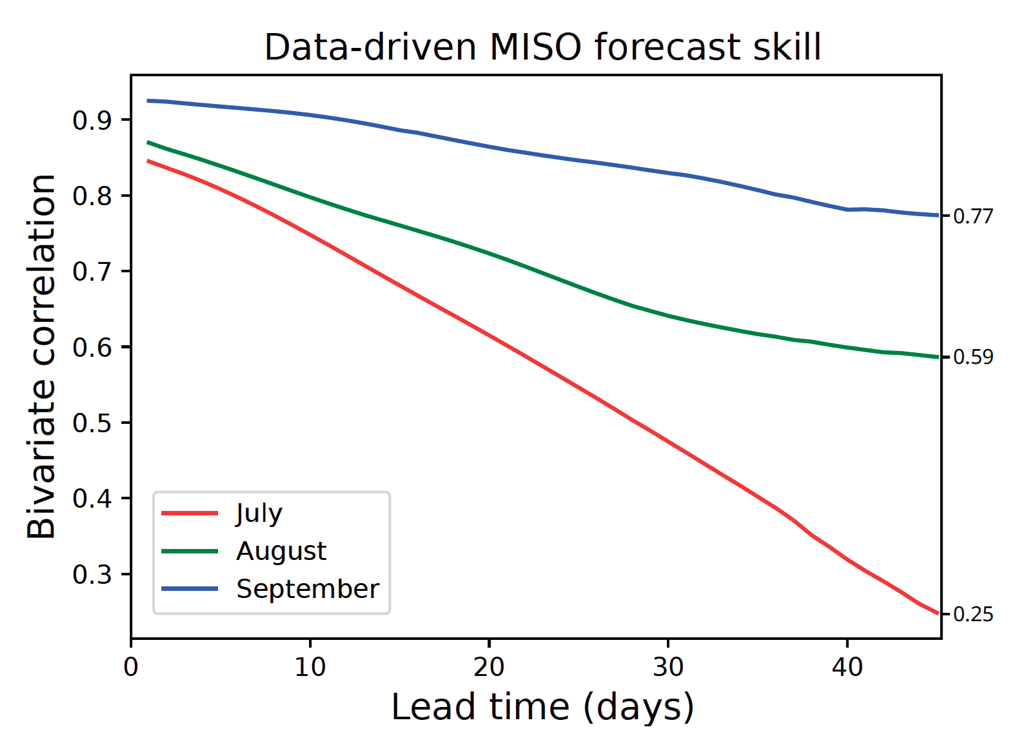Figure 1. Time-varying correlation coefficient between predicted and observed monsoon intraseasonal oscillation (MISO) modes, for forecasts initiated on the 1st of July, August, and September, spanning the years 2008 to 2016. (Bach et al. (2024) [26])

2. A View of Distinct Predictability Using a Generalized Lorenz Model

By guiding the choice of numerical results from real-world models, the concept of Lorenz’s chaos, characterized by aperiodic features and instability, indeed, indirectly influenced the establishment of the two-week predictability limit. Specifically, the key characteristics of Lorenz’s 1963 and 1969 models provide evidence for the existence of a predictability limit. However, it is important to note that the underlying mechanisms or sensitivities that lead to finite predictability differ between these models (e.g., as discussed in Shen et al. 2021a [41], 2022a, c [42, 43]).

Lorenz’s 1963 model is characterized by its limited scale and chaotic nature, while the Lorenz 1969 model is closure-based, physically multiscale, mathematically linear, and numerically ill-conditioned. Furthermore, as elaborated on in Section 3.1.2 of Shen et al. 2022a [42], the Lorenz 1969 ill-conditioned system tends to easily capture numerical instability.

As discussed by Shen et al. (2023a) [44] and Shen (2023a) [45], most of Lorenz’s models did not incorporate spatial and time-varying “backgrounds.” For example, the Lorenz 1963 model utilized time-independent parameters and the Lorenz 1969 model applied a time-independent kinetic energy spectrum, as well as assumed homogeneity and isotropy. To address this limitation, we employed a generalized Lorenz model (Shen 2019a [46]; Shen et al. 2019 [47]) and applied a time-varying parameter that emulates the impact of slowly varying variables.

As illustrated by Shen et al. (2021a) [41], the Rayleigh parameter is set to a periodic function of time that allows different types of solutions; equations for the generalized Lorenz model are additionally provided in the Supplementary Materials of Shen et al. (2021a) [41]. Our findings revealed the coexistence of chaotic and non-chaotic properties, including nonlinear oscillations (i.e., limit cycle solutions), and the coexistence of rapidly and slowly varying solutions (Shen et al. 2021a) [41]. Such findings challenge the conventional view that the system is solely chaotic and suggest a revised view on the dual nature of chaos and order with coexisting short-term and long-term predictability. For example, the appearance of the theoretical nonlinear oscillations could provide a support to the existence of oscillations such as monsoon intraseasonal oscillation (MISO) for better predictability, as discussed above in Figure 1 (Bach et al. 2004) [26]. The concept of attractor coexistence also helped us uncover regional dependencies, such as blocking patterns and seasonal variations.

Furthermore, as depicted in Figure 5 of Shen et al. (2022c) [43], our generalized Lorenz model results suggest the possibility of regime transitions between regular and chaotic solutions. Both the previously mentioned studies and recent research (e.g., Zeng 2023) [48] support Lorenz’s 1997 updated perspective, suggesting a possibility for the coexisting long predictability of ENSO and short-term predictability (i.e., 2-week predictability, when applicable).

3. Proposed Future Research Directions

The “Next Generation Earth System Prediction: Strategies for Subseasonal to Seasonal Forecasts” report by the National Academy of Sciences (2016) [49] underscores the societal benefits of the broad implementation of subseasonal to seasonal (S2S) forecasts, which provide predictions ranging from two weeks to twelve months ahead. The report projects that S2S forecasts will become as commonplace as daily weather reports, playing a vital role in sectors such as agriculture, water management, and public health. These forecasts are pivotal in reducing risks associated with extreme weather events, thereby safeguarding lives and reducing economic losses. The report points out a significant disparity in the support for S2S forecasts compared to immediate weather predictions and long-term climate projections, and it identifies substantial challenges, including the need for forecasts that align more closely with the specific temporal and spatial requirements of users. It calls for collaborative efforts between physical and social scientists to enhance the applicability of S2S forecasts across various decision-making scenarios. Concurrently, as mentioned earlier, recent advancements in AI and ML have produced promising forecasts that extend beyond two weeks (refer to Figure 1) and have improved forecast customization through techniques such as downscaling, as demonstrated by Mardani et al. (2023) [37], highlighting the critical role of data scientists in this field.

Building on the insights from this report and previous research, we are optimistic that ongoing innovations in both practical and theoretical modeling, augmented by artificial intelligence, will continually enhance our understanding and prediction of weather phenomena. These advancements are especially beneficial for investigating pivotal phenomena such as the butterfly effect (model sensitivities), multiscale interactions, and multistability, which encompass feedback from numerically or physically small-scale processes, modulation by large-scale systems, and predictability that varies with different types of weather systems. To advance these efforts, we propose a series of research areas that would benefit from an integrated approach combining PDE-based methods and AI-enhanced techniques:

1. Enhancing numerical methods by implementing variable time steps.
2. Fusing AI with ensemble forecasting to refine predictive accuracy.
3. Measuring the the sensitivity dependence on initial conditions (SDIC) –i.e. the butterfly effect – and chaotic behaviors in AI-driven systems.
4. Improving spatial and/or temporal resolution through AI-powered downscaling.
5. Expanding the functionality of AI models by integrating non-forecast variables.
6. Discovering multiscale processes via singular value analysis of query, key, and value matrices.
7. Crafting conceptual models to deepen the understanding of predictability.
8. Reevaluating the boundaries of predictability horizons.
9. Evaluating how the temporal extent of reanalysis data affects the precision of climate projections
10. Investigating AI-based model hallucinations and their linkage to sensitive dependence on initial conditions.

For additional details, please refer to Shen et al. (2024) [50].

4. Concluding Remarks

To provide a clearer perspective on the two-week predictability limit, we have conducted a systematic study of Lorenz’s models and predictability, collectively suggesting the following statement:

“Much like Moore’s Law in the realm of computing, the predictability limit hypothesis, specifically the two-week predictability limit, is an empirical association based on practical modeling and idealized chaotic modeling from the 1960s. It stands as a limited set of observed findings and as a reasonable extrapolation from early modeling results during the 1960s, rather than constituting fundamental physics.”

The above, referred to as the Predictability Limit Hypothesis, summarizes the historical context of predictability research, encompassing real-world, theoretical models, and other approaches from the 1960s. Our reevaluation highlights quantitative estimates of two-week predictability using the Mintz–Arakawa model, as well as qualitative, finite predictability within Lorenz’s 1963 and 1969 models, under the leadership of Charney et al. This concept also aligns with Lorenz’s evolved perspective on predictability limits in the 1990s and 2000s.

Our studies, combined with our previous research (e.g., Shen et al. 2021a; 2022c [41, 43]), highlight cumulative advancements in both PDE-physics-based and AI-powered systems since the 1960s, which have shown promising results in long-term simulations. Although these simulations extend beyond the traditional two-week limit, they do not contradict the Predictability Limit Hypothesis based on 1960s models. This new concept helps explain why the practical capabilities of current models are still consistent with the major findings of finite predictability within Lorenz’s theoretical models.

Recognizing that weather prediction is a combined boundary-initial value problem imposes constraints on temporal changes. This concept can also extend to examine the predictability of seasonal, yearly, decadal, and longer climate predictions. The feasibility of this approach was illustrated by developing a unified weather and climate model, which led to successful short-term weather predictions in the early 2000s (e.g., Lin et al. 2003 [51]; Atlas et al. 2005 [52]; Shen et al. 2006a, b, 2010, 2011 [53, 54, 6, 7]). In comparison, AI-powered systems trained over several decades using ERA5 reanalysis and/or CMIP6 data can be viewed as weather-climate unified systems. Both weather and climate forecasts predict changes in the state of variables such as temperature and precipitation, then compute their averages over different time scales. With weather, this can involve hourly or daily averages, while climate focuses on yearly and longer-term statistics. Both forecasts essentially use the same mathematical framework (with climate involving more nonlinear interactions) within PDE-physics-based or AI-powered systems. The question remains whether and how the concepts discussed for short time scales can extend to climate prediction at longer time scales.

References

1. Magnusson, L.; Källén, E. Factors Influencing Skill Improvements in the ECMWF Forecasting System. Weather. Rev.2013, 141, 3142–3153.
2. Zagar, N.; Szunyogh, I. Comments on “What Is the Predictability Limit of Midlatitude Weather?”. Atmospheric Sci.2020, 77, 781–785.
3. Lorenz, N. A study of the predictability of a 28-variable atmospheric model. Tellu 1965, 17, 321–333.
4. Krishnamurthy, Predictability of weather and climate. Earth Space Sci. 2019, 6, 1043–1056. https://doi.org/10.1029/2019EA000586.
5. Liu, -L.; Sassi, F.; Garcia, R.R. Error Growth in a Whole Atmosphere Climate Model. J. Atmos. Sci. 2009, 66, 173–186.
6. Shen, -W.; Tao, W.-K.; Wu, M.-L. African Easterly Waves in 30-day High-resolution Global Simulations: A Case Study during the 2006 NAMMA Period. Geophys. Res. Lett. 2010, 37, L18803. https://doi.org/10.1029/2010GL044355.
7. Shen, -W.; Tao, W.-K.; Green, B. Coupling Advanced Modeling and Visualization to Improve High-Impact Tropical Weather Prediction (CAMVis). IEEE Comput. Sci. Eng. (CiSE) 2011, 13, 56–67. https://doi.org/10.1109/MCSE.2010.141.
8. Judt, Insights into Atmospheric Predictability through Global Convection-Permitting Model Simulations. J. Atmos. Sci. 2018, 75, 1477–1497.
9. Mukougawa, ; Hirooka, T. Predictability of stratospheric sudden warming: A case study for 1998/99 winter. Mon. Weather Rev. 2004, 132, 1764–1776.
10. Mukougawa, ; Sakai, H.; Hirooka, T. High Sensitivity to the Initial Condition for the Prediction of Stratospheric Sudden Warming. Geophys. Res. Lett. 2005, 32, L17806.
11. Judt, Atmospheric predictability of the tropics, middle latitudes, and polar regions explored through global storm-resolving simulations. J. Atmos. Sci. 2020, 77, 257–276. https://doi.org/10.1175/JAS-D-19-0116.1.
12. Mishra, K.; Dwivedi, S.; Di Sante, F. Performance of the RegCM-MITgcm Coupled Regional Model in Simulating the Indian Summer Monsoon Rainfall. Pure Appl. Geophys. 2021, 178, 603–617.
13. Weyn, A.; Durran, D.R.; Caruana, R. Can Machines Learn to Predict Weather? Using Deep Learning to Predict Gridded 500-hPa Geopotential Height from Historical Weather Data. J. Adv. Model. Earth Syst. 2019, 11, 2680–2693.
14. Weyn, A.; Durran, D.R.; Caruana, R. Improving data-driven global weather prediction using deep convolutional neural networks on a cubed sphere. J. Adv. Model. Earth Syst. 2020, 12, e2020MS002109.
15. Weyn, ; Durran, D.; Caruana, R.; Cresswell-Clay, N. Sub-seasonal forecasting with a large ensemble of deeplearning weather prediction models. J. Adv. Model. Earth Syst. 2021, 13, e2021MS002502.
16. Rasp, ; Thuerey, N. Data-driven medium-range weather prediction with a Resnet pretrained on climate simulations: A new model for WeatherBench. J. Adv. Model. Earth Syst. 2021, 13, e2020MS002405. https://doi.org/10.1029/2020MS002405.
17. Pathak, ; Subramanian, S.; Harrington, P.; Raja, S.; Chattopadhyay, A.; Mardani, M.; Kurth, T.; Hall, D.; Li, Z.; Azizzadenesheli, K.; et al. Fourcastnet: A Global Data-Driven High-Resolution Weather Model Using Adaptive Fourier Neural Operators. arXiv 2022, arXiv:2202.11214.
18. Bi, ; Xie, L.; Zhang, H.; Chen, X.; Gu, X.; Tian, Q. Accurate medium-range global weather forecasting with 3D neural networks. Nature 2023, 619, 533–538. https://doi.org/10.1038/s41586-023-06185-3.
19. Bonev, ; Kurth, T.; Hundt, C.; Pathak, J.; Baust, M.; Kashinath, K.; Anandkumar, A. Spherical Fourier Neural Operators: Learning Stable Dynamics on the Sphere. arXiv 2023, arXiv.2306.03838. https://doi.org/10.48550/arXiv.2306.03838.
20. Chen, ; Han, T.; Gong, J.; Bai, L.; Ling, F.; Luo, J.J.; Chen, X.; Ma, L.; Zhang, T.; Su, R.; et al. FengWu: Pushing The Skillful Global Medium-Range Weather Forecast Beyond 10 Days Lead. arXiv 2023, arXiv:2304.02948.
21. Chen, ; Zhong, X.; Zhang, F.; Cheng, Y.; Xu, Y.; Qi, Y.; Li, H. FuXi: A cascade machine learning forecasting system for15-day global weather forecast. NPJ Clim. Atmos. Sci. 2023, 6, 190. https://doi.org/10.1038/s41612-023-00512-1.
22. Nguyen, ; Brandstetter, J.; Kapoor, A.; Gupta, J.K.; Grover, A. Climax: A Foundation Model for Weather and Climate. arXiv 2023, arXiv:2301.10343.
23. Lam, ; Sanchez-Gonzalez, A.; Willson, M.; Wirnsberger, P.; Fortunato, M.; Alet, F.; Ravuri, S.; Ewalds, T.; Eaton-Rosen, Z.; Hu, W.; et al. Learning skillful medium-range global weather forecasting. Science 2023, 382, 1416–1421. https://doi.org/10.1126/science.adi2336.
24. Selz, ; Craig, G.C. Can artificial intelligence-based weather prediction models simulate the butterfly effect? Geophys. Res. Lett. 2023, 50, e2023GL105747. https://doi.org/10.1029/2023GL105747.
25. Watt-Meyer, ; Dresdner, G.; McGibbon, J.; Clark, S.K.; Henn, B.; Duncan, J.; Brenowitz, N.D.; Kashinath, K.; Pritchard, M.S.; Bonev, B.; et al. ACE: A fast, skillful learned global atmospheric model for climate prediction. arXiv 2023, arXiv:2310.02074v1. https://doi.org/10.48550/arXiv.2310.02074.
26. Bach, ; Krishnamurthy, V.; Mote, S.; Shukla, J.; Sharma, A.S.; Kalnay, E.; Ghil, M. Improved subseasonal prediction of South Asian monsoon rainfall using data-driven forecasts of oscillatory modes. Proc. Natl. Acad. Sci. USA 2024, 121, e2312573121. https://doi.org/10.1073/pnas.2312573121.
27. Bouallègue, B.; Clare, M.C.A.; Magnusson, L.; Gascón, E.; Maier-Gerber, M.; Janoušek, M.; Rodwell, M.; Pinault, F.; Dramsch, J.S.; Lang, S.T.K.; et al. The rise of data-driven weather forecasting: A first statistical assessment of machine learning-based weather forecasts in an operational-like context. Bull. Am. Meteorol. Soc. 2024, 105, E864–E883. https://doi.org/10.1175/BAMS-D-23-0162.1.
28. Li, ; Chen, L.; Zhong, X.; Wu, J.; Chen, D.; Xie, S.P.; Chao, Q.; Lin, C.; Hu, Z.; Lu, B.; et al. A machine learning model that outperforms conventional global subseasonal forecast models. Phys. Sci. 2024, under review. https://doi.org/10.21203/rs.3.rs-3776375/v1.
29. Hersbach, ; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 hourly data on single levels from 1979 to present. Copernic. Clim. Change Serv. (C3S) Clim. Data Store (CDS) 2018, 10.
30. Hersbach, ; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049.
31. Eyring, ; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the coupled model intercomparison project phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 2016, 9, 1937–1958.
32. Vaswani, ; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. “Attention Is All You Need”. Advances in Neural Information Processing Systems. 30. Curran Associates, Inc. 2017. Available online: https://proceedings.neurips.cc/paper/2017/file/3f5ee243547dee91fbd053c1c4a845aa-Paper.pdf (accessed on May 1, 2024).
33. Dosovitskiy, ; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. arXiv 2020, arXiv:2010.11929. https://doi.org/10.48550/arXiv.2010.11929.
34. Bodnar, ; Bruinsma, W.P.; Lucic, A.; Stanley, M.; Brandstetter, J.; Garvan, P.; Riechert, M.; Weyn, J.; Dong, H.; Vaughan, A.; et al. Aurora: A Foundation Model of the Atmosphere. arXiv 2024, arXiv:2405.13063. https://doi.org/10.48550/arXiv.2405.13063.
35. Kochkov, ; Yuval, J.; Langmore, I.; Norgaard, P.; Smith, J.; Mooers, G.; Lottes, J.; Rasp, S.; Düben, P.; Klöwer, M.; et al. Neural General Circulation Models for Weather and Climate. arXiv 2024, arXiv:2311.07222. https://doi.org/10.48550/arXiv.2311.07222.
36. Lang, ; Alexe, M.; Chantry, M.; Dramsch, J.; Pinault, F.; Raoult, B.; Clare, M.C.; Lessig, C.; Maier-Gerber, M.; Magnusson, L.; et al. AIFS—ECMWF’S Data-Driven Forecasting System. arXiv 2024, arXiv:2406.01465. https://doi.org/10.48550/arXiv.2406.01465.
37. Mardani, ; Brenowitz, N.; Cohen, Y.; Pathak, J.; Chen, C.Y.; Liu, C.C.; Vahdat, A.; Kashinath, K.; Kautz, J.; Pritchard, M. Residual Diffusion Modeling for Km-scale Atmospheric Downscaling. arXiv 2023, arXiv:2309.15214. https://doi.org/10.48550/arXiv.2309.15214.
38. Price, ; Sanchez-Gonzalez, A.; Alet, F.; Ewalds, T.; El-Kadi, A.; Stott, J.; Mohamed, S.; Battaglia, P.; Lam, R.; Willson, M. 2024: GenCast: Diffusion-based ensemble forecasting for medium-range weather. arXiv 2023, arXiv:2312.15796. https://doi.org/10.48550/arXiv.2312.15796.
39. Vonich, T.; Hakim, G.J. Predictability Limit of the 2021 Pacific Northwest Heatwave from Deep-Learning Sensitivity Analysis. arXiv 2024, arXiv:2406.05019. https://doi.org/10.48550/arXiv.2406.05019.
40. Wu, ; Xue, W. Data-Driven Weather Forecasting and Climate Modeling from the Perspective of Development. Atmosphere 2024, 15, 689. https://doi.org/10.3390/atmos15060689.
41. Shen, -W.; Pielke, R.A., Sr.; Zeng, X.; Baik, J.-J.; Faghih-Naini, S.; Cui, J.; Atlas, R. Is Weather Chaotic? Coexistence of Chaos and Order within a Generalized Lorenz Model. Bull. Am. Meteorol. Soc. 2021, 2, E148–E158. https://doi.org/10.1175/BAMS-D-19-0165.1.
42. Shen, -W.; Pielke, R.A., Sr.; Zeng, X. One Saddle Point and Two Types of Sensitivities within the Lorenz 1963 and 1969 Models. Atmosphere 2022a, 13, 753. https://doi.org/10.3390/atmos13050753.
43. Shen, -W.; Pielke, R.A., Sr.; Zeng, X.; Cui, J.; Faghih-Naini, S.; Paxson, W.; Kesarkar, A.; Zeng, X.; Atlas, R. The Dual Nature of Chaos and Order in the Atmosphere. Atmosphere 2022c, 13, 1892. https://doi.org/10.3390/atmos13111892.
44. Shen, -W.; Pielke, R.A., Sr.; Zeng, X. 50th Anniversary of the Metaphorical Butterfly Effect since Lorenz (1972): Special Issue on Multistability, Multiscale Predictability, and Sensitivity in Numerical Models. Atmosphere 2023a, 14, 1279. https://doi.org/10.3390/atmos14081279.
45. Shen, -W. A Review of Lorenz’s Models from 1960 to 2008. Int. J. Bifurc. Chaos 2023, 33, 2330024. https://doi.org/10.1142/S0218127423300240.
46. Shen, B.-W Aggregated negative feedback in a generalized Lorenz model. J. Bifurc. Chaos2019, 29, 1950037.
47. Shen, -W.; Reyes, T.; Faghih-Naini, S. Coexistence of Chaotic and Non-Chaotic Orbits in a New Nine-Dimensional Lorenz Model. In 11th Chaotic Modeling and Simulation International Conference. CHAOS 2018; Skiadas, C., Lubashevsky, I., Eds.; Springer Proceedings in Complexity; Springer: Cham, Switzerland, 2019. https://doi.org/10.1007/978-3-030-15297-0_22.
48. Zeng, Atmospheric Instability and Its Associated Oscillations in the Tropics. Atmosphere 2023, 14, 433. https://doi.org/10.3390/atmos14030433.
49. National Academies of Sciences, Engineering, and Medicine. Next Generation Earth System Prediction: Strategies for Subseasonal to Seasonal Forecasts; The National Academies Press: Washington, DC, USA, 2016. https://doi.org/10.17226/21873.
50. Shen, -W.; Pielke, R.A., Sr.; Zeng, X. Special Issue Theme Topic: “Revisiting Butterfly Effect, Multiscale Dynamics, and Predictability Using Ai-Enhanced Modeling Framework (AEMF) and Chaos Theory”. 2024. https://doi.org/10.13140/RG.2.2.33483.20003. Available online: https://www.mdpi.com/topics/B9N0115Q3E (accessed on May 1, 2024).
51. Lin, -J.; Shen, B.-W.; Putman, W.P.; Chern, J.-D. Application of the high-resolution finite-volume NASA/NCAR Climate Model for Medium-Range Weather Prediction Experiments. In Proceedings of the EGS-AGU-EUG Joint Assembly, Nice, France, 6–11 April 2003.
52. Atlas, ; Reale, O.; Shen, B.; Lin, S.; Chern, J.; Putman, W.; Lee, T.; Yeh, K.; Bosilovich, M.; Radakovich, J. Hurricane forecasting with the high-resolution NASA finite-volume General Circulation Model. Geophys. Res. Lett. 2005, 32, L03801. https://doi.org/10.1029/2004GL021513.
53. Shen, B.-W.; Atlas, ; Oreale, O.; Lin, S.-J.; Chern, J.-D.; Chang, J.; Henze, C.; Li, J.-L. Hurricane Forecasts with a Global Mesoscale-Resolving Model: Preliminary Results with Hurricane Katrina (2005). Geophys. Res. Lett. 2006, 33, L13813. https://doi.org/10.1029/2006GL026143.
54. Shen, -W.; Atlas, R.; Chern, J.-D.; Reale, O.; Lin, S.-J.; Lee, T.; Chang, J. The 0.125 degree Finite Volume General Mesoscale Circulation Model: Preliminary simulations of mesoscale vortices. Geophys. Res. Lett. 2006, 33, L05801. https://doi.org/10.1029/2005GL024594.