In the face of an increasingly high-demand environment for outpatients, achieving a balance between allocation of limited medical resources and patient satisfaction has considerable social and economic benefits. Therefore, appointment scheduling (AS) system operation is used in clinics and hospitals, and its operation optimization research is of great significance.
- appointment scheduling (AS)
- optimization algorithm
- healthcare
1. Introduction
2. System Structure of AS
2.1. AS Characteristics
The scheduling of appointments within outpatient departments stands as an extensively investigated subject, playing a pivotal role in facilitating the efficient utilization of clinical services. It is a topic that demands in-depth research, given its significance in ensuring timely access to high-quality care for patients. In outpatient services, a central issue for scheduling staff is how to allocate available time slots for patients, thereby reducing patient delays and physician availability or additional time [26,27][17][18]. The role of appointment scheduling systems in optimizing quality healthcare has been recognized as a challenging problem [28][19]. Appointment scheduling systems are a well-positioned and practical research area. Unlike the traditional way of registering for appointments, it avoids crowd gathering as well as the unknown nature of patient scheduling, and greatly improves the services’ efficiency, which is an emerging field of research within healthcare [29,30,31][20][21][22]. The attributes of ASs are primarily evident in two aspects:-
Uncertainty AS performance;
- 2.
-
ASs can be extended to represent other industries.
2.2. System Structure of AS
The prerequisite for building an AS system is to be familiar with the patient consultation process, as we all know, anyone who wants to consult needs to arrive at the hospital outpatient clinic as early as possible, and then go to the registration desk to obtain a number (even if you use the online advance booking needs to be in accordance with the booking time to report to the queue and wait). After receiving your number, you will wait in the designated viewing area and meet with the doctor when you are called. After the consultation, the patient may need to undergo further tests and return to the queue to consult with the doctor again after receiving the results [41][32]. Figure 1 illustrates the structure of the process for the patient’s outpatient consultation in a clinical setting. The AS system design is viewed as a range of decision-making hierarchies, including appointment rules, classification of patients, and adjustments for reducing the disruptive effect of no-shows, walk-ins, and emergency patients [42][33].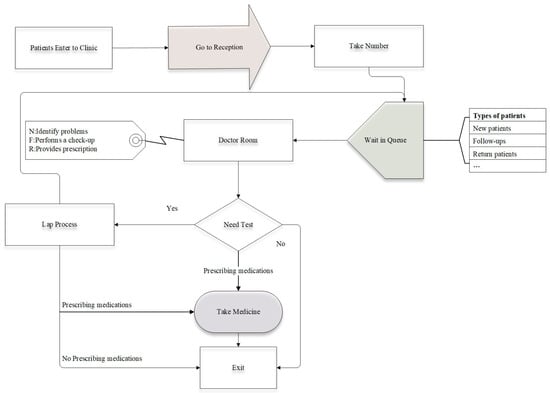 Figure 1.The flow structure of the patient in the hospitals.
Figure 1.The flow structure of the patient in the hospitals.2.2.1. Appointment Rules
AS system operation optimization typically improves healthcare system performance by designing AS rules. These regulations describe the duration of each appointment interval and the number of patients (block size) to be accommodated during that interval. By utilizing various permutations of fixed and variable appointment interval lengths, several innovative rules have been developed to make the operation of the system more responsive to actual consultation needs [17][34]. The appointment rules of the AS system are expressed in terms of block-size (𝑛𝑖: the number of patients assigned per block 𝑖), begin-block (𝑛1:patients assigned the same appointments at the session’s outset), and appointment interval (𝑎𝑖: the interval between two consecutive appointments). The block size and the scheduling interval can be fixed or variable, so the reservation rules composed by the combination of any of its three variables (𝑛𝑖,𝑛1,𝑎𝑖 ) [43][35].1. Fixed-interval rules.-
Fixed-interval rules.
The fixed-interval rule refers to equal intervals throughout the consultation. The intervals between the first patient and the subsequent patient and between every two subsequent patients are fixed, i.e., ai is constant. There are some differences in the other two variables under the fixed-interval rule. Simply, the IBFI (individual-block/fixed-interval rule) assigns individual appointments to every patient with equal intervals throughout the consultation, meaning that 𝑛i=1,𝑛1=1[44] [36]. Considering the patient’s late arrival or no-show, it is possible to increase the number of appointments at the beginning of the meeting for the same time patient refers to n1 > 1. Avoiding the phenomenon of doctor’s idleness improves the efficiency of healthcare workers. Bailey et al. [45,46][37][38] proposed an individual-block system assigning two patients at the session’s start and scheduling the rest at intervals matching the mean consultation time. This highlights the need for thorough research into outpatient appointment scheduling (𝑛1=2,𝑛𝑖=1 ).The multiple-block/fixed-interval rule can be interpreted as assigning m patients to the appointment slot with a constant appointment interval. The multiple-block rule performs better when the consultation time is shorter, and the rise in patient numbers in the same appointment time slot allows for more flexibility in the physician’s and patient’s time. Soriano et al. [47][39] studied a system in which patients are scheduled in pairs, with intervals set at twice the mean consultation time. In fact, block-size can also be variable; the rules allow variations in block sizes throughout the clinic session.- 2.
-
Variable-interval rules.
-
The “offset” rule.
 where Ti is the planned time for client i appointment, as is the standard time for s, and 𝜎 is variability in service time. The parameters 𝐾 , 𝑘1,𝑘2 are the early breakpoints, delay breakpoints and the multipliers. (𝑘1/𝑘2 ) controls the earliness rate imposed on the first 𝐾 patients and the rate of lateness imposed on the remaining patients.
where Ti is the planned time for client i appointment, as is the standard time for s, and 𝜎 is variability in service time. The parameters 𝐾 , 𝑘1,𝑘2 are the early breakpoints, delay breakpoints and the multipliers. (𝑘1/𝑘2 ) controls the earliness rate imposed on the first 𝐾 patients and the rate of lateness imposed on the remaining patients.-
The “dome” appointment rule.
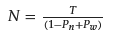 In this formula, 𝑃𝑛 is that a patient fails to attend and 𝑃𝑤 is the probability of coming without an appointment.
The appointment times are determined through a two-step process employing the subsequent formula:
In this formula, 𝑃𝑛 is that a patient fails to attend and 𝑃𝑤 is the probability of coming without an appointment.
The appointment times are determined through a two-step process employing the subsequent formula:
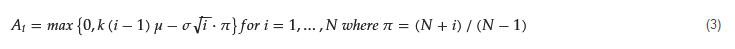 In this formula, 𝐴𝑖 is the patient 𝑖’s scheduled time, with the mean duration of service μ, and variability in service time 𝜎. The k controls the appointment intervals for different appointment rules by setting different values. π is a parameter utilized to establish a pattern resembling a “dome” in the appointment intervals.
In this formula, 𝐴𝑖 is the patient 𝑖’s scheduled time, with the mean duration of service μ, and variability in service time 𝜎. The k controls the appointment intervals for different appointment rules by setting different values. π is a parameter utilized to establish a pattern resembling a “dome” in the appointment intervals.
 In Equation (4), 𝐶𝑣 is the coefficient of variation; and CR is the ratio of the cost of the doctor’s time to that of the patients’ time.
Considering the combined impact of no-shows and walk-ins on the consultation durations, the updated formulas for the mean and variance are shown:
In Equation (4), 𝐶𝑣 is the coefficient of variation; and CR is the ratio of the cost of the doctor’s time to that of the patients’ time.
Considering the combined impact of no-shows and walk-ins on the consultation durations, the updated formulas for the mean and variance are shown:

-
The “plateau-dome” appointment rule.
- The “plateau-dome” appointment rule.
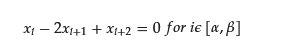 In this formula, 𝑥𝑖 is the appointment time, and 𝛼 and 𝛽 are the appointment slots corresponding to the beginning and end of the plateau portion, respectively.
In this formula, 𝑥𝑖 is the appointment time, and 𝛼 and 𝛽 are the appointment slots corresponding to the beginning and end of the plateau portion, respectively.
2.2.2. Patient Classification
Several investigations have explored the implementation of patient classification (PC) based on the assumption that populations can be categorized into distinct groups. For example, in practice, a prevalent method of classifying patients is according to whether they are new or old who have been examined for a different length of time. This allows patients to be sorted at the time of the appointment, and diversity in consultation duration is combined by patient categorization to adjust the length of the appointment interval according to the characteristics of each group. Most studies are only concerned with the scheduling of patients attending elective appointments [57][49]. Meersman et al. proposed the scheduling horizon involves the time slots for elective and urgent patient categories [58][50], considering the slot allocation of non-elective patients.
2.3. AS System Decision Framework
In AS system design and planning, a range of decisions and planning determine the main structure of the optimization research system. They can be categorized into three types which are strategic, tactical and operational [18][51]. Strategic decisions are the keys in shaping the modeling process and determining the practical applicability of the proposed solutions. Such decisions are usually considered as inputs to the AS system. Tactical decisions aim at determining the system structure. While operational decisions rely on the first two to develop optimization models and rules.2.3.1. Strategic Decisions
Strategic decisions are considered as inputs and are long-term decisions that determine the main structure of the AS system. Robinson et al. [61][52] proposed three main types of access strategies for scheduled patients: traditional, open access, and hybrid. Traditional policies mean all capacity is allocated to pre-scheduled patients, which results in higher no-show rates and longer wait times. Walk-in patients refer to patients who go to the clinic without an appointment during the consultation period. Accepting appointments is a means of mitigating the negative impact of no-shows while increasing modeling complexity due to the dynamic random arrival of non-appointment patients [65][53]. Appointment scheduling methods are categorized into online and offline [66][54]. In the offline method, arranged once all requests have been received, whereas in the online method, patients are promptly scheduled after requests arrive.2.3.2. Tactical Decisions
The primary purpose of approaching the decision problem at the tactical level is to characterize the system to optimize resource utilization and the integrity of the consultation service. For example, in allocating capacity among various groups, the decision should consider factors such as the needs of each patient group, prioritization, probability of absence, revenue per patient group, and patient and physician preferences [68][55], which affect the absence rate and hence the system efficiency. A decrease in the scheduling window results in a reduction of indirect wait time, consequently leading to decrease the absence rate. This enables a more effective use of the clinic’s capacity. Excessive constraints on scheduling windows may result in a reduced patient count, leading to a decline in clinic revenue [69][56]. Issues such as appointment intervals (slots), block size, panel size, etc., are essentially capacity allocation issues as well, affecting tactical-level decisions [70,71,72][57][58][59].2.3.3. Operational Decisions
Operational decisions are associated with plans at the individual-patient level. Rule-based approaches (RBA) and optimization-based approaches (OBA) are used to determine these decisions [68][55]. RBA refers to a set of instructions having associated rules and parameters, but it does not guarantee the realization of optimal performance compared to OBA. Whereas OBA specifies the level of operational decisions, its goal is to attain globally optimal answers for operational decisions [73][60].3. Optimization Framework
3.1. Optimization Objective
3.1.1. Societal Benefit
Many studies in the literature on AS have been devoted to minimizing pathway completion time or maximizing patient satisfaction, which leads to better societal benefits and is the primary goal that hospital management needs to follow. The key performance indicators for minimizing the time to complete all tasks include the average waiting time of patients (WAIT), the average idle time of physicians (IDLE) and the average overtime of physicians (OVER). Dharmadhikari et al. [79][61] used performance metrics of average rewards per patient to assess the effectiveness of the proposed block scheduling strategy with prioritization. Cordier et al. [80][62] developed algorithmic tools to construct one-day schedules and optimize these schedules to optimize the length of patient stay. Nazanin et al. [81][63] conducted case studies for different healthcare settings and selected the most effective scheduling model that fits the case in terms of the balance between three types of metrics related to patient appointment scheduling systems: patient satisfaction, scheduler utilization, and scheduling system cost. Accessibility was a factor of patient satisfaction, measured by the average waiting time before connecting to the dispatch program and the average duration of call.3.1.2. Economic Performance
The appointment scheduling system is a potentially useful tool for reducing health management costs and maximizing medical benefits. Improving system reliability and cost savings are the main ideas of optimization [101,102,103,104][64][65][66][67]. Profit maximization is becoming a major research objective due to the need for cost efficiency and facing budget cuts. Some hospitals maximize profits by rising the number of patients scheduled and maximizing contribution margins. El-Sharo et al. [83][68] modeled an overbooking scheduling model for multi-provider practices to optimize patient overbooking and maximize expected profits.3.1.3. Resource Utilization
With limited healthcare resources, clinics are under tremendous pressure to the increasing demand. Therefore, rational capacity allocation is one of the main goals of AS. Previous papers on outpatient capacity assignment can be divided into two broad categories. One category is where the overall capacity is a constant, the hospital must assign limited medical capacity to various types of patients. For instance, Nguyen et al. [91][69] presented a mixed-integer planning model with the aim of minimizing the maximum demand capacity to plan the demand of outpatient physicians to achieve the service goal of patient appointment lead time. The other category, where the capacity is a variable that needs to be solved in conjunction with the allocation scheduling problem, is categorized into static and dynamic cases. The former means that the decision is made before the session, e.g., Zeng et al. [92][70] investigated the appointment booking problem for heterogeneous patients. The features of optimal scheduling with heterogeneous patients are determined, and a method of local search algorithm is proposed to for finding the locally optimized scheduling. The latter means that appointments are made sequentially, and when a patient calls in, capacity allocation is conducted online, and the hospital needs to decide how much capacity is available for each time slot.3.1.4. Other Objectives
In general, the literature on optimization studies of AS systems covers many aspects, as well as the optimization of objectives through other aspects to obtain better social and economic effects. Savelsbergh et al. [98][71] investigated methods based on optimization and cohorts to SA for patients in a chronic disease management program. The objective was to minimize the overall probability of a patient entering an uncontrolled health state. The approach considers transitions in disease control since the last appointment time and the probability of the patient not attending the appointment. Ozen et al. [72][59] used the probability of demand exceeding capacity as a measure of access capacity. Formulating the problem of minimizing the maximum overflow of a multi-medicine practitioner clinic as a non-linear integration programming problem describes how the frequency of overflow varies from physician to physician and demonstrates how these supply and demand imbalances can be minimized in the long run using real-world data from primary care practices.3.2. Decision Variable
About the optimizing appointment scheduling’s study, the decision variables for optimization show the strategy and actions taken to enhance the objectives [105][72]. Appointment time is one of the common decision variables in the AS problem. Tito et al. [106][73] considered whether patient absence was affected by appointment time using arrival time as the decision variable and investigates a stochastic optimization problem with a random distribution of service times and patient decision-dependent no-show behavior. Solutions are given for different patterns of absenteeism behavior, and it is shown that disrupting the hypothesis of a fixed probability of attendance greatly alters the scheduling scheme.3.3. Constraints
Various optimization decisions about appointment scheduling systems will have different constraints. Optimization studies of ASs are often inseparable from the optimization of operational costs as well as time from the perspective of economic or social benefits [110][74]. Considering the minimum cost of AS operation and the minimum waiting time or the minimum physician overtime time, the constraints consist of appointment sequence, resource capacity, time constraints, etc.4. Optimization Algorithms
Numerous studies have been undertaken to determine the optimal allocation of AS systems to reduce operational and time costs, improve patient satisfaction and system reliability dependability. Various algorithms are applied to the optimization of AS systems, with genetic algorithms (GAs) being the most utilized. For instance, Braune et al. [112][75] proposed a combination of GAs and Monte Carlo simulation to heuristically solve a stochastic optimization model developed for planning the appointment times of healthcare units under uncertain activity durations, allowing to minimize the waiting time of patients while maximizing the use of resources. Fan et al. [113][76] considered patient preferences for highly qualified general practitioners and specialist doctors. By analyzing real data from hospital outpatient clinics, a behavioral pattern was derived in which the patient’s tolerance limit adapted to the expected waiting time. A simulation optimization framework for maximizing clinic benefits and minimizing patient dissatisfaction is proposed. Utilizing multi-objective optimization and a genetic algorithm, a simulation budget allocation approach is integrated to derive an approximate Pareto scheme for joint capacity planning and patient scheduling across multiple servers. In addition, the key to the appointment dilemma is the challenge of solving the multi-objective optimization problem; therefore, many decisions need to be made using a multi-objective evolutionary algorithm. Mohammad et al. [115][77] improved the quality of operational efficiency and healthcare quality by writing a MOPSO algorithm and introducing a MO-PASS architecture. Ali et al. [116][78] investigated a multi-criteria approach in appointment scheduling by WOA. optimization for hospital management quality and patient satisfaction. There are some other methods to solve this problem. Garaix et al. [118][79] proposed a heuristic to calculate the order in which patients receive treatment at outpatient chemotherapy centers called the GRASP algorithm. It optimizes the facility’s closing time and overtime working time. It can reach near-optimal solutions quickly and the performance of the patient-listing strategy is comparable to more complex scheduling strategies.4.1. Genetic Algorithm
Genetic algorithms (GAs) offer an efficient approach to optimizing complex systems. Previous research indicates that many scholars have employed GAs to address optimization problems in the scheduling fields. For example, Squires et al. [124][80] proposed a new genetic algorithm designed for scheduling repetitive transcranial magnetic stimulation (rTMS) appointments. The mentioned algorithm (LSWT-GA) combines a novel survivor selection strategy with heuristic population initialization. The objective of the algorithm is to enhance the operational efficiency of medical centers by optimizing the scheduling of repetitive transcranial magnetic stimulation (rTMS) appointments.4.1.1. Objective Function and Constraint
The primary goal of the initial aim in the experiment is to minimize the job processing time expressed as 𝐶max and aim to minimize weighted flowtime 𝐹𝑤 secondly. The problem can be under the category of minimizing make span in a parallel machine scenario, where job processing times are deterministic, and preemption is not allowed.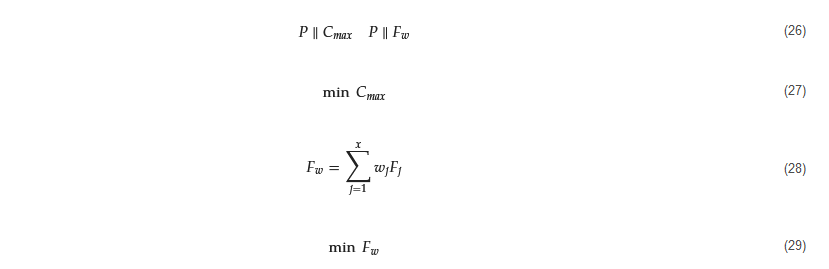 where
where
 In this formula, 𝑃 is a group of patients waiting for a treatment, 𝐹𝑗 denotes the flowtime of patient 𝑃𝑗; 𝐶𝑗 is the time to finish the treatment for 𝑃𝑗 and 𝑟𝑗
is the release time of the job.
In this formula, 𝑃 is a group of patients waiting for a treatment, 𝐹𝑗 denotes the flowtime of patient 𝑃𝑗; 𝐶𝑗 is the time to finish the treatment for 𝑃𝑗 and 𝑟𝑗
is the release time of the job.
4.1.2. Optimization Process
Thise study presents the new genetic algorithm used. Drawing inspiration from evolution, the genetic algorithm relies on natural selection to choose the most suitable chromosomes, as determined by a fitness function, for the reproduction phase of the genetic algorithm. Figure 2 illustrates the flowchart of the optimization algorithm.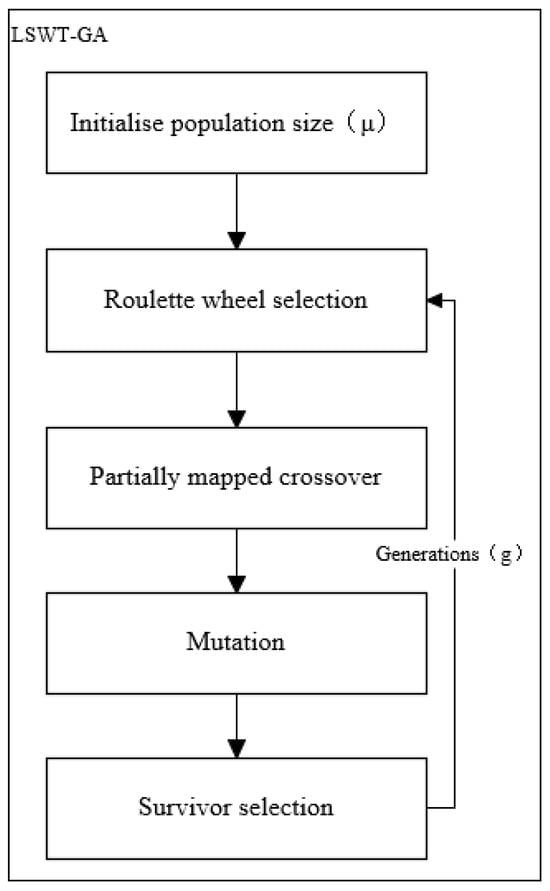 Figure 2.Flowchart of genetic algorithm modules.
Figure 2.Flowchart of genetic algorithm modules.4.2. Whale Optimization Algorithm
The WOA algorithm is a meta-heuristic algorithm designed with both subtlety and character, which is derived from simulating the hunting behavior of humpback whale groups in nature and realizes the purpose of optimizing search through the process of searching, pursuing, and attacking prey by the whale group. The WOA literature has been widely used in solving various of optimization problems, and Ali et al. [116][78] explores the multi-criteria in AS were analyzed using both algorithms, WOA and NSGA techniques. They are computed using various assumptions to meet the requirements and aspects associated with WOA and NSGA.4.2.1. Optimization Model
Scheduling and counseling patients for scheduling to the hospital is the issue discussed. Each hospital section has a varying number of operators to handle distinct operations. Moreover, each capable of providing specific services. In this system, there are n patients, categorized as either emergency or general patients. There are several surgeries for each patient that must be performed in different departments. In addition to this, it may diagnose a patient as an emergency at the time of planning. Emergency patients are usually visited earlier than general patients and are given precedence (fairness). After doing something such as seeing a doctor, the diagnosis depending on the patient’s condition, in which case the patient is referred to an inpatient unit with limited beds.4.2.2. Objective Function
The objective function is to minimize the average total weighted patient time and to reduce dissatisfaction because of increased waiting time for patients.
4.2.3. Constraint
Examination or processing of each patient’s procedure is exclusive in one location on one ward, as shown in the formula below. And for the restriction in a sequencing assured to prevent patients from being assigned to a segment of the surgery when another area is empty, as shown in the Formulas (33) and (34).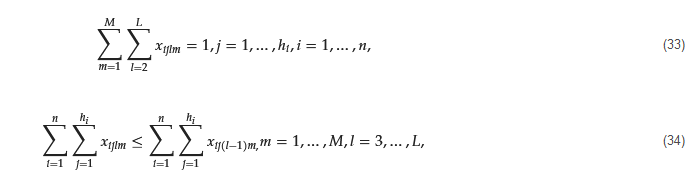 where x is the Appointment System Decision Variables and is equivalent to 1 if the action 𝑂𝑖𝑗 is performed in section 𝑚𝑡ℎ at position 𝑖𝑡ℎ . It is also important to consider the indexes used for appointments, appointment durations, association variables, etc.
where x is the Appointment System Decision Variables and is equivalent to 1 if the action 𝑂𝑖𝑗 is performed in section 𝑚𝑡ℎ at position 𝑖𝑡ℎ . It is also important to consider the indexes used for appointments, appointment durations, association variables, etc.4.2.4. Model Solving
Thise study solves the model by introducing a local search operator to optimize the solution, using the stochastic WOA nature of the meta-heuristic algorithm. The WOA begins with stochastic solutions. Depending on each search factor, the search agent arbitrarily changes according to the optimal solution. The position of the task agent can be updated through two methods. If |A| > 1, a random search agent is chosen; otherwise, the optimal solution is selected. The whale can transition between two types of motions, either spiral or rotational, depending on the p-value. Eventually, the algorithm concludes when it attains a predefined satisfaction criterion, where x* represents the best solution, as shown in Figure 3.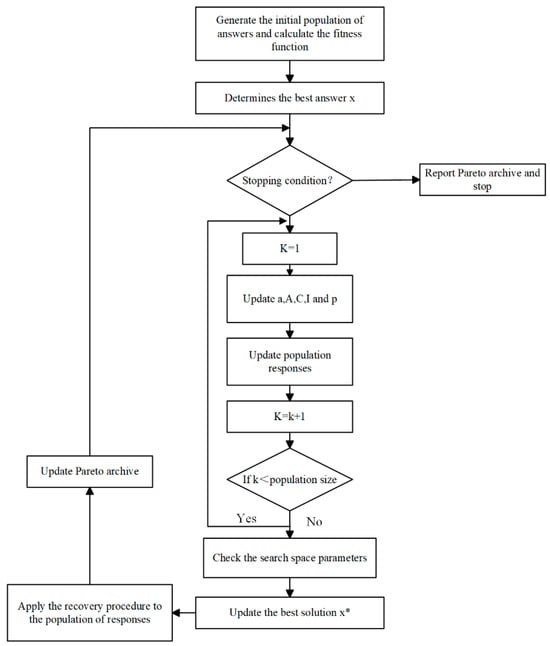 Figure 3. Proposed flowchart for the whale optimization algorithm.
Figure 3. Proposed flowchart for the whale optimization algorithm.4.3. Tabu Search Algorithm
4.3.1. The Integer Programming Model in a Definitive Model
The optimization objective is reducing waiting periods and the cost of completion times to a minimum. Every patient went through three phases of initial admission and surgery and recovery phases of surgery. whereProposed flowchart for the whale optimization algorithm.
whereProposed flowchart for the whale optimization algorithm.4.3. Tabu Search Algorithm
4.3.1. The Integer Programming Model in a Definitive Model
The optimization objective is reducing waiting periods and the cost of completion times to a minimum. Every patient went through three phases of initial admission and surgery and recovery phases of surgery.where𝑞denotes the queue limit,𝛾is the resource capacity content, and𝛽denotes the patient visit or procedure completion time. Meanwhile, patient queue balance as well as resource capacity versus the number of patients to be served are constraints of the appointment system.4.3.2. Algorithm Optimal Progress
The random solution called at the beginning of the algorithm is𝑥0 . And the best-found neighbor solution,. And the best-found neighbor solution,𝑥′ , is named as a pivot. Tabu tenure comes into play to navigate away from local optima throughout the search process. An iterative update of the list is implemented to enable the algorithm to adapt to the status of the search. This methodology ensures the comprehensive exploration of the entire solution space while simultaneously addressing the objectives of intensification and diversification. Additionally, in specific instances, the aspiration criterion is applied to supersede the Tabu list., is named as a pivot. Tabu tenure comes into play to navigate away from local optima throughout the search process. An iterative update of the list is implemented to enable the algorithm to adapt to the status of the search. This methodology ensures the comprehensive exploration of the entire solution space while simultaneously addressing the objectives of intensification and diversification. Additionally, in specific instances, the aspiration criterion is applied to supersede the Tabu list.Figure 4illustrates the proposed TS algorithm, where X* represents the best solution.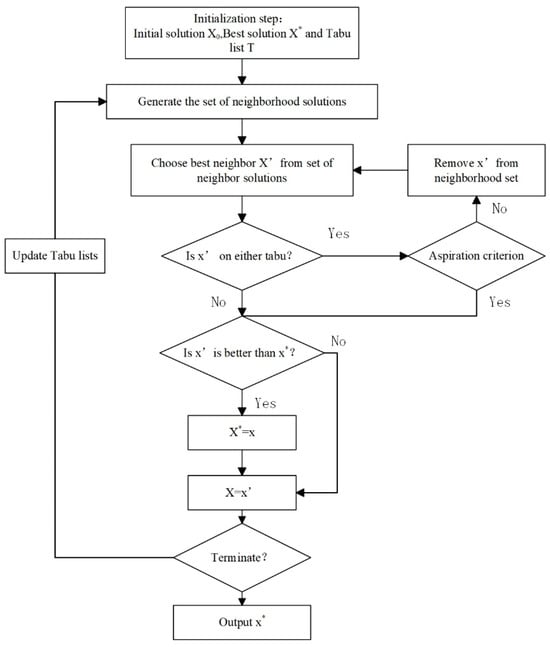 Figure 4.The flowchart of the Tabu search algorithm.The term of Tabu was determined from some preliminary experiments. The taboo retention period specified the upper limit for the number of iterations. The maximum computation time is set as the criterion for terminating the algorithm when no improvement is observed within the specified number of iterations. The second method uses integer programming with stochastic models, which are executed separately and then compared.
Figure 4.The flowchart of the Tabu search algorithm.The term of Tabu was determined from some preliminary experiments. The taboo retention period specified the upper limit for the number of iterations. The maximum computation time is set as the criterion for terminating the algorithm when no improvement is observed within the specified number of iterations. The second method uses integer programming with stochastic models, which are executed separately and then compared.4.4. Other Heuristic Algorithm
4.4.1. Problem Description
A heuristic optimization algorithm is an intuitively or empirically constructed algorithm that provides a viable solution for the combinatorial optimization problem at an acceptable cost, considering computational time and space constraints. This means that the heuristic algorithm solves the problem empirically or according to some rules, and the solution to the problem is not necessarily optimal but is likely to be approximate (or near optimal). Akbarzadeh et al. [124][80] proposed a three-phase heuristic algorithm for constructing high-quality feasible solutions using column generation, which is further improved by local branching. The surgical case replanning and scheduling problem with resource rescheduling is investigated in the presence of a chunk release time when the OR planners aim to achieve equilibrium between the capacity and demand for operating rooms. The following equation involves four components that reflect the benefits, resulting in weighted sums of various metrics.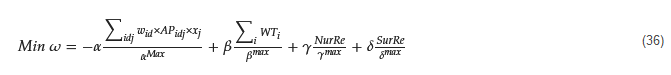 where the initial component compels the model to allocate surgical cases to an appropriate day. Following this, the second component seeks to minimize waiting time. Subsequently, the next component aims to minimize the overall nurse rescheduling cost. Finally, the last component focuses on minimizing the deviation of the surgeon’s schedule from the Master Surgery Schedule (MSS). The weights assigned to these different objective functions are relative and collectively sum to 1, i.e., α + β + γ + δ = 1.
where the initial component compels the model to allocate surgical cases to an appropriate day. Following this, the second component seeks to minimize waiting time. Subsequently, the next component aims to minimize the overall nurse rescheduling cost. Finally, the last component focuses on minimizing the deviation of the surgeon’s schedule from the Master Surgery Schedule (MSS). The weights assigned to these different objective functions are relative and collectively sum to 1, i.e., α + β + γ + δ = 1.4.4.2. Constraint
There needs to be a requirement for nurses to perform only one procedure at a time, and to assign procedures to nurses only if they have been assigned a shift. In fact, a surgeon is restricted to one operating room at any given time, and each surgery is limited to being conducted only once. In Equation (3719), 𝑁𝑇𝑛𝑡𝑑𝑗 denotes the case where nurse n received the task for schedule 𝑗 at time t on day 𝑑, 𝑥𝑗 indicates whether the scheduling is accepted or not, 𝑛𝑥𝑛𝑣𝑑 indicates whether nurse n worked on shift 𝑣 on day 𝑗; 𝑆𝑋𝑠𝑏𝑟𝑑𝑗 denotes whether surgeon s is assigned to the r-room b area on day d of program 𝑗; 𝐴𝑃𝑖𝑑𝑗 denotes if surgical case i is included in schedule 𝑗, day 𝑑; and 𝑃𝑋𝑖 is the decision variable implies that the surgery is performed within the time frame under consideration.
In Equation (3719), 𝑁𝑇𝑛𝑡𝑑𝑗 denotes the case where nurse n received the task for schedule 𝑗 at time t on day 𝑑, 𝑥𝑗 indicates whether the scheduling is accepted or not, 𝑛𝑥𝑛𝑣𝑑 indicates whether nurse n worked on shift 𝑣 on day 𝑗; 𝑆𝑋𝑠𝑏𝑟𝑑𝑗 denotes whether surgeon s is assigned to the r-room b area on day d of program 𝑗; 𝐴𝑃𝑖𝑑𝑗 denotes if surgical case i is included in schedule 𝑗, day 𝑑; and 𝑃𝑋𝑖 is the decision variable implies that the surgery is performed within the time frame under consideration.
4.4.3. Solution Methodology
The solution procedure named Column Generation and Local Branching Heuristic (CLH) is proposed to address the integrated problem. Figure 5 provides an overview for the solution procedure, consisting of three distinct steps. Firstly, the CLH algorithm employs a computationally feasible column generation procedure to address the impracticality of generating all possible OR schedules directly. If the solution is an integer, it is optimal; otherwise, transforming fractional solutions into feasible integer solutions offers an upper bound on the optimal solution. If the upper bound matches the lower, the optimal solution is identified. If not, the optimal upper bound is used as input for an improvement step, using local branches to narrow the optimality gap.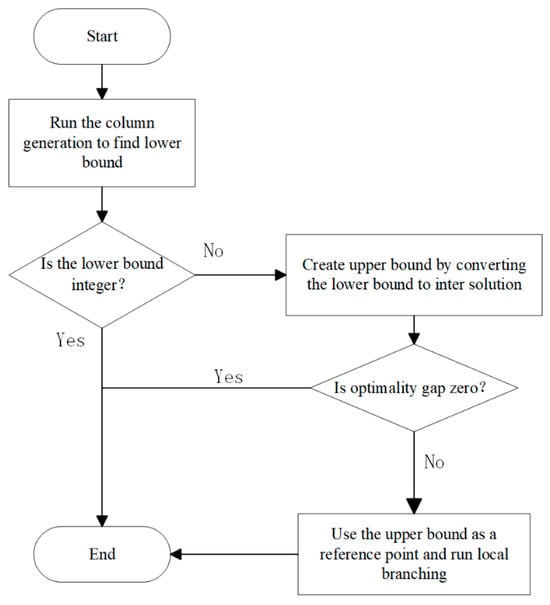 Figure 5.Summary of the Column Generation and Local Branching Heuristic.
Figure 5.Summary of the Column Generation and Local Branching Heuristic.
References
- Li, L. Development of China’s Health Care System in the Time of COVID-19: Challenges, Opportunities, and Call for Actions. Health Care Sci. 2022, 1, 33–40.
- Batko, K.; Ślęzak, A. The Use of Big Data Analytics in Healthcare. J. Big Data 2022, 9, 3.
- Gupta, D.; Denton, B. Appointment Scheduling in Health Care: Challenges and Opportunities. IIE Trans. 2008, 40, 800–819.
- Gao, K.; Shi, X.; Wang, W. The Life-Course Impact of Smoking on Hypertension, Myocardial Infarction and Respiratory Diseases. Sci. Rep. 2017, 7, 4330.
- Qu, L.; Gao, K.; Chen, X.; He, Q.; Ma, Y.; Peng, R. Optimal Quarantine Duration for Preventing Epidemic with Window Period. J. Infect. Non Infect. Dis. 2020, 5, 28.
- Alrefaei, M.H.; Diabat, A. Modelling and Optimization of Outpatient Appointment Scheduling. RAIRO-Oper. Res. 2015, 49, 435–450.
- Hulshof, P.J.H.; Vanberkel, P.T.; Boucherie, R.J.; Hans, E.W.; Van Houdenhoven, M.; Van Ommeren, J.-K.C.W. Analytical Models to Determine Room Requirements in Outpatient Clinics. OR Spectr. 2012, 34, 391–405.
- Huang, Y.-L.; Marcak, J. Grid Patient Appointment Template Design to Improve Scheduling Effectiveness. J. Healthc. Eng. 2015, 6, 239–258.
- Liu, N.; Finkelstein, S.R.; Kruk, M.E.; Rosenthal, D. When Waiting to See a Doctor Is Less Irritating: Understanding Patient Preferences and Choice Behavior in Appointment Scheduling. Manag. Sci. 2018, 64, 1975–1996.
- Wright, P.D.; Bretthauer, K.M.; Cote, M.J. Reexamining the Nurse Scheduling Problem: Staffing Ratios and Nursing Shortages. Decis. Sci. 2006, 37, 39–70.
- Talluri, K.; Van Ryzin, G. Revenue Management Under a General Discrete Choice Model of Consumer Behavior. Manag. Sci. 2004, 50, 15–33.
- Gao, K.; Wang, T.; Peng, K.; Wang, Z.; He, Q.; Peng, R. A Recursive Model of Residual Life Prediction for Human Beings with Health Information from Activities of Daily Living and Memory. Syst. Sci. Control Eng. 2021, 9, 529–541.
- Gao, K.; Peng, R.; Qu, L.; Xing, L.; Wang, S.; Wu, D. Linear System Design with Application in Wireless Sensor Networks. J. Ind. Inf. Integr. 2022, 27, 100279.
- Feldman, J.; Liu, N.; Topaloglu, H.; Ziya, S. Appointment Scheduling Under Patient Preference and No-Show Behavior. Oper. Res. 2014, 62, 794–811.
- Gupta, D.; Wang, W.-Y. Patient appointments in ambulatory care. In Handbook of Healthcare System Scheduling; Hall, R., Ed.; International Series in Operations Research & Management Science; Springer US: Boston, MA, USA, 2012; Volume 168, pp. 65–104. ISBN 978-1-4614-1733-0.
- Vieira, B.; Hans, E.W.; Van Vliet-Vroegindeweij, C.; Van De Kamer, J.; Van Harten, W. Operations Research for Resource Planning and -Use in Radiotherapy: A Literature Review. BMC Med. Inf. Decis. Mak. 2016, 16, 149.
- Leeftink, A.G.; Vliegen, I.M.H.; Hans, E.W. Stochastic Integer Programming for Multi-Disciplinary Outpatient Clinic Planning. Health Care Manag. Sci. 2019, 22, 53–67.
- Green, L.V.; Savin, S. Reducing Delays for Medical Appointments: A Queueing Approach. Oper. Res. 2008, 56, 1526–1538.
- Bobbie, A.; Karwowski, W. Simulation-Based Evaluation of Patient Appointment Policies for a Primary Care Clinic with Unscheduled Visits: A Case Study. Int. J. Hum. Factors Model. Simul. 2019, 7, 152.
- Lin, C.K.Y.; Ling, T.W.C.; Yeung, W.K. Resource Allocation and Outpatient Appointment Scheduling Using Simulation Optimization. J. Healthc. Eng. 2017, 2017, 9034737.
- Robinson, L.W.; Chen, R.R. Scheduling Doctors’ Appointments: Optimal and Empirically-Based Heuristic Policies. IIE Trans. 2003, 35, 295–307.
- Shonick, W. An Approach to Reducing the Adverse Effects of Broken Appointments in Primary Care Systems. Med. Care 1977, 15, 419–429.
- Chen, P.-S.; Hong, I.-H.; Hou, Y.; Shao, Y.-C. Healthcare Scheduling Policies in a Sequence-Number Based Appointment System for Outpatients’ Arrivals: Early, on Time, or Late? Comput. Ind. Eng. 2019, 130, 298–308.
- Tomkins, A.; Naylor, S.; Morgan, E. Short Message Service Cancellation Intervention to Reduce Integrated Sexual Health and HIV ‘Did Not Attend’ Appointment Rates. Int. J. STD AIDS 2019, 30, 201–203.
- Williamson, A.E.; Ellis, D.A.; Wilson, P.; McQueenie, R.; McConnachie, A. Understanding Repeated Non-Attendance in Health Services: A Pilot Analysis of Administrative Data and Full Study Protocol for a National Retrospective Cohort. BMJ Open 2017, 7, e014120.
- Dickey, W.; Morrow, J.I. Can Outpatient Non-Attendance Be Predicted from the Referral Letter? An Audit of Default at Neurology Clinics. J. R. Soc. Med. 1991, 84, 662–663.
- Barz, C.; Rajaram, K. Elective Patient Admission and Scheduling under Multiple Resource Constraints. Prod. Oper. Manag. 2015, 24, 1907–1930.
- Burke, E.K.; De Causmaecker, P.; Berghe, G.V.; Van Landeghem, H. The State of the Art of Nurse Rostering. J. Sched. 2004, 7, 441–499.
- Jansson, B. Choosing a Good Appointment System—A Study of Queues of the Type (D, M, 1). Oper. Res. 1966, 14, 292–312.
- Chiu, C.-K. Understanding Relationship Quality and Online Purchase Intention in E-Tourism: A Qualitative Application. Qual. Quant. 2009, 43, 669–675.
- Mak, H.-Y.; Rong, Y.; Zhang, J. Sequencing Appointments for Service Systems Using Inventory Approximations. Manuf. Serv. Oper. Manag. 2014, 16, 251–262.
- Denton, B.; Gupta, D. A Sequential Bounding Approach for Optimal Appointment Scheduling. IIE Trans. 2003, 35, 1003–1016.
- Klassen, K.J.; Rohleder, T.R. Outpatient Appointment Scheduling with Urgent Clients in a Dynamic, Multi-period Environment. Int. J. Serv. Ind. Manag. 2004, 15, 167–186.
- Cayirli, T.; Veral, E. Outpatient Scheduling in Health Care: A Review of Literature. Prod. Oper. Manag. 2009, 12, 519–549.
- Cayirli, T.; Veral, E.; Rosen, H. Designing Appointment Scheduling Systems for Ambulatory Care Services. Health Care Manag. Sci. 2006, 9, 47–58.
- Patrick, J.; Puterman, M.L.; Queyranne, M. Dynamic Multipriority Patient Scheduling for a Diagnostic Resource. Oper. Res. 2008, 56, 1507–1525.
- Solmaz, H. Comparison of Patients’ Admissions to the Cardiology Outpatient Clinics Between the Appointment System and the Queue System. Arch. Turk. Soc. Cardiol. 2023, 51, 188–195.
- Afrane, S.; Appah, A. Queuing Theory and the Management of Waiting-Time in Hospitals: The Case of Anglo Gold Ashanti Hospital in Ghana. Int. J. Acad. Res. Bus. Soc. Sci. 2014, 4, 34–44.
- Soriano, A.; Cayirli, T.; Yang, K.K.; Kong, Q.; Lee, C.-Y.; Teo, C.-P.; Zheng, Z.; Robinson, L.W.; Chen, R.R.; Denton, B.T.; et al. Comparison of Two Scheduling Systems. Oper. Res. 1966, 14, 388–397.
- LaGanga, L.R.; Lawrence, S.R. Appointment Overbooking in Health Care Clinics to Improve Patient Service and Clinic Performance. Prod. Oper. Manag. 2012, 21, 874–888.
- Shnits, B.; Bendavid, I.; Marmor, Y.N. An Appointment Scheduling Policy for Healthcare Systems with Parallel Servers and Pre-Determined Quality of Service. Omega 2020, 97, 102095.
- Cayirli, T.; Yang, K.K. Altering the Environment to Improve Appointment System Performance. Serv. Sci. 2019, 11, 138–154.
- Rohleder, T.; Klassen, K.J. Using Client-Variance Information to Improve Dynamic Appointment Scheduling Performance. Omega 2000, 28, 293–302.
- Creemers, S.; Lambrecht, M.R.; Beliën, J.; Van Den Broeke, M. Evaluation of Appointment Scheduling Rules: A Multi-Performance Measurement Approach. Omega 2021, 100, 102231.
- Bosch, P.M.V.; Dietz, D.C. Minimizing Expected Waiting in a Medical Appointment System. IIE Trans. 2000, 32, 841–848.
- Cayirli, T.; Yang, K.K.; Quek, S.A. A Universal Appointment Rule in the Presence of No-Shows and Walk-Ins. Prod. Oper. Manag. 2012, 21, 682–697.
- Klassen, K.J.; Yoogalingam, R. An Assessment of the Interruption Level of Doctors in Outpatient Appointment Scheduling. Oper. Manag. Res. 2008, 1, 95–102.
- Klassen, K.J.; Yoogalingam, R. Improving Performance in Outpatient Appointment Services with a Simulation Optimization Approach. Prod. Oper. Manag. 2009, 18, 447–458.
- Peng, Y.; Qu, X.; Shi, J. A Hybrid Simulation and Genetic Algorithm Approach to Determine the Optimal Scheduling Templates for Open Access Clinics Admitting Walk-in Patients. Comput. Ind. Eng. 2014, 72, 282–296.
- Meersman, T.; Maenhout, B. Multi-Objective Optimisation for Constructing Cyclic Appointment Schedules for Elective and Urgent Patients. Ann. Oper. Res. 2022, 312, 909–948.
- Ahmadi-Javid, A.; Jalali, Z.; Klassen, K.J. Outpatient Appointment Systems in Healthcare: A Review of Optimization Studies. Eur. J. Oper. Res. 2017, 258, 3–34.
- Robinson, L.W.; Chen, R.R. A Comparison of Traditional and Open-Access Policies for Appointment Scheduling. Manuf. Serv. Oper. Manag. 2010, 12, 330–346.
- Saghafian, S.; Austin, G.; Traub, S.J. Operations Research/Management Contributions to Emergency Department Patient Flow Optimization: Review and Research Prospects. IIE Trans. Healthc. Syst. Eng. 2015, 5, 101–123.
- Sauré, A.; Puterman, M.L. The Appointment Scheduling Game. INFORMS Trans. Educ. 2014, 14, 73–85.
- Wang, W.-Y.; Gupta, D. Adaptive Appointment Systems with Patient Preferences. Manuf. Serv. Oper. Manag. 2011, 13, 373–389.
- Kong, Q.; Lee, C.-Y.; Teo, C.-P.; Zheng, Z. Scheduling Arrivals to a Stochastic Service Delivery System Using Copositive Cones. Oper. Res. 2013, 61, 711–726.
- Erdogan, S.A.; Denton, B. Dynamic Appointment Scheduling of a Stochastic Server with Uncertain Demand. INFORMS J. Comput. 2013, 25, 116–132.
- Turkcan, A.; Zeng, B.; Muthuraman, K.; Lawley, M. Sequential Clinical Scheduling with Service Criteria. Eur. J. Oper. Res. 2011, 214, 780–795.
- Ozen, A.; Balasubramanian, H. The Impact of Case Mix on Timely Access to Appointments in a Primary Care Group Practice. Health Care Manag. Sci. 2013, 16, 101–118.
- Balasubramanian, H.; Biehl, S.; Dai, L.; Muriel, A. Dynamic Allocation of Same-Day Requests in Multi-Physician Primary Care Practices in the Presence of Prescheduled Appointments. Health Care Manag. Sci. 2014, 17, 31–48.
- Dharmadhikari, N.; Zhang, D.J. Simulation Optimization of Blocking Appointment Scheduling Policies for Multi-Clinic Appointments in Centralized Scheduling Systems. Ph.D. Thesis, North Dakota State University, Fargo, ND, USA, 2013. Volume 2.
- Cordier, J.-P.; Riane, F. Towards a Centralised Appointments System to Optimise the Length of Patient Stay. Decis. Support. Syst. 2013, 55, 629–639.
- Aslani, N.; Zhang, J. Integration of Simulation and DEA to Determine the Most Efficient Patient Appointment Scheduling Model for a Specific Healthcare Setting. J. Ind. Eng. Manag. 2014, 7, 785–815.
- Gao, K.; Peng, R.; Qu, L.; Wu, S. Jointly Optimizing Lot Sizing and Maintenance Policy for a Production System with Two Failure Modes. Reliab. Eng. Syst. Saf. 2020, 202, 106996.
- Bai, G.; Chi, Y.; Gao, K.; Peng, R. Reliability Evaluation of Multi-State Systems with Common Bus Performance Sharing Considering Performance Excess. IEEE Access 2022, 10, 19174–19185.
- Lei, B.; Ren, Y.; Luan, H.; Dong, R.; Wang, X.; Liao, J.; Fang, S.; Gao, K. A Review of Optimization for System Reliability of Microgrid. Mathematics 2023, 11, 822.
- Gao, K.; Wang, T.; Han, C.; Xie, J.; Ma, Y.; Peng, R. A Review of Optimization of Microgrid Operation. Energies 2021, 14, 2842.
- El-Sharo, M.; Zheng, B.; Yoon, S.W.; Khasawneh, M.T. An Overbooking Scheduling Model for Outpatient Appointments in a Multi-Provider Clinic. Oper. Res. Health Care 2015, 6, 1–10.
- Nguyen, T.B.T.; Sivakumar, A.I.; Graves, S.C. A Network Flow Approach for Tactical Resource Planning in Outpatient Clinics. Health Care Manag. Sci. 2015, 18, 124–136.
- Zeng, B.; Turkcan, A.; Lin, J.; Lawley, M. Clinic Scheduling Models with Overbooking for Patients with Heterogeneous No-Show Probabilities. Ann. Oper. Res. 2010, 178, 121–144.
- Savelsbergh, M.; Smilowitz, K. Stratified Patient Appointment Scheduling for Mobile Community-Based Chronic Disease Management Programs. IIE Trans. Healthc. Syst. Eng. 2016, 6, 65–78.
- Ren, Y.; Jin, C.; Fang, S.; Yang, L.; Wu, Z.; Wang, Z.; Peng, R.; Gao, K. A Comprehensive Review of Key Technologies for Enhancing the Reliability of Lithium-Ion Power Batteries. Energies 2023, 16, 6144.
- Homem-de-Mello, T.; Kong, Q.; Godoy-Barba, R. A Simulation Optimization Approach for the Appointment Scheduling Problem with Decision-Dependent Uncertainties. INFORMS J. Comput. 2022, 34, 2845–2865.
- Gao, K.; Yan, X.; Peng, R.; Xing, L. Economic Design of a Linear Consecutively Connected System Considering Cost and Signal Loss. IEEE Trans. Syst. Man. Cybern. Syst. 2021, 51, 5116–5128.
- Braune, R.; Gutjahr, W.J.; Vogl, P. Stochastic Radiotherapy Appointment Scheduling. Cent. Eur. J. Oper. Res. 2022, 30, 1239–1277.
- Fan, X.; Tang, J.; Yan, C.; Guo, H.; Cao, Z. Outpatient Appointment Scheduling Problem Considering Patient Selection Behavior: Data Modeling and Simulation Optimization. J. Comb. Optim. 2021, 42, 677–699.
- Dehghanimohammadabadi, M.; Rezaeiahari, M.; Seif, J. Multi-Objective Patient Appointment Scheduling Framework (MO-PASS): A Data-Table Input Simulation–Optimization Approach. Simulation 2023, 99, 363–383.
- Ala, A.; Alsaadi, F.E.; Ahmadi, M.; Mirjalili, S. Optimization of an Appointment Scheduling Problem for Healthcare Systems Based on the Quality of Fairness Service Using Whale Optimization Algorithm and NSGA-II. Sci. Rep. 2021, 11, 19816.
- Garaix, T.; Rostami, S.; Xie, X. Daily Outpatient Chemotherapy Appointment Scheduling with Random Deferrals. Flex. Serv. Manuf. J. 2020, 32, 129–153.
- Akbarzadeh, B.; Moslehi, G.; Reisi-Nafchi, M.; Maenhout, B. The Re-Planning and Scheduling of Surgical Cases in the Operating Room Department after Block Release Time with Resource Rescheduling. Eur. J. Oper. Res. 2019, 278, 596–614.
