2. Vehicle Routing Problem

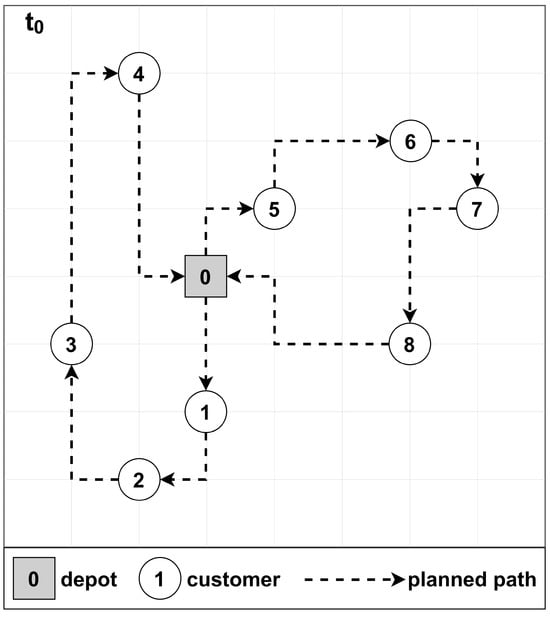
Figure 1.

Route planning of two vehicles.

2.1. Evolution and Quality of Information

-

Static and deterministic: All relevant data for the problem are available from the beginning and remain constant throughout the route execution. There are no unknown or uncertain elements, allowing for the design and execution of routes based on complete and fixed information. Figure 2 illustrates the planning and execution phases of a static and deterministic VRP. The planning phase (𝑡0) involves generating a feasible solution for the known problem inputs, such as customer requests. In the execution phase (𝑡𝑘−𝑛), the ongoing process of servicing customers unfolds. Although new inputs may arrive during this phase, the planned routes remain static. The process repeats at the termination phase (𝑡𝑘), where a new cycle begins with planning and execution based on new inputs.

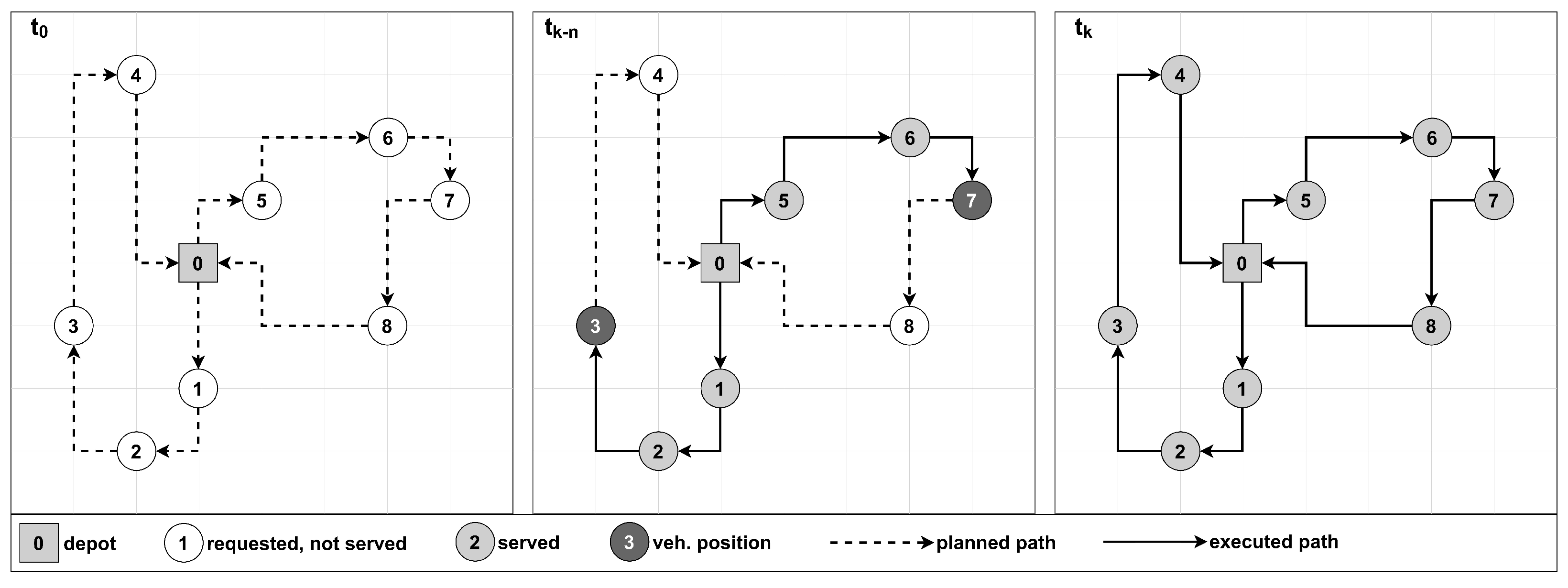Figure 2.

Example of static and deterministic vehicle routing.

-

Static and stochastic: Certain problem elements, such as requests, travel times, or demands, are only partially available and modelled with certain distribution functions. As the route executes, the actual values of these parameters become known. While routes are pre-designed, they can be adjusted as needed. For instance, the route has to be modified if a customer’s demand exceeds the forecasted demand and thus exceeds the available vehicle capacity. Figure 3 illustrates the static and stochastic VRP’s planning and execution phases. In the planning phase (𝑡0), a feasible solution is generated for known inputs like customer requests and associated demand values, which can be either deterministic or stochastic. For instance, request number three (3) features a stochastic demand. During the execution phase (𝑡𝑘−𝑛), as the vehicle services customers, unexpected issues may arise. At request number three (3), it is discovered that the initial estimate of the demand exceeds the vehicle’s capacity. Subsequently, a new feasible plan is devised, leading the vehicle to return to the depot, unload excess capacity, and then resume the route, including request number three (3). This cycle repeats in the termination phase (𝑡𝑘), initiating a new planning and execution cycle based on updated inputs.

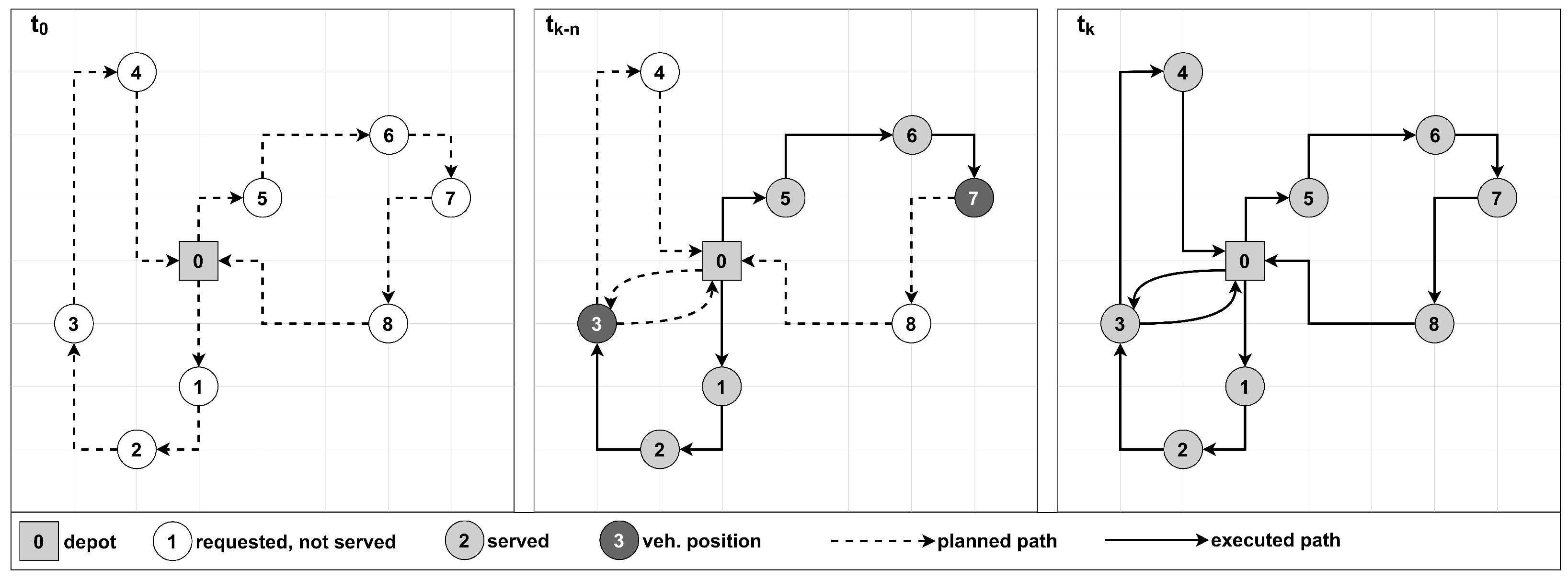Figure 3.

Example of static and stochastic vehicle routing.

-

Dynamic and deterministic: Some or all problem data are initially unavailable but gradually revealed during the planning and execution. There are no inherent uncertainties in the variables. For example, when a new dynamic event occurs, complete and fixed information about it becomes available at the time of the event. Figure 4 illustrates the planning and execution phases of a dynamic and deterministic VRP. The planning phase (𝑡0) involves generating a feasible solution to the known problem and the execution phase (𝑡𝑘−𝑛) allows for dynamic route adaptation to the changing conditions. New customer requests are revealed during execution and the DVRP accommodates their inclusion in the current routes, adhering to constraints. Dynamic adaptation aims to enhance fleet resource utilisation by promptly adjusting their plans to recent information.

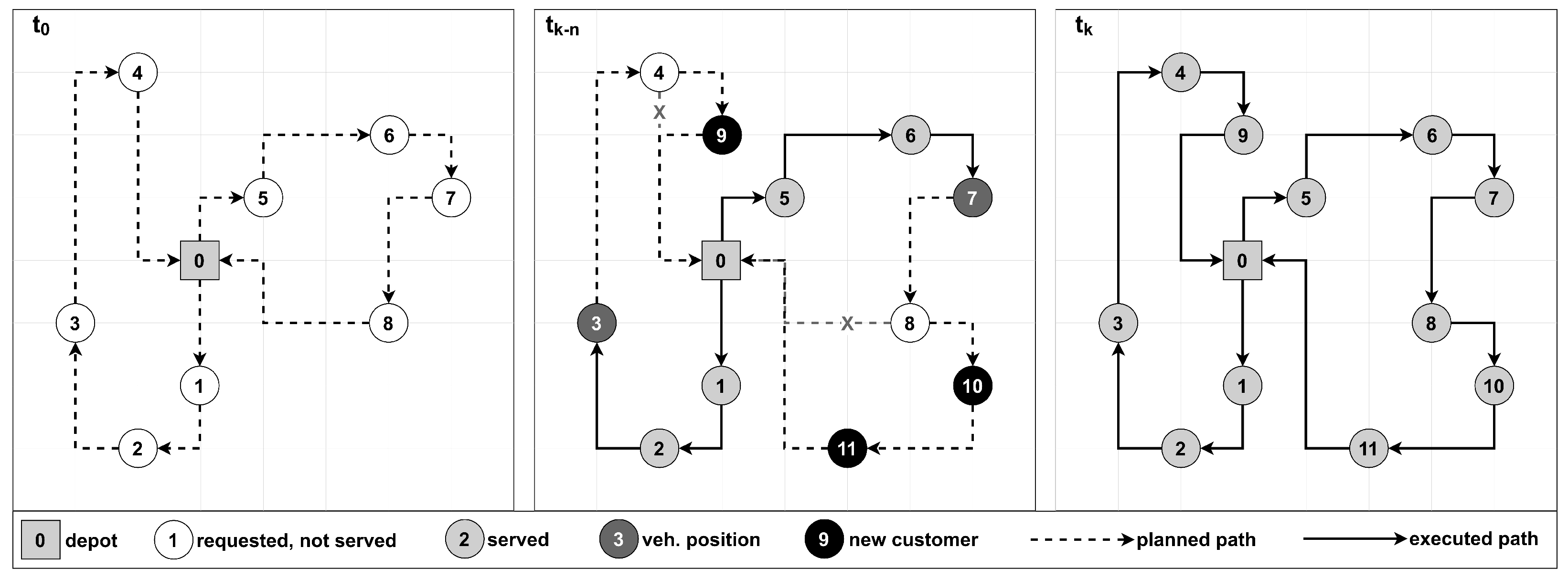Figure 4.

Example of dynamic and deterministic vehicle routing.

-

Dynamic and stochastic: This problem category involves gradual information revelation and stochastic variables that add uncertainty. Decision makers continuously sample probable (future) scenarios and adjust service sequences and routes in response to changing conditions and probability distributions. Figure 5 illustrates the planning and execution phases of a dynamic and stochastic VRP. In the left frame, the initial planning phase generated a set of feasible, optimised routes without accounting for probable future events. In the middle frame, the a priori planning phase considers known information and anticipated inputs sampled from probability distributions. Including such data in planning and execution horizons leads to proactive actions that enhance operational efficiency, customer satisfaction, and fleet resource utilisation.

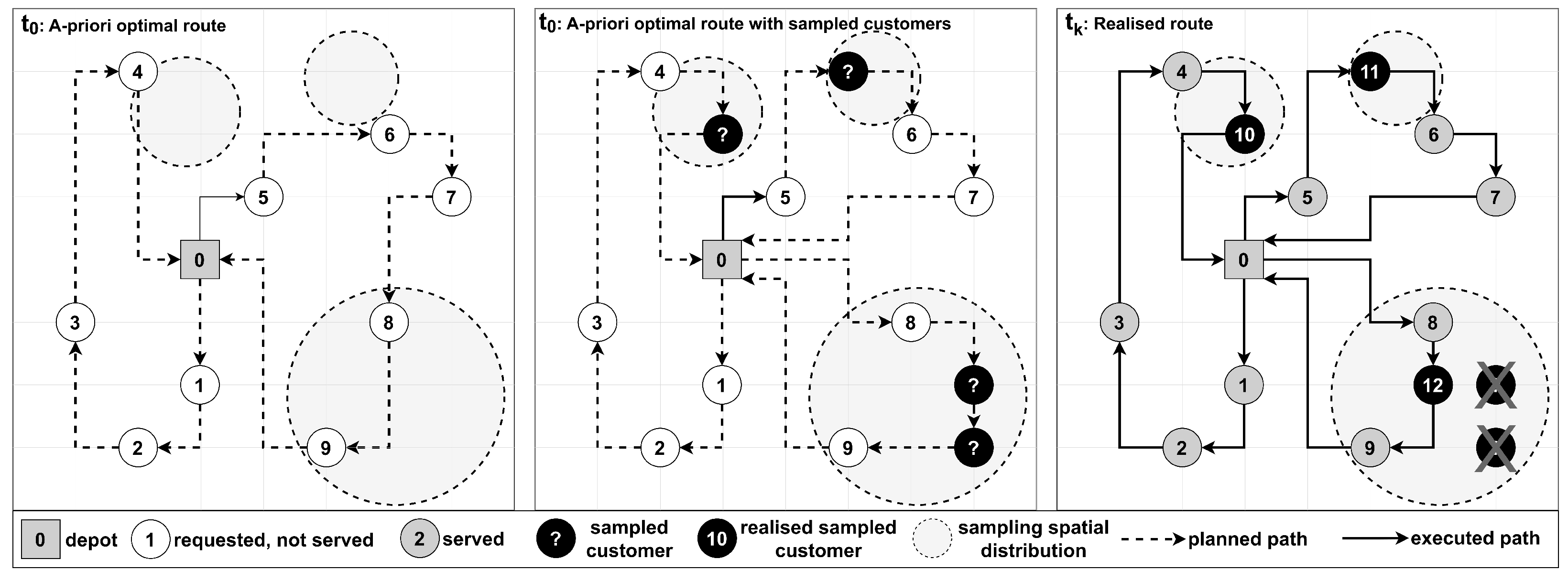Figure 5.

Example of dynamic vehicle routing with stochastic requests.

Understanding the characteristics of VRPs is crucial for effective route planning and optimisation. VRPs can be classified as static or dynamic based on whether the input data remains constant or changes over time. Deterministic VRPs assume all required input data is known during the route design phase. In contrast, stochastic VRPs involve stochasticity or variability in the input data, requiring probabilistic or random variables to represent specific components. Incorporating stochastic elements in VRPs enables anticipation and allows for robust, adaptive, and effective route planning and optimisation.

2.2. Conventional Solution Methods

Over the years, extensive research has been conducted on VRPs, since their formal definition in [12]^[4]. For a comprehensive overview of the VRP taxonomy, one may seek the review presented in [13]^[5]. Traditionally, the majority of VRPs were considered static and deterministic. Researchers have developed various solutions using Mixed Integer Programs (MIPs) based on mathematical graphs to generate optimal or near-optimal solutions for small instances. However, the non-polynomial complexity associated with VRPs, i.e., the solution space expands significantly as the problem size increases, making it computationally challenging to find optimal solutions for larger problem sizes using exact methods alone. To address this challenge, researchers have incorporated heuristics and metaheuristics in their solution approaches for VRPs. These enhanced approaches enable the application of VRPs to real-world scenarios, including large problem instances.

2.2.1. Exact Algorithms

Exact algorithms are highly effective for solving VRPs by finding the optimal solution. In the case of VRP instances with 50 to 100 customers, problem solvers can employ various exact methods, including branch and bound [14^[6][7],15], dynamic programming [16]^[8], linear integer programming [17]^[9], and more. These methods systematically explore the solution space to determine the optimal routing configuration that minimises the objective function.

2.2.2. Heuristic Algorithms

As optimisation algorithms, heuristics are employed to obtain satisfactory solutions within a reasonable timeframe. Heuristics leverage problem-specific knowledge and experience to guide the search for feasible solutions. They may involve trial and error, approximation, or problem simplification and do not guarantee finding the optimal solution. However, they can often find good solutions quickly and are widely used in practice due to their efficiency. There is a tradeoff between the runtime and solution quality of heuristics for the VRP. The quality of the final solution tends to improve the longer the heuristics are executed. Heuristics for the VRP can be divided into constructive and improvement heuristics [18]^[10]. Constructive heuristics for the VRP are algorithms that generate a solution by constructing routes through the set of customers. These heuristics use intuitive strategies, such as adding the nearest unvisited customer to the route until all customers are visited. Noteworthy constructive heuristics for the VRP include the Clarke and Wright savings algorithm [19]^[11], nearest and farthest insertion [20]^[12], and nearest neighbour [20]^[12] methods. These heuristics can be executed in serial or parallel mode, depending on the algorithm and available computational resources [21]^[13]. Selecting an appropriate solution construction approach is vital as it significantly impacts the search space, the likelihood of finding the optimal solution, and the overall running time. Improvement heuristics are algorithms that explore the neighbourhood of the current solution to improve the VRP solution [22]^[14]. Within the VRP domain, they are often referred to as Local Search (LS) procedures. These heuristics iteratively modify the current solution by applying minor changes and evaluating the resulting improvement in the objective function. Notable operators used in local search heuristics include relocate and exchange operators [23]^[15], or-opt-k operators [24]^[16], and 2-opt operators [25]^[17]. These heuristics effectively enhance the solution quality by focusing on the immediate neighbourhood of the current solution. However, it is vital to consider their sensitivity to the initial solution and the specific search neighbourhood employed, as they may converge to local optima. When combined with other heuristics or metaheuristics, local search operators can improve the quality of VRP solutions [18]^[10]. Using multiple local search improvements in a single algorithm iteration for a VRP route can improve the quality of the solution and make the overall algorithm faster [26]^[18]. This approach requires fewer moves as the operators work together to find a better solution, potentially reducing the number of iterations needed to converge to a high-quality solution. The key is ensuring that the applied operators do not interfere with each other. One way to achieve this is to use algorithms that operate on different parts of the solution space, such as exchanging pairs of customers in the route or reordering sub-sequences of the route. By acting on different segments of the solution space, the operators are less likely to interfere with each other and can work together to find a better solution more efficiently.

2.2.3. Metaheuristic Algorithms

Metaheuristics are a broad class of optimisation algorithms that enhance the probability of escaping the local optimums by exploring the usually vast solution search space [21]^[13]. Local optimums are defined as solutions that may be optimal only within a limited region of the solution space. In achieving the globally optimal solution, metaheuristics must explore the broader solution space and avoid getting trapped in the optima. This exploration process may involve accepting deteriorated objective function values and generating infeasible solutions, thereby diversifying the search space and increasing the likelihood of finding the global optimum ^[1]. Metaheuristics strike a balance between exploring the solution space and intensifying search efforts in specific regions, allowing them to search widely for new solutions while also improving solutions within targeted areas. Notable population-based metaheuristics for the VRP include the genetic algorithm [27]^[19], scatter search [28]^[20], ant colony optimisation [29]^[21], artificial bee colony [30]^[22], and particle swarm optimisation [31,32]^[23][24]. Furthermore, noteworthy neighbourhood-oriented metaheuristics for the VRP encompass simulated annealing [33^[25][26][27],34,35], taboo search [36^[28][29],37], variable neighbourhood search [38]^[30], iterated local search [39]^[31], and adaptive large neighbourhood search [40,41]^[32][33].

2.2.4. Hyper-Heuristic Algorithms

Hyper-heuristics are metaheuristics that provide adaptability to handle various problem instances by leveraging the observation that particular problem-solving approaches, i.e., heuristics, exhibit superior performance in specific cases. The domain encompasses two distinctive branches: selective and generative hyper-heuristics. Through the dynamic selection of algorithms based on measurable instance features, selective hyper-heuristics enable the identification of the most suitable heuristic for each problem instance. This flexibility enhances the overall solution quality and effectiveness in VRPs by harnessing the strengths of different heuristics. Addressing the Algorithm Selection Problem (ASP) in dynamic VRP problem instances, the authors in [42]^[34] utilised a simulation-based supervised learning approach. They evaluated 72,000 instances using 432,000 simulations, comparing the performance of the Greedy and Replanning algorithms. The aim was to differentiate problem instances based on measurable features, after which the suggested framework would select the most suitable algorithm for each. The problem instances were distinguished via classification, regression models, and Artificial Neural Networks (ANN). The authors concluded that out of the two examined algorithms, the Greedy algorithm outperformed Replanning in particular problem instances, highlighting the need to leverage algorithms based on specific problem characteristics. In another study, the authors provided a definition of algorithm building blocks and a measure of algorithm quality, where generative hyper-heuristics employ automated processes to evolve heuristics tailored to specific problem instances [43]^[35]. Unlike selective hyper-heuristics, which dynamically choose from pre-existing heuristics, generative heuristics explore algorithmic spaces, crafting novel heuristics optimised for unique routing challenges, demonstrating adaptability in dynamic and stochastic conditions [43]^[35]. Due to its flexible representation, one of the most prominent methods for automated heuristic generation methods is Genetic Programming (GP) [44]^[36]. One may find examples of approaches utilising GP in the domain of DVRPs and Electric Vehicle-DVRPs in the works presented in [43,44,45,46]^{[35][36][37][38]}.