Modeling and Control of Piezoelectric Actuators: Comparison
View Latest Version
Please note this is a comparison between Version 2 by Sirius Huang and Version 1 by Mithun Kanchan.

Piezoelectric actuators find extensive application in delivering precision motion in the micrometer to nanometer range. The advantages of a broader range of motion, rapid response, higher stiffness, and large actuation force from piezoelectric actuators make them suitable for precision positioning applications. However, the inherent nonlinearity in the piezoelectric actuators under dynamic working conditions severely affects the accuracy of the generated motion. The nonlinearity in the piezoelectric actuators arises from hysteresis, creep, and vibration, which affect the performance of the piezoelectric actuator. Thus, there is a need for appropriate modeling and control approaches for piezoelectric actuators, which can model the nonlinearity phenomenon and provide adequate compensation to achieve higher motion accuracy. 

  • capacitor insertion
  • digital charge control
  • Bouc–Wen model
  • Prandtl–Ishlinskii model
  • PID controller
  • sliding mode control
  • H∞ control

1. Introduction

The general requirement of precision motion in manufacturing and other commercial devices has led to extensive research and development in precision engineering. Having emerged as an integrated domain, precision engineering focuses on movement, measurement, and maintaining precision motion with higher accuracy and repeatability [1,2,3][1][2][3]. Piezoelectric actuators have been extensively used over the past few years as a source of precision positioning in a wide range of commercial applications. Piezoelectric actuators offer the advantage of precision motion in a few nanometers range to the tens of micrometer range. Furthermore, the faster response, low voltage actuation, high stiffness/load capacity/force generation smooth, backlash-free motion, non-magnetic actuation, wear resilience, cleanroom compatibility, vacuum, and cryogenic condition, low energy consumption adds to the advantages of the piezoelectric actuators [4,5,6][4][5][6]. Typical application domains of the piezoelectric actuators include precision manufacturing, fluidic applications, medical technology, micro-optics, aviation, defense, automation, robotics, aerospace, and consumer electronics.
Piezoelectric actuators are effectively employed in different applications such as micropumps/microreactors/micromixers [7[7][8],8], micromanipulators [9,10][9][10], microvalves [11], micro jet dispensers [12,13][12][13], atomic force microscopes [14[14][15],15], tool feed mechanisms [16[16][17],17], vibration isolation systems [18], etc. Piezoelectric actuators suffer from system nonlinearity when operated under dynamic conditions despite many advantages. The inherent hysteresis and creep limit the performance of the piezoelectric actuators under dynamic conditions, leading to nonlinearity in the system. Moreover, a badly damped system leads to undesirable vibrations, which add to the nonlinearity [4,19,20][4][19][20]. 

2. Overview of the Piezoelectric Actuation System

Piezoelectric actuators are a class of electromechanical devices that convert electrical signals to precise, controllable displacement. Typically, piezoelectric actuators are made of a group of smart materials that possess the property of piezoelectricity due to electromechanical coupling, which produces electric charge or mechanical strain based on the input stimulus [21]. When subjected to an external force, the piezoelectric materials produce electric charges corresponding to the direct piezoelectric effect. The application of piezoelectric materials as precision actuators adopts the inverse piezoelectric effect, which develops mechanical strain based on the applied electric potential, which in turn produces precision motion [21,22,23][21][22][23]. The early stage of discovering piezoelectric materials constituted quartz, Rochelle salt, and tourmaline, producing a comparable piezoelectric effect. However, the commercial need for large-range precision motion led to the discovery of synthetic piezoelectric materials such as Lead Zirconium Titanate (PZT) [24], Barium Titanate (BaTiO3) [25], PVDF [26], ZnO [27], etc. Figure 1 represents the basic configuration of the piezoelectric actuators used in different applications. The basic configuration of piezoelectric actuators is unimorph and bimorph, wherein the single-layer or two-layer piezo materials are bonded onto the metal substrate [28,29][28][29]. The unimorph and bimorph actuators are also available in a cantilever configuration, which is more flexible and produces a significant range of motion. However, the cantilever configuration lacks generated force [30,31][30][31]. The piezoelectric tube actuators can generate linear or lateral motion and are effectively adopted in many precision motion applications [32,33][32][33]. The multi-layered stacked configuration of the piezoelectric actuators can operate in linear or shear mode to produce linear or lateral precision motion. The range of motion developed by the stacked configuration is limited; however, the blocked force generated has an advantage over other types of actuators [5,21,34,35][5][21][34][35]. The amplified piezo actuators are developed with a flexural-compliant structural member to enhance the deflection of the stacked piezo actuators. Flexural-based amplification enhances the deflection range of the stacked actuators with moderate force [36,37][36][37]. Typically, the amplified piezo actuators in elliptical type, rhombus type, bridge type, symmetric five bar type, honeycomb type, Scott–Russell type, and lever type are extensively used in precision positioning applications [21,38,39,40,41][21][38][39][40][41].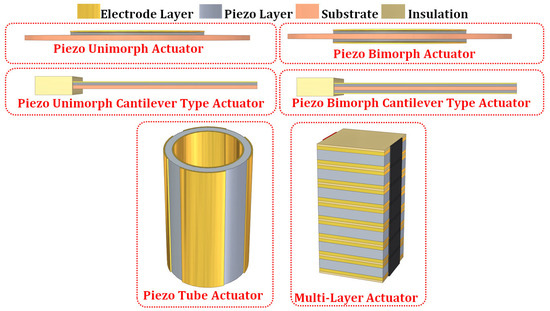
Technologies 11 00155 g002
Figure 1.
Basic configurations of the piezoelectric actuators.
Further advancement in piezoelectric actuator technology led to the development of stepping-piezoelectric actuators intended to generate a broader range of bi-directional linear and rotary motion. The stepping configuration of the piezoelectric actuators is also known as the piezo motor, which typically involves traditional piezoelectric actuators such as the unimorph/bimorph/multi-layered stacked actuators and the amplified piezo actuators as the primary source of actuation [21,42,43][21][42][43]. Inchworm piezoelectric motors [21[21][44][45],44,45], inertial piezoelectric motors [21[21][46][47],46,47], and ultrasonic piezoelectric motors [21,48,49][21][48][49] have been extensively reported in recent years which are effective in fulfilling the need of large range stepping motion. These piezoelectric motors can produce either linear/rotational motion or both, depending on the design and arrangement of the primary piezoelectric actuation mechanism. Researchers have also developed a series/parallel arrangement of multiple piezoelectric stepping stages to achieve multi-degree freedom linear/rotational motion along different coordinates [50,51][50][51]. A detailed review of different configurations of traditional, stepping, and multi-degree freedom piezoelectric actuators are presented in the works of Mohith et al. [21], Jianping Li et al. (2019) [52], Liang Wang et al. (2019) [53], and Shupeng Wang et al. (2019) [54]. The traditional piezoelectric actuators such as unimorph, bimorph, tube, and multi-layered actuators are a primary source of precision actuation in many commercial actuation systems. The constitutive Equations (1) and (2) represent the piezoelectric phenomena occurring in piezoelectric actuators is represented as follows [55] (IEEE Ultrasonics, Ferroelectrics, and Frequency Control Society)
ε i = e i j E σ j + d k i E k
D m = d m j σ j + ϵ m k T E k
where σ and ε correspond to the stress tensor and strain tensor, D and E correspond to the vector representing the electric displacement and the electric field, d represents the piezoelectric material constant, eE the elastic compliance matrix, ϵT represents the dielectric constant, i, j = 1, 2, 3, 4, 5, 6 and m, k = 1, 2, 3 refers to the different directions in the Cartesian coordinates. As observed in Equations (1) and (2), the mechanical strain developed in the piezoelectric materials follows a linear relationship with the applied electric field. However, when the piezoelectric actuators are put into operation under dynamic conditions, there exist system nonlinearities that affect the performance of the piezoelectric actuators. Therefore, there is a need for better modeling and control approaches that can model the inherent system nonlinearities of the piezoelectric actuation systems and minimize the error occurring due to nonlinearity through appropriate compensation models and control strategies.

3. Comprehensive Dynamic System Model and Modeling/Control Issues of the Piezoelectric Actuator

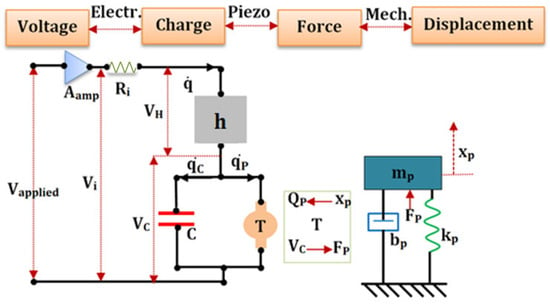
The promising potential of piezoelectric actuators has led to their application across wide ranges of precision manipulation to the extent of the nanometer scale. However, the dynamics of the piezoelectric actuator in specific applications lead to inherent nonlinearity that causes positioning errors. Thus, the development of modeling and control strategies for minimizing the nonlinearity errors in piezoelectric actuators have been given considerable attention. The constitutive relationship of piezoelectric materials (Equations (1) and (2)) does not account for any dynamic nonlinearity in the piezoelectric actuators. The nonlinearity emanates from hysteresis and creep, which significantly degrades the performance of the piezoelectric actuators in dynamic applications. Moreover, a badly damped system with piezoelectric actuation leads to dynamic vibrations, adding to the system’s nonlinearity [55,56][55][56]. Figure 2 represents the schematic of nonlinearity occurring in the piezoelectric actuators due to hysteresis, creep, and vibration. Hysteresis in the piezoelectric actuators occurs due to specific extrinsic contributions that induce nonlinearity between the actuation voltage and precision output displacement. The extent of hysteresis error depends on the present value of the input voltage and the previous history, thus developing a memory-based phenomenon. The amplitude and the frequency of the actuation signals majorly affect the extent of hysteresis error occurring under the dynamic operation of the piezoelectric actuators. Thus, the hysteresis in piezoelectric actuators shows either amplitude-dependent or rate-dependent behavior. The model approximating the hysteresis is either rate-dependent or rate-independent [56,57,58,59,60,61,62][56][57][58][59][60][61][62]. The piezoelectric actuators under dynamic operation experience hysteresis error of about 15%, but with the increase in the driving frequency of the actuation signal, the error can shoot up to almost 35%, thus leading to the error in precision motion [55].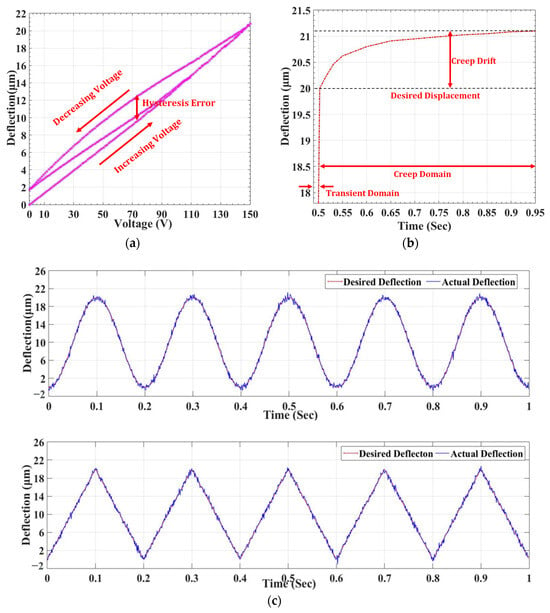
Technologies 11 00155 g003
Figure 2.
Schematic representation of the nonlinearity in the piezoelectric actuators due to (
a
) hysteresis, (
b
) creep, and (
c
) Vibration.
The creep in the piezoelectric actuators occurs due to the effect of applied electric potential on the remnant polarization of the electric dipole. The root cause for creep drift is the realignment of the crystal structure on the application of the electric field. The effect of creep drift significantly occurs at a low speed of operation and leads to a broad range of nonlinearity with the increase in time [55,56][55][56]. The combined effect of hysteresis and creep hinders the performance of the piezoelectric actuators in precision positioning applications where higher accuracy and precision are the significant criteria [57,58,59,60,61,62][57][58][59][60][61][62]. Implementing an appropriate modeling approach can model the piezoelectric actuator system behavior under hysteresis and creep, which can provide suitable compensation by adopting proper control approaches to overcome the nonlinearity errors. The piezoelectric actuators are modeled as a combination of electrical and mechanical systems based on the electromechanical interaction at different stages [63,64,65][63][64][65]. Figure 3 represents the schematic of the electromechanical model of the piezoelectric actuator. Goldfarb et al. [63] developed and implemented the following electromechanical model of the piezoelectric actuator with hysteresis nonlinearity. Adriaens et al. [64] also adopted a similar approach in defining the electromechanical model of the piezoelectric actuator with hysteresis. Gao et al. [63] proposed a linear modeling approach with the electromechanical interaction, which excluded the effect of nonlinearity occurring due to hysteresis.
Technologies 11 00155 g004
Figure 3.
Schematic representation of the electromechanical model of the piezoelectric actuator.
Mathematically the comprehensive dynamic model of the piezoelectric actuator can be written as shown in Equations (3)–(9)
A a m p V i t = V h t + V C t + R i q t
V H t = h q
q t = q c t + q P t
V C t = q C t / C
q P t = T x P t
F P = T V C t
m p x ¨ p t + b p x ˙ p t + k p x p t = F P
where Vapplied is the control voltage fed through a linear amplifier of gain Aamp, Ri is the overall resistance of the driving circuit. Vi is the amplified voltage that drives the piezo actuator, q and q˙ are the total charge and current through the circuit, H and T represent the hysteresis and electromechanical piezo coefficient with corresponding voltage drop VH, VT, and C corresponds to the total capacitance of the piezoelectric circuit which stores charge qc. The piezoelectric effect induces a charge of qP across the transformer element T. The conversion of the applied voltage across the piezoelectric element induces force FP with the piezoelectric element of mass mP, stiffness kP, and damping coefficient of bP, resulting in the displacement of xP.

References

  1. Jia, Z.-Y.; Ma, J.-W.; Song, D.-N.; Wang, F.-J.; Liu, W. A review of contouring-error reduction method in multi-axis CNC machining. Int. J. Mach. Tools Manuf. 2018, 125, 34–54.
  2. Wang, H.; Li, Y.; Wang, X.; Liu, Z.; Ahmed, M.F.; Zeng, C. Preparation and characterization of piezoelectric foams based on cyclic olefin copolymer. Eng. Sci. 2021, 16, 203–210.
  3. Su, Y.-F.; Han, G.; Kong, Z.; Nantung, T.; Lu, N. Embeddable piezoelectric sensors for strength gain monitoring of cementitious materials: The influence of Coating Materials. Eng. Sci. 2020, 11, 66–75.
  4. Muralidhara; Rao, R. Displacement characteristics of a piezo actuator-based prototype microactuator with a hydraulic displacement amplification system. J. Mech. Sci. Technol. 2015, 29, 4817–4822.
  5. Mohith, S.; Navin Karanth, P.; Kulkarni, S.M. Performance analysis of valveless micropump with disposable chamber actuated through Amplified Piezo Actuator (APA) for biomedical application. Mechatronics 2020, 67, 102347.
  6. Ling, M.; Cao, J.; Zeng, M.; Lin, J.; Inman, D.J. Enhanced mathematical modeling of the displacement amplification ratio for piezoelectric compliant mechanisms. Smart Mater. Struct. 2016, 25, 075022.
  7. Naik, N.; Suresh, P.; Yadav, S.; Nisha, M.P.; Arias-Gonzáles, J.L.; Cotrina-Aliaga, J.C.; Bhat, R.; Jalageri, M.D.; Kaushik, Y.; Kunjibettu, A.B. A review on composite materials for energy harvesting in electric vehicles. Energies 2023, 16, 3348.
  8. Mohith, S.; Karanth, P.N.; Kulkarni, S.M. Experimental investigation on performance of disposable micropump with retrofit piezo stack actuator for biomedical application. Microsyst. Technol. 2019, 25, 4741–4752.
  9. El-Sayed, A.M.; Abo-Ismail, A.; El-Melegy, M.T.; Hamzaid, N.A.; Osman, N.A.A. Development of a Micro-Gripper Using Piezoelectric Bimorphs. Sensors 2013, 13, 5826–5840.
  10. Abondance, T.; Jayaram, K.; Jafferis, N.T.; Shum, J.; Wood, R.J. Piezoelectric Grippers for Mobile Micromanipulation. IEEE Robot. Autom. Lett. 2020, 5, 4407–4414.
  11. Jeon, J.; Han, C.; Han, Y.-M.; Choi, S.-B. A new type of a direct-drive valve system driven by a piezostack actuator and sliding spool. Smart Mater. Struct. 2014, 23, 075002.
  12. Sohn, J.W.; Choi, S.-B. Identification of Operating Parameters Most Strongly Influencing the Jetting Performance in a Piezoelectric Actuator-Driven Dispenser. Appl. Sci. 2018, 8, 243.
  13. Deng, G.; Cui, W.; Zhou, C.; Li, J. A piezoelectric jetting dispenser with a pin joint. Optik 2018, 175, 163–171.
  14. Cai, K.; Tian, Y.; Wang, F.; Zhang, D.; Shirinzadeh, B. Development of a piezo-driven 3-DOF stage with T-shape flexible hinge mechanism. Robot. Comput. Manuf. 2016, 37, 125–138.
  15. Eslami, B.; Solares, S.D. Experimental approach for selecting the excitation frequency for maximum compositional contrast in viscous environments for piezo-driven bimodal atomic force microscopy. J. Appl. Phys. 2016, 119, 084901.
  16. Muralidhara; Vasa, N.J.; Makaram, S. Investigations on a directly coupled piezoactuated tool feed system for micro-electro-discharge machine. Int. J. Mach. Tools Manuf. 2009, 49, 1197–1203.
  17. Tian, X.; Zhang, B.; Liu, Y.; Chen, S.; Yu, H. A novel U-shaped stepping linear piezoelectric actuator with two driving feet and low motion coupling: Design, modeling and experiments. Mech. Syst. Signal Process. 2019, 124, 679–695.
  18. Lu, Z.-Q.; Shao, D.; Fang, Z.-W.; Ding, H.; Chen, L.-Q. Integrated vibration isolation and energy harvesting via a bistable piezo-composite plate. J. Vib. Control 2020, 26, 779–789.
  19. Rodriguez-Fortun, J.M.; Orus, J.; Alfonso, J.; Gimeno, F.B.; Castellanos, J.A. Flatness-Based Active Vibration Control for Piezoelectric Actuators. IEEE/ASME Trans. Mechatron. 2013, 18, 221–229.
  20. Tavakolpour, A.R.; Mailah, M.; Mat Darus, I.Z.; Tokhi, O. Self-learning active vibration control of a flexible plate structure with piezoelectric actuator. Simul. Model. Pract. Theory 2010, 18, 516–532.
  21. Mohith, S.; Upadhya, A.R.; Navin, K.P.; Kulkarni, S.M.; Rao, M. Recent trends in piezoelectric actuators for precision motion and their applications: A review. Smart Mater. Struct. 2021, 30, 013002.
  22. Boukari, A.-F.; Carmona, J.-C.; Moraru, G.; Malburet, F.; Chaaba, A.; Douimi, M. Piezo-actuators modeling for smart applications. Mechatronics 2011, 21, 339–349.
  23. Xue, D.; Zhou, Y.; Bao, H.; Gao, J.; Zhou, C.; Ren, X. Large piezoelectric effect in Pb-free Ba(Ti, Sn)O3-x(Ba, Ca)TiO3 ceramics. Appl. Phys. Lett. 2011, 99, 122901.
  24. Su, X.; Jia, Y.; Han, C.; Hu, Y.; Fu, Z.; Liu, K.; Yu, Y.; Yan, X.; Wang, Y. Flash sintering of lead zirconate titanate ceramics under an alternating current electrical field. Ceram. Int. 2019, 45, 5168–5173.
  25. Kholodkova, A.A.; Danchevskaya, M.N.; Ivakin, Y.D.; Muravieva, G.P.; Smirnov, A.D.; Tarasovskii, V.P.; Ponomarev, S.G.; Fionov, A.S.; Kolesov, V.V. Properties of barium titanate ceramics based on powder synthesized in supercritical water. Ceram. Int. 2018, 44, 13129–13138.
  26. Naik, R.; Mohit, S.; Chavan, S. Piezoelectric property investigation on PVDF/ZrO2/ZnO nanocomposite for energy harvesting application. Eng. Res. Express 2021, 3, 025003.
  27. Colorado, S.A.; Colorado, H.A. Manufacturing of zinc oxide structures by thermal oxidation processes as scalable methods towards inexpensive electric generators. Ceram. Int. 2017, 43, 15846–15855.
  28. Bakhtiari-Shahri, M.; Moeenfard, H. Energy harvesting from unimorph piezoelectric circular plates under random acoustic and base acceleration excitations. Mech. Syst. Signal Process. 2019, 130, 502–523.
  29. Rios, S.A.; Fleming, A.J. A new electrical configuration for improving the range of piezoelectric bimorph benders. Sens. Actuators A Phys. 2015, 224, 106–110.
  30. Ozaki, T.; Hamaguchi, K. Performance of direct-driven flapping-wing actuator with piezoelectric single-crystal PIN-PMN-PT. J. Micromech. Microeng. 2018, 28, 025007.
  31. Almeida, A.; Andrews, G.; Jaiswal, D.; Hoshino, K. The Actuation Mechanism of 3D Printed Flexure-Based Robotic Microtweezers. Micromachines 2019, 10, 470.
  32. Habineza, D.; Rakotondrabe, M.; Le Gorrec, Y. Bouc–Wen Modeling and Feedforward Control of Multivariable Hysteresis in Piezoelectric Systems: Application to a 3-DoF Piezotube Scanner. IEEE Trans. Control Syst. Technol. 2015, 23, 1797–1806.
  33. Habineza, D.; Rakotondrabe, M.; Le Gorrec, Y. Simultaneous suppression of badly damped vibrations and cross-couplings in a 2-DoF piezoelectric actuator by using feedforward standard H∞ approach. In Next-Generation Robotics II; and Machine Intelligence and Bio-Inspired Computation: Theory and Applications IX; SPIE: Baltimore, MD, USA, 2015; p. 94940L.
  34. Bu, Z.; Lin, S.; Huang, X.; Li, A.; Wu, D.; Zhao, Y.; Luo, Z.; Wang, L. A novel piezostack-driven jetting dispenser with corner-filleted flexure hinge and high-frequency performance. J. Micromech. Microeng. 2018, 28, 075001.
  35. Hwang, H.S.; Nasser, J.; Sodano, H.A. Piezoelectric Stack Actuator for Measurement of Interfacial Shear Strength at High Strain Rates. Exp. Mech. 2019, 59, 979–990.
  36. Santhya, M.; Upadhya, A.R.; Panambur, N.K.; Kulkarni, S.M. Performance analysis of a novel piezo actuated valveless micropump for biomedical application. AIP Conf. Proc. 2020, 2236, 070002.
  37. Dsouza, R.D.; Navin, K.P.; Theodoridis, T.; Sharma, P. Design, fabrication and testing of a 2 DOF compliant flexural microgripper. Microsyst. Technol. 2018, 24, 3867–3883.
  38. Dong, W.; Chen, F.; Yang, M.; Du, Z.-J.; Tang, J.; Zhang, D. Development of a highly efficient bridge-type mechanism based on negative stiffness. Smart Mater. Struct. 2017, 26, 095053.
  39. Chen, F.; Du, Z.-J.; Yang, M.; Gao, F.; Dong, W.; Zhang, D. Design and analysis of a three-dimensional bridge-type mechanism based on the stiffness distribution. Precis. Eng. 2018, 51, 48–58.
  40. Dong, W.; Chen, F.; Gao, F.; Yang, M.; Sun, L.; Du, Z.; Tang, J.; Zhang, D. Development and analysis of a bridge-lever-type displacement amplifier based on hybrid flexure hinges. Precis. Eng. 2018, 54, 171–181.
  41. Chen, F.; Gao, Y.; Dong, W.; Du, Z. Design and Control of a Passive Compliant Piezo-Actuated Micro-Gripper With Hybrid Flexure Hinges. IEEE Trans. Ind. Electron. 2020, 68, 11168–11177.
  42. Tian, X.; Liu, Y.; Chen, W.; Deng, J.; Liu, J. Development and experiment evaluation of an H-shape linear piezoelectric actuator operated in stepping mode. Ceram. Int. 2018, 44, S246–S249.
  43. Wang, Y.-J.; Yang, C.; Sue, C.-Y.; Wang, Y.-T. Analysis of a 0.1-μm stepping bi-axis piezoelectric stage using a 2-DOF lumped model. Microsyst. Technol. 2020, 26, 425–436.
  44. Li, J.; Zhao, H.; Shao, M.; Zhou, X.; Huang, H.; Fan, Z. Design and experiment performances of an inchworm type rotary actuator. Rev. Sci. Instrum. 2014, 85, 085004.
  45. Shao, S.; Song, S.; Liu, K.; Xu, M. A piezo-driven rotary inchworm actuator featured with simple structure and high output torque. Int. J. Appl. Electromagn. Mech. 2019, 59, 317–325.
  46. Zhong, B.; Zhu, J.; Jin, Z.; He, H.; Sun, L.; Wang, Z. Improved inertial stick-slip movement performance via driving waveform optimization. Precis. Eng. 2019, 55, 260–267.
  47. Gao, Q.; He, M.; Lu, X.; Zhang, C.; Cheng, T. Simple and high-performance stick-slip piezoelectric actuator based on an asymmetrical flexure hinge driving mechanism. J. Intell. Mater. Syst. Struct. 2019, 30, 2125–2134.
  48. Grybas, I.; Bansevicius, R.; Jurenas, V.; Bubulis, A.; Janutenaite, J.; Kulvietis, G. Ultrasonic standing waves-driven high resolution rotary table. Precis. Eng. 2016, 45, 396–402.
  49. Wang, L.; Shu, C.; Zhang, Q.; Jin, J. A novel sandwich-type traveling wave piezoelectric tracked mobile system. Ultrasonics 2017, 75, 28–35.
  50. Liao, C.; Xu, M.; Xiao, R.; Han, W. Integrated design of piezo-actuated 2-DOF submillimeter-range super-resolution platform with self-sensing unit. Mech. Syst. Signal Process. 2020, 139, 106569.
  51. Chen, F.; Dong, W.; Yang, M.; Sun, L.; Du, Z. A PZT Actuated 6-DOF Positioning System for Space Optics Alignment. IEEE/ASME Trans. Mechatron. 2019, 24, 2827–2838.
  52. Li, J.; Huang, H.; Morita, T. Stepping piezoelectric actuators with large working stroke for nano-positioning systems: A review. Sens. Actuators A Phys. 2019, 292, 39–51.
  53. Wang, L.; Chen, W.; Liu, J.; Deng, J.; Liu, Y. A review of recent studies on non-resonant piezoelectric actuators. Mech. Syst. Signal Process. 2019, 133, 106254.
  54. Wang, S.; Rong, W.; Wang, L.; Xie, H.; Sun, L.; Mills, J.K. A survey of piezoelectric actuators with long working stroke in recent years: Classifications, principles, connections and distinctions. Mech. Syst. Signal Process. 2019, 123, 591–605.
  55. Gu, G.-Y.; Zhu, L.-M.; Su, C.-Y.; Ding, H.; Fatikow, S. Modeling and control of piezo-actuated nanopositioning stages: A survey. IEEE Trans. Autom. Sci. Eng. 2016, 13, 313–332.
  56. Rakotondrabe, M. Multivariable classical Prandtl–Ishlinskii hysteresis modeling and compensation and sensorless control of a nonlinear 2-dof piezoactuator. Nonlinear Dyn. 2017, 89, 481–499.
  57. Sabarianand, D.V.; Karthikeyan, P.; Muthuramalingam, T. A review on control strategies for compensation of hysteresis and creep on piezoelectric actuators based micro systems. Mech. Syst. Signal Process. 2020, 140, 106634.
  58. Gan, J.; Zhang, X. A review of nonlinear hysteresis modeling and control of piezoelectric actuators. AIP Adv. 2019, 9, 040702.
  59. Chen, J.; Peng, G.; Hu, H.; Ning, J. Dynamic Hysteresis Model and Control Methodology for Force Output Using Piezoelectric Actuator Driving. IEEE Access 2020, 8, 205136–205147.
  60. Chi, Z.; Xu, Q. Recent Advances in the Control of Piezoelectric Actuators. Int. J. Adv. Robot. Syst. 2014, 11, 182.
  61. Yang, Y. Piezoelectric Actuators Application and Hysteresis Modelling: A Brief Survey. Open Access Libr. J. 2023, 10, e10482.
  62. Hassani, V.; Tjahjowidodo, T.; Do, T.N. A survey on hysteresis modeling, identification and control. Mech. Syst. Signal Process. 2014, 49, 209–233.
  63. Goldfarb, M.; Celanovic, N. Modeling piezoelectric stack actuators for control of micromanipulation. IEEE Control Syst. 1997, 17, 69–79.
  64. Adriaens, H.J.M.T.S.; De Koning, W.L.; Banning, R. Modeling piezoelectric actuators. IEEE/ASME Trans. Mechatron. 2000, 5, 331–341.
  65. Gao, Y.; Zhang, D.; Yu, C.W. Dynamic modeling of a novel workpiece table for active surface grinding control. Int. J. Mach. Tools Manuf. 2001, 41, 609–624.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/)
ScholarVision Creations
Feedback