Reinforcement Learning, Knowledge Distillation, and Channel Pruning: Comparison
View Latest Version
Please note this is a comparison between Version 2 by Peter Tang and Version 1 by Ming Zhao.

The methods used for model compression and acceleration are primarily divided into five categories—network pruning, parameter quantization, low-rank decomposition, lightweight network design, and knowledge distillation—such that the scope of actions and design ideas for each method are different.

  • model compression
  • reinforcement learning
  • knowledge distillation

1. Introduction

Since the beginning of the 21st century, significant advancements have been achieved in deep neural networks regarding computer vision, particularly in image classification and object detection tasks [1,2,3,4,5,6][1][2][3][4][5][6]. Models based on deep neural networks have for several years been deemed superior to related models, owing to improvements in computer hardware that facilitate the design of more complex models that are trainable on larger datasets for extended periods and, consequently, facilitate the design of more optimized model effects. However, in numerous practical applications, the computing resources provided by hardware devices do not meet the requirements of complex models, making model compression an important research topic.
Currently, the methods used for model compression and acceleration are primarily divided into five categories—network pruning, parameter quantization, low-rank decomposition, lightweight network design, and knowledge distillation—such that the scope of actions and design ideas for each method are different. These methods are discussed herein with respect to the concept underlying their design, their function, the changes required in the network structure, and their advantages and disadvantages.
The most common method for model compression and acceleration is network pruning. To determine the importance of parameters in pruning, parameter evaluation criteria are devised and unimportant parameters are removed. The action position affects the convolution and fully connected layers in the network, necessitating changes to the original network structure. Representative studies of this method include structured and unstructured pruning (group- and filter-level pruning) [7,8,9,10][7][8][9][10]. An advantage of unstructured pruning is that a network can be compressed to any degree. However, most frameworks and hardware cannot accelerate sparse matrix calculations, thus complicating effective acceleration. Structured pruning can narrow the network and accelerate hardware, which can significantly affect accuracy.
In addition to network pruning, parameter quantization and knowledge distillation can operate on convolutional and fully connected layers without changing the network structure. The concept underlying the parameter quantization design involves replacing high-precision parameters with low-precision parameters to reduce the size of the network model. Knowledge distillation uses a large network with high complexity as the teacher model and a small network with low complexity as the student model. The teacher model guides the training of the student model with low complexity so that the performance of the small model is close to that of the large model. Representative studies on parameter quantization include binarization, ternary and cluster quantization, and mixed-bit-width quantization [11,12,13,14,15][11][12][13][14][15]. These parameters can significantly reduce the storage space and required memory, speed up the computation, and reduce the energy consumption of the equipment. However, training and fine-tuning are time consuming and the quantization of the special bit width can easily cause incompatibility with the hardware platform, along with poor flexibility.
In knowledge confrontation [16[16][17][18][19],17,18,19], distillations of the representative research output layer, mutual information, attention, and relevance, large networks can be compressed into a number of smaller networks. Resource-constrained devices, such as mobile platforms, can be deployed and easily combined with other compression methods to achieve a greater degree of compression, all of which are considered advantages. However, the network must be trained at least twice, which increases the training time and can be disadvantageous.
Low-rank decomposition and lightweight network design compress the model at the convolution layer and overall network levels, respectively. In low-rank decomposition, the original tensor is decomposed into a number of low-rank tensors; this has led to research achievements such as dual and multivariate decomposition [20,21[20][21][22][23],22,23], demonstrating good compression along with an acceleration effect on large convolution kernels and small- and medium-sized networks. This reflects comparatively mature research, as simplifying convolution and decomposing it into smaller kernels is difficult. However, layer-by-layer decomposition is not conducive to global parameter compression. Therefore, the lightweight network was designed to be suitable for deployment in mobile devices using a compact and efficient network structure. Representative research achievements include SqueezeNet, Shuffle Net, Mobile Net, Split Net and Morph Net [24,25,26,27,28,29][24][25][26][27][28][29]. These advantages include simple network training, a short training time, small networks with a small storage capacity, low computation, and good network performance, which are suitable for deployment in resource-constrained devices such as mobile platforms. However, combining a special structure with other compression and acceleration methods is difficult, which leads to poor generalization, making it unsuitable as a pre-training model for other models.
In these compression methods, the model size and accuracy must be considered. Therefore, experts in this field conduct multiple experiments, set different model compression ratios, and observe the test results to determine a model that satisfies the requirements using a time-consuming procedure. Hence, some scholars have proposed automatic pruning technologies. He et al. [30] proposed an automatic pruning model based on reinforcement learning, where a pretrained network model was processed layer by layer. The input of the algorithm is the representation vector of each layer, a useful feature of the layer. The output of the algorithm is the compression ratio. When a layer is compressed at this ratio, the algorithm proceeds to the next layer. When all layers are compressed, the model is tested on the validation set without fine-tuning because the accuracy of the validation set has been established. When the search is complete, the optimal model (with the highest reward value) is selected and fine-tuned to obtain the final model effect.

2. Reinforcement Learning

Reinforcement learning is an important branch of machine learning that aims to study and develop how agents learn and formulate optimal behavioral strategies in their interactions with the environment in order to maximize accumulated rewards or goals. This field is characterized by agent learning through trial and error and feedback, without the need for pre-labeled data or explicit rules. Reinforcement learning mainly comprises the agent, environment, state, action, and rewards. After the agent performs an action, the environment transitions to a new state where a reward signal (positive or negative) is given to the environment. Subsequently, the agent performs new actions according to a certain strategy based on the new state and feedback received from the environmental reward. In this process, the agent and environment interact through states, actions, and rewards. Through reinforcement learning, the agent can determine its state and the actions it should take to obtain the maximum reward. Figure 1 shows the general flowchart of reinforcement learning.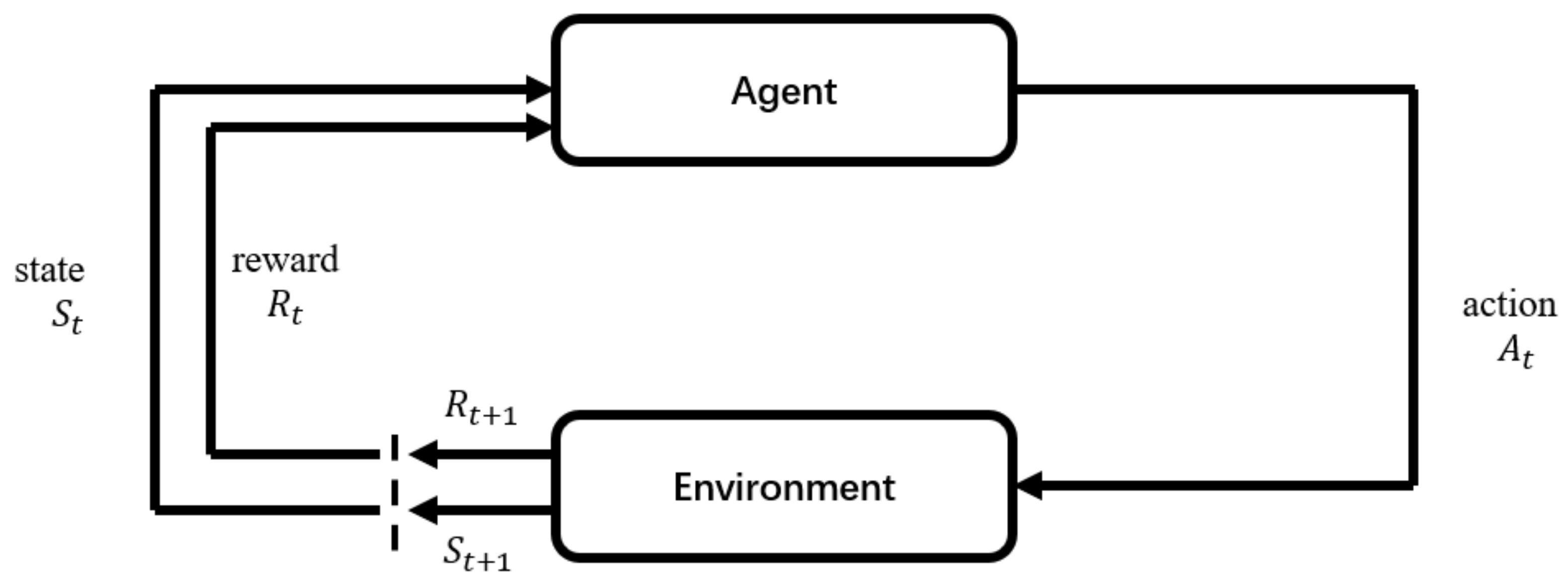
Figure 1.
Reinforcement learning flowchart.

3. Knowledge Distillation

The fundamental principle of knowledge distillation is the specific transmission of the teacher model’s knowledge to the student model. Generally, the teacher model is a large and accurate deep neural network, whereas the student model is its smaller counterpart, often a shallow neural network. During the training process of knowledge distillation, the objective of the student model is to emulate the outputs of the teacher model as closely as possible, thereby achieving model compression while maintaining the performance. The loss function employed in knowledge distillation typically comprises two components. First, the cross-entropy loss is used to compare the outputs of the student model with those of the teacher model, ensuring that the predictions of the student model closely resemble those of the teacher model. Secondly, a temperature parameter T is introduced to control the degree of “softening” of model outputs. The temperature affects the probability distribution of the model output. A relatively high temperature value helps the student model to better obtain knowledge from the teacher model; however, a relatively low temperature value aids in improving the model’s confidence and accuracy, but may cause the student model to be overconfident and disregard the uncertainty of the teacher model in multiple categories. The temperature parameter acts as a balance factor in knowledge distillation, which can adjust the softness and hardness of the model output to better transfer the knowledge of the teacher model and achieve model compression. Figure 2 presents a flowchart of the knowledge distillation process.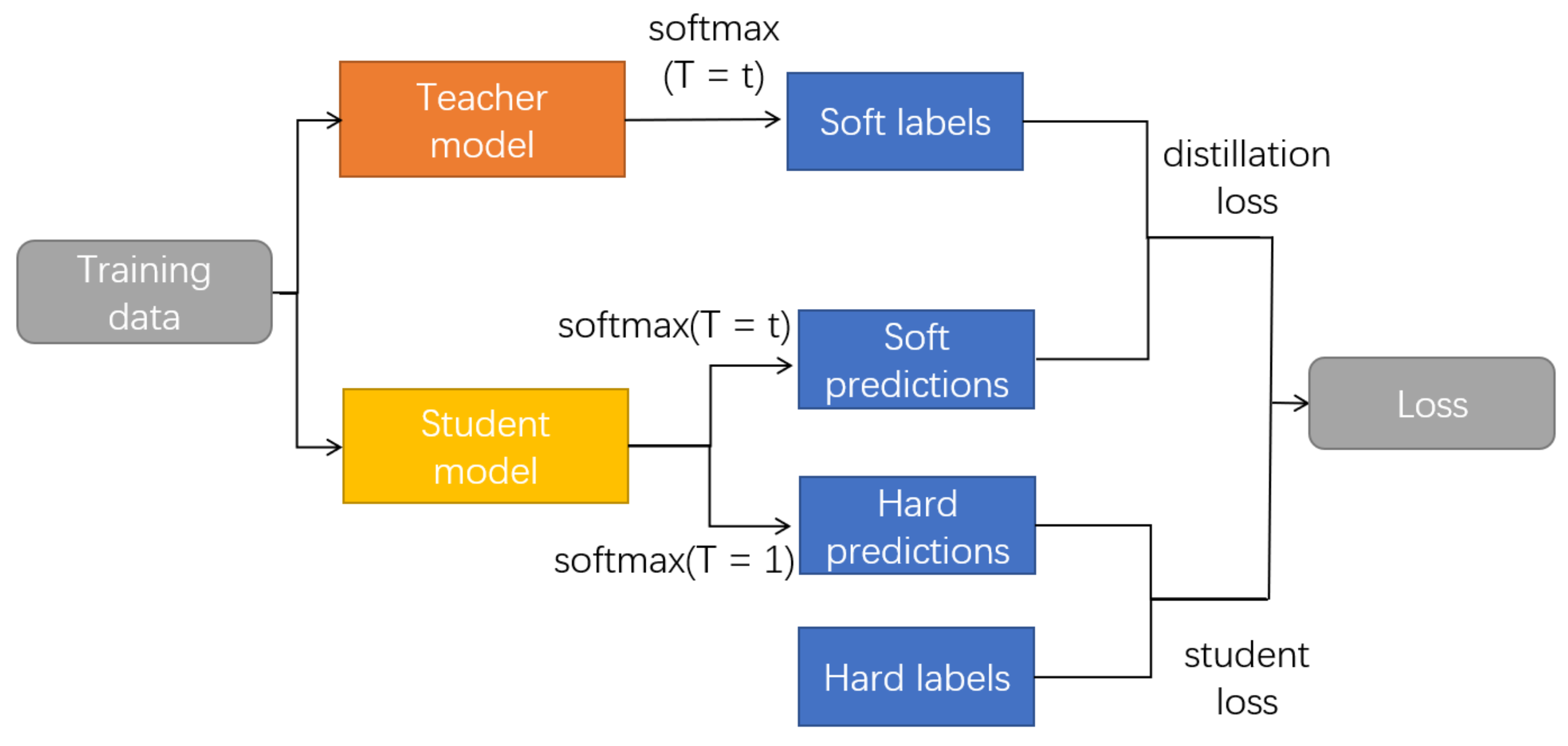
Figure 2.
Flowchart of knowledge distillation.
The original SoftMax function is expressed as follows:
S o f t m a x z i = exp z i ∑ j exp z j
where 𝑧𝑖 is the output value of the i th node and 𝑗 is the number of output nodes.
The SoftMax function after adding temperature “T” is as follows:
S o f t m a x z i = e x p z i ∑ j e x p z j / T

References

  1. Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems 25, South Lake Tahoe, CA, USA, 3–8 December 2012.
  2. Kortylewski, A.; He, J.; Liu, Q.; Yuille, A.L. Compositional convolutional neural networks: A deep architecture with innate robustness to partial occlusion. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 8940–8949.
  3. Kim, I.; Baek, W.; Kim, S. Spatially attentive output layer for image classification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 9533–9542.
  4. Guo, C.; Fan, B.; Zhang, Q.; Xiang, S.; Pan, C. Augfpn: Improving multi-scale feature learning for object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 12595–12604.
  5. Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. In Proceedings of the Advances in Neural Information Processing Systems 28, Montreal, QC, Canada, 7–12 December 2015.
  6. Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the Advances in Neural Information Processing Systems 27, Montreal, QC, Canada, 8–13 December 2014.
  7. Han, S.; Pool, J.; Tran, J.; Dally, W. Learning both weights and connections for efficient neural network. In Proceedings of the Advances in Neural Information Processing Systems 28, Montreal, QC, Canada, 7–12 December 2015.
  8. Guo, Y.; Yao, A.; Chen, Y. Dynamic network surgery for efficient dnns. In Proceedings of the Advances in Neural Information Processing Systems 29, Barcelona, Spain, 5–10 December 2016.
  9. Molchanov, P.; Tyree, S.; Karras, T.; Aila, T.; Kautz, J. Pruning Convolutional Neural Networks for Resource Efficient Inference. arXiv 2016, arXiv:1611.06440.
  10. Luo, J.; Wu, J.; Lin, W. Thinet: A filter level pruning method for deep neural network compression. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 5058–5066.
  11. Vanhoucke, V.; Senior, A.; Mao, M.Z. Improving the speed of neural networks on CPUs. In Proceedings of the NIPS 2011 Workshop on Deep Learning and Unsupervised, Granada, Spain, 12–17 December 2011; Academic Press: Cambridge, MA, USA, 2011.
  12. Hwang, K.; Sung, W. Fixed-point feedforward deep neural network design using weights+ 1, 0, and −1. In Proceedings of the 2014 IEEE Workshop on Signal Processing Systems (SiPS), Belfast, UK, 20–22 October 2014; pp. 1–6.
  13. Rastegari, M.; Ordonez, V.; Redmon, J.; Farhadi, A. Xnor-net: Imagenet classification using binary convolutional neural networks. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 525–542.
  14. Courbariaux, M.; Hubara, I.; Soudry, D.; El-Yaniv, R.; Bengio, Y. Binarized Neural Networks: Training Deep Neural Networks with Weights and Activations Constrained to +1 or −1. arXiv 2016, arXiv:1602.02830.
  15. Zhou, S.; Wu, Y.; Ni, Z.; Zhou, X.; Wen, H.; Zou, Y. Dorefa-Net: Training Low Bitwidth Convolutional Neural Networks with Low Bitwidth Gradients. arXiv 2016, arXiv:1606.06160.
  16. Hinton, G.; Vinyals, O.; Dean, J. Distilling the Knowledge in a Neural Network. arXiv 2015, arXiv:1503.02531.
  17. Zhang, Y.; Xiang, T.; Hospedales, T.M.; Lu, H. Deep mutual learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 4320–4328.
  18. Romero, A.; Ballas, N.; Kahou, S.E.; Chassang, A.; Gatta, C.; Bengio, Y. Fitnets: Hints for Thin Deep Nets. arXiv 2014, arXiv:1412.6550.
  19. Park, W.; Kim, D.; Lu, Y.; Cho, M. Relational knowledge distillation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 3967–3976.
  20. Denton, E.L.; Zaremba, W.; Bruna, J.; LeCun, Y. Exploiting linear structure within convolutional networks for efficient evaluation. In Proceedings of the Advances in Neural Information Processing Systems 27, Montreal, QC, Canada, 8–13 December 2014.
  21. Han, S.; Mao, H.; Dally, W.J. Deep Compression: Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman Coding. arXiv 2015, arXiv:1510.00149.
  22. Lebedev, V.; Ganin, Y.; Rakhuba, M.; Oseledets, I.; Lempitsky, V. Speeding-up Convolutional Neural Networks Using Fine-Tuned Cp-Decomposition. arXiv 2014, arXiv:1412.6553.
  23. Kim, Y.D.; Park, E.; Yoo, S.; Choi, T.; Yang, L.; Shin, D. Compression of Deep Convolutional Neural Networks for Fast and Low Power Mobile Applications. arXiv 2015, arXiv:1511.06530.
  24. Iandola, F.N.; Han, S.; Moskewicz, M.W.; Ashraf, K.; Dally, W.J.; Keutzer, K. SqueezeNet: AlexNet-Level Accuracy with 50× Fewer Parameters and <0.5 MB Model Size. arXiv 2016, arXiv:1602.07360.
  25. Zhang, X.; Zhou, X.; Lin, M.; Sun, J. Shufflenet: An extremely efficient convolutional neural network for mobile devices. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6848–6856.
  26. Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient Convolutional Neural Networks for Mobile Vision Applications. arXiv 2017, arXiv:1704.04861.
  27. Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4510–4520.
  28. Zhao, S.; Zhou, L.; Wang, W.; Cai, D.; Lam, T.L.; Xu, Y. Toward better accuracy-efficiency trade-offs: Divide and co-training. IEEE Trans. Image Process. 2022, 31, 5869–5880.
  29. Gordon, A.; Eban, E.; Nachum, O.; Chen, B.; Wu, H.; Yang, T.-J.; Choi, E. Morphnet: Fast & simple resource-constrained structure learning of deep networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1586–1595.
  30. He, Y.; Lin, J.; Liu, Z.; Wang, H.; Li, L.-J.; Han, S. Amc: Automl for model compression and acceleration on mobile devices. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 784–800.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/)
ScholarVision Creations
Feedback