You're using an outdated browser. Please upgrade to a modern browser for the best experience.
Please note this is a comparison between Version 2 by Camila Xu and Version 1 by Ming Wang.
Downsampling, which aims to improve computational efficiency by reducing the spatial resolution of feature maps, is a critical operation in neural networks. Upsampling also plays an important role in neural networks. It is often used for image super-resolution, segmentation, and generation tasks via the reconstruction of high-resolution feature maps during the decoding stage in the neural network.
- model lightweighting
- information-retaining downsampling
- feature slicing
- depthwise separable convolution
1. Introduction
In recent years, deep learning [1] has achieved remarkable success in various computer vision (CV) tasks, such as image classification [2], object detection [3,4][3][4], and semantic segmentation [5]. However, deep learning (DL) models often suffer from heavy computational burdens due to large numbers of parameters and high-dimensional input data, limiting their practical applications [6]. In particular, the proliferation of smart devices and IoT (Internet of Things) sensors has given rise to a pressing need for edge computing [7] as edge computing enables computation near data sources or things. To deploy DL models on resource-limited edge devices, reducing model complexity has become a priority [8,9][8][9]. Various techniques have been proposed for reducing the complexity of DL models, among which downsampling plays a crucial role [10]. However, most existing downsampling methods tend to lose some detailed information [11]. Thus, it remains a challenging problem to design a lightweight and efficient downsampling component which can retain more semantic and detailed information with lower algorithmic complexity.
In many computer vision tasks, neural network downsampling is a crucial technique that is used to reduce the spatial resolution of the feature map [11,12][11][12]. It can effectively reduce the computational and memory requirements of the network and expand the receptive field while retaining important information for subsequent processing [13]. It reduces the spatial resolution by proportionally scaling down the width and height of feature maps, which can be achieved by selecting a subset of features or by aggregating the features in local regions. Downsampling can help to regularize the network and prevent overfitting by reducing the number of parameters and introducing some degree of spatial invariance [14]. It can improve the efficiency of the neural network in processing large-scale complex data, such as remote sensing images and videos, and enable the DL models to operate on resource-limited devices [15]. Pooling or subsampling of feature maps, such as Max Pooling or Strided Convolution, is a common downsampling operation in the neural network [16]. However, most of the methods condense regional features to a single output, which suffers from several challenges, such as information loss and spatial bias [11]. For instance, Max Pooling only retains the most distinguishable features [17], and subsampling picks a portion of features randomly or according to rules [18[18][19],19], while the slicing adopted in this work utilizes the full information in the input feature map, as shown in Figure 1. Therefore, the research on neural network downsampling is still an active area where there is space for optimization, and more efficient methods need be developed for better retaining feature information.
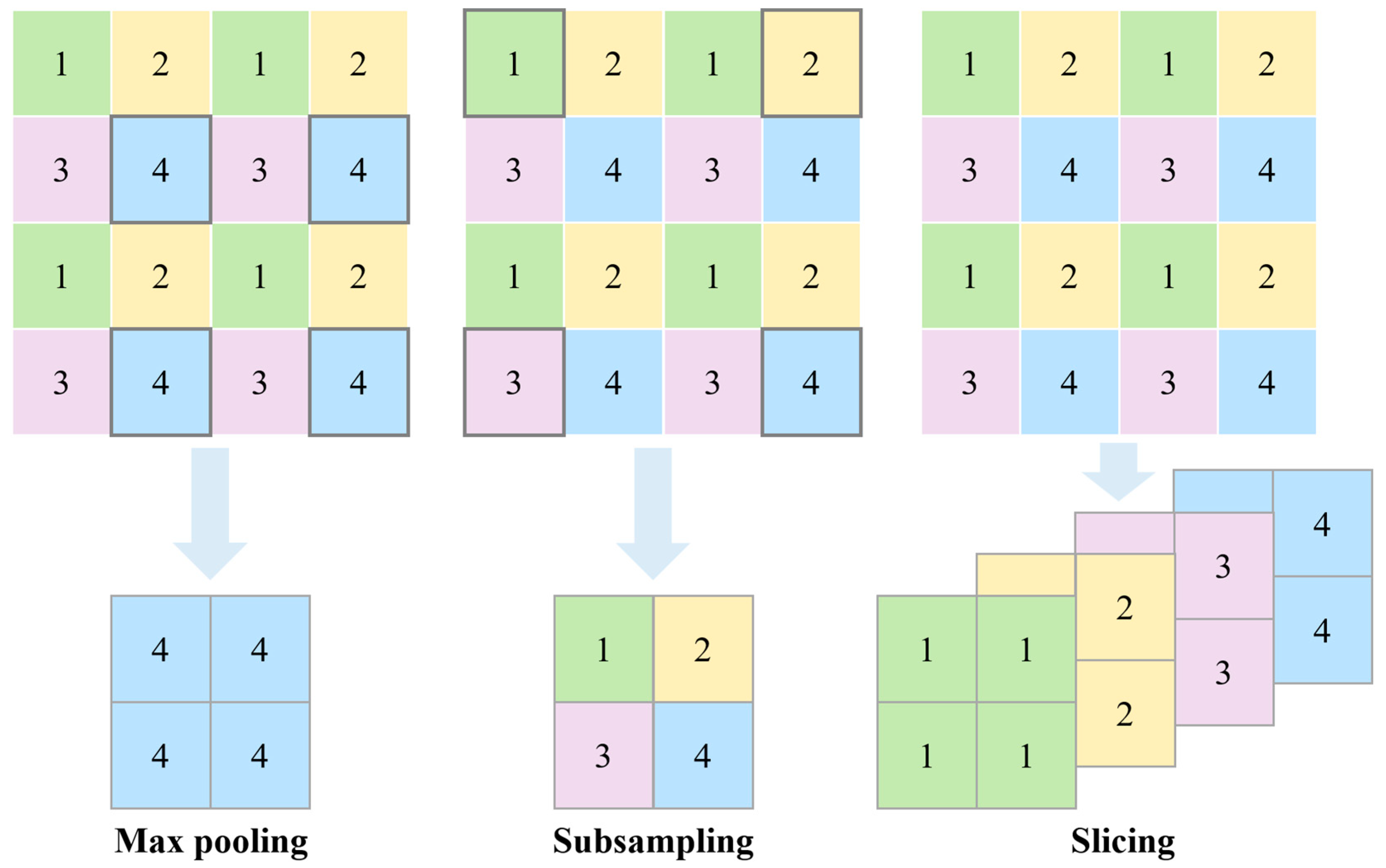
Figure 1.
Feature information retained by different downsampling methods.
Upsampling also plays an important role in neural networks. It is often used for image super-resolution [20], segmentation [21], and generation [22] tasks via the reconstruction of high-resolution feature maps during the decoding stage in the neural network [23]. The main upsampling methods include interpolation-based upsampling such as the Nearest Neighbor, Bilinear, and Bicubic Interpolation methods [24] and the Transposed Convolution [25] and Sub-Pixel Convolutional [26] methods. The simplest and fastest algorithm is Nearest Neighbor sampling in which each pixel is copied in four copies to a 2 × 2 neighborhood; however, jagged edges are often introduced [27]. The Bilinear and Bicubic Interpolation methods calculate new pixel values via the weighted averaging of the nearest pixels in the original image, providing smoother results than Nearest Neighbor Upsampling yet still introducing some blurring [28]. Transposed Convolution, also known as deconvolution or fractionally strided convolution, is the reverse operation of convolution. It produces high-quality results with an expensive computational burden [29]. Sub-Pixel Convolutional Upsampling rearranges the feature maps via a periodic shuffling operator to increase the spatial resolution [26]. It is fast and computationally efficient; however, it may lead to some artifacts. Many existing downsampling techniques are often combined with the above upsampling methods as it is difficult to implement an inverse transform for generating low-dimensional spatial features [11].
2. Downsampling in Neural Networks
To reduce model complexity, researchers have developed various downsampling methods that are tailored to specific tasks and architectures, including pooling-based [17[17][19],19], subsampling-based [16,30][16][30], patch-based [31[31][32],32], and learnable pooling [19,33][19][33] methods. In the early stages of neural network development, Maximum Pooling or Average Pooling were commonly adopted to achieve downsampling by taking the maximum or average value within a local window. These methods are fast and memory-efficient, yet t room for improvement remains in terms of information retention [11]. Some methods that combine Max and Average Pooling, such as Mixed Pooling [34], exhibit better performance compared to a single method. Unlike Maximum Pooling, Average Pooling, and their variants, SoftPool exponentially weights the activations using Softmax (normalized exponential function) kernels to retain feature information [12]. Wu et al. [35] proposed pyramid pooling for the transformer architecture; pyramid pooling which applies different scales of average pooling layers to generate pyramid feature maps, thus capturing powerful contextual features. There are also pooling methods that are designed to enhance the generalization of a model. For example, Fractional Pooling [36], S3Pool [13], and Stochastic Pooling [30] can prevent overfitting by taking random samples in the pooling region. However, most pooling-based methods are hand-crafted nonlinear mappings which usually employ fixed, unlearnable prior knowledge [37]. Nonlinear mapping can also be generated by overlaying complex convolutional layers and activation functions in a deep neural network (DNN) [16]. When the network is shallow, pooling has some advantages. When the network goes deeper, multi-layer stacked convolution can learn better nonlinearity than pooling. It can also achieve better results [38]. Therefore, Strided Convolution, which reduces spatial dimensionality by adjusting the stride to skip some pixels in the feature map, is generally used for downsampling in convolutional neural networks at present [16]. Pooling and Stride Convolution have the advantage of extracting stronger semantic features, although at the cost of losing some detailed information [39]. In contrast, the features extracted via passthrough downsampling [40] have less semantic information but retain more detailed information. In transformer-based networks, patch-based downsampling is generally adopted [31,32][31][32]. Patch merging is a method of reducing the number of tokens in transformer architectures which concatenates the features of each group of 2 × 2 neighboring patches and extracts the features with a linear layer [32]. Patch-based methods perform poorly at capturing fine spatial structures and details, like edges and texture [41]. Li et al. [42] stacked the results of the Discrete Wavelet Transform in the channel dimension instead of directly stacking patches to prevent spatial domain distortion. Moreover, Lu et al. [43] proposed a Robust Feature Downsampling Module by combining various techniques such as slice, Max Pooling, and group convolution, achieving satisfactory results in remote sensing visual tasks. In recent years, learnable weights were gradually introduced into some advanced downsampling methods. Saeedan et al. [19] proposed Detail Preserving Pooling methods that use learnable weights to emphasize spatial changes and preserve edges and texture details. Gao et al. [33] proposed Local Importance-Based Pooling to retain important features based on weights learned by a local attention mechanism. Ma and Gu et al. [44] proposed spatial attention pooling to learn feature weights and refine local features. Hesse et al. [45] introduced a Content-Adaptive Downsampling method that downsamples only the non-critical regions learned by a network, effectively preserving detailed information in the regions of interest. Recently, other studies proposed bi-directional pooling operations that can support both downsampling and upsampling operations, such as Liftpool [46] and AdaPool [11]. Liftpool decomposes the input into multiple sub-bands carrying different frequency information during downsampling and enables inverse recovery during upsampling [46]. AdaPool uses two groups of pooling kernels to better retain the details of the original feature, and its learned weights can be used as prior knowledge for upsampling [11]. These improved downsampling methods have demonstrated good performance gains, yet most of them still inevitably lose some feature information in the downsampling process.3. Depthwise Separable Convolution
Depthwise separable convolution (DSConv) [47] has gained significant attention in recent years due to its effectiveness at reducing the computational cost of convolutional layers in neural networks [48,49][48][49]. An early work was proposed by Chollet in the Xception model [44]. It replaced traditional Inception modules with DSConv and showed advanced performance on the ImageNet dataset with fewer parameters. Another remarkable work on DSConv is MobileNet, which builds faster and more efficient lightweight DNNs for mobile and embedded vision applications using DSConv [50]. In addition, several studies integrated and improved DSConv. Drossos et al. [51] combined DSConv and dilated convolutions for sound event detection. ShuffleNet uses channel shuffle to reduce computational costs in DSConv while maintaining or improving accuracy [52]. Recently, a depthwise separable convolution attention module was proposed to focus on important information and capture the relationships of channels and spatial positions [53]. Compared to standard convolutional layers, DSConv can significantly reduce the computational cost and memory requirements of a network while maintaining competitive model performance [54,55][54][55]. This makes it a popular choice in modern neural network architectures, especially for mobile and embedded devices with limited computational resources [56]. Overall, the above studies demonstrate the effectiveness of DSConv in terms of saving computational resources, as well as the potential ability to further improve model performance by combining DSConv with other techniques.References
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444.
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778.
- He, K.; Gkioxari, G.; Dollar, P.; Girshick, R. Mask R-CNN. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2961–2969. Available online: https://openaccess.thecvf.com/content_iccv_2017/html/He_Mask_R-CNN_ICCV_2017_paper.html (accessed on 20 October 2023).
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788.
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015; Navab, N., Hornegger, J., Wells, W., Frangi, A., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 234–241.
- Sinha, R.K.; Pandey, R.; Pattnaik, R. Deep Learning for Computer Vision Tasks: A review. arXiv 2018, arXiv:1804.03928.
- Shi, W.; Cao, J.; Zhang, Q.; Li, Y.; Xu, L. Edge Computing: Vision and Challenges. IEEE Internet Things J. 2016, 3, 637–646.
- Shen, S.; Li, R.; Zhao, Z.; Liu, Q.; Liang, J.; Zhang, H. Efficient Deep Structure Learning for Resource-Limited IoT Devices. In Proceedings of the GLOBECOM 2020–2020 IEEE Global Communications Conference, Taipei, Taiwan, 7–11 December 2020; pp. 1–6.
- Xie, Y.; Guo, Y.; Mi, Z.; Yang, Y.; Obaidat, M.S. Edge-Assisted Real-Time Instance Segmentation for Resource-Limited IoT Devices. IEEE Internet Things J. 2023, 10, 473–485.
- Voulodimos, A.; Doulamis, N.; Doulamis, A.; Protopapadakis, E. Deep Learning for Computer Vision: A Brief Review. Comput. Intell. Neurosci. 2018, 2018, e7068349.
- Stergiou, A.; Poppe, R. AdaPool: Exponential Adaptive Pooling for Information-Retaining Downsampling. IEEE Trans. Image Process. 2023, 32, 251–266.
- Stergiou, A.; Poppe, R.; Kalliatakis, G. Refining Activation Downsampling with SoftPool. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 10357–10366. Available online: https://openaccess.thecvf.com/content/ICCV2021/html/Stergiou_Refining_Activation_Downsampling_With_SoftPool_ICCV_2021_paper.html (accessed on 20 October 2023).
- Zhai, S.; Wu, H.; Kumar, A.; Cheng, Y.; Lu, Y.; Zhang, Z.; Feris, R. S3Pool: Pooling with Stochastic Spatial Sampling. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4970–4978. Available online: https://openaccess.thecvf.com/content_cvpr_2017/html/Zhai_S3Pool_Pooling_With_CVPR_2017_paper.html (accessed on 20 October 2023).
- Akhtar, N.; Ragavendran, U. Interpretation of intelligence in CNN-pooling processes: A methodological survey. Neural Comput. Appl. 2020, 32, 879–898.
- Ajani, T.S.; Imoize, A.L.; Atayero, A.A. An Overview of Machine Learning within Embedded and Mobile Devices–Optimizations and Applications. Sensors 2021, 21, 4412.
- Ayachi, R.; Afif, M.; Said, Y.; Atri, M. Strided Convolution Instead of Max Pooling for Memory Efficiency of Convolutional Neural Networks. In Proceedings of the 8th International Conference on Sciences of Electronics, Technologies of Information and Telecommunications (SETIT’18), Genoa, Italy, 18–20 December 2018; Bouhlel, M., Rovetta, S., Eds.; Springer International Publishing: Cham, Switzerland, 2020; Volume 1, pp. 234–243.
- Devi, N.; Borah, B. Cascaded pooling for Convolutional Neural Networks. In Proceedings of the 2018 Fourteenth International Conference on Information Processing (ICINPRO), Bangalore, India, 21–23 December 2018; pp. 1–5.
- Kuen, J.; Kong, X.; Lin, Z.; Wang, G.; Yin, J.; See, S.; Tan, Y.-P. Stochastic Downsampling for Cost-Adjustable Inference and Improved Regularization in Convolutional Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7929–7938. Available online: https://openaccess.thecvf.com/content_cvpr_2018/html/Kuen_Stochastic_Downsampling_for_CVPR_2018_paper.html (accessed on 20 October 2023).
- Saeedan, F.; Weber, N.; Goesele, M.; Roth, S. Detail-Preserving Pooling in Deep Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 9108–9116. Available online: https://openaccess.thecvf.com/content_cvpr_2018/html/Saeedan_Detail-Preserving_Pooling_in_CVPR_2018_paper.html (accessed on 20 October 2023).
- Yan, Y.; Liu, C.; Chen, C.; Sun, X.; Jin, L.; Peng, X.; Zhou, X. Fine-Grained Attention and Feature-Sharing Generative Adversarial Networks for Single Image Super-Resolution. IEEE Trans. Multimed. 2022, 24, 1473–1487.
- Lin, G.; Milan, A.; Shen, C.; Reid, I. RefineNet: Multi-path Refinement Networks for High-Resolution Semantic Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5168–5177.
- Gragnaniello, D.; Cozzolino, D.; Marra, F.; Poggi, G.; Verdoliva, L. Are GAN Generated Images Easy to Detect? A Critical Analysis of the State-Of-The-Art. In Proceedings of the 2021 IEEE International Conference on Multimedia and Expo (ICME), Shenzhen, China, 5–9 July 2021; pp. 1–6.
- Li, Y.; Cai, W.; Gao, Y.; Li, C.; Hu, X. More than Encoder: Introducing Transformer Decoder to Upsample. In Proceedings of the 2022 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Las Vegas, NV, USA, 6–8 December 2022; pp. 1597–1602.
- Fadnavis, S. Image Interpolation Techniques in Digital Image Processing: An Overview. Int. J. Eng. Res. Appl. 2014, 4, 2248–962270.
- Zeiler, M.D.; Taylor, G.W.; Fergus, R. Adaptive deconvolutional networks for mid and high level feature learning. In Proceedings of the 2011 IEEE International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2018–2025.
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1874–1883. Available online: https://www.cv-foundation.org/openaccess/content_cvpr_2016/html/Shi_Real-Time_Single_Image_CVPR_2016_paper.html (accessed on 20 October 2023).
- Olivier, R.; Hanqiang, C. Nearest Neighbor Value Interpolation. Int. J. Adv. Comput. Sci. Appl. 2012, 3, 25–30.
- Hwang, J.W.; Lee, H.S. Adaptive Image Interpolation Based on Local Gradient Features. IEEE Signal Process. Lett. 2004, 11, 359–362.
- Zhong, F.; Li, M.; Zhang, K.; Hu, J.; Liu, L. DSPNet: A low computational-cost network for human pose estimation. Neurocomputing 2021, 423, 327–335.
- Zeiler, M.D.; Fergus, R. Stochastic Pooling for Regularization of Deep Convolutional Neural Networks. arXiv 2013, arXiv:1301.3557.
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image Is Worth 16 × 16 Words: Transformers for Image Recognition at Scale. arXiv 2021, arXiv:2010.11929. Available online: http://arxiv.org/abs/2010.11929 (accessed on 20 October 2023).
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer Using Shifted Windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 10012–10022. Available online: https://openaccess.thecvf.com/content/ICCV2021/html/Liu_Swin_Transformer_Hierarchical_Vision_Transformer_Using_Shifted_Windows_ICCV_2021_paper.html (accessed on 20 October 2023).
- Gao, Z.; Wang, L.; Wu, G. LIP: Local Importance-Based Pooling. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3355–3364. Available online: https://openaccess.thecvf.com/content_ICCV_2019/html/Gao_LIP_Local_Importance-Based_Pooling_ICCV_2019_paper.html (accessed on 20 October 2023).
- Yu, D.; Wang, H.; Chen, P.; Wei, Z. Mixed Pooling for Convolutional Neural Networks. In Rough Sets and Knowledge Technology; Miao, D., Pedrycz, W., Ślȩzak, D., Peters, G., Hu, Q., Wang, R., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 364–375.
- Wu, Y.-H.; Liu, Y.; Zhan, X.; Cheng, M.-M. P2T: Pyramid Pooling Transformer for Scene Understanding. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 12760–12771.
- Graham, B. Fractional Max-Pooling. arXiv 2015.
- Sun, M.; Song, Z.; Jiang, X.; Pan, J.; Pang, Y. Learning Pooling for Convolutional Neural Network. Neurocomputing 2017, 224, 96–104.
- Montavon, G.; Lapuschkin, S.; Binder, A.; Samek, W.; Müller, K.-R. Explaining nonlinear classification decisions with deep Taylor decomposition. Pattern Recognit. 2017, 65, 211–222.
- Liu, Y.; Gross, L.; Li, Z.; Li, X.; Fan, X.; Qi, W. Automatic Building Extraction on High-Resolution Remote Sensing Imagery Using Deep Convolutional Encoder-Decoder with Spatial Pyramid Pooling. IEEE Access 2019, 7, 128774–128786.
- Redmon, J.; Farhadi, A. YOLO9000: Better, Faster, Stronger. arXiv 2016, arXiv:1612.08242. Available online: http://arxiv.org/abs/1612.08242 (accessed on 20 October 2023).
- Khan, S.; Naseer, M.; Hayat, M.; Zamir, S.W.; Khan, F.S.; Shah, M. Transformers in Vision: A Survey. ACM Comput. Surv. 2022, 54, 1–41.
- Li, Y.; Liu, Z.; Wang, H.; Song, L. A Down-sampling Method Based on The Discrete Wavelet Transform for CNN Classification. In Proceedings of the 2023 2nd International Conference on Big Data, Information and Computer Network (BDICN), Xishuangbanna, China, 6–8 January 2023; pp. 126–129.
- Lu, W.; Chen, S.-B.; Tang, J.; Ding, C.H.Q.; Luo, B. A Robust Feature Downsampling Module for Remote-Sensing Visual Tasks. IEEE Trans. Geosci. Remote. Sens. 2023, 61, 1–12.
- Ma, J.; Gu, X. Scene image retrieval with siamese spatial attention pooling. Neurocomputing 2020, 412, 252–261.
- Hesse, R.; Schaub-Meyer, S.; Roth, S. Content-Adaptive Downsampling in Convolutional Neural Networks. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Vancouver, BC, Canada, 17–24 June 2023; pp. 4544–4553.
- Zhao, J.; Snoek, C.G.M. LiftPool: Bidirectional ConvNet Pooling. arXiv 2021, arXiv:2104.00996.
- Chollet, F. Xception: Deep Learning with Depthwise Separable Convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1251–1258. Available online: https://openaccess.thecvf.com/content_cvpr_2017/html/Chollet_Xception_Deep_Learning_CVPR_2017_paper.html (accessed on 20 October 2023).
- Kaiser, L.; Gomez, A.N.; Chollet, F. Depthwise Separable Convolutions for Neural Machine Translation. arXiv 2017, arXiv:1706.03059.
- Liu, B.; Zou, D.; Feng, L.; Feng, S.; Fu, P.; Li, J. An FPGA-Based CNN Accelerator Integrating Depthwise Separable Convolution. Electronics 2019, 8, 281.
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications. arXiv 2017, arXiv:1704.04861.
- Drossos, K.; Mimilakis, S.I.; Gharib, S.; Li, Y.; Virtanen, T. Sound Event Detection with Depthwise Separable and Dilated Convolutions. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–7.
- Zhang, X.; Zhou, X.; Lin, M.; Sun, J. ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6848–6856. Available online: https://openaccess.thecvf.com/content_cvpr_2018/html/Zhang_ShuffleNet_An_Extremely_CVPR_2018_paper.html (accessed on 20 October 2023).
- Liu, F.; Xu, H.; Qi, M.; Liu, D.; Wang, J.; Kong, J. Depth-Wise Separable Convolution Attention Module for Garbage Image Classification. Sustainability 2022, 14, 3099.
- Pilipovic, R.; Bulic, P.; Risojevic, V. Compression of convolutional neural networks: A short survey. In Proceedings of the 2018 17th International Symposium INFOTEH-JAHORINA (INFOTEH), East Sarajevo, Bosnia and Herzegovina, 21–23 March 2018; pp. 1–6.
- Winoto, A.S.; Kristianus, M.; Premachandra, C. Small and Slim Deep Convolutional Neural Network for Mobile Device. IEEE Access 2020, 8, 125210–125222.
- Elordi, U.; Unzueta, L.; Arganda-Carreras, I.; Otaegui, O. How Can Deep Neural Networks Be Generated Efficiently for Devices with Limited Resources? In Articulated Motion and Deformable Objects; Perales, F., Kittler, J., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 24–33.
More
