In machine learning, basically, a computer program is given some tasks to complete; if the computer program’s measured performance on these tasks improves as it obtains more and more experience completing these tasks, it is claimed that the machine has learned from its experience. As a result, the machine makes decisions and predictions according to data. Traditional machine learning has three major segments, namely supervised learning, unsupervised learning, and reinforcement learning. Supervised machine learning is a subset of machine learning in which the algorithm learns using labeled training data. In this method, the model is given input data and labels for the expected outputs. For the model to accurately predict future events or categorize previously unidentified data, it must understand the relationship between inputs and outputs. In other words, when training instances have known labels, and there is consequently the least amount of ambiguity, supervised learning datasets are based on labeled inputs and their corresponding outputs, which seeks to develop a notion for accurately identifying unknown occurrences. On the other hand, Unsupervised machine learning is a sort of machine learning in which the algorithm is tasked with discovering patterns, structures, or groupings within the data on its own after being provided unlabeled data. There are no predetermined output labels to direct the learning process, in contrast to supervised learning. Instead, using methods like clustering or dimensionality reduction, the program looks for inherent relationships or commonalities between the data points. In short, when the training instances do not have labels, and there is consequently the greatest amount of uncertainty, unsupervised learning tries to understand the structure of the underlying patterns of instances. Algorithms for reinforcement learning (RL) use the learning approach by interacting with the environment (sequences of actions, observations, and rewards). Robotics and resource allocation are two areas where RL-based techniques have demonstrated outstanding performance. These have made them one of the most promising prospects for achieving the aim of artificial intelligence (AI), creating autonomous entities that can learn in complex and unknowable contexts [1].

The amount of data required to handle significant problems has grown tremendously in recent years. A considerable amount of labeling work is necessary for large amounts of data. Since weak supervision is typically easier to get, approaches with weak supervision, like MIL, might lessen this load. For instance, object detectors could be trained to utilize web-sourced images and their associated labels as weak supervision instead of manually labeled data sets. Instead of spending money and time on expensive manual annotations, which can be only provided by experts, as the case may be in medical images for which only patient diagnoses are accessible, can be used to train computer-aided diagnosis algorithms; MIL enables the use of partially annotated data to complete the tasks with fewer resources.

The robotics industry, virtual assistants (for example, Google, etc.), video games, pattern recognition, natural language processing (NLP), data mining, traffic forecasting, online public transportation systems (one example is predicting surge prices by the Uber app during peak hours), product recommendation, share market prediction, healthcare diagnosis, online fraud detection, and search engine result prediction and refinement (for example, Google search results) are just a few of the fields where machine learning is used [2].

MIL is a type of weakly supervised learning. Training data are arranged in groupings called bags for multiple-instance learning (MIL), which uses these data. Only complete sets are subject to supervision; the individual labels of the instances contained in the bags are not made available. The research community has given this problem formulation much attention, especially in the last few years when the amount of data required to address major problems has proliferated. A significant amount of labeling work is required due to the large amounts of data. As stated earlier, in MIL, inputs are arranged in bags, and each bag has multiple instances/inputs. A single label is associated with a bag full of instances rather than every single instance. Unlike supervised learning, where all instances have predefined labels, multi-instance learning uses training instances with unknown and ambiguous labels. This arrangement of MIL is gaining popularity because of its flexibility as it leverages weakly/ambiguously annotated data [3].

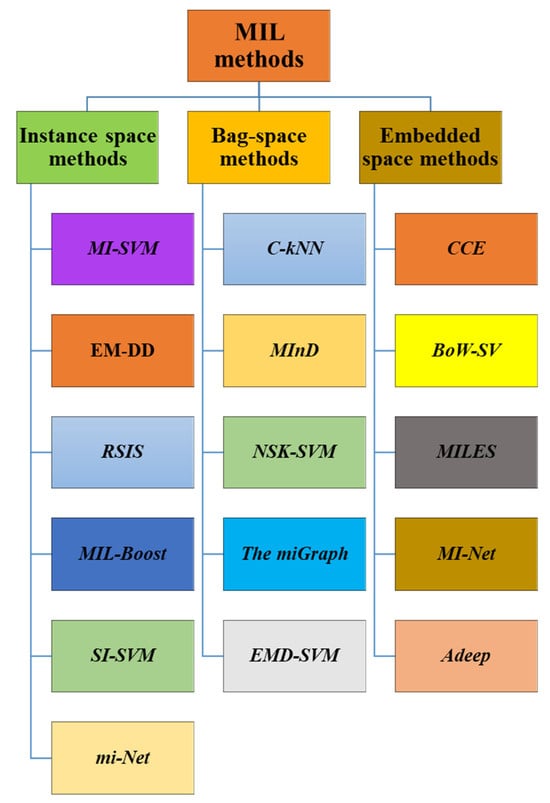
There are multiple types of MIL methods. These categories include Instance-space methods (IS), bag-space (BS), and embedded-space (EB) methods. Depending on how a method uses the knowledge and information that is extracted and exploited from the MI data, they are classified. These MIL methods are shown in Figure 1. In Instance space methods, instance-level learning takes place, where f(x) is trained to distinguish between positive and negative bag instances. Instance-level scores calculated by f(x) are then merged to produce a classifier for bag-level F(X), in line with a plausible MI assumption. In order to avoid ignoring more general properties of the entire bag, IS approaches only take into account the attributes of specific instances. The BS and ES techniques, in contrast, regard every other bag as a complete unit and train F(X) using the global bag-level data. While ES methods use a mapping function to embed multiple instances of a bag into a single “meta” instance defined on a new feature space, With the help of distance-based classifiers like k-Nearest Neighbors (kNN) and Support Vector Machine (SVM), BS techniques try to determine how similar or far apart each pair of bags are from one another and predict the labels of the bags directly ^[4][29]. These are not MIL techniques in and of themselves, but this kind of approach has been utilized as a reference point in several works ^[5][6][7][30,31,32] to give an idea of the relevance of employing MIL methods instead of typical supervised algorithms. In these techniques, the bag label is allocated to each instance, and bag information is ignored. Each case receives a label from the classifier during the test, and a bag is considered positive if it has no less than one positive instance. In the case of SI-SVM-TH (Single Instance Support Vector Machine with Threshold), the overall positive instances found are compared to an optimized threshold using the training data.

2. Instance Space Methods

IS methods disregard bag architecture and create classifiers at the level of instances after propagating bag labels to the associated instances. Then, in order to create bag labels, instance predictions are aggregated based on an appropriate MI assumption, such as the standard assumption, the collective assumption (e.g., the sum or average of individual instance predictions in a bag), and the maximum or the minimum of the instance prediction ^[8][9]. Some IS methods are mentioned below.

2.1. MI-SVM (Multiple Instance Support Vector Machine) and mi-SVM (Mixture of Multiple Instance Support Vector Machines)

To work in the MI setting, both MI-SVM (Multiple Instance Support Vector Machine) and mi-SVM (mixture of Multiple Instance Support Vector Machines) ^[9][33] techniques are extensions of SVM, sometimes known as a maximum-margin classifier. SVM identifies a hyperplane for binary classification that produces the greatest margin (or separation) between the two classes. All instances in negative bags have negative labels using mi-SVM, but instances in positive bags have unknown labels. A soft-margin criterion defined at the instance level is then maximized collectively over the hyperplanes and unobserved instance labels in positive bags, resulting in all instances in each negative bag being located on one side of the hyperplane and a minimum of one instance in each positive bag being positioned on the other. An SVM classifier is created with each iteration, and instance labels are changed. Once the imputed labels have stopped changing, the SVM is retrained to further refine the decision boundary using the freshly assigned labels. The margin of a positive bag is defined by the margin of the “most positive” instance, whereas the margin of a negative bag is defined by the “least negative” instance. Instead of maximizing the instance-level margin, MI-SVM represents each bag by one representative instance of the bag and maximizes the bag-level margin. When the representative instance does not vary in each bag, an SVM classifier is generated. The authors argued that mi-SVM is superior if one wants to perform an accurate instance classification; otherwise, MI-SVM is more suitable.

2.2. EM-DD (Expectation–Maximization Diverse Density)

Expectation–Maximization Diverse Density (DD) algorithm ^[10][34] is an extension of the Diverse Density (DD) ^[11][14] algorithm that looks for a point in the feature space with the highest DD that is as close to a number of diverse positive bags as is feasible while being as far away from the negative bags as is feasible given the neighborhood’s proportion of instances of the bag. The maximum of the DD function is found using the Expectation-Maximization approach by EM DD. The classification is dependent on how far away this maximum point is.

2.3. RSIS (Random Subspace Instance Selection)

This method detects the witnesses in positive bags statistically by employing a technique based on random sub-spacing and clustering introduced in ^[12][13][14][35,36,37]. Training subgroups are sampled by applying the instances’ probabilistic labels to train a set of SVMs.

2.4. MIL-Boost

The technique provided in ^[14][37] was generalized to create the MIL-Boost algorithm ^[15][8]. With the exception of the loss function, which is based on bag classification error, the technique is substantially the same as gradient boosting ^[16][38]. The occurrences are categorized separately, and bag labels are created by combining their labels.

2.5. SI-SVM (Single Instance Support Vector Machine) and SI-kNN (Single Instance k-Nearest Neighbors)

When regular (single-instance) supervised classifiers are trained on MI data using SI-SVM ^[5][30] and SI-kNN [3], the bag-membership knowledge about instances is completely disregarded. The bag label is inherited by every instance in their implementation, and the SVM and kNN classifiers are tailored for the streamlined (single instance) problem.

2.6. mi-Net (Multiple Instance Neural Networks)

Wang et al. ^[17][39] coined the name “mi-Net” to refer to multiple instance neural networks (MINNs), which forecast the likelihood that a specific instance will be positive before combining instance-level probabilities to produce bag-level probabilities using a MIL pooling layer. Let us assume that MINN is composed of L layers. Each instance is first directed toward one of the numerous FC levels that serve as activation levels. After instance-level probabilities are predicted from the last FC layer or the (L-1)th layer of the MINN, the bag-level probability is collected from the last layer for each bag using a MIL pooling function (such as maximum pooling, mean pooling, and log-sum-exp pooling).

3. Bag-Space Methods

Compared to IS methods, which ignore the bag architecture while learning, BS methods learn the distance or similarity among each set of bags. To put it simply, BS techniques use a traditional supervised learning technique, like kNN and SVM, to learn the bag-to-bag connection before employing a suitable distance or kernel function for integrating the bags using their own member instances ^[18][15]. Some common bag-space methods are mentioned below.

3.1. C-kNN (Citation-k-Nearest Neighbors)

CkNN (Citation-kNN) ^[11][14] is a variation of SI-kNN (Single Instance k-Nearest Neighbors) tailored to MI data that determines the distance between two bags using the smallest Hausdorff distance in order to make sure that the estimated distance is resilient to high instance values. C-kNN is based on a two-level voting system that was motivated by the idea of references and citations in research publications. The authors proposed the terms “reference” and “citer,” where references are a given bag’s closest neighbors and citers are bags that view the given bag as their closest neighbor. A bag is classified as positive by employing references and citers collectively if the ratio of positive bags is higher than that of negative bags between its citers and references. Consider a bag that contains C = C+ + C- citers and R = R+ + R- references, where a subscript denotes the bag label. R+ + C+ > R- + C- identifies the target bag as positive in this case. To lessen the likelihood of producing false positives, which occur far more frequently in applications of machine learning than false negatives, the bag is put in the negative class if there is a tie. This algorithm can be modified to carry out instance classification ^[19][40].

3.2. MInD (Multiple Instance Learning with Bag Dissimilarities)

According to MInD ^[20][41], a vector with fields distinct from those of other bags is used to represent each bag in the training data set. These feature vectors are categorized in accordance with a standard supervised classifier, an SVM, in this instance. The publication suggests a number of dissimilarity metrics; however, the mean min provided the best overall performance.

3.3. NSK-SVM (Normalized Set Kernel-SVM)

An expanded version of kernel methods called NSK-SVM ^[21][42] proposes a normalized set kernel (NSK), which is used for machine learning data. The selected instance-level kernel serves as the source for the set kernel, which is particularly defined on bags. Common options include matching kernel, polynomial kernel, and radial basis function kernel. In order to lessen the influence of differing bag sizes, normalization, which is accomplished by the averaged pairwise distances amongst every instance contained in two bags, is essential. The NSK is then used to construct an SVM that can predict bag labels.

3.4. The miGraph

MiGraph ^[22][43] is a proposed method for bag classification by the authors that can take advantage of the relationships between instances by considering them as components of the bag that are interconnected. The observation that was made by Zhou et al. ^[22][43] is what inspired this methodology instances are hardly ever distributed (i.i.d.) independently and identically in a bag. Each bag is represented by a graph in the miGraph method, whose nodes are the instances. If the Gaussian distance across two instances is less than a predetermined threshold (such as the average distance in the bag), then there is an edge between the instances. Because instances may be reliant on one another, the weights they contribute to the bag classification are altered by the cliques visible in the graph. An SVM, along with a graph kernel (built with instance weights), classifies on the basis of between-bag similarity after all bags have been represented by their respective graphs. Utilizing an identity edge matrix (i.e., between any two instances there is no edge) can be useful in handling independent and identical instances.

3.5. EMD-SVM (Earth Mover’s Distance-SVM)

To determine how similar any two bags are (let us say i and i’), the suggested method uses Earth Mover’s Distance (EMD) ^[23][24][44,45]. EMD is a weighted average of the ground distances between all pairs of instances (j, j’), where instance j (j’) is from bag i (i’), and vice versa. In Zhang et al. ^[23][44], the Euclidean distance is used as the ground distance measure, and the weights are obtained by resolving a linear programming issue. The obtained distances are converted to a Gaussian kernel function and then employed in an SVM for bag classification.

4. Embedded Space Methods

Similar to BS approaches, ES methods summarize a bag that only uses a single feature vector to extract information at the level of the bag from machine learning data and then convert a machine learning problem to a standard supervised learning problem. ES techniques, however, emphasize instance embedding ^[18][15]. Some of the embedded space methods are given below.

4.1. CCE (Constructive-Clustering-Based Ensemble)

In order to represent each bag, a Constructive-Clustering-based Ensemble (CCE) ^[25][28] first divides the training sets instances into C clusters using the k-means clustering algorithm. If a bag contains no less than one instance from a cluster of instances named c, the value for the associated cth feature component would be 1; if not, it is 0. An SVM can be designed to classify bags using new bag-level features. It is suggested to train several classifiers on the basis of various clustering findings and assumptions and then aggregate their predictions by a vote of the majority because there are no limits on the choice of C. In this way, CCE makes use of ensemble learning as well. Whenever there is a new bag that is presented for classification, this CCE methodology re-represents it by looking up the clustering results and then supplies the ensemble classifier with the produced feature vectors to predict the label of the bag. Be aware that any other clustering, classification, and ensemble methods in CCE may be used in place of k-means, SVM, and majority voting, respectively.

4.2. BoW-SVM (Bag-of-Words-SVM)

The initial stage in applying a BoW approach is compiling a sample term dictionary. By applying k-means clustering to all of the training cases, this is accomplished using BoW-SVM ^[4][29]. The most similar term found in the dictionary is then used to represent instances. The words’ frequency histograms serve as a representation of bags. An SVM classifies histograms using a kernel designed for histogram comparison.

4.3. MILES (Multiple-Instance Learning via Embedded Instance Selection)

MILES ^[26][46], which stands for Multiple-Instance Learning by Embedded instance Selection, implies that only a portion of instances are in charge of the bag labels. Each bag is mapped into a new feature space during the embedding step using a vector representing the score of similarities among the bags being used at the time and the collection of examples from all the bags. This results in highly dimensional features, even those that are repetitive or ineffective, with the resultant feature space’s dimensionality being equivalent to the overall number of instances, which may be huge. Both choosing significant features and building classifiers can be done simultaneously using SVM with the LASSO penalty ^[27][47]. Additionally, by figuring out how much each instance contributes to the classification of a bag depending on a predetermined threshold, MILES may be used for instance classification.

4.4. MI-Net (Multiple Instance Neural Network)

It is the first MINN (Multiple Instance Neural Network) approach in the ES techniques category. It learns how to represent bags from the features of the instances and then accordingly classifies the bags. In contrast to mi-Net, which concentrates on computing instance-level probabilities. Consider a MINN with L layers; MI-NET’s pooling process, which is based on MIL, compiles all the instances into a single bag and represents it as a single feature vector, which happens in the (L-1)th layer. With a sigmoid activation function, the FC layer (also known as the Lth or the last layer) outputs bag-level probabilities from the input bag representation. In addition to the basic version mentioned above, two MI-Net variations have been proposed ^[17][39], one of which includes deep supervision ^[28][48] and the other of which takes residual connections ^[29][49] into account. Both of these can occasionally increase performance.

4.5. Adeep (Attention-based Deep)

Attention-based Deep MIL (ADeep) ^[30][50] is a MINN approach in addition to mi-Net and MI-Net. It alters the ES technique to improve the understanding by utilizing a cutting-edge multiple-instance learning-based pooling technique that depends on a unique attention mechanism ^[31][51], where each instance is taken as an independent unit. A weighted average of all the instances is calculated and is offered as an alternative to conventional pooling operators like max and mean, which are already specified and untrainable. Instead, a neural network consisting of two layers generates the weights and sums to 1, making them unaffected by how big or small the bag is. Naturally, instances that are more probable to be positive weigh more in the bag than the others, producing outcomes that are easier to interpret. By offering instance weights as a substitute for instance probabilities, ADeep, in this sense, connects the ES technique to the IS technique.