NNetEn is the first entropy measure that is based on artificial intelligence methods. The method modifies the structure of the LogNNet classification model so that the classification accuracy of the MNIST-10 digits dataset indicates the degree of complexity of a given time series. The calculation results of the proposed model are similar to those of existing methods, while the model structure is completely different and provides considerable advantages. An extended version of NNetEn and a Python implementation are proposed in https://doi.org/10.3390/a16050255
- entropy
- time series
- neural network
1. Introduction or History
NNetEn is the first entropy measure that is based on artificial intelligence methods that was introduced by Dr. Andrei Velichko and Dr. Hanif Heidari [1]. An extended version of NNetEn and a Python implementation are proposed in https://doi.org/10.3390/a16050255 .
Measuring the regularity of dynamical systems is one of the hot topics in science and engineering. For example, it is used to investigate the health state in medical science [2][3], for real-time anomaly detection in dynamical networks [4], and for earthquake prediction [5].
Entropy is a thermodynamics concept that measures the molecular disorder in a closed system. This concept is used in nonlinear dynamical systems to quantify the degree of complexity. Entropy is an interesting tool for analyzing time series, as it does not consider any constraints on the probability distribution [6]. Shannon entropy (ShEn) and conditional entropy (ConEn) are the basic measures used for evaluating entropy [7]. ShEn and ConEn measure the amount of information and the rate of information generation, respectively. Based on these measures, other entropy measures have been introduced for evaluating the complexity of time series. For example, Letellier used recurrence plots to estimate ShEn [8]. Permutation entropy (PerEn) is a popular entropy measure that investigates the permutation pattern in time series [9]. Pincus introduced the approximate entropy (ApEn) measure, which is commonly used in the literature [10]. Sample entropy (SaEn) is another entropy measure that was introduced by Richman and Moorman [11]. The ApEn and SaEn measures are based on ConEp. All these methods are based on probability distribution and have shortcomings, such as sensitivity in short-length time series [12], equality in time series [13], and a lack of information related to the sample differences in amplitude [9]. To overcome these difficulties, many researchers have attempted to modify their methods. For example, Azami and Escudero introduced fluctuation-based dispersion entropy to deal with the fluctuations of time series [2]. Letellier used recurrent plots to evaluate Shannon entropy in time series with noise contamination. Watt and Politi investigated the efficiency of the PE method and introduced modifications to speed up the convergence of the method [14]. Deng introduced Deng entropy [15], which is a generalization of Shannon entropy. Martinez-Garcia et al. applied deep recurrent neural networks to approximate the probability distribution of the system outputs [16].
Velichko A. and Heidari H. propose a new method for evaluating the complexity of a time series which has a completely different structure compared to the other methods. It computes entropy directly, without considering or approximating probability distributions. The proposed method is based on LogNNet, an artificial neural network model [17]. Velichko [17] showed a weak correlation between the classification accuracy of LogNNet and the Lyapunov exponent of the time series filling the reservoir. Subsequently, authors found that the classification efficiency is proportional to the entropy of the time series, and this finding led to the development of the proposed method. LogNNet can be used for estimating the entropy of time series, as the transformation of inputs is carried out by the time series, and this affects the classification accuracy. A more complex transformation of the input information, performed by the time series in the reservoir part, results in a higher classification accuracy in LogNNet.
2. Model
To determine entropy, the following main steps should be performed: the LogNNet reservoir matrix should be filled with elements of the studied time series (Figure 1), and then the network should be trained and tested using handwritten MNIST-10 digits in order to determine the classification accuracy.
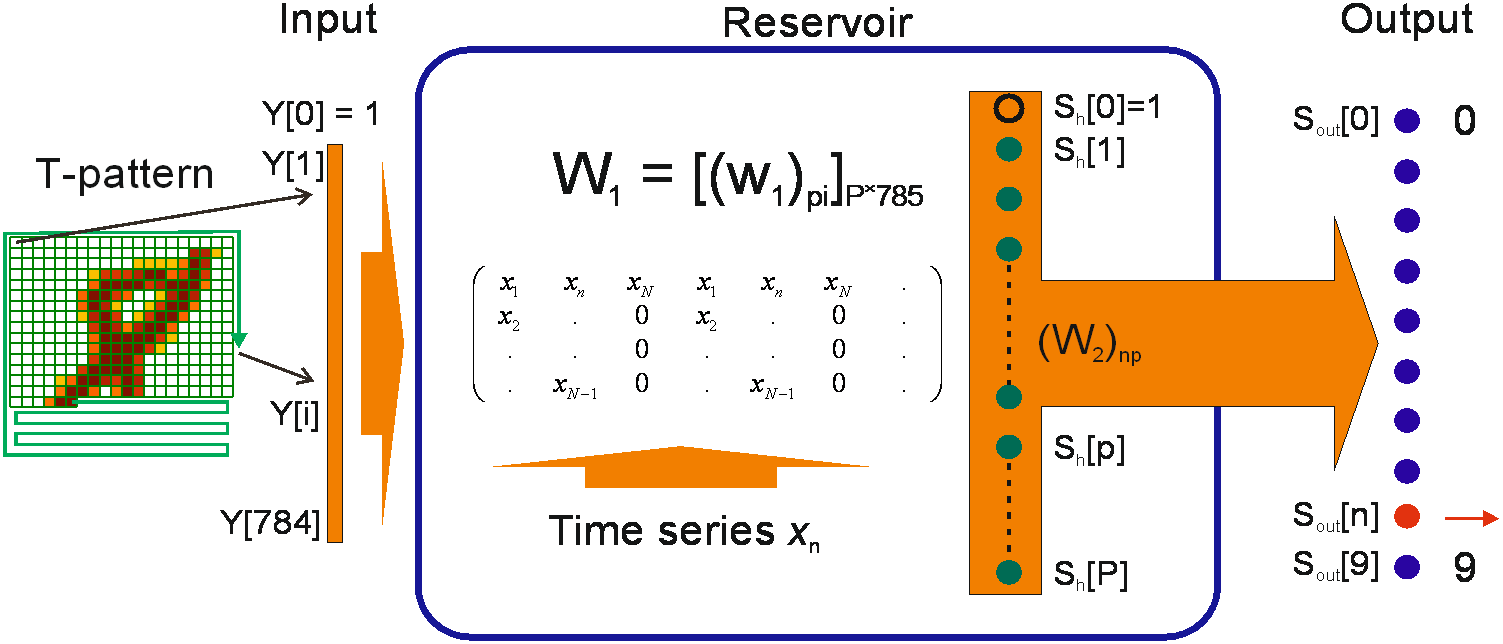
Figure 1. LogNNet architecture for NNetEn calculation.
Accuracy is considered to be the entropy measure and denoted as NNetEn (1).

To validate the method, authors used the well-known chaotic maps, including the logistic (Figure 2), sine, Planck, and Henon maps, as well as random, binary, and constant time series.
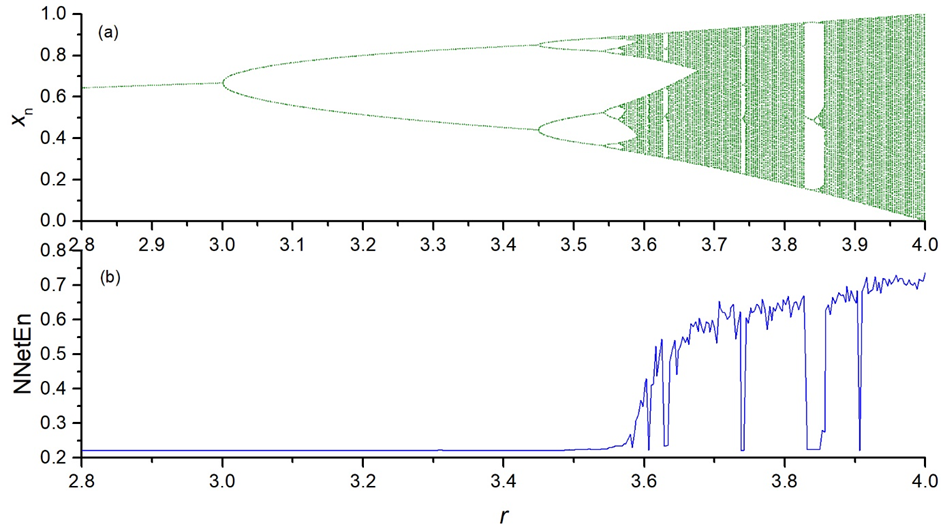
Figure 2. Bifurcation diagrams for logistic map ((a); the dependence of NNetEn on the parameter r (number of epochs is 100) (b).
This model has advantages compared with the existing entropy-based methods, including the availability of one control parameter (the number of network learning epochs), the fact that scaling the time series by amplitude does not affect the value of entropy, and the fact that it can be used for a series of any length. The method has a simple software implementation, and it is available for download to users in the form of an “NNetEn calculator 1.0.0.0” application [1].
The scientific novelty of the presented method is a new approach to estimating the entropy of time series using neural networks.
In https://doi.org/10.3390/a16050255 authors propose two new classification metrics: R2 Efficiency and Pearson Efficiency. The efficiency of NNetEn is verified on separation of two chaotic time series of sine mapping using dispersion analysis. For two close dynamic time series (r = 1.1918 and r = 1.2243), the F-ratio has reached the value of 124 and reflects high efficiency of the introduced method in classification problems. The electroencephalography signal classification for healthy persons and patients with Alzheimer disease illustrates the practical application of the NNetEn features. Authors computations demonstrate the synergistic effect of increasing classification accuracy when applying traditional entropy measures and the NNetEn concept conjointly. An implementation of the algorithms in Python is presented.
The program installation is done from PyPi repository using the following command (Listing 1).
Listing 1. Command to installation a NNetEn package.
pip install NNetEn
An instance of the NNetEn_entropy class is created by two commands (Listing 2).
Listing 2. Commands to create a NNetEn_entropy model.
from NNetEn import NNetEn_entropy
NNetEn = NNetEn_entropy(database = ‘D1’, mu = 1)
Arguments:
- database— (default = D1) Select dataset, D1—MNIST, D2—SARS-CoV-2-RBV1
- mu— (default = 1) usage fraction of the selected dataset μ (0.01, …, 1).
Output: The LogNNet neural network model is operated using normalized training and test sets contained in the NNetEn entropy class.
To call the calculation function, one command is used (Listing 3).
Listing 3. NNetEn calculation function with arguments.
value = NNetEn.calculation(time_series, epoch = 20, method = 3, metric = ’Acc’, log = False)
Arguments:
- time_series—input data with a time series in numpy array format.
- epoch— (default epoch = 20). The number of training epochs for the LogNNet neural network, with a number greater than 0.
- method— (default method = 3). One of 6 methods for forming a reservoir matrix from the time series M1, ..., M6.
- metric —(default metric = ‘Acc’). See Section 2.2 for neural network testing metrics. Options: metric = ‘Acc’, metric = ‘R2E’, metric = ‘PE’ (see Equation (6)).
- log— (default = False) Parameter for logging the main data used in the calculation. Recording is done in log.txt file
Output: NNetEn entropy value.
The source code of thePython package is stored on the site (https://github.com/izotov93/NNetEn (accessed on 26 April 2023)). Program code developed by Andrei Velichko and Yuriy Izotov.
References
- Andrei Velichko; Hanif Heidari; A Method for Estimating the Entropy of Time Series Using Artificial Neural Networks. Entropy 2021, 23, 1432, 10.3390/e23111432.
- Hamed Azami; Javier Escudero; Amplitude- and Fluctuation-Based Dispersion Entropy. Entropy 2018, 20, 210, 10.3390/e20030210.
- Bo Yan; Shaobo He; Kehui Sun; Design of a Network Permutation Entropy and Its Applications for Chaotic Time Series and EEG Signals. Entropy 2019, 21, 849, 10.3390/e21090849.
- Seif-Eddine Benkabou; Khalid Benabdeslem; Bruno Canitia; Unsupervised outlier detection for time series by entropy and dynamic time warping. Knowledge and Information Systems 2017, 54, 463-486, 10.1007/s10115-017-1067-8.
- Alejandro Ramirezrojas; Luciano Telesca; F Angulo-Brown; Entropy of geoelectrical time series in the natural time domain. Natural Hazards and Earth System Sciences 2011, 11, 219-225, 10.5194/nhess-11-219-2011.
- Yi Yin; Pengjian Shang; Weighted permutation entropy based on different symbolic approaches for financial time series. Physica A: Statistical Mechanics and its Applications 2016, 443, 137-148, 10.1016/j.physa.2015.09.067.
- Shannon Entropy . sciencedirect. Retrieved 2022-1-13
- Christophe Letellier; Estimating the Shannon Entropy: Recurrence Plots versus Symbolic Dynamics. Physical Review Letters 2006, 96, 254102, 10.1103/physrevlett.96.254102.
- David Cuesta–Frau; Permutation entropy: Influence of amplitude information on time series classification performance. Mathematical Biosciences and Engineering 2019, 16, 6842-6857, 10.3934/mbe.2019342.
- S. M. Pincus; Approximate entropy as a measure of system complexity.. Proceedings of the National Academy of Sciences 1991, 88, 2297-2301, 10.1073/pnas.88.6.2297.
- Joshua S. Richman; J. Randall Moorman; Physiological time-series analysis using approximate entropy and sample entropy. American Journal of Physiology-Heart and Circulatory Physiology 2000, 278, H2039-H2049, 10.1152/ajpheart.2000.278.6.h2039.
- Jongho Keum; Paulin Coulibaly; Sensitivity of Entropy Method to Time Series Length in Hydrometric Network Design. Journal of Hydrologic Engineering 2017, 22, 04017009, 10.1061/(asce)he.1943-5584.0001508.
- Luciano Zunino; Felipe Olivares; Felix Scholkmann; Osvaldo A. Rosso; Permutation entropy based time series analysis: Equalities in the input signal can lead to false conclusions. Physics Letters A 2017, 381, 1883-1892, 10.1016/j.physleta.2017.03.052.
- Stuart J. Watt; Antonio Politi; Permutation entropy revisited. Chaos, Solitons & Fractals 2019, 120, 95-99, 10.1016/j.chaos.2018.12.039.
- Yong Deng; Deng entropy. Chaos, Solitons & Fractals 2016, 91, 549-553, 10.1016/j.chaos.2016.07.014.
- Miguel Martínez-García; Yu Zhang; Kenji Suzuki; Yudong Zhang; Measuring System Entropy with a Deep Recurrent Neural Network Model. 2019 IEEE 17th International Conference on Industrial Informatics (INDIN) 2019, 1, 1253-1256, 10.1109/indin41052.2019.8972068.
- Andrei Velichko; Neural Network for Low-Memory IoT Devices and MNIST Image Recognition Using Kernels Based on Logistic Map. Electronics 2020, 9, 1432, 10.3390/electronics9091432.
