Your browser does not fully support modern features. Please upgrade for a smoother experience.
Please note this is a comparison between Version 1 by Imran Ashraf and Version 2 by Dean Liu.
Wind–solar hybrid systems combine solar photovoltaic cells and wind turbines to produce power from both solar and wind energy.
- artificial neural network
- energy prediction
- wind–solar prediction
1. Solar-Panel-Array Modeling
Solar panels interconnected to produce power is called a solar array. A software named hybrid optimization of multiple energy resources (HOMER) is an optimization tool which is used to design micropower systems. It basically optimizes the capacity of items using techno-economic analysis. In this software, a wide range of optimization can be performed in fields of solar energy systems, wind energy systems, hydro energy systems, and conventional generator systems, which can be modeled and optimized. The output of the photovoltaic cell in HOMER can be calculated using Equation (7).
where Pout is the output of array, Pr is the rated capability, f is the degradation factor as a percentage, GT is solar radiation incident to the array in W/m2W/m2, GT,ST shows solar radiation under standard conditions, αp is the temperature coefficient in %∘°C, TC is the panel temperature, and TC,ST indicates the panel temperature under standard conditions.
GT,ST is normally taken as 1 W/m2W/m2. The radiations in the first five months of the year 2022 are given in Figure 1.
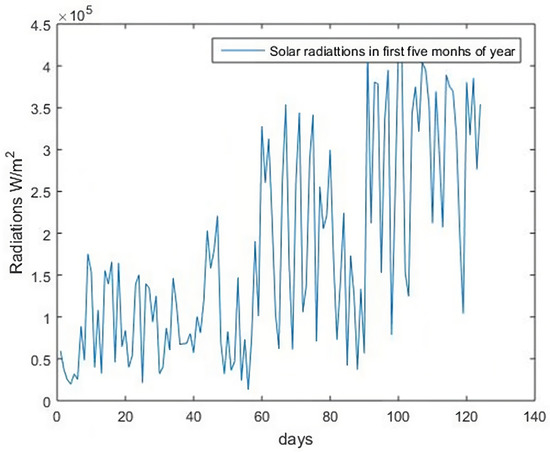 The efficiency of solar panels decreases with temperature and if no solar tracking system is used then the solar panels are held to a suitable inclination which is fixed. TIn this study, the suitable inclination angles for every month are discussed in Table 1. In addition, if there are alternating load types then converters can be used which convert AC into DC by a process called rectification.
The efficiency of solar panels decreases with temperature and if no solar tracking system is used then the solar panels are held to a suitable inclination which is fixed. TIn this study, the suitable inclination angles for every month are discussed in Table 1. In addition, if there are alternating load types then converters can be used which convert AC into DC by a process called rectification.

Figure 1. Solar radiations in January–May 2022.
Table 1. Optimum angle and solar irradiance for each month.
| Month | θ� | Monthly kW/m22 |
|---|---|---|
| January | 57 | 209.6 |
| February | 48 | 198 |
| March | 43 | 229.9 |
| April | 18 | 232 |
| May | 6 | 250.8 |
| June | 0 | 248 |
| July | 5 | 251 |
| August | 13 | 238 |
| September | 28 | 218.6 |
| October | 43 | 216 |
| November | 54 | 200 |
| December | 59 | 202 |
| Yearly radiation kW/m22 | 2694 | |
2. Solar Radiance
To find the optimal angle of inclination, the solar energy received on 1 m2m2 panel at different instances of the year at different angles (between 0∘°–90∘°) is derived with the help of simple integral calculations. The value of the optimum is given in Table 2. Using these angles, one can achieve maximum output from solar panels.3. Power Produced by Wind Turbines
To calculate wind speed, there are three steps. The first step is to find the wind speed approaching the turbine using a logarithmic law which is used to find the air speed at a hub height. Then, the generated output of the turbine is calculated through a comparison of the characteristic curve provided by the manufacturer, measured wind speed, and standard air density at a height equal to the hub height. Finally, the final output is adjusted for the actual air density. Wind speed at the corresponding hub height is calculated as:where Vℎ is the wind speed at the hub height in m, V is the wind speed in m/s, f is the degradation factor as a percentage, Hℎ is the hub height, H is the height of the wind-speed measurement point and α is the logarithmic law exponent.
The actual output of the wind turbine is calculated by adjusting actual air density conditions using
In the above Equation, ρ is the air density in kg/m33, ρST is the standard air density under standard atmospheric conditions, PST is the power produced by a wind turbine in kW under the standard conditions used by the turbine power curve, which is provided by manufacturers in Figure 2, below.
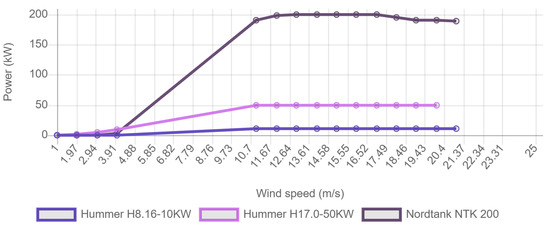 As mentioned previously, the ρST is the density of air in kg/m3kg/m3, its value is 1.225 kg/m3kg/m3 at standard conditions; A is the swept area of the wind-turbine blades in m2m2, which can be calculated by rotor diameter; and v is the upstream air speed in m/s. It is clear from the equation that wind power is cubic proportional to wind speed. The wind density measured at various locations is less diverse in nature as compared to wind speed. The wind-power capacity is proportional to the wind speed throughout the year [1][57]. Figure 2 provides a useful visualization of the relationship between the wind speed and power output of different turbines with a rated capacity of 10 kW, 50 kW, and 200 kW. The data required for this comparison was provided by [2][58]. The 11 m/s wind speed is required for rated outputs 10, 50, and 200 kW wind turbines and produces almost little to no power during 0–4 m/s wind speeds. Turbines are bound and are not allowed to produce power higher than that for which they are designed to avoid failures and this is achieved by adjusting blade angles. From this, it is apparent that the installation of wind turbines should only be carried out at locations with a minimum wind speed of 4 m/s, and a maximum of nearly 21 m/s, while the average should be around 11 m/s. However, these values can change depending on the design of the wind turbines. Furthermore, safety mechanisms in the case of high wind speed are necessary as well. Our model can help in the prediction of such high wind speeds.
As mentioned previously, the ρST is the density of air in kg/m3kg/m3, its value is 1.225 kg/m3kg/m3 at standard conditions; A is the swept area of the wind-turbine blades in m2m2, which can be calculated by rotor diameter; and v is the upstream air speed in m/s. It is clear from the equation that wind power is cubic proportional to wind speed. The wind density measured at various locations is less diverse in nature as compared to wind speed. The wind-power capacity is proportional to the wind speed throughout the year [1][57]. Figure 2 provides a useful visualization of the relationship between the wind speed and power output of different turbines with a rated capacity of 10 kW, 50 kW, and 200 kW. The data required for this comparison was provided by [2][58]. The 11 m/s wind speed is required for rated outputs 10, 50, and 200 kW wind turbines and produces almost little to no power during 0–4 m/s wind speeds. Turbines are bound and are not allowed to produce power higher than that for which they are designed to avoid failures and this is achieved by adjusting blade angles. From this, it is apparent that the installation of wind turbines should only be carried out at locations with a minimum wind speed of 4 m/s, and a maximum of nearly 21 m/s, while the average should be around 11 m/s. However, these values can change depending on the design of the wind turbines. Furthermore, safety mechanisms in the case of high wind speed are necessary as well. Our model can help in the prediction of such high wind speeds.

Figure 2. Power vs wind speed curve for different rated wind turbines.
