Magnetic Materials for Electrical Machines

Version	Summary	Created by	Modification	Content Size	Created at	Operation
1		Thang Pham	+ 1776 word(s)	1776	2021-01-27 05:13:16	\|
2	format correct	Catherine Yang	-1 word(s)	1775	2021-02-25 10:57:39	\|

This entry is adapted from the peer-reviewed paper 10.3390/en14020283

Additive manufacturing has many advantages over traditional manufacturing methods and has been increasingly used in medical, aerospace, and automotive applications. The flexibility of additive manufacturing technologies to fabricate complex geometries from copper, polymer, and ferrous materials presents unique opportunities for new design concepts and improved machine power density without significantly increasing production and prototyping cost. Topology optimization investigates the optimal distribution of single or multiple materials within a defined design space, and can lead to unique geometries not realizable with conventional optimization techniques. As an enabling technology, additive manufacturing provides an opportunity for machine designers to overcome the current manufacturing limitation that inhibit adoption of topology optimization. Successful integration of additive manufacturing and topology optimization for fabricating magnetic components for electrical machines can enable new tools for electrical machine designers. This article presents a comprehensive review of the latest achievements in the application of additive manufacturing, topology optimization, and their integration for electrical machines and their magnetic components.

topology optimization magnetic materials

1. Introduction

The electrical machine is considered a key part in electric drives, which account for approximately 50% to 70% of electricity usage in the EU and the United States ^[1]. Its applications include, but are not limited to, compressors, HVAC systems, power tools, generators, electric and hybrid vehicles, elevators, and MAGLEV trains. In the last decade, there have been consistent efforts from both the US Department of Energy and the EU to advance the design and development of future generations of electrical machines that positively impact the environment and reduce greenhouse gas emissions ^[1]^[2]. The next generation electrical machines include designs with high efficiency and power density; however, another important aspect is their environmentally friendly construction, including aspects such as minimal material waste and recyclability.

2. Topology Optimization for Magnetic Structures

The shaping of the magnetic structures for electrical machines can be generally categorized into two groups: (1) conventional shaping and optimization techniques, and (2) topology optimization. For the conventional shaping techniques, mathematical models and sensitivity analysis are typically used on a pre-selected machine geometry template ^[3]^[4]. The computational and analytical efforts are often intensive to improve the accuracy of the calculation of the airgap flux density, torque components, and the magnetic flux density distribution ^[5]. Conventional optimization, which is typically based on evolutionary multi-objective optimization algorithms, further refines the shape of the magnetic structures to improve the machine performance. As a result, the derivation of uniquely shaped magnetic structures for electrical machines can be slow.

Emerging from structural optimization, TO is increasingly applied in magnetic devices ^[6], and subsequently in design of electrical machines, especially at the component level such as magnetic cores ^[7] and permanent magnets ^[8]. In contrast to conventional optimization, TO can generate an initial geometry template from scratch with less analytical modeling ^[9]. In general, TO investigates optimal distribution of single or multiple materials within a defined design space ^[10]. Compared to conventional optimization shaping techniques, it offers additional flexibility in optimizing the geometry of the magnetic components for attaining the desired performance. Thus, TO can yield unique shapes that are generally not realizable with conventional optimization approach.

2.1. Topology Optimization Shaping Techniques

In seeking unique and optimal geometry either made of single or multiple materials, TO can employ approaches such as the on/off method and the density-based method. For the on/off method, the design space is typically divided into cells or put into a grid-like structure. Each cell is then represented by a variable, such as normalized density $ρ_{n}$ , which can be assigned a value of zero or one, as illustrated in Figure 1a. Zero and one indicate the absence and presence of material, respectively. The pattern of the material distribution can be determined via selection of objective functions and use of evolutionary multi-objective or gradient-based algorithm. Thus, in a finalized topology optimized design via on/off method, it typically has an unconventional geometry.

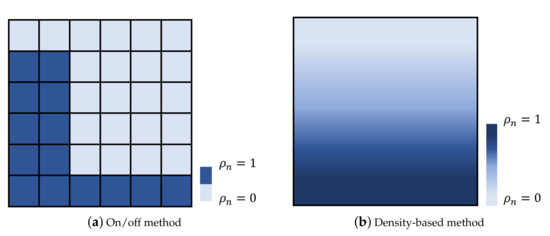
Figure 1. Illustrations of two topology optimization methods for magnetic cores. Here, $ρ_{n}$ is the normalized density variable under optimization.

An on/off TO is modified to optimally distribute the soft magnetic material for a rotor core of an interior permanent magnet machine and then to smooth the shape of the design is presented as shown in Figure 2. Here, the TO algorithm in ^[11] first uses a genetic-based method to find an optimal solution in the global search space. The solution is then smoothed out via the use of a gradient-based method in the local search space. The illustration of the modified algorithm is shown in Figure 3.

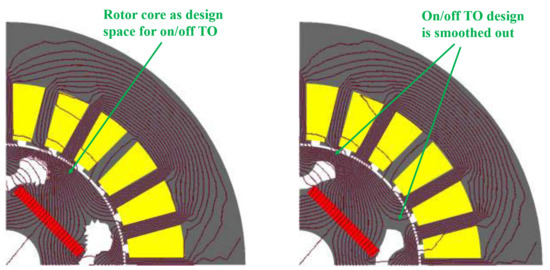
Figure 2. Example of a rotor core of a permanent magnet machine achieved via on/off TO algorithm. The TO design is smoothed out. Figure is adapted from [8].

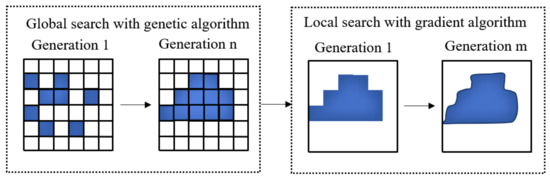
Figure 3. Example of an on/off TO algorithm where a genetic-based algorithm is combined with a gradient-based algorithm. The shape achieved with this algorithm is smoother. Figure is adapted from ^[11].

The on/off TO method can also be applied to find the optimal distribution of multiple materials such as iron, copper, and permanent magnet. In ^[12], a multi-material on/off TO algorithm is used to maximize the force acted on the plunger of a permanent magnet linear actuator. The TO optimal design achieves a unique structure compared to the original design and an additional increase of 40% in average force, as shown in Figure 4.

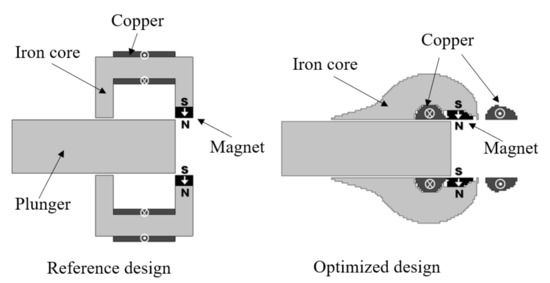
Figure 4. Illustration on the result of the on/off TO algorithm for multiple materials on a permanent magnet linear actuator. Figure is adapted from ^[12].

As the on/off method assigns the optimizing density variable to be binary, the density-based method assigns the density variable $ρ_{n}$

a continuous value between zero and one, as illustrated in Figure 1b. A version of the density-based method is applied on a rotor core of a permanent magnet synchronous machine in ^[13]. Here, the exclusive magnetic-based topology optimization works toward maximizing the average torque while constraining the torque ripple and cogging, and finally leads to the unique design of the rotor core as shown in Figure 5. The white areas in the rotor core represent the permanent magnet, while the dark red areas and the dark blue areas represent iron and air, respectively. In between them are regions with intermediate density values, which are represented with different shades of colors.

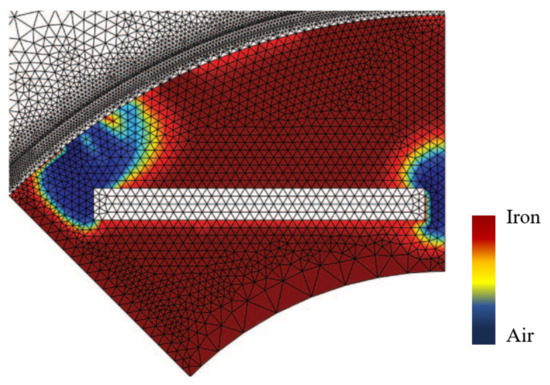
Energies 14 00283 g013 550

Figure 5. Illustration of density-based topology optimization for the rotor core of an interior permanent magnet synchronous machine, adapted from ^[13].

Magnetic-based topology optimization may result in unique designs that achieve desired electromagnetic performance. These unique designs also present challenges that must be considered. Exclusively using magnetic-based TO algorithm results in designs that are only optimized for electromagnetic performance. Since mechanical stress of the structure is not included as an objective, the mechanical integrity of the magnetic-based TO design may become a concern. A magnetic-based TO design with a unique distribution of air pockets is shown in Figure 6. Here the TO algorithm, however, does not include mechanical stress analysis in the iron regions adjacent to the air pockets. This can lead to durability performance of the design under real operating condition where the adjacent iron regions can be subjected to stress values between 240MPa to above 450MPa ^[14]. Coupled structural and electromagnetic analysis can provide tradeoff solutions to address this concern. In ^[15], the density-based method is applied on rotors of wound field synchronous machines. The optimized rotors are achieved via the integration of both magnetic and structural topology optimization analysis.

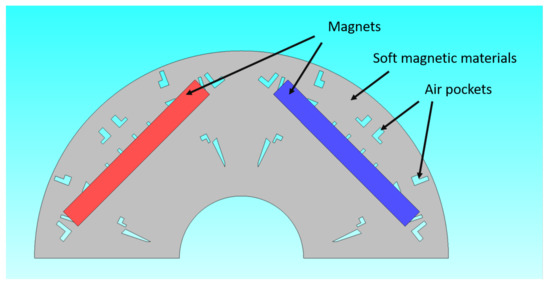
Energies 14 00283 g014 550

Figure 6. Example of magnetic-based topology optimization for the rotor core of an interior permanent magnet synchronous machine, adapted from ^[16]. Iron regions adjacent to air pockets and magnets can be subjected to high mechanical stress.

2.2. A Design Tool for Additive Manufacturing

As TO is increasingly adopted in developing unique geometries for electrical machines, manufacturability of the unique magnetic core designs is equally important. Design complexities may increase manufacturing cost for electrical steel laminations. Additionally, manufacturing methods including subtractive techniques can compromise the magnetic properties of punched laminations ^[17], leading to magnetic cores with inferior magnetic performance compared the mother coil. Thus, topology optimized designs in Figure 2 and Figure 6 may not be able to achieve the desired magnetic performance. Powder metallurgy can potentially be used as an alternative approach to fabricate such complex designs, as shown in Figure 7. However, the added cost of molding and tooling may become a concern.

Energies 14 00283 g015 550

Figure 7. An example on topology optimization of a rotor core for a switched reluctance motor ^[18].

In application where non-homogeneous magnetic core is desired as in ^[19]^[20], powder metallurgy manufacturing approach is not a viable solution for production as it may reach the limits in fabricating such composite, non-homogenous structures. Similarly, designs of magnetic cores for electrical machines generated with the TO density-based method as in ^[13]^[15], may request material whose properties may not correspond to an available material ^[21]. Additive manufacturing can potentially overcome difficulties typically observed in conventional manufacturing methods, and in some cases is the only viable manufacturing solution ^[22].

Recent advancements in AM as well as the proliferation of its application in fabricating magnetic components for electrical machine have revitalized TO as an advanced design tool. The synergy between TO and AM can potentially lead to the development of magnetic components, whose properties and geometries are complex. Investigations in integration of TO toward AM in producing magnetic components for electrical machines have shown very promising results. In ^[23], a topology optimized design of a rotor core of a surface mount permanent magnet machine is additively manufactured via the SLM process, as shown in Figure 8. Here, the TO algorithm combines both the electromagnetic and structural optimization stages to achieve a rotor core geometry with 50% reduction in weight, at a tradeoff of less than 2% in average torque, while achieving maximum von Mises stress in the optimized rotor core well within the yield strength of the material. The result of this work highlights the exploitation of multi-physics TO as an advanced design tool for AM in developing new, unconventional electrical machines.

Figure 8. Optimized rotor core via coupled magnetic-structural TO. The design is then additively manufactured via SLM. Figure is modified from ^[23].

The integration of TO into AM is also seen in fabricating permanent magnet with unique shapes and structures. In ^[8], TO is implemented to generate the design of a permanent magnet such that it can provide magnetic flux density waveform close to the predefined external field. The design is then additively manufactured via the FDM process from a magnetic compound of NdFeB powder, ferrites, and polymers, Figure 9. In ^[24], permanent magnet made of multiple magnet grades is proposed for a surface mounted machine to reduce manufacturing cost without penalizing machine performance. The multi-grade magnet is optimized, and investigated via finite element analysis. Although TO is not implemented, the analysis suggests the combined use of TO and AM technologies in potentially producing lower cost magnets.

Figure 9. Topology optimized magnet. The design is then additively manufactured via fused deposition modeling. Figure is modified from ^[8].

References

Commission Regulation (EU) 2019/1781. Available online: https://op.europa.eu/en/publication-detail/-/publication/218c6599-f734-11e9-8c1f-01aa75ed71a1/language-en (accessed on 1 October 2019).
Energy Department Awards $22 Million to Support Next Generation Electric Machines for Manufacturing. Available online: https://www.energy.gov/articles/energy-department-awards-22-million-support-next-generation-electric-machines-manufacturing (accessed on 16 September 2015).
Kano, Y.; Terahai, T.; Kosaka, T.; Matsui, N.; Nakanishi, T. A new flux-barrier design of torque ripple reduction in saliency-based sensorless drive IPM motors for general industrial applications. In Proceedings of the 2009 IEEE Energy Conversion Congress and Exposition, San Jose, CA, USA, 20–24 September 2009; pp. 1939–1945.
Fei, W.; Luk, P.C.K.; Shen, J.X.; Xia, B.; Wang, Y. Permanent-Magnet Flux-Switching Integrated Starter Generator With Different Rotor Configurations for Cogging Torque and Torque Ripple Mitigations. IEEE Trans. Ind. Appl. 2011, 47, 1247–1256.
Valavi, M.; Nysveen, A.; Nilssen, R. Characterization of radial magnetic forces in low-speed permanent magnet wind generator with non-overlapping concentrated windings. In Proceedings of the 2012 XXth International Conference on Electrical Machines, Marseille, France, 2–5 September 2012; pp. 2943–2948.
Dyck, D.N.; Lowther, D.A. Automated design of magnetic devices by optimizing material distribution. IEEE Trans. Magn. 1996, 32, 1188–1193.
Okamoto, Y.; Hoshino, R.; Wakao, S.; Tsuburaya, T. Improvement of Torque Characteristics For a Synchronous Reluctance Motor Using MMA-based Topology Optimization Method. IEEE Trans. Magn. 2018, 54, 1–4.
Huber, C.; Abert, C.; Bruckner, F.; Pfaff, C.; Kriwet, J.; Groenefeld, M.; Teliban, I.; Vogler, C.; Suess, D. Topology optimized and 3D printed polymer-bonded permanent magnets for a predefined external field. J. Appl. Phys. 2017, 122, 053904.
Wang, S.; Kang, J. Topology optimization of nonlinear magnetostatics. IEEE Trans. Magn. 2002, 38, 1029–1032.
Bendsoe, M.; Sigmund, O. Topology Optimization: Theory, Methods, and Applications; Engineering Online Library; Springer: Berlin/Heidelberg, Germany, 2003.
Hidaka, Y.; Sato, T.; Igarashi, H. Topology Optimization Method Based on On–Off Method and Level Set Approach. IEEE Trans. Magn. 2014, 50, 617–620.
Lee, J.; Dede, E.M.; Nomura, T. Simultaneous Design Optimization of Permanent Magnet, Coils, and Ferromagnetic Material in Actuators. IEEE Trans. Magn. 2011, 47, 4712–4716.
Hermann, A.N.A.; Mijatovic, N.; Henriksen, M.L. Topology optimisation of PMSM rotor for pump application. In Proceedings of the 2016 XXII International Conference on Electrical Machines (ICEM), Lausanne, Switzerland, 4–7 September 2016; pp. 2119–2125.
Jung, J.; Lee, B.; Kim, D.; Hong, J.; Kim, J.; Jeon, S.; Song, D. Mechanical Stress Reduction of Rotor Core of Interior Permanent Magnet Synchronous Motor. IEEE Trans. Magn. 2012, 48, 911–914.
Guo, F.; Salameh, M.; Krishnamurthy, M.; Brown, I.P. Multimaterial Magneto-Structural Topology Optimization of Wound Field Synchronous Machine Rotors. IEEE Trans. Ind. Appl. 2020, 56, 3656–3667.
Jung, S.; Ro, J.; Jung, H. A Hybrid Algorithm Using Shape and Topology Optimization for the Design of Electric Machines. IEEE Trans. Magn. 2018, 54, 1–4.
Bali, M. Magnetic Material Degradation Due to Different Cutting Techniques and its Modeling for Electric Machine Design. Ph.D. Thesis, Technischen Universitat Graz, Graz, Austria, 2016.
Lee, J. Structural Design Optimization of Electric Motors to Improve Torque Performance. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2010.
Yan, Y.; Liu, L.; Ding, C.; Nguyen, L.; Moss, J.; Mei, Y.; Lu, G. Additive Manufacturing of Magnetic Components for Heterogeneous Integration. In Proceedings of the 2017 IEEE 67th Electronic Components and Technology Conference (ECTC), Orlando, FL, USA, 30 March–2 June 2017; pp. 324–330.
Pham, T.Q.; Foster, S.N. Additive Manufacturing of Non-homogeneous Magnetic Cores for Electrical Machines Opportunities and Challenges. In Proceedings of the 2020 International Conference on Electrical Machines (ICEM), Gothenburg, Sweden, 23–26 August 2020; Volume 1, pp. 1623–1629.
Dyck, D.N.; Lowther, D.A. Composite microstructure of permeable material for the optimized material distribution method of automated design. IEEE Trans. Magn. 1997, 33, 1828–1831.
Liu, L.; Ding, C.; Lu, S.; Ge, T.; Yan, Y.; Mei, Y.; Ngo, K.D.T.; Lu, G. Design and Additive Manufacturing of Multipermeability Magnetic Cores. IEEE Trans. Ind. Appl. 2018, 54, 3541–3547.
Garibaldi, M.; Gerada, C.; Ashcroft, I.; Hague, R. Free-Form Design of Electrical Machine Rotor Cores for Production Using Additive Manufacturing. J. Mech. Des. 2019, 141, 071401.
McGarry, C.; McDonald, A.; Alotaibi, N. Optimisation of Additively Manufactured Permanent Magnets for Wind Turbine Generators. In Proceedings of the 2019 IEEE International Electric Machines Drives Conference (IEMDC), San Deigo, CA, USA, 12–15 May 2019; pp. 656–663.

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.

Upload a video for this entry

Information

Subjects: Others

Contributor MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :

Thang Pham

View Times: 1.1K

Update Date: 25 Feb 2021

Table of Contents

Video Upload Options

Confirm