| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Alexandros El Sachat | + 5488 word(s) | 5488 | 2021-01-25 04:59:20 | | | |
| 2 | Bruce Ren | -24 word(s) | 5464 | 2021-02-02 03:26:42 | | |
Video Upload Options
Heat dissipation and thermal management are central challenges in various areas of science and technology and are critical issues for the majority of nanoelectronic devices. In this review, we focus on experimental advances in thermal characterization and phonon engineering that have drastically increased the understanding of heat transport and demonstrated efficient ways to control heat propagation in nanomaterials.
1. Introduction
Advances in the electronics industry have led to an increased need for novel approaches to thermal management to improve devices performance and reliability, by controlling the dissipation of the energy generated in the devices. In particular, the possibility of controlling heat propagation by engineering the phononic properties of the fundamental components is of great interest in nanoelectronics—where heat dissipation will play a major role in determining the performance of high-density nanoscale circuits —or in thermoelectric materials—where materials with low thermal conductivities are desired. The main heat carriers in these materials are phonons, thus understanding and controlling phonon transport are issues highly connected with the successful development of low-power electronics and efficient thermoelectric energy harvesting.
However, with the continuous miniaturization of electronic devices reaching physical limits, heat transport and thermal management are becoming increasingly more challenging. For instance, the characteristic dimensions of electronic components have become comparable to the phonon mean free path (MFP), which inevitably increases the power density and complicates heat removal [1][2]. In addition, the large density of interfaces, contacts, and boundaries that appear at extremely small length scales in today’s electronics indicates the importance of further optimizing nanoscale thermal characterization tools. Advances in measurement techniques together with theoretical efforts have enabled a better understanding of novel heat transport mechanisms, e.g., hydrodynamic phonon transport, coherent and ballistic transport, thermal localization, and finally phonon propagation at the nanoscale, opening exciting prospects for thermal investigations of materials even at the atomic level [3][4]. In parallel, progress in material growth and nanofabrication have enabled remarkable advances in thermal transport engineering. The concept of phonon engineering has been employed in various nanomaterials during recent decades, showing its potential in thermal management.
2. Engineering the Phonon Thermal Conduction in Semiconductor Nanostructures and 2D Materials
In semiconductor and insulators, the dominant carriers of heat conduction are lattices waves or phonons. A phonon is a quasi-particle which represents quantized modes of the vibrational energy of an atom or group of atoms in a lattice. Considering that phonons are pseudo-particles, it is possible to associate energy ħω (where ħ is the reduced Planck’s constant ħ = h/(2π) and ω is the angular frequency) and a pseudo-momentum p = ħq (where q is the wavevector), which obey Bose–Einstein statistics [5][6]. The wavelength dependence of the phonon energy can be represented as a dispersion relation, i.e., a relationship between the phonon frequency and its wavevector. The slope of a dispersion relation curve determines the phonon group velocity.
The ability to transport heat is denominated thermal conductivity. It plays a fundamental role in the design and performance of the technological devices. The calculation of the thermal conductivity (k) in semiconductor material requires the knowledge of three major frequency-dependent parameters, namely, specific heat (CV), phonon group velocity (vg), and phonon mean free path (Λ). Finally, the expression for thermal conductivity from the kinetic theory of gases is given by: k = CV·vg·Λ.
A major limitation to determine k is the knowledge of mean free path Λ = vg/τ, where τ is the effective or total phonon lifetime. In general, τ is estimated using the Matthiessen’s rule assuming that each scattering mechanism is independent of each other. The phonon lifetime is mainly limited by: phonon-phonon scattering (τpp), impurity scattering (τI) and boundary scattering (τB). The latter is pronounced in low-dimensional materials due to the dimensionality confinement, which results in modified heat transport properties. The possibility of tuning the thermal conductivity of low-dimensional materials via phonon engineering is of high importance and might lead in multiple breakthroughs (e.g., high figure of merit, improved energy efficiency).
2.1. Semiconductor Nanostructures
Modifications of the dispersion relation have a direct impact on the acoustic phonon properties of nanostructures, such as phonon group velocity [7], polarization and density of states. These can usually be induced either through boundary conditions in the individual nanostructures, e.g., free-standing nanowires (NWs) or thin films, or via periodic boundary conditions, e.g., superlattices (SLs) and phononic crystals (PnCs). In principle, heat transport in such nanostructures decreases either due to classical size effects or phonon confinement effects. The first is related to increased phonon-boundary scattering and is pronounced when the characteristic dimensions of the nanostructures are comparable to the phonon MFP [8]. When nanostructures dimensions are in the order of or smaller than the phonon wavelength, phonon confinement or coherent effects appear, modifying dispersion branches, which in turn modifies the group velocity, phonon density of states, and phonon lifetime [9][10][11]. At room temperature, the impact of phonon confinement on the thermal transport is almost negligible. Instead, the decrease of the thermal conductivity is mainly attributed to diffuse scattering of phonons at the boundaries. Although this mechanism has been widely explored and exploited, several works propose the use of the phonon confinement effect as a mean to control the heat flow [12][13].
The real impact of the phonon confinement on thermal transport at room temperature has only been observed using superlattices [14][15]. However, in most cases nanofabrication processes result in nanostructures with length scales larger than the phonon wavelength of the dominant heat carriers (at room temperature <5 nm) and limits the observation of confinement effects. Cryogenic temperatures (T < 10 K) can overcome this problem [16][17]. In the next sections we present recent experimental works that have demonstrated efficient heat transport control in semiconductor nanostructures.
2.1.1. Membrane-Based Structures
In membrane-based structures, the reduction of in-plane thermal conductivity (k) due to phonon-boundary scattering has been clearly demonstrated in thermal transport experiments in silicon layers of different thickness, performed over a large range of temperatures [18][19][20][21]. The results from these studies showed that the thermal conductivity of Si can be effectively tuned by decreasing its thickness. In parallel, experimental works have demonstrated that the fabrication of Si thin films with two-dimensional periodic patterning, i.e., phononic crystals (PnCs), is an efficient way to modify the phonon spectrum, control heat conduction and improve the thermoelectric efficiency [22][23].
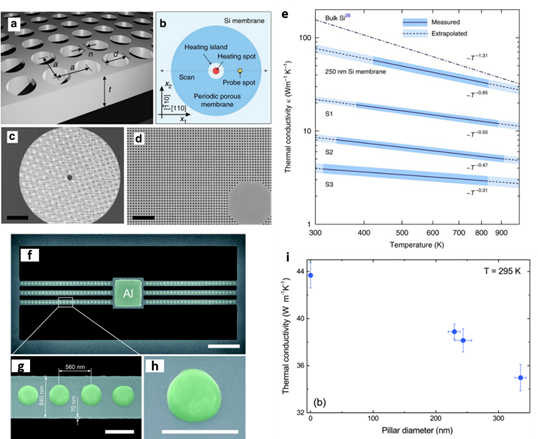
Recent thermal transport studies have shown that the in-plane thermal conductivity of silicon and its temperature dependence can be effectively reduced and tuned by patterning periodic arrays of holes [24][25][26] or arrays of pillars [27][28][29]. In silicon membranes with patterned arrays of holes (see Figure 1a–d) a strong reduction of ~90% of the thermal conductivity was found compared to unpatterned Si membranes of equal thickness. Figure 1e displays the thermal conductivity of PnCs with different filling fraction. At room temperature the reduction of the thermal conductivity was attributed mainly to the shortening of the phonon mean free path due to diffuse (incoherent) phonon-boundary scattering. Although the increase of the surface-to-volume ratio leads to increased boundary scattering, at higher temperatures the phonon–phonon scattering dominates over the boundary scattering. This is observed through the smaller relative reduction in k, compared to room temperature. The impact of coherent phonon scattering was found to be significant in the thermal conductivity reduction of similar structures only at low temperatures, where thermal phonon wavelengths become longer and comparable with the period of the holes [30][31][32].
Figure 1. Phonon engineering in membrane-based structures. (a) Schematic of a hole-based PnC—square lattice of cylindrical holes in a 250 nm thick suspended membrane, where d is the hole diameter, a is the lattice parameter, and n is the neck size. (b) Schematic of a sample design showing relative laser heating and probing positions and (c,d) scanning electron microscope images of a PnC with a = 250 nm and d = 140 nm. Scale bars in (c,d) are 20 and 2 μm, respectively. (e) Thermal conductivity of hole-based PnCs as a function of temperature and filling fraction S with S1 = 0.159, S2 = 0.246 and S3 = 0.332. (f,g) SEM images of a pillar-based PnC—Si nanobeam with one-dimensional arrays of pillars with a period of 560 nm and pillar base diameters of 229.5, 243.5 and 335 nm and (h) SEM image of a single nanopillar. Scale bars are (f) 5 µm and (g–h) 500 nm. (i) Thermal conductivity of different nanobeams as a function of pillar diameter at 295 K. (a–e) reproduced with permission from [24]. Copyright Springer Nature, 2017. (f–i) Reproduced with permission from [28], Copyright Royal Society of Chemistry, 2017.
In pillar-based PnCs the reduction of the thermal conductivity was weaker in comparison with the hole-based PnCs while coherent effects were found to be insignificant even at low temperatures. This was observed for pillar-based PnCs fabricated by patterning Al nanopillars of different diameters on suspended Si nanobeams [28]. Figure 1f–h shows the geometry of the investigated Si nanobeam with one-dimensional arrays of pillars with a period of 560 nm and various pillar diameters. The thermal conductivity of these structures at room temperature was observed to decrease with increasing diameter, with a maximum thermal conductivity reduction of approximately 20% (see Figure 1e). The authors attributed this behavior to the increased phonon scattering at the pillar/beam interface due to the intermixing of aluminum and silicon atoms. The same group later fabricated nanopillars on suspended silicon membranes and investigated the impact of nanopillars on the thermal conductivity at low temperatures (4−300 K) [29]. They found the thermal conductivity reduction caused by the nanopillars to be approximately ~16%, which was attributed mainly to incoherent phonon boundary scattering. It is interesting to note that although the rate of the thermal conductivity reduction in these structures was much lower than the hole-based PnCs, the electrical conduction remained unaffected, or even increased, since no volume removal was required.
Other phononic structures have been fabricated by introducing short-range positional disorder in PnCs, which showed similar values of the thermal conductivity at room temperature compared with the fully periodic structures [33]. Although the phonon spectrum in the GHz range may be modified, these works evidenced that at room temperature, thermal transport is mainly diffusive (particle-like) and dominated by phonons in the THz range.
Since phonons are intrinsically waves, the control over their coherence can open fundamentally new routes for manipulating the heat flow. Venkatasubramanian was one of the first who discussed about coherent effects on thermal measurements in superlattices (SLs). He presented a physical model to understand the reduction of the k based on the coherent backscattering of phonon waves at the superlattice interfaces [34]. Since then, the coherent concept was adopted by several authors to explain thermal conduction processes in superlattices and phononic crystals [35]. However, the interpretation of coherent thermal transport is still under debate and the experimental reports still remain inconclusive [36]. Some experimental reports that claimed coherent effects [37][38][39] have been contrasted by numerical simulations [40][41]. Concluding that some of these claims could be explained by particle-based models without considering coherent phonon transport [42].
Part of these controversies comes from the nature of the coherent transport in the context of thermal transport which is not well understood. In general, coherence involves a measurable phase-dependence between waves over a given time interval, e.g., the interaction of monochromatic waves. However, this notion cannot be applied directly in case of heat conduction, which involves all the thermally excited phonons in a structure. Latour et al. tackled this problem by treating the phonon-coherence length in terms of correlation functions in superlattices [43]. The discussion about coherent effect in superlattices will be given.
The sample quality is also another important parameter to take into account to observe coherent effects. The structures have to have periodicities in the order of the wavelength of the dominant thermal phonons (few nm) with atomically smooth surfaces (or interfaces) to avoid diffusive scattering of the heat carriers. For the case of silicon, the dominant phonon wavelength at room temperature is 1–2 nm [41]. On the other hand, the present state of the art in nanofabrication can produce patterned structures with dimensions down to several tens of nanometers with block-copolymer technologies and hundreds of nanometers via a top-down approach [42]. Such dimensions can tailor the dispersion relations of phonons in the GHz range with a poor contribution to the thermal properties at room temperature. Lee et al. demonstrate that phonon coherence is negligible in the thermal transport of silicon nanomeshes with periodicities ≥100 nm and T > 14 K. Xiao et al. also found a negligible contribution of wave effects in the total thermal resistance of Si thin film with increased rows of nanopores with temperatures ranging from 85–300 K [44].
On the other hand, at lower temperatures, Zen et al., demonstrated the impact of the coherent effect in the thermal transport in patterned silicon nitride membranes in the sub-Kelvin regime. They showed the direct correlation between the thermal conductance, calculated from the modified phonon dispersion relation, and experimental measurements. Maire et al. measured the reduction in the k in a patterned Si phononic crystal at 4 K. They claimed that the presence of phonon interference is the origin of the reduction in k of a phononic crystal with an ordered array of holes as compared to the thermal conductivity of structures with randomly positioned holes.
2.1.2. Nanowires
Tuning phonon properties and heat conduction via phonon engineering has been demonstrated in NWs consisting of different materials, shapes, geometries and composition. The influence of diameter of NWs on the phonon thermal conductivity at room temperature has been thoroughly investigated in previous studies [45][46][47][48]. In these experiments, classical size effects were dominant and the thermal conductivity of the NWs was found to be suppressed by almost two orders of magnitude compared to their bulk counterparts, mainly due to the increased phonon boundary scattering. The dependence of the thermal conductivity on diameter is still valid at high temperatures as has been recently demonstrated by Lee et al. [48]. Additionally, in this work the authors showed an increasing contribution of high-frequency phonons as the temperature increases and the NW diameter decreases.
Furthermore, recent works have experimentally demonstrated ballistic heat conduction in Si, SiGe, and GaN NWs of different lengths at room temperature [49][50]. The length-dependent thermal conductivity measured in these studies showed that ballistic heat conduction can be preserved at room temperature for several micrometer length wires. For instance, Vakulov et al. [50] showed that in 25 nm diameter GaN NWs a room-temperature ballistic heat flow persist at least 15 μm. Such evidence showed the great potential of semiconductor NWs to be used for improved thermal management in applications such as phonon transistors [51][52] and computer chips, where rapid heat removal is required.
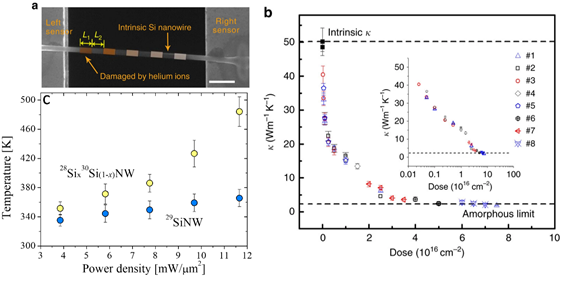
In parallel, different methods to further modulate the thermal conductivity of NWs have been proposed such as the fabrication of core-shell NWs. For example, a strong thermal conductivity reduction was found in Si and SiGe alloy NWs with diameters of few tens of nanometers, indicating the important effect of the core–shell interface on phonon transport [53]. Juntunen et al. also found up to ∼60% reduction of the thermal conductivity of GaAs NWs coated with AlAs shells [54]. A different study showed that the k along a single Si nanowire can be tuned (between crystalline and amorphous limits) through selective helium ion irradiation with a well-controlled dose [55]. Figure 2a displays a SEM image of a single Si nanowire, which was irradiated at different positions with well-controlled helium ion doses. Figure 2b shows the reduction in k as a function of the helium ion doses, where a clear transition from crystalline Si to amorphous phase can be observed at a dose between 1.5 × 1016 and 2.5 × 1016 cm−2.
Figure 2. Phonon engineering in nanowires. (a) SEM image of a Si NW damaged by helium ions (sample #1). The portions colored orange denote the parts damaged by helium ions; the uncolored portions denote the intrinsic Si NW. Scale bar, 1 mm. (b) Measured k of samples #1–#8 versus dose. Inset: the same data plotted on a logarithmic scale. The solid black square denotes the k of intrinsic NWs (namely, with zero dose). (c) Plot of the measured power density as a function of the laser heating for different isotopically engineered Si NWs. (a, b) Reproduced with permission from [55]. Copyright Springer Nature, 2017. (c) Adapted from Mukjerjee et al. [56].
More recent experimental studies demonstrated that manipulation of crystal phase, isotope composition and mass disorder are effective ways to control heat transport in silicon NWs. For instance, Mukherjee et al. showed that isotopically mixed metal-catalyzed 28Six30Si1−x NWs exhibit enhanced phonon scattering and approximately 30% decreased thermal conductivity induced by mass disorder in comparison with isotopically pure 29Si NWs [56]. Figure 2c shows the measured power density as a function of the laser heating for the two types of NWs, which was used together with a model to extract the local temperature and thermal conductivity of the NWs. The same authors later found that the thermal conductivity of Si NWs with tailor-made isotopic compositions can be reduced by up to ∼40% relative to that of isotopically pure NWs [57]. The lowest k value was found for a rhombohedral phase in isotopically mixed 28Six 30Si1-x nanowires with composition close to the highest mass disorder. Similarly, the authors used the same methodology to extract the thermal conductivity of the NWs.
2.1.3. Superlattices
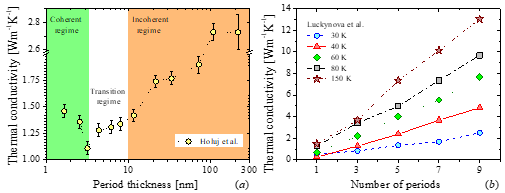
The first attempts to manipulate the wave nature of phonons were carried out by using alternating thin layers of dissimilar materials to realize a super periodicity of atomic position, i.e., a superlattice (SL). Due to the possibility to modify the dispersion relation as well as to create miniband and minigaps, stop bands and acoustic mirrors, the thermal transport community envisioned a very large potential to control the heat propagation with SLs [58]. The thermal transport in nanoscale SLs shows a crossover between coherent and incoherent phonon transport along the layered axis. The transition depends on the period thickness (dSL = d1 + d2, where d1 and d2 are the thickness of each layer) and the coherent length of the phonons. The crossover occurs when the interface density, 1/ dSL, is large enough to limit the propagation of high frequency phonons (particle-like) so that the thermal transport is governed by low frequency phonons (wave-like). The transition between coherent-incoherent (wave-particle) transport is observed as a minimum in the k as a function of dSL as is shown in Figure 3a. Although this behavior was predicted in 2000 , this observation has been hidden probably by the low quality of the interfaces, which destroys the otherwise perfect periodic system, disallowing coherent phonon transport. Recently, Ravichandran et al. presented the first unambiguous experimental demonstration of this crossover using epitaxial perovskite-based SLs. Luckyanova et al. presented another fingerprint of coherent thermal transport, namely, a linear dependence of k with respect to the number periods N (see Figure 3b). This behavior arises when, in the coherent regime, the phonon mean free paths are equal to the total SL thickness, resulting in a linear dependence between k and N.
Figure 3. Phonon engineering in superlattices. Experimental k as a function of: (a) period thickness of (TiNiSn):(HfNiSn) half-Heusler superlattices, (b) number of periods of GaAs/AlAs superlattices. Adapted from Holuj et al. [59] and Luckynova et al., respectively. (a) The crossover between coherent-incoherent (wave-particle) regimes is observed as a minimum in k vs. dSL, while in (b), the linearity of the k vs. N suggests that phonon heat conduction is coherent.
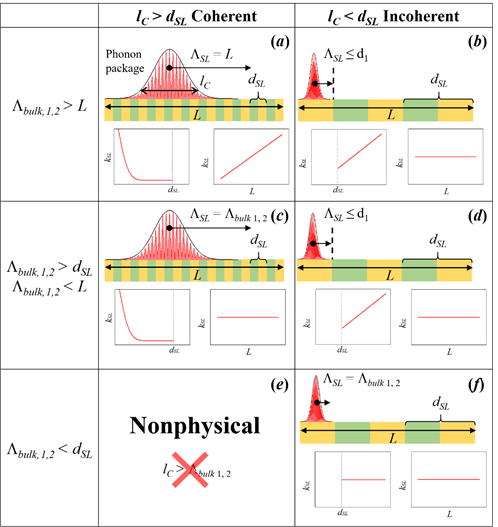
As we mentioned above, the concept of coherency cannot be applied directly in case of heat conduction because the thermal transport involves all excited phonons of the structure. However, Latour et al. showed that coherence can be formalized in other physical fields as correlation, e.g., the spatial coherence of the light can be expressed in terms of spatial correlations of electromagnetic fields. Inspired by this theory, Latour et al. extended this concept to the thermal phonons in superlattices. They postulated that the spatial phonon coherence length (lC) can be related to the spatial correlations of the atomic displacement fluctuations at equilibrium. The authors noted that if two atoms separated by a distance l and oscillating with a given phase and frequency (i.e., nonrandom), their motion is correlated. Hence, the finite spatial extension in which this correlation remains preserved is defined as spatial coherence length lC. This correlation arises from the presence of phonon wave packets composed by atoms vibrating in phase. Using this approach, the authors were able to distinguish different regimes of heat conduction characterized by the coherent length (lC), mean free path of the packet (Λ), period thickness (dSL) and total thickness of the superlattice (L). Then, the nature of the thermal transport will be given by the combination of these parameters as is shown in Figure 4. From the figure we can note that when lC > dSL (Figure 4a,c), the phonon transport is coherent. However, lC cannot be larger than the bulk mean free path (lC ≥ Λbulk, see Figure 4e). The wave package cannot travel a distance larger or equal to its spatial extension without scattering, i.e., it is a nonphysical phenomenon. For each of the rest of the cases shown in the figure, two trends for the thermal conductivity are depicted: one as a function of the dSL with a constant L and as a function of L with constant dSL. The crossover of thermal conductivity happens in Figure 4b,d,f. In these cases, the thermal conductivity becomes independent of the system size and increases with the SL period.
To observe coherent thermal transport, it is necessary that the incoming thermal wave retains its phase after it has been reflected or transmitted across the interface. This implies that the scattering mechanisms should not be purely diffusive, otherwise the phase information will be destroyed. Consequently, the presence of atomically smooth interfaces becomes mandatory. Although numerical simulations carried out by Qui et al. found the same linear dependence in rough periodic and aperiodic Si:Ge SLs [60], the results of their simulations were associated to the low interface densities and weak disorder scattering. Under these conditions, the dominant thermal phonons would not be affected by the disorder and could ballistically transverse the SLs regardless of aperiodicity or interface roughness. Similar results were found by Wang et al. [61] and Chakraborty et al. [62] in rough periodic SLs and random multilayer structures (RML) made of artificial atoms. Both simulations showed the same linear-like behavior of k⊥ vs. N. However, the absence of a minimum in k⊥ as a function of dSL in the simulations performed by Wang et al. suggest a ballistic phonon transport rather than coherent effects [61].
Figure 4. (a–f) Schematic representation of coherent and incoherent thermal transport in superlattices (adapted from Latour et al. ).
On the other hand, the introduction of very small-periods (10s of nm) have also shown a large impact on lowering k. Values close or smaller than the amorphous limit of one (or both) component of the SLs have been reported. Costescu et al. [63], Pernot et al. [64], and Chavez-Angel et al. [65] measured cross-plane thermal conductivity values (k⊥) below the amorphous limit of Al2O3, Si, and HfNiSn in Al2O3:W, SiGe:Si and HfNiSn:TiNiSn SLs, respectively. Niemelä et al. [66] also overtook the amorphous limit of TiO2 using organic-inorganic (TiO2):(Ti–O–C6H4–O) SLs.
Ultralow values of k were also reported by Juntunen et al. [67] in aperiodic Si:Ge SLs. The authors explained their observation in terms of wide range Anderson localization, which leads to a destructive interference of coherent phonons and consequently a drastic reduction of k by quenching the wave transport under structural disorder. Phonon localization was also reported by Luckynova et al. [68] using GaAs/AlAs superlattices with 8 and 25% of ErAs nanodots randomly distributed at the interfaces. They observed peaks in the normalized k of SLs as function of number of periods at 30 K and 50 K for 25% ErAs sample. Their observations were supported by theoretical calculations and explained in terms of a new heat conduction mechanism related to the presence of phonon localization in these SLs.
2.2 Two-Dimensional Materials
2.2.1. Graphene
The emergence of graphene has provided with a platform for the study of 2D phonon transport [69][70][71][72] and, at the same time, it’s extremely high thermal conductivity has driven applications in thermal management [73] and energy conversion [74]. Experimental studies have shown the possibility of tuning graphene’s thermal properties with different methods such as the control of isotope composition [75], metal deposition [76], introduction of defects [77][78][79], and orienting the grain size in polycrystalline graphene [80][81][82].
The development of methods for labelling [83] and growing [84] large grain-size monolayer graphene with regions of different concentrations of 12C and 13C has made possible the study of the impact of isotope concentration on the thermal properties. It was found that the k of suspended isotopically pure 12C (0.01% 13C) graphene can reach values higher than 4000 W m–1 K–1 close to room temperature (T≈320 K), which is more than a factor of two higher than the value of k in graphene sheets with an equal composition of 12C and 13C. In addition, Malekpour et al. found that as the defect density in suspended graphene increased from 2.0 × 1010 cm−2 to 1.8 × 1011 cm−2 the thermal conductivity decreases more than a factor of ∼4 near room temperature. The defects in this work were induced by irradiating graphene with a low-energy electron beam (20 keV). A different study also used oxygen plasma treatment to induce defects in suspended graphene and reduce its thermal conductivity more than 90%.
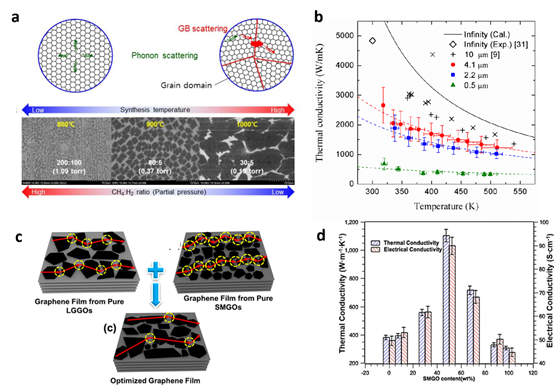
Moreover, the CVD method allows the growth of polycrystalline suspended single-layered graphene with controlled grain sizes by changing growth conditions (cf. Figure 5a). The k of the polycrystalline suspended graphene samples was found to decrease with decreasing grain size with a reduction up to a factor of ∼5 at 300 K for grain sizes of 0.5 µm. In addition, there is an evident vanishing of the k vs. T dependence with decreasing grain size (cf. Figure 5b). Here, and similarly to the effect seen in Figure 1e for Si PnCs, the increased phonon boundary scattering with decreasing grain size competes with the temperature dependent phonon-phonon scattering as mechanism to reduce the thermal transport. Since the earliest measurements on graphene, it is well known that the boundary interaction between graphene and an adjacent dielectric such as SiO2 [85] has a large degradation effect on the thermal conductivity. The drastic reduction was attributed to the damping of the acoustic phonons of graphene in general, and of the flexural acoustic phonons in particular, owing to the scattering in the graphene-SiO2 rough interface and the symmetry breaking by the presence of the substrate [86]. The suppression of the in-plane thermal conductivity is even more drastic when graphene is encased within silicon dioxide layers, showing a thermal conductivity value below 160 W m–1 K–1 at room temperature [87].
Figure 5. Phonon engineering in graphene. (a) Schematic illustration of the scattering mechanisms in polycrystalline graphene, i.e., phonon-phonon scattering and grain boundary scattering, and SEM images of samples with different nucleation densities. (b) The k as a function of the measured temperature for suspended graphene samples with grain sizes of 0.5, 2.2 and 4.1 nm. The symbol “◇” represents the k of exfoliated graphene. The k of “X” were measured for the suspended graphene on the hole of 9.7 μm in air and the k of “+” were measured for the suspended graphene on the hole of 8 μm in vacuum condition. (c) Schematics of the structure of the graphene films with different sized graphene oxides (large and small size graphene oxide: LGGO and SMGO, respectively) and (d) thermal and electrical conductivities of the graphene oxide films with different contents of small-sized graphene oxides (SMGO). (a,b) Reproduced with permission from [81]. Copyright American Chemical Society, 2017. (c,d) Reproduced with permission from [88]. Copyright American Chemical Society, 2020.
Other works have reported the use of hydrogen-bonded graphene-polymer interfaces [89] or functionalized self-assembled monolayers on graphene [90] to enhance the thermal boundary conductance (TBC) up to an order of magnitude. In addition, graphene-polymer composites with enhanced cross-plane thermal conductivity have been successfully engineered, showing their potential to be used as thermal interface materials [91]. Moreover, Kim et al. measured significant changes in the TBC of graphene-metal interfaces by generating physical and chemical defects [92] while Hopkins et al. used chemical adsorption on the graphene surface through plasma oxygen in order to control the heat flow across metal-graphene interfaces [93]. The heat transport across Al/graphene interfaces increased by a factor of ∼2 after the oxygen exposure of the graphene due to the enhancement of the bond strength between the Al and graphene atoms.
Furthermore, thermal measurements on graphene laminate films on polyethylene terephthalate substrates have also indicated that the average size and the alignment of graphene flakes on the substrate are key parameters defining the heat conduction [94]. Finally, thermally conductive graphene films with an in-plane thermal conductivity up to 1102.62 Wm–1K–1 have recently been produced by simple chemical reduction of graphene oxide. The structure of the graphene films with different sized graphene oxides is illustrated in Figure 5c. The graphene films with equal percentage of small (SMGO) and large sized graphene oxides (LSGO) showed minimized phonon scattering and maximum k, as is shown in Figure 5d.
2.2.2. Transition Metal Dichalcogenides and 2D Heterojunctions
Significant efforts have been made to tailor the thermal conductivity of transition metal dichalcogenides (TMDC) materials with promising thermoelectric performance. Starting with the MoS2, a continuously tuning of the thermal conductivity of suspended exfoliated (few layers) MoS2 flakes was demonstrated by exposure to a mild oxygen plasma [95]. The value of the in-plane thermal conductivity underwent a sharp drop down to values of the amorphous phase. In a recent experimental study, Li et al., showed that the in-plane thermal conductivity of monolayer crystals of MoS2 with isotopically enriched oxide precursors can be enhanced by ∼50% compared with the MoS2 synthesized using mixed Mo isotopes from naturally occurring molybdenum oxide [96]. Furthermore, suspended polycrystalline MoS2 nanofilms with average grain sizes of a few nanometers also have been realized by using a new polymer- and residue-free wet transfer method, where a strong reduction of the in-plane thermal conductivity was found due to scattering of phonons on nanoscale grain boundaries [97]. The same group later systematically studied the impact of the grain orientation on the thermal conductivity of supported polycrystalline ultrathin films of MoS2. [98] The lowest k value (0.27 Wm–1K–1) was obtained in a polycrystalline sample formed by a combination of horizontally and vertically oriented grains in similar proportion.
Different from MoS2, Chen et al. studied the k anisotropy between the zigzag and armchair axes in suspended Td-WTe2 samples of different thicknesses. They found that as the 2D layer thickness decreases, the phonon-boundary scattering increases faster along the armchair direction, resulting in stronger anisotropy. Furthermore, recent studies showed that the thermal conductivity of monolayer WS2 (32 Wm–1K–1) [99] is comparable to the thermal conductivity of monolayer MoS2 and that is possible to achieve an ultra-low cross-plane thermal conductivity value (0.05 Wm–1K–1) in disordered WSe2 sheets [100]. Moreover, it was found that the thermal conductivity of a 45 nm thick TaSe2 film decreased almost 50% compared to its bulk value [101].
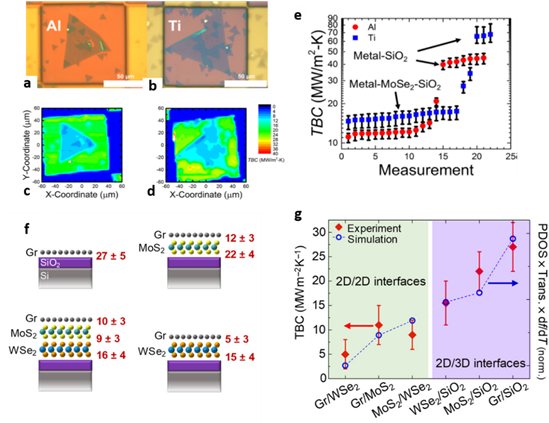
Progress has also been made in engineering van der Waals (vdW) heterostructures or interfaces consisting of stacks of 2D monolayers with different materials in the in-plane and out-of-plane direction. Understanding and controlling the transport of thermal phonons in such nanostructures is necessary for the effective thermal management of devices based on TMDC materials. Therefore, there are currently significant experimental efforts towards the investigation of the interfacial thermal property of 2D heterojunctions. In particular, the majority of the experimental studies are focused on studying different ways to increase the TBC of 2D interfaces by forming heterojunctions consisting of TMDC materials and graphene or thin metal layers [102][103]. For instance, Brown et al. studied heat transport across different metal-TMDC heterojunctions [102]. They found a higher TBC value across Ti−MoSe2−SiO2 interfaces compared to Al−MoSe2−SiO2 due to the better interlayer adhesion between Ti and MoSe2 atoms. Figure 6a–d show the probed regions of these interfaces and thermal boundary conductance maps, respectively. A summary of the TBC values across different MoSe2-based interfaces are shown in Figure 6e.
Figure 6. Phonon engineering in TMDC-based interfaces. Optical images showing the probed region of (a) Al−MoSe2−SiO2 and (b) Ti−MoSe2−SiO2 interfaces. (c,d) thermal boundary conductance (TBC) maps of the Al and Ti covered regions of the sample obtained by using time-domain thermoreflectance method (TDTR). (e) TBC values obtained at several positions across MoSe2 islands. (f) Schematics of TBCs measured across heterostructures consisting of graphene (Gr), Gr/ MoS2, Gr/WSe2, and Gr/MoS2/WSe2. (g) Measured TBC values of 2D/2D and 2D/3D (with SiO2) interfaces (red diamonds, left axis) and calculated values (open blue circles, right axis). The TBC were obtained by using single Laser Raman thermometry technique. (a-e) Reproduced with permission from [102]. Copyright American Chemical Society, 2019. (f,g) Reproduced with permission from [104]. Copyright American Institute of Physics, 2014.
On the other hand, when thermal isolation is desired, the engineering of interfaces that exhibit high thermal resistance is highly desirable. For example, a recent study demonstrated that ultrathin trilayer heterostructure consisting of stacks of monolayer graphene, MoS2, and WSe2 exhibit ultra-high interface thermal resistance resulting in an effective thermal conductivity lower than air at 300 K [104]. A schematic of the different heterostructures investigated in this work and the measured TBC values are presented in Figure 6f,g, respectively.
References
- Hamann, H.F.; Weger, A.; Lacey, J.A.; Hu, Z.; Bose, P.; Cohen, E.; Wakil, J. Hotspot-Limited Microprocessors: Direct Temperature and Power Distribution Measurements. IEEE J. Solid State Circuits 2007, 42, 56–65, doi:10.1109/jssc.2006.885064.
- Zhang, Z.; Ouyang, Y.; Cheng, Y.; Chen, J.; Li, N.; Zhang, G. Size-dependent phononic thermal transport in low-dimensional nanomaterials. Phys. Rep. 2020, 860, 1–26, doi:10.1016/j.physrep.2020.03.001.
- Wang, C.; Guo, J.; Dong, L.; Aiyiti, A.; Xu, X.; Li, B. Superior thermal conductivity in suspended bilayer hexagonal boron nitride. Sci. Rep. 2016, 6, 25334, doi:10.1038/srep25334.
- Lee, W.; Kim, K.; Jeong, W.; Zotti, L.A.; Pauly, F.; Cuevas, J.C.; Reddy, P. Heat dissipation in atomic-scale junctions. Nat. Cell Biol. 2013, 498, 209–212, doi:10.1038/nature12183.
- Srivastava, G.P.; Kresin, V. The Physics of Phonons. Phys. Today 1991, 44, 75–76, doi:10.1063/1.2810367.
- Ziman, J.M. Electrons and Phonons: The Theory of Transport Phenomena in Solids; Oxford University Press: New York, NY, USA, 1960.
- Cuffe, J.; Chávez, E.; Shchepetov, A.; Chapuis, P.-O.; El Boudouti, E.H.; Alzina, F.; Kehoe, T.; Gomis-Bresco, J.; Dudek, D.; Pennec, Y.; et al. Phonons in Slow Motion: Dispersion Relations in Ultrathin Si Membranes. Nano Lett. 2012, 12, 3569–3573, doi:10.1021/nl301204u.
- Zou, J.; Balandin, A. Phonon heat conduction in a semiconductor nanowire. J. Appl. Phys. 2001, 89, 2932–2938, doi:10.1063/1.1345515.
- Zou, J.; Lange, X.; Richardson, C. Lattice thermal conductivity of nanoscale AlN∕GaN∕AlN heterostructures: Effects of partial phonon spatial confinement. J. Appl. Phys. 2006, 100, 104309, doi:10.1063/1.2365380.
- Balandin, A.; Wang, K.L. Significant decrease of the lattice thermal conductivity due to phonon confinement in a free-standing semiconductor quantum well. Phys. Rev. B 1998, 58, 1544–1549, doi:10.1103/physrevb.58.1544.
- Malhotra, A.; Maldovan, M. Phononic pathways towards rational design of nanowire heat conduction. Nanotechnology 2019, 30, 372002, doi:10.1088/1361-6528/ab261d.
- Maldovan, M. Phonon wave interference and thermal bandgap materials. Nat. Mater. 2015, 14, 667–674, doi:10.1038/nmat4308.
- Luckyanova, M.N.; Garg, J.; Esfarjani, K.; Jandl, A.; Bulsara, M.T.; Schmidt, A.J.; Minnich, A.J.; Chen, S.; Dresselhaus, M.S.; Ren, Z.; et al. Coherent Phonon Heat Conduction in Superlattices. Science 2012, 338, 936–939, doi:10.1126/science.1225549.
- Ravichandran, J.; Yadav, A.K.; Cheaito, R.; Rossen, P.B.; Soukiassian, A.; Suresha, S.J.; Duda, J.C.; Foley, B.M.; Lee, C.-H.; Zhu, Y.; et al. Crossover from incoherent to coherent phonon scattering in epitaxial oxide superlattices. Nat. Mater. 2014, 13, 168–172, doi:10.1038/nmat3826.
- Maire, J.; Anufriev, R.; Yanagisawa, R.; Ramiere, A.; Volz, S.; Nomura, M. Heat conduction tuning by wave nature of phonons. Sci. Adv. 2017, 3, e1700027, doi:10.1126/sciadv.1700027.
- Anufriev, R.; Ramiere, A.; Maire, J.; Nomura, M. Heat guiding and focusing using ballistic phonon transport in phononic nanostructures. Nat. Commun. 2017, 8, 15505, doi:10.1038/ncomms15505.
- Asheghi, M.; Leung, Y.K.; Wong, S.S.; Goodson, K.E. Phonon-boundary scattering in thin silicon layers. Appl. Phys. Lett. 1997, 71, 1798–1800, doi:10.1063/1.119402.
- El Sachat, A. Characterization of Nanostructured Materials for Thermal Conduction and Heat Transfer Control. Ph.D. Thesis, Universitat Automona de Barcelona, Barcelona, Spain, 2017.
- Reparaz, J.S.; Chavez-Angel, E.; Wagner, M.R.; Graczykowski, B.; Gomis-Bresco, J.; Alzina, F.; Sotomayor Torres, C.M. A novel contactless technique for thermal field mapping and thermal conductivity determination: Two-Laser Raman Thermometry. Rev. Sci. Instrum. 2014, 85, 034901, doi:10.1063/1.4867166.
- Marconnet, A.; Asheghi, M.; Goodson, K.E. From the Casimir Limit to Phononic Crystals: 20 Years of Phonon Transport Studies Using Silicon-on-Insulator Technology. J. Heat Transf. 2013, 135, 061601, doi:10.1115/1.4023577.
- Chen, Y.; Peng, B.; Cong, C.; Shang, J.; Wu, L.; Yang, W.; Zhou, J.; Yu, P.; Zhang, H.; Wang, Y.; et al. In-Plane Anisotropic Thermal Conductivity of Few-Layered Transition Metal Dichalcogenide Td-WTe2. Adv. Mater. 2019, 31, e1804979, doi:10.1002/adma.201804979.
- Nomura, M.; Nakagawa, J.; Kage, Y.; Maire, J.; Moser, D.; Paul, O. Thermal phonon transport in silicon nanowires and two-dimensional phononic crystal nanostructures. Appl. Phys. Lett. 2015, 106, 143102, doi:10.1063/1.4917036.
- Graczykowski, B.; El Sachat, A.; Reparaz, J.S.; Sledzinska, M.; Wagner, M.R.; Chavez-Angel, E.; Wu, Y.; Volz, S.; Alzina, F.; Sotomayor Torres, C.M Thermal conductivity and air-mediated losses in periodic porous silicon membranes at high temperatures. Nat. Commun. 2017, 8, 1–9, doi:10.1038/s41467-017-00115-4.
- Anufriev, R.; Maire, J.; Nomura, M. Reduction of thermal conductivity by surface scattering of phonons in periodic silicon nanostructures. Phys. Rev. B 2016, 93, 045411, doi:10.1103/physrevb.93.045411.
- Yanagisawa, R.; Maire, J.; Ramiere, A.; Anufriev, R.; Nomura, M. Impact of limiting dimension on thermal conductivity of one-dimensional silicon phononic crystals. Appl. Phys. Lett. 2017, 110, 133108, doi:10.1063/1.4979080.
- Iskandar, A.; Gwiazda, A.; Huang, Y.; Kazan, M.; Bruyant, A.; Tabbal, M.; Lerondel, G. Modification of the phonon spectrum of bulk Si through surface nanostructuring. J. Appl. Phys. 2016, 120, 095106, doi:10.1063/1.4962208.
- Anufriev, R.; Yanagisawa, R.; Nomura, M. Aluminium nanopillars reduce thermal conductivity of silicon nanobeams. Nanoscale 2017, 9, 15083–15088, doi:10.1039/c7nr05114j.
- Huang, X.; Ohori, D.; Yanagisawa, R.; Anufriev, R.; Samukawa, S.; Nomura, M. Coherent and Incoherent Impacts of Nanopillars on the Thermal Conductivity in Silicon Nanomembranes. ACS Appl. Mater. Interfaces 2020, 12, 25478–25483, doi:10.1021/acsami.0c06030.
- Puurtinen, T.A.; Maasilta, I.J. Low-Temperature Coherent Thermal Conduction in Thin Phononic Crystal Membranes. Crystals 2016, 6, 72, doi:10.3390/cryst6060072.
- Tian, Y.; Puurtinen, T.A.; Geng, Z.; Maasilta, I.J. Minimizing Coherent Thermal Conductance by Controlling the Periodicity of Two-Dimensional Phononic Crystals. Phys. Rev. Appl. 2019, 12, 014008, doi:10.1103/physrevapplied.12.014008.
- Zen, N.; Puurtinen, T.A.; Isotalo, T.J.; Chaudhuri, S.; Maasilta, I.J. Engineering thermal conductance using a two-dimensional phononic crystal. Nat. Commun. 2014, 5, 3435, doi:10.1038/ncomms4435.
- Wagner, M.R.; Graczykowski, B.; Reparaz, J.S.; El Sachat, A.; Sledzinska, M.; Alzina, F.; Sotomayor Torres, C.M Two-Dimensional Phononic Crystals: Disorder Matters. Nano Lett. 2016, 16, 5661–5668, doi:10.1021/acs.nanolett.6b02305.
- Venkatasubramanian, R. Lattice thermal conductivity reduction and phonon localizationlike behavior in superlattice structures. Phys. Rev. B 2000, 61, 3091–3097, doi:10.1103/physrevb.61.3091.
- Xie, G.; Ding, D.; Zhang, G. Phonon coherence and its effect on thermal conductivity of nanostructures. Adv. Phys. X 2018, 3, 1480417, doi:10.1080/23746149.2018.1480417.
- Lee, J.; Lee, W.; Wehmeyer, G.; Dhuey, S.; Olynick, D.L.; Cabrini, S.; Dames, C.; Urban, J.J.; Yang, P. Investigation of phonon coherence and backscattering using silicon nanomeshes. Nat. Commun. 2017, 8, 14054, doi:10.1038/ncomms14054.
- Yu, J.-K.; Mitrovic, S.; Tham, D.; O Varghese, J.; Heath, J.R. Reduction of thermal conductivity in phononic nanomesh structures. Nat. Nanotechnol. 2010, 5, 718–721, doi:10.1038/nnano.2010.149.
- Hopkins, P.E.; Reinke, C.M.; Su, M.F.; Olsson, R.H.; Shaner, E.A.; Leseman, Z.C.; Serrano, J.R.; Phinney, L.M.; El-Kady, I. Reduction in the Thermal Conductivity of Single Crystalline Silicon by Phononic Crystal Patterning. Nano Lett. 2011, 11, 107–112, doi:10.1021/nl102918q.
- Alaie, S.; Goettler, D.F.; Su, M.; Leseman, Z.C.; Reinke, C.; El-Kady, I. Thermal transport in phononic crystals and the observation of coherent phonon scattering at room temperature. Nat. Commun. 2015, 6, 7228, doi:10.1038/ncomms8228.
- Jain, A.; Yu, Y.-J.; McGaughey, A.J.H. Phonon transport in periodic silicon nanoporous films with feature sizes greater than 100 nm. Phys. Rev. B 2013, 87, 87, doi:10.1103/physrevb.87.195301.
- Ravichandran, N.K.; Minnich, A.J. Coherent and incoherent thermal transport in nanomeshes. Phys. Rev. B 2014, 89, 89, doi:10.1103/physrevb.89.205432.
- Latour, B.; Volz, S.; Chalopin, Y. Microscopic description of thermal-phonon coherence: From coherent transport to diffuse interface scattering in superlattices. Phys. Rev. B 2014, 90, 014307, doi:10.1103/physrevb.90.014307.
- Xiao, Y.; Xu, D.; Medina, F.J.; Wang, S.; Hao, Q. Thermal studies of nanoporous thin films with added periodic nanopores—a new approach to evaluate the importance of phononic effects. Mater. Today Phys. 2020, 12, 100179, doi:10.1016/j.mtphys.2020.100179.
- Sledzinska, M.; Graczykowski, B.; Maire, J.; Chavez‐Angel, E.; Sotomayor Torres, C.M; Alzina, F. 2D Phononic Crystals: Progress and Prospects in Hypersound and Thermal Transport Engineering. Adv. Funct. Mater. 2020, 30, 1904434, doi:10.1002/adfm.201904434.
- Li, D.; Wu, Y.; Kim, P.; Shi, L.; Yang, P.; Majumdar, A. Thermal conductivity of individual silicon nanowires. Appl. Phys. Lett. 2003, 83, 2934–2936, doi:10.1063/1.1616981.
- Swinkels, M.Y.; Van Delft, M.R.; Oliveira, D.S.; Cavalli, A.A.; Zardo, I.; Van Der Heijden, R.W.; Bakkers, E.P.A.M. Diameter dependence of the thermal conductivity of InAs nanowires. Nanotechnology 2015, 26, 385401, doi:10.1088/0957-4484/26/38/385401.
- Ren, P.; Zhu, X.; Han, J.; Xu, J.; Ma, L.; Li, H.; Zhuang, X.; Zhou, H.; Zhang, Q.; Xia, M.; et al. Synthesis and Diameter-dependent Thermal Conductivity of InAs Nanowires. Nano Micro Lett. 2014, 6, 301–306, doi:10.1007/s40820-014-0002-8.
- Lee, J.; Lee, W.; Lim, J.; Yu, Y.; Kong, Q.; Mattox, T.M.; Yang, P. Thermal Transport in Silicon Nanowires at High Temperature up to 700 K. Nano Lett. 2016, 16, 4133–4140, doi:10.1021/acs.nanolett.6b00956.
- Hsiao, T.-K.; Chang, H.-K.; Liou, S.-C.; Chu, M.-W.; Lee, S.-C.; Chang, C.-W. Observation of room-temperature ballistic thermal conduction persisting over 8.3 µm in SiGe nanowires. Nat. Nanotechnol. 2013, 8, 534–538, doi:10.1038/nnano.2013.121.
- Anufriev, R.; Gluchko, S.; Volz, S.; Nomura, M. Quasi-Ballistic Heat Conduction due to Lévy Phonon Flights in Silicon Nanowires. ACS Nano 2018, 12, 11928–11935, doi:10.1021/acsnano.8b07597.
- Vakulov, D.; Gireesan, S.; Swinkels, M.Y.; Chavez, R.; Vogelaar, T.J.; Torres, P.; Campo, A.; De Luca, M.; Verheijen, M.A.; Koelling, S.; et al. Ballistic Phonons in Ultrathin Nanowires. Nano Lett. 2020, 20, 2703–2709, doi:10.1021/acs.nanolett.0c00320.
- Wang, L.; Li, B. Thermal Logic Gates: Computation with Phonons. Phys. Rev. Lett. 2007, 99, 177208, doi:10.1103/physrevlett.99.177208.
- Sklan, S.R. Splash, pop, sizzle: Information processing with phononic computing. AIP Adv. 2015, 5, 053302, doi:10.1063/1.4919584.
- Wingert, M.C.; Chen, Z.C.Y.; Dechaumphai, E.; Moon, J.; Kim, J.-H.; Xiang, J.; Chen, R. Thermal Conductivity of Ge and Ge–Si Core–Shell Nanowires in the Phonon Confinement Regime. Nano Lett. 2011, 11, 5507–5513, doi:10.1021/nl203356h.
- Juntunen, T.; Koskinen, T.; Khayrudinov, V.; Haggren, T.; Jiang, H.; Lipsanen, H.; Tittonen, I.J. Thermal conductivity suppression in GaAs–AlAs core–shell nanowire arrays. Nanoscale 2019, 11, 20507–20513, doi:10.1039/c9nr06831g.
- Zhao, Y.; Liu, D.; Chen, J.; Zhu, L.; Belianinov, A.; Ovchinnikova, O.S.; Unocic, R.R.; Burch, M.J.; Kim, S.; Hao, H.; et al. Engineering the thermal conductivity along an individual silicon nanowire by selective helium ion irradiation. Nat. Commun. 2017, 8, 15919, doi:10.1038/ncomms15919.
- Mukherjee, S.; Givan, U.; Senz, S.; Bergeron, A.; Francoeur, S.; De La Mata, M.; Arbiol, J.; Sekiguchi, T.; Itoh, K.M.; Isheim, D.; et al. Phonon Engineering in Isotopically Disordered Silicon Nanowires. Nano Lett. 2015, 15, 3885–3893, doi:10.1021/acs.nanolett.5b00708.
- Mukherjee, S.; Givan, U.; Senz, S.; De La Mata, M.; Arbiol, J.; Moutanabbir, O. Reduction of Thermal Conductivity in Nanowires by Combined Engineering of Crystal Phase and Isotope Disorder. Nano Lett. 2018, 18, 3066–3075, doi:10.1021/acs.nanolett.8b00612.
- Narayanaamurti, V. Phonon Optics and Phonon Propagation in Semiconductors. Science 1981, 213, 717–723, doi:10.1126/science.213.4509.717.
- Hołuj, P.; Euler, C.; Balke, B.; Kolb, U.; Fiedler, G.; Müller, M.M.; Jaeger, T.; Angel, E.C.; Kratzer, P.; Jakob, G. Reduced thermal conductivity of TiNiSn/HfNiSn superlattices. Phys. Rev. B 2015, 92, 125436, doi:10.1103/physrevb.92.125436.
- Qiu, B.; Chen, G.; Tian, Z. Effects of Aperiodicity and Roughness on Coherent Heat Conduction in Superlattices. Nanoscale Microscale Thermophys. Eng. 2015, 19, 272–278, doi:10.1080/15567265.2015.1102186.
- Wang, Y.; Gu, C.; Ruan, X. Optimization of the random multilayer structure to break the random-alloy limit of thermal conductivity. Appl. Phys. Lett. 2015, 106, 073104, doi:10.1063/1.4913319.
- Chakraborty, P.; Cao, L.; Wang, Y. Ultralow Lattice Thermal Conductivity of the Random Multilayer Structure with Lattice Imperfections. Sci. Rep. 2017, 7, 1–8, doi:10.1038/s41598-017-08359-2.
- Costescu, R.M.; Cahill, D.G.; Fabreguette, F.H.; Sechrist, Z.A.; George, S.M. Ultra-Low Thermal Conductivity in W/Al2O3 Nanolaminates. Science 2004, 303, 989–990, doi:10.1126/science.1093711.
- Pernot, G.; Stoffel, M.; Savić, I.; Pezzoli, F.; Chen, P.; Savelli, G.; Jacquot, A.; Schumann, J.; Denker, U.; Mönch, I.; et al. Precise control of thermal conductivity at the nanoscale through individual phonon-scattering barriers. Nat. Mater. 2010, 9, 491–495, doi:10.1038/nmat2752.
- Chavez-Angel, E.; Reuter, N.; Komar, P.; Heinz, S.; Kolb, U.; Kleebe, H.-J.; Jakob, G. Subamorphous Thermal Conductivity of Crystalline Half-Heusler Superlattices. Nanoscale Microscale Thermophys. Eng. 2018, 23, 1–9, doi:10.1080/15567265.2018.1505987.
- Niemelä, J.-P.; Giri, A.; Hopkins, P.E.; Karppinen, M. Ultra-low thermal conductivity in TiO2:C superlattices. J. Mater. Chem. A 2015, 3, 11527–11532, doi:10.1039/c5ta01719j.
- Juntunen, T.; Vänskä, O.; Tittonen, I. Anderson Localization Quenches Thermal Transport in Aperiodic Superlattices. Phys. Rev. Lett. 2019, 122, 105901, doi:10.1103/physrevlett.122.105901.
- Luckyanova, M.N.; Mendoza, J.; Lu, H.; Song, B.; Huang, S.; Zhou, J.; Li, M.; Dong, Y.; Zhou, H.; Garlow, J.; et al. Phonon localization in heat conduction. Sci. Adv. 2018, 4, eaat9460, doi:10.1126/sciadv.aat9460.
- Xu, X.; Chen, J.; Li, B. Phonon thermal conduction in novel 2D materials. J. Phys. Condens. Matter 2016, 28, 483001, doi:10.1088/0953-8984/28/48/483001.
- Cepellotti, A.; Fugallo, G.; Paulatto, L.; Lazzeri, M.; Mauri, F.; Marzari, N. Phonon hydrodynamics in two-dimensional materials. Nat. Commun. 2015, 6, 6400, doi:10.1038/ncomms7400.
- Balandin, A.A. Phononics of Graphene and Related Materials. ACS Nano 2020, 14, 5170–5178, doi:10.1021/acsnano.0c02718.
- Nika, D.L.; Balandin, A.A. Phonons and thermal transport in graphene and graphene-based materials. Rep. Prog. Phys. 2017, 80, 036502, doi:10.1088/1361-6633/80/3/036502.
- Fu, Y.; Hansson, J.; Liu, Y.; Chen, S.; Zehri, A.; Samani, M.K.; Wang, N.; Ni, Y.; Zhang, Y.; Zhang, Z.-B.; et al. Graphene related materials for thermal management. 2D Mater. 2019, 7, 012001, doi:10.1088/2053-1583/ab48d9.
- Song, H.; Liu, J.; Liu, B.; Wu, J.; Cheng, H.-M.; Kang, F. Two-Dimensional Materials for Thermal Management Applications. Joule 2018, 2, 442–463, doi:10.1016/j.joule.2018.01.006.
- Chen, S.; Wu, Q.; Mishra, C.; Kang, J.; Zhang, H.; Cho, K.; Cai, W.; Balandin, A.A.; Ruoff, R.S. Thermal conductivity of isotopically modified graphene. Nat. Mater. 2012, 11, 203–207, doi:10.1038/nmat3207.
- Wang, J.; Zhu, L.; Chen, J.; Li, B.; Thong, J.T.L. Suppressing Thermal Conductivity of Suspended Tri-layer Graphene by Gold Deposition. Adv. Mater. 2013, 25, 6884–6888, doi:10.1002/adma.201303362.
- Malekpour, H.; Ramnani, P.; Srinivasan, S.; Balasubramanian, G.; Nika, D.L.; Mulchandani, A.; Lake, R.K.; Balandin, A.A. Thermal conductivity of graphene with defects induced by electron beam irradiation. Nanoscale 2016, 8, 14608–14616, doi:10.1039/c6nr03470e.
- Zhao, W.; Wang, Y.; Wu, Z.; Wang, W.; Bi, K.; Liang, Z.; Yang, J.; Chen, Y.; Xu, Z.; Ni, Z. Defect-Engineered Heat Transport in Graphene: A Route to High Efficient Thermal Rectification. Sci. Rep. 2015, 5, 11962, doi:10.1038/srep11962.
- Anno, Y.; Imakita, Y.; Takei, K.; Akita, S.; Arie, T. Enhancement of graphene thermoelectric performance through defect engineering. 2D Mater. 2017, 4, 025019, doi:10.1088/2053-1583/aa57fc.
- Ma, T.; Liu, Z.; Wen, J.; Gao, Y.; Ren, X.; Chen, H.; Jin, C.; Ma, X.-L.; Xu, N.; Cheng, H.-M.; et al. Tailoring the thermal and electrical transport properties of graphene films by grain size engineering. Nat. Commun. 2017, 8, 14486, doi:10.1038/ncomms14486.
- Lee, W.; Kihm, K.D.; Kim, H.G.; Shin, S.; Lee, C.; Park, J.S.; Cheon, S.; Kwon, O.M.; Lim, G.; Lee, W. In-Plane Thermal Conductivity of Polycrystalline Chemical Vapor Deposition Graphene with Controlled Grain Sizes. Nano Lett. 2017, 17, 2361–2366, doi:10.1021/acs.nanolett.6b05269.
- Limbu, T.B.; Hahn, K.R.; Mendoza, F.; Sahoo, S.; Razink, J.J.; Katiyar, R.S.; Weiner, B.R.; Morell, G. Grain size-dependent thermal conductivity of polycrystalline twisted bilayer graphene. Carbon 2017, 117, 367–375, doi:10.1016/j.carbon.2017.02.066.
- Li, X.; Cai, W.; Colombo, L.; Ruoff, R.S. Evolution of Graphene Growth on Ni and Cu by Carbon Isotope Labeling. Nano Lett. 2009, 9, 4268–4272, doi:10.1021/nl902515k.
- Li, X.; Magnuson, C.W.; Venugopal, A.; Tromp, R.M.; Hannon, J.B.; Vogel, E.M.; Colombo, L.; Ruoff, R.S. Large-Area Graphene Single Crystals Grown by Low-Pressure Chemical Vapor Deposition of Methane on Copper. J. Am. Chem. Soc. 2011, 133, 2816–2819, doi:10.1021/ja109793s.
- Seol, J.H.; Jo, I.; Moore, A.L.; Lindsay, L.; Aitken, Z.H.; Pettes, M.T.; Li, X.; Yao, Z.; Huang, R.; Broido, D.; et al. Two-Dimensional Phonon Transport in Supported Graphene. Science 2010, 328, 213–216, doi:10.1126/science.1184014.
- Qiu, B.; Ruan, X. Reduction of spectral phonon relaxation times from suspended to supported graphene. Appl. Phys. Lett. 2012, 100, 193101, doi:10.1063/1.4712041.
- Jang, W.; Chen, Z.; Bao, W.; Lau, C.N.; Dames, C. Thickness-Dependent Thermal Conductivity of Encased Graphene and Ultrathin Graphite. Nano Lett. 2010, 10, 3909–3913, doi:10.1021/nl101613u.
- Yang, G.; Yi, H.; Yao, Y.; Li, C.; Li, Z. Thermally Conductive Graphene Films for Heat Dissipation. ACS Appl. Nano Mater. 2020, 3, 2149–2155, doi:10.1021/acsanm.9b01955.
- Zhang, L.; Liu, L. Hierarchically hydrogen-bonded graphene/polymer interfaces with drastically enhanced interfacial thermal conductance. Nanoscale 2019, 11, 3656–3664, doi:10.1039/c8nr08760a.
- Zhang, L.; Liu, L. Polymeric Self-Assembled Monolayers Anomalously Improve Thermal Transport across Graphene/Polymer Interfaces. ACS Appl. Mater. Interfaces 2017, 9, 28949–28958, doi:10.1021/acsami.7b09605.
- Shahil, K.M.F.; Balandin, A.A. Graphene–Multilayer Graphene Nanocomposites as Highly Efficient Thermal Interface Materials. Nano Lett. 2012, 12, 861–867, doi:10.1021/nl203906r.
- Kim, J.; Khan, M.E.; Ko, J.-H.; Kim, J.H.; Lee, E.-S.; Suh, J.; Wu, J.; Kim, Y.-H.; Park, J.Y.; Lyeo, H.-K. Bimodal Control of Heat Transport at Graphene–Metal Interfaces Using Disorder in Graphene. Sci. Rep. 2016, 6, 34428, doi:10.1038/srep34428.
- Hopkins, P.E.; Baraket, M.; Barnat, E.V.; Beechem, T.E.; Kearney, S.P.; Duda, J.C.; Robinson, J.T.; Walton, S.G. Manipulating Thermal Conductance at Metal–Graphene Contacts via Chemical Functionalization. Nano Lett. 2012, 12, 590–595, doi:10.1021/nl203060j.
- Malekpour, H.; Chang, K.-H.; Chen, J.-C.; Lu, C.-Y.; Nika, D.L.; Novoselov, K.S.; Balandin, A.A. Thermal Conductivity of Graphene Laminate. Nano Lett. 2014, 14, 5155–5161, doi:10.1021/nl501996v.
- Aiyiti, A.; Hu, S.; Wang, C.; Xi, Q.; Cheng, Z.; Xia, M.; Ma, Y.; Wu, T.D.A.J.; Guo, J.; Wang, Q.; et al. Thermal conductivity of suspended few-layer MoS2. Nanoscale 2018, 10, 2727–2734, doi:10.1039/c7nr07522g.
- Li, X.; Zhang, J.; Puretzky, A.A.; Yoshimura, A.; Sang, X.; Cui, Q.; Li, Y.; Liang, L.; Ghosh, A.W.; Zhao, H.; et al. Isotope-Engineering the Thermal Conductivity of Two-Dimensional MoS2. ACS Nano 2019, 13, 2481–2489, doi:10.1021/acsnano.8b09448.
- Sledzinska, M.; Graczykowski, B.; Placidi, M.; Reig, D.S.; El Sachat, A.; Reparaz, J.S.; Alzina, F.; Mortazavi, B.; Quey, R.; Colombo, L.; et al. Thermal conductivity of MoS 2 polycrystalline nanomembranes. 2D Mater. 2016, 3, 035016, doi:10.1088/2053-1583/3/3/035016.
- Sledzinska, M.; Quey, R.; Mortazavi, B.; Graczykowski, B.; Placidi, M.; Reig, D.S.; Navarro-Urrios, D.; Alzina, F.; Colombo, L.; Roche, S.; et al. Record Low Thermal Conductivity of Polycrystalline MoS2 Films: Tuning the Thermal Conductivity by Grain Orientation. ACS Appl. Mater. Interfaces 2017, 9, 37905–37911, doi:10.1021/acsami.7b08811.
- Peimyoo, N.; Shang, J.; Yang, W.; Wang, Y.; Cong, C.; Yu, D.Y.W. Thermal conductivity determination of suspended mono- and bilayer WS2 by Raman spectroscopy. Nano Res. 2014, 8, 1210–1221, doi:10.1007/s12274-014-0602-0.
- Chiritescu, C.; Cahill, D.G.; Nguyen, N.; Johnson, D.; Bodapati, A.; Keblinski, P.; Zschack, P. Ultralow Thermal Conductivity in Disordered, Layered WSe2 Crystals. Science 2007, 315, 351–353, doi:10.1126/science.1136494.
- Yan, Z.; Jiang, C.; Pope, T.R.; Tsang, C.; Stickney, J.L.; Goli, P.; Renteria, J.; Salguero, T.T.; Balandin, A.A. Phonon and thermal properties of exfoliated TaSe2 thin films. J. Appl. Phys. 2013, 114, 204301, doi:10.1063/1.4833250.
- Brown, D.B.; Shen, W.; Li, X.; Xiao, K.; Geohegan, D.B.; Kumar, S. Spatial Mapping of Thermal Boundary Conductance at Metal–Molybdenum Diselenide Interfaces. ACS Appl. Mater. Interfaces 2019, 11, 14418–14426, doi:10.1021/acsami.8b22702.
- Chen, C.-C.; Li, Z.; Shi, L.; Wang, B. Thermal interface conductance across a graphene/hexagonal boron nitride heterojunction. Appl. Phys. Lett. 2014, 104, 081908, doi:10.1063/1.4866335.
- Vaziri, S.; Yalon, E.; Rojo, M.M.; Suryavanshi, S.V.; Zhang, H.; McClellan, C.J.; Bailey, C.S.; Smithe, K.K.H.; Gabourie, A.J.; Chen, V.; et al. Ultrahigh thermal isolation across heterogeneously layered two-dimensional materials. Sci. Adv. 2019, 5, eaax1325, doi:10.1126/sciadv.aax1325.