Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Angelos Alamanos
 -- 892 2024-02-08 04:51:54 |
2 formatted
Vicky Zhou
 Meta information modification 892 2024-02-08 04:55:10 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Alamanos, A.; Garcia, J.A. Optimization Examples for Water Allocation, Energy, Carbon Emissions, and Costs. Encyclopedia. Available online: https://encyclopedia.pub/entry/54891 (accessed on 10 May 2024).
Alamanos A, Garcia JA. Optimization Examples for Water Allocation, Energy, Carbon Emissions, and Costs. Encyclopedia. Available at: https://encyclopedia.pub/entry/54891. Accessed May 10, 2024.
Alamanos, Angelos, Jorge Andres Garcia. "Optimization Examples for Water Allocation, Energy, Carbon Emissions, and Costs" Encyclopedia, https://encyclopedia.pub/entry/54891 (accessed May 10, 2024).
Alamanos, A., & Garcia, J.A. (2024, February 08). Optimization Examples for Water Allocation, Energy, Carbon Emissions, and Costs. In Encyclopedia. https://encyclopedia.pub/entry/54891
Alamanos, Angelos and Jorge Andres Garcia. "Optimization Examples for Water Allocation, Energy, Carbon Emissions, and Costs." Encyclopedia. Web. 08 February, 2024.
Peer Reviewed
Optimization Examples for Water Allocation, Energy, Carbon Emissions, and Costs
This is a peer-reviewed entry published in Encyclopedia Journal, full entry can be found at 10.3390/encyclopedia4010022

The field of Water Resources Management (WRM) is becoming increasingly interdisciplinary, realizing its direct connections with energy, food, and social and economic sciences, among others. Computationally, this leads to more complex models, wherein the achievement of multiple goals is sought. Optimization processes have found various applications in such complex WRM problems. This entry considers the main factors involved in modern WRM, and puts them in a single optimization problem, including water allocation from different sources to different uses and non-renewable and renewable energy supplies, with their associated carbon emissions and costs. The entry explores the problem mathematically by presenting different optimization approaches, such as linear, fuzzy, dynamic, goal, and non-linear programming models. Furthermore, codes for each model are provided in Python, an open-source language. This entry has an educational character, and the examples presented are easily reproducible, so this is expected to be a useful resource for students, modelers, researchers, and water managers.

optimization water-energy carbon emissions economics linear programming fuzzy optimization dynamic optimization non-linear programming goal programming Python
The main themes of this encyclopaedia entry are an integrated resources management problem considering environmental and economic parameters, and its representation through different optimization types.

Integrated Water Resources Management Optimization Applications

Water Resources Management (WRM) involves all measures and actions that we apply to water resources (surface, groundwater, freshwater, and seawater), to convert or improve their status and cover the multiple needs of societies and ecosystems [1][2]. As one can imagine, WRM is subject to multiple factors (e.g., meteorological, natural, ecological, and socio-economic), and should take into account various water sources and different users, with different characteristics [3]. There are also multiple direct and indirect implications of WRM in the short and long term, applicable to multiple sectors (such as ecology, biodiversity, hydrology, economy, energy, industry, urban planning, policy, etc.) [4]. Integrated Water Resources Management (IWRM) acknowledges the intricate nature of WRM, encompassing various factors, stakeholders, and short- and long-term implications across multiple sectors. Thus, WRM is often meant to be a holistic and integrated process, by nature [5][6]. Since water resources utilization is connected with multiple other uses and activities, WRM deals with complex problems that must take into account many different variables reflecting this complexity (different sources, different users, and gains from using water, as mentioned). These complex problems have theoretically infinite management solutions. The achievement of WRM objectives under the various restrictions posed by their natural, social, economic, and regulatory aspects can be closely related to an optimization process approach that aims to find the optimum solution(s) under specific constraints [7]. This logic has been a useful approach for several aspects of WRM research and practice, with various applications [8][9], including water resources allocation [10][11][12], water infrastructure, irrigation networks, dams and reservoirs, hydropower works, etc. [13][14][15], hydrology and hydraulics [16][17][18], disaster analysis and management [19][20][21], water quality management [22][23][24][25], transboundary water management [26][27][28][29], policy/governance/development [30][31][32][33][34][35], Water-Energy-Food Nexus [36][37][38], and other cross-disciplinary fields such as hydro-economics, socio-hydrology, ecohydrology, etc. [39][40][41][42][43][44][45][46].

Optimization Logic

Optimization is a mathematical representation of a problem that we want to solve in the best possible way, satisfying many (often conflicting) objectives. The solutions of such problems are not evident or clearly standing out, so optimization formulates the problems in a structured way (mathematically), helping us solve them while quantifying the impacts of these solutions, or their trade-offs with the constraints of the problem [13].
An objective (goal) is selected for our problem and the optimal solution to the problem will result from its minimization or maximization (e.g., maximum water supply, minimum costs, etc.). This is described mathematically by an objective function.
The objective function is subject to the constraints of the problem, which, as mentioned, express the physical, technical, economic, environmental, or regulatory restrictions of the problem. Each one of these constraints is expressed by a function, and all should be met. The variables in all these functions represent the decision parameters (decision variables) under our control to define them (i.e., the solutions of the optimization problem). The optimal solution values will provide the minimum or maximum result of the objective function, having met all the constraints of the problem [37].
For example, an objective function (Z) is set as a goal to maximize (or minimize), under constraints, which are all functions (h) of the decision variables 𝑥1, 𝑥2,𝑥3,…,𝑥𝑛
(1)
The objective function must satisfy a set (i) of constraints (functions y). These are subject to thresholds (e.g., 𝑎𝑖,

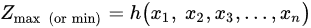
which are known values), expressing the acceptable range of values (2):

(2)
The system’s optimum solution must meet all the constraints and the objective function. This practically provides a useful set-up for several problems, because an objective set, as in Z, can be maximized or minimized, while securing the optimum levels of the other parameters of the system (controlled as 𝑦𝑖 −constraints), all depending on the decision variables [47].
This describes the idea of the general (in this case linear) optimization logic. The different techniques are building on this logic, by following necessary modifications. Depending on the relations of the variables and constraints involved and the mathematical form of the functions used, there are many different optimization techniques, such as non-linear, fuzzy, dynamic, quadratic, or goal programming.
This entry presents a typical problem of integrated WRM, by providing its general formulation, and then its approach from different optimization types offering different representations and answers. The entry is expected to contribute as an educational resource, providing tangible and easily reproducible examples, along with the respective codes.

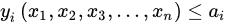
References

  1. Aalami, M.; Nourani, V.; Fazaeli, H. Developing a Surface Water Resources Allocation Model under Risk Conditions with a Multi-Objective Optimization Approach. Water Supply 2020, 20, 1167–1177.
  2. Alamanos, A.; Xenarios, S.; Mylopoulos, N.; Stålnacke, P. Integrated Water Resources Management in Agro-Economy Using Linear Programming: The Case of Lake Karla Basin, Greece. Eur. Water 2017, 60, 41–47.
  3. Zhang, C.-Y.; Oki, T. Water Pricing Reform for Sustainable Water Resources Management in China’s Agricultural Sector. Agric. Water Manag. 2023, 275, 108045.
  4. Dolan, F.; Lamontagne, J.; Link, R.; Hejazi, M.; Reed, P.; Edmonds, J. Evaluating the Economic Impact of Water Scarcity in a Changing World. Nat. Commun. 2021, 12, 1915.
  5. Lukat, E.; Lenschow, A.; Dombrowsky, I.; Meergans, F.; Schütze, N.; Stein, U.; Pahl-Wostl, C. Governance towards Coordination for Water Resources Management: The Effect of Governance Modes. Environ. Sci. Policy 2023, 141, 50–60.
  6. Vörösmarty, C.J.; Hoekstra, A.Y.; Bunn, S.E.; Conway, D.; Gupta, J. Fresh Water Goes Global. Science 2015, 349, 478–479.
  7. Garcia, J.A.; Alamanos, A. A Multi-Objective Optimization Framework for Water Resources Allocation Considering Stakeholder Input. Environ. Sci. Proc. 2023, 25, 32.
  8. Ramadan, E.M.; Abdelwahab, H.F.; Vranayova, Z.; Zelenakova, M.; Negm, A.M. Optimization-Based Proposed Solution for Water Shortage Problems: A Case Study in the Ismailia Canal, East Nile Delta, Egypt. Water 2021, 13, 2481.
  9. Martinsen, G.; Liu, S.; Mo, X.; Bauer-Gottwein, P. Joint Optimization of Water Allocation and Water Quality Management in Haihe River Basin. Sci. Total Environ. 2019, 654, 72–84.
  10. Farrokhzadeh, S.; Hashemi Monfared, S.A.; Azizyan, G.; Sardar Shahraki, A.; Ertsen, M.W.; Abraham, E. Sustainable Water Resources Management in an Arid Area Using a Coupled Optimization-Simulation Modeling. Water 2020, 12, 885.
  11. Musa, A.A. Goal Programming Model for Optimal Water Allocation of Limited Resources under Increasing Demands. Environ. Dev. Sustain. 2021, 23, 5956–5984.
  12. Fu, Q.; Li, T.; Cui, S.; Liu, D.; Lu, X. Agricultural Multi-Water Source Allocation Model Based on Interval Two-Stage Stochastic Robust Programming under Uncertainty. Water Resour. Manag. 2018, 32, 1261–1274.
  13. Ahmad, A.; El-Shafie, A.; Razali, S.F.M.; Mohamad, Z.S. Reservoir Optimization in Water Resources: A Review. Water Resour. Manag. 2014, 28, 3391–3405.
  14. Steele, J.C.; Mahoney, K.; Karovic, O.; Mays, L.W. Heuristic Optimization Model for the Optimal Layout and Pipe Design of Sewer Systems. Water Resour. Manag. 2016, 30, 1605–1620.
  15. Wang, W.; Jia, B.; Simonovic, S.P.; Wu, S.; Fan, Z.; Ren, L. Comparison of Representative Heuristic Algorithms for Multi-Objective Reservoir Optimal Operation. Water Resour. Manag. 2021, 35, 2741–2762.
  16. Stellingwerf, S.; Riddle, E.; Hopson, T.M.; Knievel, J.C.; Brown, B.; Gebremichael, M. Optimizing Precipitation Forecasts for Hydrological Catchments in Ethiopia Using Statistical Bias Correction and Multi-Modeling. Earth Space Sci. 2021, 8, e2019EA000933.
  17. Ibrahim, K.S.M.H.; Huang, Y.F.; Ahmed, A.N.; Koo, C.H.; El-Shafie, A. A Review of the Hybrid Artificial Intelligence and Optimization Modelling of Hydrological Streamflow Forecasting. Alex. Eng. J. 2022, 61, 279–303.
  18. Althoff, D.; Rodrigues, L.N. Goodness-of-Fit Criteria for Hydrological Models: Model Calibration and Performance Assessment. J. Hydrol. 2021, 600, 126674.
  19. Jayasooriya, V.M.; Ng, A.W.M.; Muthukumaran, S.; Perera, C.B.J. Optimization of Green Infrastructure Practices in Industrial Areas for Runoff Management: A Review on Issues, Challenges and Opportunities. Water 2020, 12, 1024.
  20. Alamanos, A.; Papaioannou, G.; Varlas, G.; Markogianni, V.; Papadopoulos, A.; Dimitriou, E. Representation of a Post-Fire Flash-Flood Event Combining Meteorological Simulations, Remote Sensing, and Hydraulic Modeling. Land 2024, 13, 47.
  21. Panahi, M.; Dodangeh, E.; Rezaie, F.; Khosravi, K.; Van Le, H.; Lee, M.-J.; Lee, S.; Thai Pham, B. Flood Spatial Prediction Modeling Using a Hybrid of Meta-Optimization and Support Vector Regression Modeling. CATENA 2021, 199, 105114.
  22. Shishegar, S.; Duchesne, S.; Pelletier, G. Optimization Methods Applied to Stormwater Management Problems: A Review. Urban Water J. 2018, 15, 276–286.
  23. Adedoja, O.S.; Hamam, Y.; Khalaf, B.; Sadiku, R. Towards Development of an Optimization Model to Identify Contamination Source in a Water Distribution Network. Water 2018, 10, 579.
  24. Dai, D.; Alamanos, A.; Cai, W.; Sun, Q.; Ren, L. Assessing Water Sustainability in Northwest China: Analysis of Water Quantity, Water Quality, Socio-Economic Development and Policy Impacts. Sustainability 2023, 15, 11017.
  25. Huang, Y.-K.; Bawa, R.; Mullen, J.; Hoghooghi, N.; Kalin, L.; Dwivedi, P. Designing Watersheds for Integrated Development (DWID): A Stochastic Dynamic Optimization Approach for Understanding Expected Land Use Changes to Meet Potential Water Quality Regulations. Agric. Water Manag. 2022, 271, 107799.
  26. Kryston, A.; Müller, M.F.; Penny, G.; Bolster, D.; Tank, J.L.; Mondal, M.S. Addressing Climate Uncertainty and Incomplete Information in Transboundary River Treaties: A Scenario-Neutral Dimensionality Reduction Approach. J. Hydrol. 2022, 612, 128004.
  27. Englezos, N.; Kartala, X.; Koundouri, P.; Tsionas, M.; Alamanos, A. A Novel HydroEconomic—Econometric Approach for Integrated Transboundary Water Management Under Uncertainty. Environ. Resour. Econ. 2023, 84, 975–1030.
  28. Fu, J.; Zhong, P.-A.; Xu, B.; Zhu, F.; Chen, J.; Li, J. Comparison of Transboundary Water Resources Allocation Models Based on Game Theory and Multi-Objective Optimization. Water 2021, 13, 1421.
  29. Mirzaei-Nodoushan, F.; Bozorg-Haddad, O.; Loáiciga, H.A. Evaluation of Cooperative and Non-Cooperative Game Theoretic Approaches for Water Allocation of Transboundary Rivers. Sci. Rep. 2022, 12, 3991.
  30. Al-Jawad, J.Y.; Alsaffar, H.M.; Bertram, D.; Kalin, R.M. A Comprehensive Optimum Integrated Water Resources Management Approach for Multidisciplinary Water Resources Management Problems. J. Environ. Manag. 2019, 239, 211–224.
  31. Porse, E.; Mika, K.B.; Litvak, E.; Manago, K.F.; Hogue, T.S.; Gold, M.; Pataki, D.E.; Pincetl, S. The Economic Value of Local Water Supplies in Los Angeles. Nat. Sustain. 2018, 1, 289–297.
  32. Alamanos, A.; Koundouri, P.; Papadaki, L.; Pliakou, T.; Toli, E. Water for Tomorrow: A Living Lab on the Creation of the Science-Policy-Stakeholder Interface. Water 2022, 14, 2879.
  33. Koundouri, P.; Halkos, G.; Landis, C.F.M.; Alamanos, A. Ecosystem Services Valuation for Supporting Sustainable Life below Water. Sustain. Earth Rev. 2023, 6, 19.
  34. Sadoff, C.W.; Borgomeo, E.; Uhlenbrook, S. Rethinking Water for SDG 6. Nat. Sustain. 2020, 3, 346–347.
  35. Plagányi, É.; Kenyon, R.; Blamey, L.; Robins, J.; Burford, M.; Pillans, R.; Hutton, T.; Hughes, J.; Kim, S.; Deng, R.A.; et al. Integrated Assessment of River Development on Downstream Marine Fisheries and Ecosystems. Nat. Sustain. 2023, 7, 31–44.
  36. Li, M.; Fu, Q.; Singh, V.P.; Liu, D.; Li, T. Stochastic Multi-Objective Modeling for Optimization of Water-Food-Energy Nexus of Irrigated Agriculture. Adv. Water Resour. 2019, 127, 209–224.
  37. Garcia, J.A.; Alamanos, A. Integrated Modelling Approaches for Sustainable Agri-Economic Growth and Environmental Improvement: Examples from Greece, Canada and Ireland. Land 2022, 11, 1548.
  38. Næss, J.S.; Cavalett, O.; Cherubini, F. The Land–Energy–Water Nexus of Global Bioenergy Potentials from Abandoned Cropland. Nat. Sustain. 2021, 4, 525–536.
  39. Hashmi, A.H.A.; Ahmed, S.A.S.; Hassan, I.H.I. Optimizing Pakistan’s Water Economy Using Hydro-Economic Modeling: Optimizing Pakistan’s Water Economy Using Hydro-Economic Modeling. J. Bus. Econ. 2019, 11, 111–124.
  40. Alamanos, A.; Koundouri, P. Emerging Challenges and the Future of Water Resources Management. In Hydrolink 2022/10. Madrid: International Association for Hydro-Environment Engineering and Research (IAHR); Henry: Karlsruhe, Germany, 2022; Available online: https://hdl.handle.net/20.500.11970/110818 (accessed on 8 December 2023).
  41. Pascual, A.; Giardina, C.P.; Povak, N.A.; Hessburg, P.F.; Heider, C.; Salminen, E.; Asner, G.P. Optimizing Invasive Species Management Using Mathematical Programming to Support Stewardship of Water and Carbon-Based Ecosystem Services. J. Environ. Manag. 2022, 301, 113803.
  42. Abadie, L.M.; Markandya, A.; Neumann, M.B. Accounting for Economic Factors in Socio-Hydrology: Optimization under Uncertainty and Climate Change. Water 2019, 11, 2073.
  43. Angeli, A.; Karkani, E.; Alamanos, A.; Xenarios, S.; Mylopoulos, N. Hydrological, Socioeconomic, Engineering and Water Quality Modeling Aspects for Evaluating Water Security: Experience from Greek Rural Watersheds. In Proceedings of the EGU General Assembly, Online, 4–8 May 2020; EGU: Vienna, Austria, 2020.
  44. Eisenstein, M. Natural Solutions for Agricultural Productivity. Nature 2020, 588, S58–S59.
  45. Puy, A.; Massimi, M.; Lankford, B.; Saltelli, A. Irrigation Modelling Needs Better Epistemology. Nat. Rev. Earth Environ. 2023, 4, 427–428.
  46. Allen, D.C.; Datry, T.; Boersma, K.S.; Bogan, M.T.; Boulton, A.J.; Bruno, D.; Busch, M.H.; Costigan, K.H.; Dodds, W.K.; Fritz, K.M.; et al. River Ecosystem Conceptual Models and Non-Perennial Rivers: A Critical Review. WIREs Water 2020, 7, e1473.
  47. Dantzig, G.B.; Thapa, M.N. (Eds.) The Linear Programming Problem. In Linear Programming: 1: Introduction; Springer Series in Operations Research and Financial Engineering; Springer: New York, NY, USA, 1997; pp. 1–33. ISBN 978-0-387-22633-0.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Engineering, Civil; Environmental Sciences
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Angelos Alamanos
,
Jorge Andres Garcia
View Times: 81
Online Date: 08 Feb 2024
Table of Contents
    1000/1000
    Hot Most Recent
    Feedback