
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Souhail Mssassi | -- | 2473 | 2024-01-25 18:27:40 | | | |
| 2 | Fanny Huang | + 8 word(s) | 2481 | 2024-01-30 08:39:42 | | | | |
| 3 | Fanny Huang | -43 word(s) | 2438 | 2024-01-31 09:57:23 | | |
Video Upload Options
Blockchain technology has permeated various sectors and has been lauded for its potential to instill immutability, transparency, and decentralization in systems, thereby revolutionizing traditional systems. At the core of these decentralized networks, nodes are imperative for executing and validating transactions, thereby safeguarding the integrity of the blockchain. Within this ecosystem, nodes, particularly those executing transactions encompassing native currency transfers and function executions, are pivotal yet often lack adequate incentives, in contrast to mining nodes.
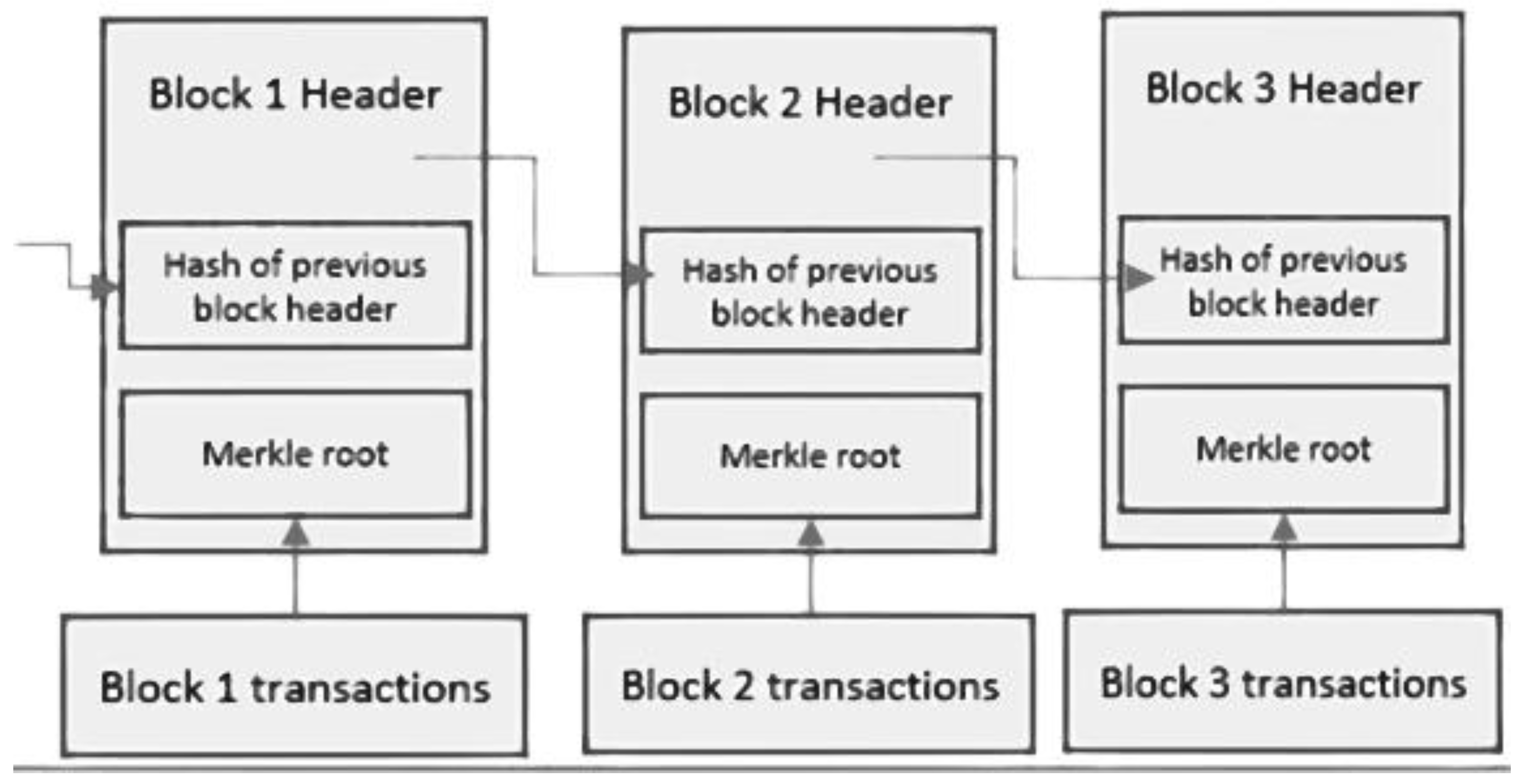
1. Blocks
- −
-
The term “magic number” refers to a numerical figure encompassing distinct characteristics and serving as an identifier for a single block inside the network.
- −
-
The block size parameter establishes a predetermined restriction on the size of a block, which restricts the amount of data that may be inputted.
- −
-
The block header is a component that contains pertinent information on the block.
- −
-
The transaction counter is a numerical value that indicates the total number of transactions in a given block.
- −
-
Transactions refer to a comprehensive batch of all recorded transactions in a particular block [1].
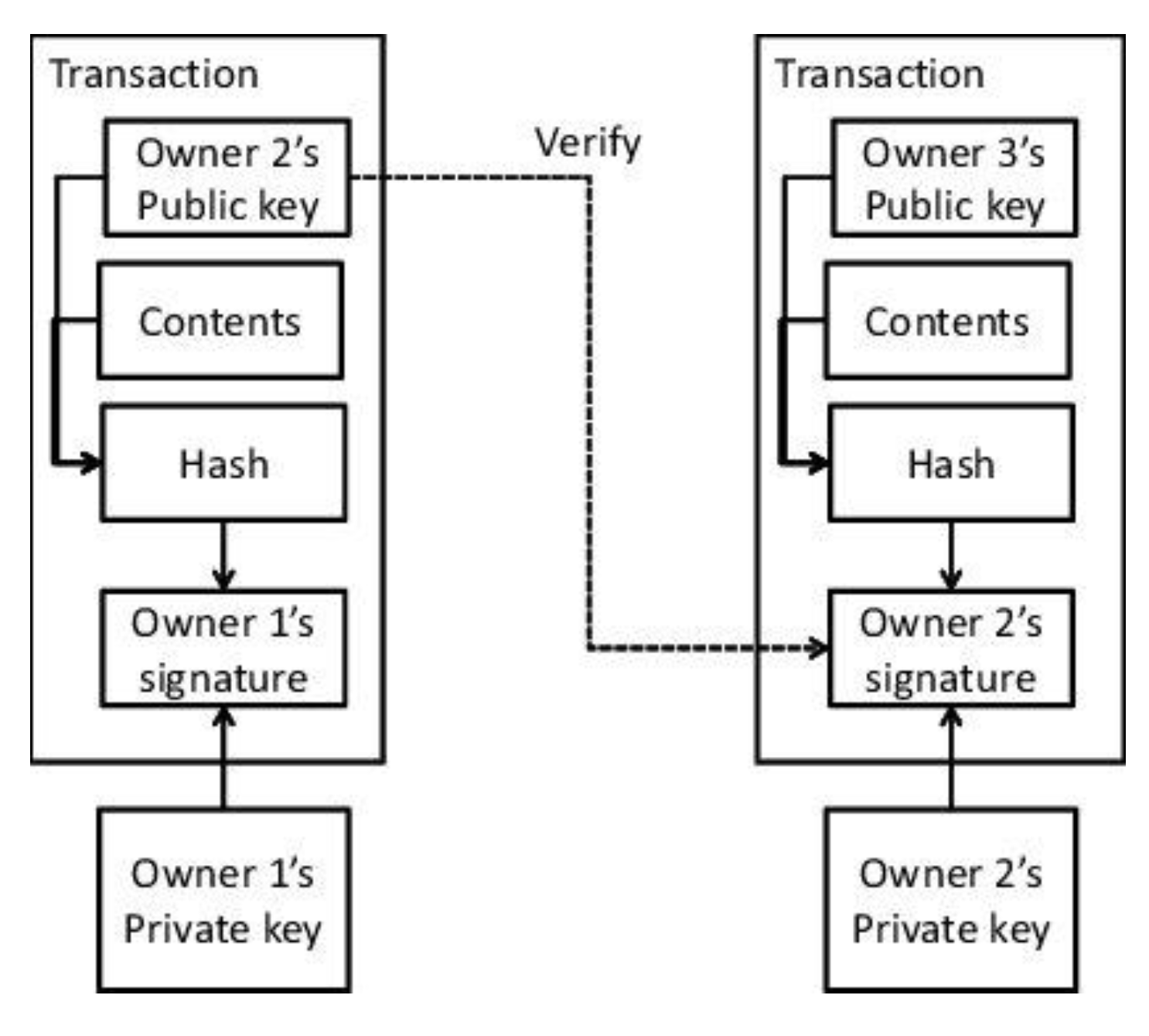
2. Transactions
3. Nodes
| Aspect | Transaction-Executing Nodes | Mining Nodes |
|---|---|---|
| Purpose | Validate and relay transactions across the network. | Add new blocks to the blockchain. |
| Primary Responsibility | Ensure transactions comply with network rules. | Collect, verify, and process transactions into blocks. |
| Reward System | Do not typically receive cryptocurrency rewards. | Receive rewards in the form of minted cryptocurrency. |
| Hardware Requirements | Do not require significant computational power. | Requires high computational power. |
| Storage | It may or may not store the entire blockchain history. | Store blockchain as the whole history and validation transactions. |
| Incentive | Maintain network integrity for their applications. | Monetary rewards for adding successful blocks. |
-
Nodes play a crucial role in the validation process of determining the legitimacy of a block of transactions because they have the authority to accept or reject it.
-
The nodes are responsible for preserving and retaining transaction blocks, including the entire transaction record in the blockchain.
-
The transaction history is distributed and propagated by nodes to other nodes, which may require synchronization with the blockchain [1].
4. Game Theory
5. Nash Equilibrium
6. Graph Modeling of Blockchain Nodes and Researchers' Game Framework
Blockchain networks consist of several nodes engaging in interactions and reaching choices guided by self-interests. In the initial phase of developing researchers' framework, it is essential to construct a mathematical model to facilitate a deeper understanding of the interactions among nodes within the blockchain network. Researchers chose to represent the network using a graph-based model owing to graphs’ versatile properties and structural intricacies. Specifically, researchers opted for an undirected graph to illustrate node communication dynamics effectively. Furthermore, the representation of the graph in a matrix form simplifies its depiction and enhances its integration into researchers' algorithmic constructs. Subsequent stages involve incorporating this matrix into the strategic game, meticulously formalized in the forthcoming chapter. This integration enables nodes to make informed decisions in each round and adjust their trust matrices accordingly. The final step involves the implementation of an incentive mechanism designed to reward nodes proportionally based on their honest contributions and overall participation in the network. Figure 3 provides a high-level overview of this entire process, illustrating the key stages and how they interconnect within researchers' framework.
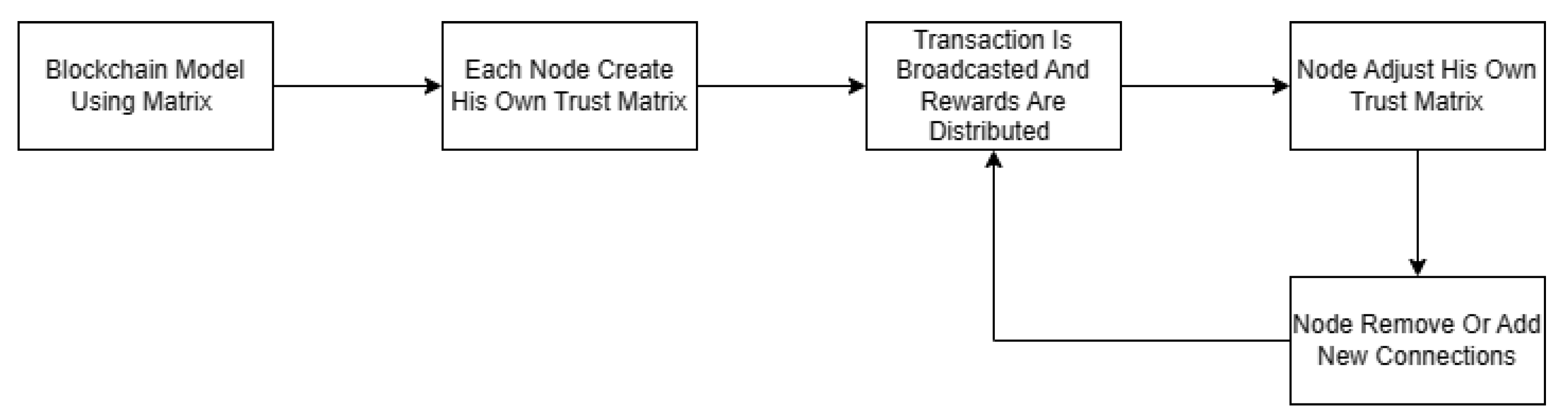
Figure 3. High-level overview of researchers' process.
7. Game Framework and Rules
In the initial phase of researchers' research, researchers focused on conceptualizing interactions within a blockchain network using graph theory and matrix representations. This part aims to construct a strategic game, facilitating nodes to adjust their trust matrix and make strategic decisions over successive rounds. These decisions include creating or removing connections with other nodes based on evolving strategies. Researchers begin by defining the critical elements of the framework as follows.
▪ Set of Players: This is represented by a finite set of nodes within the graph, denoted as 𝑁={1,2,…,n}, where each node is a player in the game. These players can exhibit malicious or honest behaviors depending on their chosen strategies. To capture the dynamic nature of the network and align with real-world scenarios, a node is permitted to switch strategies across rounds, thus enabling both cooperative and non-cooperative behaviors.
▪ Actions/Strategies: Nodes have two fundamental types of actions. The first relates to handling transactions or messages, where a node decides to either forward it to the next node or refrain from doing so, essentially choosing to cooperate. This can be represented by a binary sequence, such as {00011…00}. For simplicity, researchers initially assume that a node applies the same action uniformly across all nodes, although the model retains the flexibility to account for varying actions in future iterations. The second action concerns modifying relationships with other nodes, influenced by their strategy and the trust matrix. This could entail removing connections with nodes that fall below a specific reputation score, as determined by the trust matrix.
▪ Payoffs: Each node’s actions result in a reward or a penalty. Actively participating in transaction broadcasting yields rewards proportionate to the node’s contribution to the network’s connectivity and transaction throughput. In contrast, non-cooperative behavior reduces the node’s reputation, potentially leading to isolation within the network. For this process to be fair, a node will be rewarded based on his weight and contribution to the network, meaning that a node that broadcasted to three nodes will not be rewarded the same as one that broadcasted to ten nodes; having this logic will incentivize nodes to prefer to be hubs in the network. The Reward System chapter provides a detailed exposition of this mechanism.
▪ Order of Play: The first player in each round is determined by the initiator of the transaction, essentially chosen using a pseudo-random process based on transaction initiation. The selected node then propagates the transaction to other nodes, akin to a token being passed in a ring topology.
The game possesses several distinct characteristics:
▪ Cooperative Nature: The framework views nodes as components of potential coalitions, with an ideal scenario being a single unified coalition. Represented as (𝑁,𝑣), the game promotes common interests by focusing on a network’s well-being and security. The power set 2𝑛 encapsulates all possible coalitions, for example, for a graph of three nodes. At first sight, it appears that the most optimal strategy for a node is to be alone in its coalition. However, because the game is repetitive, acting with this strategy may be better because it does not encourage nodes to participate in the group’s gain. The design incentivizes stable and fair coalitions, where no subset of players is incentivized to form a smaller coalition, and each player’s payoff is proportional to their contribution.
▪ Repetitive Game Structure: Denoted as 𝐺𝑇 The game is repetitive, with players selecting strategies at each stage of the game iteration. The cumulative payoff is the sum of the rewards obtained across all stages, and strategies are adapted based on the history of the play, allowing dynamic responses to the outcomes of previous rounds.
▪ Non-Zero-Sum Nature: The game is designed as a non-zero-sum game. If 𝑢𝑖(𝑠𝑖) denotes the payoff for choosing a strategy, then no combination of strategies results in a total payoff sum of zero.
References
- Nakamoto, S.; Bitcoin: A Peer-to-Peer Electronic Cash System. December 2008. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 21 August 2023).
- Antonopoulos, A.M. Mastering Bitcoin: Unlocking Digital Crypto-Currencies; O’Reilly Media, Inc.: Newton, MA, USA, 2014.
- Mingxiao, D.; Xiaofeng, M.; Zhe, Z.; Xiangwei, W.; Qijun, C. A review on consensus algorithm of blockchain. In Proceedings of the 2017 IEEE International Conference on Systems, and Cybernetics (SMC), Man, Banff, AB, Canada, 5–8 October 2017; pp. 2567–2572.
- Osborne, M.J. An Introduction to Game Theory; Oxford University Press: Oxford, UK, 2004; Volume 3.
- Fudenberg, D.; Tirole, J. Game Theory; MIT press: Cambridge, MA, USA, 1991.
- Liu, Z.; Luong, N.C.; Wang, W.; Niyato, D.; Wang, P.; Liang, Y.-C.; Kim, D.I. A survey on applications of game theory in blockchain. arXiv 2019, arXiv:1902.10865.
- Kreps, D.M. Nash equilibrium. In Game Theory; Springer: Berlin/Heidelberg, Germany, 1989; pp. 167–177.




