Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Yiyo Kuo
 -- 2006 2024-01-16 10:15:32 |
2 layout & references
Sirius Huang
 Meta information modification 2006 2024-01-17 01:59:58 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Kuo, Y.; Chen, S.; Yang, T.; Hsu, W. U-Shaped Conveyor Assembly Line Balancing Problem. Encyclopedia. Available online: https://encyclopedia.pub/entry/53880 (accessed on 17 May 2024).
Kuo Y, Chen S, Yang T, Hsu W. U-Shaped Conveyor Assembly Line Balancing Problem. Encyclopedia. Available at: https://encyclopedia.pub/entry/53880. Accessed May 17, 2024.
Kuo, Yiyo, Ssu-Han Chen, Taho Yang, Wei-Chen Hsu. "U-Shaped Conveyor Assembly Line Balancing Problem" Encyclopedia, https://encyclopedia.pub/entry/53880 (accessed May 17, 2024).
Kuo, Y., Chen, S., Yang, T., & Hsu, W. (2024, January 16). U-Shaped Conveyor Assembly Line Balancing Problem. In Encyclopedia. https://encyclopedia.pub/entry/53880
Kuo, Yiyo, et al. "U-Shaped Conveyor Assembly Line Balancing Problem." Encyclopedia. Web. 16 January, 2024.
U-Shaped Conveyor Assembly Line Balancing Problem
Edit
This entry is adapted from the peer-reviewed paper 10.3390/app13063702

Conveyors are used when material is to be moved frequently between specific points. Line balancing involves allocating an equal amount of work to each workstation along the line. The fundamental line balancing problem is to assign a set of tasks to an ordered set of workstations, so that the precedence relationships are satisfied and some measure of performance is optimized.

conveyor line balancing simulated annealing U-shaped assembly line walking times

1. Introduction

Conveyors are used when material is to be moved frequently between specific points [1]. When there is sufficient throughput between fixed points, the use of conveyors is suggested [2] for high-efficiency transport over short and medium distances [3][4]. Conveyors are also used in assembly line systems, generally in two different configurations. In the first, items are transported between machines by conveyors. Once the items arrive at a machine, the operators move them off the conveyor for assembling and then put them back on the conveyor to move them to subsequent machines. In this case, the positions of operators are fixed when assembling items. In the second case, the items may be large or not easily handled, and are not easily moved. The items are fixed to the moving conveyor, and operators execute their assembly tasks moving beside the conveyor as they work. After finishing all their assembly tasks, the operators walk back to their original locations and execute the assembly tasks for the next item.
Line balancing involves allocating an equal amount of work to each workstation along the line [5]. The fundamental line balancing problem is to assign a set of tasks to an ordered set of workstations, so that the precedence relationships are satisfied and some measure of performance is optimized [6]. For the second case of conveyor assembly lines, operators have to move along the conveyors while executing assembly tasks and walk back to their original locations after finishing the assembly tasks assigned to them. Walking time between assembly tasks should be taken into consideration when balancing such assembly lines.
In traditional straight assembly lines, the walking times are proportional to the corresponding assembly times and can be integrated into assembly time, because the operators walk back to their original locations beside the conveyor and the times depend on the distance that the conveyor moves while the operators execute the assembly tasks. A U-shaped conveyor assembly line, however, is divided into two sub-lines: the entrance sub-line and exit sub-line. An operator may be able to execute assembly tasks on both sub-lines within the same work cycle [7], and the estimation of walking times between assembly tasks for each operator is more complicated. For example, in Figure 1, there are 7 assembly tasks. The assembly sequence is 1, 2, 3, 4, 5, 6, and 7, so that no precedence relationships are violated. Tasks 1 and 7 are assigned to Operator 1, Tasks 2 and 6 are assigned to Operator 2, and Tasks 3, 4 and 5 are assigned to Operator 3. According to the sequence and the corresponding assembly times, a, b, c, d, e, f, g, h indicate the starting and completing points of tasks. The dotted lines with arrows are the walking paths between assembly tasks. For example, Operator 1, executes assembly Task 1 from point a to point b, taking the assembly time of Task 1, and then walks to point g without executing assembly tasks. He/she then executes assembly Task 7 from point g to point h, taking the time of Task 7, and then walks back to point a without executing assembly tasks.
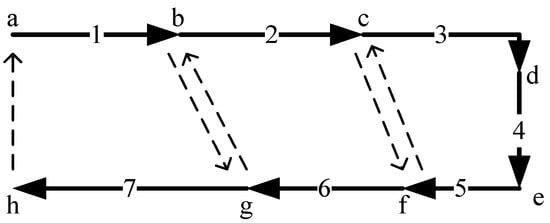
Applsci 13 03702 g001 550
Figure 1. An example of walking paths in a U-shaped conveyor assembly line.
According to the example shown in Figure 1, the time spent walking between assembly tasks depends on the sequence of tasks, the assembly time of tasks, the allocation of tasks to workstations and the configuration of the U-shaped conveyor assembly line. Therefore, it is not easy to take walking times into consideration when balancing the second case of U-shaped conveyor assembly lines where the items are fixed to the conveyor.
There are four types of assembly line balancing problem [8]. Type 1 aims to minimize the number of stations for a given cycle time. Type 2 aims to minimize the cycle time for a given number of workstations. Type E aims to maximize the efficiency with a specified cycle time or number of workstations. Additionally, Type F aims to find a feasible design for a given cycle time and number of workstations. 

2. Problems that Relate to Balancing Conveyor Assembly Lines

Research that deals with problems that relate to balancing conveyor assembly lines mainly focuses on traditional straight assembly lines. Xiaobo and Ohno [9] dealt with the concept in the Toyota production system, which permits operators to stop the conveyor whenever they fail to complete the operations within their work stations in a mixed-model assembly line. They took walking time into consideration to formulate a sequencing problem and then proposed a heuristic algorithm to minimize total conveyor stoppage time. Zhao et al. [10] described a balancing problem for mixed-model assembly lines with a paced moving conveyor. All operators can only execute their assembly tasks within a boundary. Operators execute their assembly tasks as the items move on the conveyor, then walk back to the position of the next product that the assembly tasks assign to them. If assembly tasks cannot be completed within the boundary, overload time occurs. When overloads occur, the unfinished assembly task has to be completed offline or the conveyor must be stopped temporarily. A heuristic is proposed to minimize the total overload time. Mendes et al. [11] described a mixed-model PC camera assembly line balancing problem. Firstly, a heuristic procedure previously developed based on the SA meta-heuristic, is used to derive line configurations with a minimum number of workstations and a smooth workload balance between and within the workstations. Then, the solutions provided by the heuristic procedure are used as an input to discrete event simulation models in order to test the robustness of these solutions. Kim and Jeong [12] proposed a heuristic procedure for optimizing the input sequence of product models with sequence-dependent setup times in a mixed-model assembly line using a conveyor system. All operators are forced to complete their operations within their predetermined work zone. The goal is to minimize the total of unfinished work within their work zone. Experimental results show that the heuristic procedure provides reasonably good solutions with low computational costs. Kim et al. [13] presented a mixed-integer programming model and a genetic algorithm (GA) to solve the minimum cycle time with a given number of workstations for two-sided assembly line balancing problems in which different assembly tasks on the same product item can be performed in parallel on both sides of the conveyor line. The experimental results show that the proposed GA outperforms the heuristic and the existing GA. Defersha and Mohebalizadehgashti [14] proposed a mixed-integer linear programming mathematical model to optimize balancing and sequencing problems for a continuously moving conveyor. They developed a multi-phased linear programming embedded GA to minimize the length and number of workstations, costs of workstations and task duplication. Numerical examples were presented to illustrate the model and the computational efficiency of the developed hybrid genetic algorithm. Based on the results obtained, the proposed algorithm outperformed the branch and bound algorithm in finding acceptable solutions. Pearce et al. [15] presented a complex line balancing problem based on a real conveyor assembly environment with task-to-task relationships, station characteristics limiting assignment, and parallel worker zoning interactions. A heuristic, combining rank-position-weighting, last-fit-improvement and iterative blocking schemes, and an integer programming that can manage multiple constraint types simultaneously were developed. Experimental results indicate that the integer programming model provides a viable solution method for those industries with access to commercial solvers.
Research dealing with U-shaped conveyor assembly line balancing problems is rare. Hwang et al. [16] proposed a multi-objective genetic algorithm to solve the U-shaped conveyor assembly line balancing problem. The performance criteria considered were the number of workstations (equal to the number of operators) and the variation of workload. Hwang and Katayama [17] proposed a new evolutionary approach to deal with workload balancing problems in mixed-model U-shaped conveyor assembly lines. The same task on different products is assumed to take the same time. The performance criteria were the same as Hwang et al. [16]. A case study was examined as a validity check in collaboration with a manufacturing company. Li et al. [18] dealt with U-shaped conveyor assembly line balancing problems in which task times are uncertain and corresponding historical information is not available due to technology changes, environmental changes, or the effect of learning on the part of operators. An uncertain programming model that minimizes the number of workstations was proposed first. Then, the uncertain model was transferred into a deterministic model to reduce computational effort. Finally, an algorithm was developed based on a branch and bound memory algorithm to find the optimal solution. Although Hwang et al. [16], Hwang et al. [17] and Li et al. [18] dealt with U-shaped conveyor assembly line balancing problems, they ignored walking times.
U-shaped assembly line balancing problems are similar to the proposed problem, but most of them also ignored walking times. In recent years, Zhang et al. [19] addressed the Type 2 U-shaped robotic assembly line balancing problem, in which the objectives are to minimize the cycle time and energy consumption simultaneously. The Pareto artificial bee colony algorithm (PABC) is extended to tackle this problem. Zhang et al. [20] applied an occupational repetitive action method to calculate the ergonomic risk value. A worker assignment and balancing problem of Type 2 for a U-shaped assembly line to minimize cycle time and ergonomic risks was then formulated. A multi-objective restarted iterative Pareto greedy algorithm is proposed to tackle this problem. Chantarasamai and Lasunon [21] described a differential evolution algorithm for solving U-shaped assembly line balancing problems. The objective is to minimize cycle time for a just-in-time production line that produces a single product with a certain number of workstations. Pinarbasi [22] considered a U-shaped assembly line balancing problem with stochastic assembly times. Two new chance-constrained non-linear models are proposed. The results are compared with the results of modified ant colony optimization and a piecewise-linear programming model. The study shows that the proposed two models are more effective and successful in solving stochastic U-shaped assembly line balancing problems. Chutima and Khotsaenlee [23] dealt with the parallel adjacent U-shaped assembly line balancing problem. Operators and robots are assigned to execute assembly tasks in the same work cycle. Assembly tasks located in two adjacent U-shaped assembly lines can assigned to the same operator or robot. Moreover, both fully able and disabled operators are considered. A mathematical model with five objective functions is developed. Then, non-dominated sorting teaching-learning-based optimization is proposed to solve the proposed problems. Khorram et al. [24] aim to optimize activity-to-station and operator-to-station decisions in a U-shaped assembly line balancing problem. Criteria such as equipment cost, number of stations and quality of activity performance are considered simultaneously. As an approach to solving the problem, classical simulated annealing (SA), variable neighborhood search (VNS), and a genetic algorithm (GA) were adopted for optimization.
Very few studies consider walking times in U-shaped assembly line balancing problems. Ohno and Nakade [25] considered walking times and formulated the optimal operator allocation problem to minimize the overall cycle time and discussed the two operator allocation problem as a special case. Nakade and Ohno [26] proposed an algorithm for finding an optimal allocation of operators to machines that minimizes the cycle time for the minimum number of operators. Shewchuk [27] proposed a mathematical model that takes walking time into account, with operators following circular paths and walking around other operators. A heuristic algorithm was developed to optimize the allocation of operators. Although Ohno and Nakade [25], Nakade and Ohno [26] and Shewchuk [27] take walking times into consideration, the sequence of tasks is fixed and unchangeable. Kuo et al. [28] proposed an integer programming formulation which takes both precedence relationships of tasks and walking times between locations into consideration. The sequence of tasks and allocation of operators are optimized simultaneously. The four studies that consider walking times, described above, assume that the locations of items are fixed, and a conveyor is not used to move the assembled products. If operators have to execute another consecutive assembly task, they have to walk to the next location. 

References

  1. Tompkings, J.A.; White, J.A.; Bozer, Y.A.; Tanchoco, J.M.A. Facilities Planning, 4th ed.; John Wiliey and Sons, INC.: Hoboken, NJ, USA, 2010.
  2. Arnold, J.R.T.; Chapman, S.N. Introduction to Materials Management, 5th ed.; Pearson Prentice Hall: Columbus, OH, USA, 2004.
  3. Zhang, S.; Xia, X. Optimal control of operation efficiency of belt conveyor systems. Appl. Energy 2010, 87, 1929–1937.
  4. Masaki, M.S.; Zhang, L.; Xia, X. A comparative study on the cost-effective belt conveyors for bulk material handling. Energy Procedia 2017, 142, 2754–2760.
  5. Ponnambalam, S.G.; Aravindan, P.; Mogileeswar Naidu, G. A comparative evaluation of assembly line balancing heuristics. Int. J. Adv. Manuf. Technol. 1999, 15, 577–586.
  6. Ghosh, S.; Gagnon, R.J. A comprehensive literature review and analysis of the design, balancing and scheduling of assembly lines. Int. J. Prod. Res. 1989, 27, 637–670.
  7. Li, M.; Tang, Q.; Zheng, Q.; Xia, X.; Floudas, C.A. Rules-based heuristic approach for the U-shaped assembly line balancing problem. Appl. Math. Model. 2017, 48, 423–439.
  8. Scholl, A.; Becker, C. State-of-the-art exact and heuristic solution procedures for simple assembly line balancing. Eur. J. Oper. Res. 2006, 168, 666–693.
  9. Xiaobo, Z.; Ohno, K. Properties of a sequencing problem for a mixed model assembly line with conveyor stoppages. Eur. J. Oper. Res. 2000, 124, 560–570.
  10. Zhao, X.; Ohno, K.; Lau, H.S. A balancing problem for mixed model assembly lines with a paced moving conveyor. Nav. Res. Logist. 2004, 51, 446–464.
  11. Mendes, A.R.; Ramos, A.L.; Simaria, A.S.; Vilarinho, P.M. Combining heuristic procedures and simulation models for balancing a PC camera assembly line. Comput. Ind. Eng. 2005, 49, 413–431.
  12. Kim, S.; Jeong, B. Product sequencing problem in Mixed-Model Assembly Line to minimize unfinished works. Comput. Ind. Eng. 2007, 53, 206–214.
  13. Kim, Y.K.; Song, W.S.; Kim, J.H. A mathematical model and a genetic algorithm for two-sided assembly line balancing. Comput. Oper. Res. 2009, 36, 853–865.
  14. Defersha, F.M.; Mohebalizadehgashti, F. Simultaneous balancing, sequencing, and workstation planning for a mixed model manual assembly line using hybrid genetic algorithm. Comput. Ind. Eng. 2018, 119, 370–387.
  15. Pearce, B.W.; Antani, K.; Mears, L.; Funk, K.; Mayorga, M.E.; Kurz, M.E. An effective integer program for a general assembly line balancing problem with parallel workers and additional assignment restrictions. J. Manuf. Syst. 2019, 50, 180–192.
  16. Hwang, R.K.; Katayama, H.; Gen, M. U-shaped assembly line balancing problem with genetic algorithm. Int. J. Prod. Res. 2008, 46, 4637–4649.
  17. Hwang, R.K.; Katayama, H. A multi-decision genetic approach for workload balancing of mixed-model U-shaped assembly line systems. Int. J. Prod. Res. 2009, 47, 3797–3822.
  18. Li, Y.; Hu, X.; Tang, X.; Kucukkoc, I. Type-1 U-shaped Assembly Line Balancing under uncertain task time. IFAC Pap. 2019, 52, 992–997.
  19. Zhang, Z.; Tang, Q.; Li, Z.; Zhang, L. Modelling and optimization of energy-efficient U-shaped robotic assembly line balancing problems. Int. J. Prod. Res. 2019, 57, 5520–5537.
  20. Zhang, Z.; Tang, Q.; Ruiz, R.; Zhang, L. Ergonomic risk and cycle time minimization for the U-shaped worker assignment assembly line balancing problem: A multi-objective approach. Comput. Oper. Res. 2020, 118, 104905.
  21. Chantarasamai, K.; Lasunon, O.U. Modified differential evolution algorithm for U-shaped assembly line balancing type 2. Int. J. Intell. Eng. Syst. 2021, 14, 452–462.
  22. Pınarbasi, M. New chance-constrained models for U-type stochastic assembly line balancing problem. Soft Comput. 2021, 25, 9559–9573.
  23. Chutima, P.; Khotsaenlee, A. Multi-objective parallel adjacent U-shaped assembly line balancing collaborated by robots and normal and disabled workers. Comput. Oper. Res. 2022, 143, 105775.
  24. Khorram, M.; Eghtesadifard, M.; Niroomand, S. Hybrid meta-heuristic algorithms for U-shaped assembly line balancing problem with equipment and worker allocations. Soft Comput. 2022, 26, 2241–2258.
  25. Ohno, K.; Nakade, K. Analysis and optimization of a U-shaped production line. J. Oper. Res. Soc. Jpn. 1997, 40, 90–104.
  26. Nakade, K.; Ohno, K. An optimal walker allocation problem for a U-shaped production line. Int. J. Prod. Econ. 1999, 60–61, 353–358.
  27. Shewchuk, J.P. Worker allocation in lean U-shaped production lines. Int. J. Prod. Res. 2008, 46, 3485–3502.
  28. Kuo, Y.; Yang, T.; Huang, T.L. Optimizing U-shaped production line balancing problem with exchangeable task locations and walking times. Appl. Sci. 2022, 12, 3375.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Mathematics, Applied
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Yiyo Kuo
,
Ssu-Han Chen
,
Taho Yang
,
Wei-Chen Hsu
View Times: 113
Revisions: 2 times (View History)
Update Date: 17 Jan 2024
Table of Contents
    1000/1000
    Hot Most Recent
    Feedback