Your browser does not fully support modern features. Please upgrade for a smoother experience.

Submitted Successfully!
Thank you for your contribution! You can also upload a video entry or images related to this topic.
For video creation, please contact our Academic Video Service.
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Soon Seok Kim | -- | 2214 | 2023-07-25 12:45:55 | | | |
| 2 | Camila Xu | Meta information modification | 2214 | 2023-07-26 03:18:20 | | |
Video Upload Options
We provide professional Academic Video Service to translate complex research into visually appealing presentations. Would you like to try it?
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Kim, S. Anonymizing Transaction Data with Set Values. Encyclopedia. Available online: https://encyclopedia.pub/entry/47246 (accessed on 08 February 2026).
Kim S. Anonymizing Transaction Data with Set Values. Encyclopedia. Available at: https://encyclopedia.pub/entry/47246. Accessed February 08, 2026.
Kim, Soon-Seok. "Anonymizing Transaction Data with Set Values" Encyclopedia, https://encyclopedia.pub/entry/47246 (accessed February 08, 2026).
Kim, S. (2023, July 25). Anonymizing Transaction Data with Set Values. In Encyclopedia. https://encyclopedia.pub/entry/47246
Kim, Soon-Seok. "Anonymizing Transaction Data with Set Values." Encyclopedia. Web. 25 July, 2023.
Copy Citation
The definition of anonymity emphasizes the fact that the attacker can identify a person based on some of the sensitive set values about which the attacker has prior knowledge of in the set value data.
anonymization
transaction data
set value
de-identification
1. Introduction
In 2008, Manolis Terrovitis of Nikos Mamoulis [1][2][3] observed that when an attacker had partial knowledge about the subsets of items purchased by an individual, the direct disclosure of Database D would make public the identity of a person related to a certain transaction. For instance, Bob purchased a set of items including coffee, bread, brie cheese, diapers, milk, tea, scissors, and light bulbs at a supermarket on a certain day. Bob’s neighbor Jim was on the same bus as him and saw some of his items (e.g., brie cheese, scissors, and light bulbs) in the shopping bag. Bob would not want Jim to find out the rest of the items he purchased. If the supermarket decided to make public the transaction information with only one transaction including brie cheese, scissors, and light bulbs, Jim could immediately infer that this transaction was made by Bob and find out the entire content of his shopping bag. A proposed solution to this issue was called km-anonymity (Global Generalization). When the attacker has maximum knowledge of the maximum number of items ‘m’ in a certain transaction (in a set of transaction records), the attacker will be prevented from distinguishing the number of transaction sets and transactions ‘k’ in Database D. Likewise, Database D, for the set of items under ‘m’, should include minimum ‘k’ number of transactions, including the set. In this example, Jim cannot distinguish Bob’s transaction in the minimum five transaction sets in D that has 53-anonymity. This definition of anonymity emphasizes the fact that the attacker can identify a person based on some of the sensitive set values about which the attacker has prior knowledge of in the set value data. In some cases, however, it would be impossible for the attacker to determine in advance the threshold of the number of items in transactions of which he or she has prior knowledge. In such a case, it is impossible to select a safe value for m itself. Another example is when certain transactions can be excluded that are not connected to an individual based on some items of a set. The attacker, for instance, may have knowledge of certain items purchased only by people 65 years or older and other items purchased only by people living in a certain area. In such a case, km-anonymity cannot protect individuals from attacks. Puri et al. [4] used a bottom-up strategy based on global generalization to further strengthen km-anonymity. Vartika et al. [5] proposed a (k, m, t)-anonymity algorithm to effectively prevent skewness attacks and disclosure of identity and attributes on transactions. This algorithm clusters k records of combinations of m items. Then, it was constructed by adding a threshold value t for the distance between the distributions of sensitive attributes within the cluster. Andrew et al. [6] proposed a greedy heuristic protection method against an attack, in which elected representatives in communication with data owners and collectors cooperate and collude, based on the above clustering.
Y. Xu et al. [7][8] proposed the (h, k, p)-consistency as a more specific privacy criterion to anonymize set value data. The (h, k, p)-consistency guarantees that a database containing insensitive p item combinations includes a minimum k number of transactions, and that a maximum h% of transactions include some sensitive items. In other words, this approach models the attacker’s prior knowledge of the parameter p and provides the flexibility of anonymization. km-anonymity concerns special cases of h = 100% and p = m, but this method has the problem of high rates of information loss by employing suppression technology for all the items whose distribution is relatively small, in order to reinforce safety. The next chapter offers examples of such cases. In addition, this model is based on the assumption that it cannot be directly applied to issues not based on the assumption because there are categories of quasi-identifiers and sensitive information. Cao et al. [9] proposed a ρ-uncertainty model to provide privacy protection from attribute disclosure as opposed to (h, k, p)-consistency. The ρ-uncertainty model limits the likelihood that an individual correlates with a sensitive item that is less than a threshold ρ. Related anonymization techniques include the global generalization-based algorithm and suppression-based algorithm in [9], partial suppression through divide and conquer proposed by Jia et al. [10], and the personalized ρm- and (ε, σ)-ρm-uncertainty models [11] have also been proposed.
Yeye He and Jeffrey F. Naughton [12] proposed the k-anonymity technique—or the “Local Generalization” technique—to solve the issues raised in [1][3][7][8] above. Based on the “Local Recording” technique defined by the anonymization categorization proposed by [13], this technique provides a definition that k-anonymity will be satisfied if each transaction is the same as a minimum k − 1 number of other transactions. Unlike km-anonymity, which only protects personal privacy when the attackers have knowledge of items under the number of m, k-anonymity requires no limits to the number of items that the attacker may have knowledge of in the absence of the parameter m. In general, a lower m of km-anonymity inevitably means weaker privacy provided by km-anonymity. k-anonymity, however, guarantees privacy more strongly than km-anonymity. While km-anonymity takes a bottom-up approach, k-anonymity uses a top-down greedy partitioning (tree separation) algorithm and, thus, takes much less time to perform CPU functions than the existing techniques [1][2][3][7][8]. Since k-anonymity takes a top-down partition approach, it has the weakness of huge information loss by applying the same generalization to the domains partitioned under the generalization tree structure of each transaction item, especially the items of unique values. Junqiang Liu and Ke Wang [14] pointed out this disadvantage of k-anonymity and proposed a new technique called the HgHs (Heuristic generalization with Heuristic suppression) algorithm. This technique finds optical heuristic cutting (tree separation) points in a generalization tree structure and applies generalization and suppression techniques to them. Although it guarantees less information loss than the k-anonymity technique, it focuses on CPU performance. As a different approach from the proposed method, Loukides and Gkoulalas-Divanis [15] aimed to achieve km-anonymity by using generalization and suppression through a clustering-based anonymizer. Yao et al. [16] proposed bucketization, which separated the relationship between attributes without modifying the published data by dividing the dataset into non-overlapping subsets. These techniques are commonly referred to as anatomy [17] and slicing [18], and they are often used to anonymize a fixed number of attributes in relational databases. Recently, these disassociation-based techniques [19][20][21][22][23][24][25][26][27] have been proposed, some of which are applied to electronic health data anonymization [20][21], some of which are improved horizontal partition algorithms [19][25], and some are being considered for improving the km-anonymity-based vertical segmentation algorithm [27]. In addition, Refs. [22][23][24] are being proposed to prepare for the risk of property disclosure that can be experienced with disconnected data. J. Andrew et al. [28] proposed a fixed-spacing approach to protect sensitive medical numeric attributes and an l-diversity slicing approach to protect categories and sensitive attributes. In some studies, it is possible to carry out an analysis using a reconstructed dataset by disconnecting all cells with set values, but this is very time consuming [19].
The proposed algorithm optimizes security and CPU performance time by adopting a top-down segmentation algorithm such as the existing k-anonymity, rather than the anatomy and slicing-based previously discussed. In addition, the disadvantages of the existing k-anonymity are improved by reallocating transactions in the additional bottom-up tree search process after top-down partitioning. Compared to the existing k-anonymity, bottom-up tree search takes additional time, but the added time is a type of correction work to optimize the information loss of the remaining transactions after the anonymization of the final transaction. This algorithm takes very little time compared with the old k-anonymity algorithm for the entire process and cuts down processing time considerably compared with the HgHs technique. In terms of information loss, the proposed technique shows superior performance to other techniques developed so far, including the old k-anonymity algorithm and the HgHs technique. Figure 1 and Table 1 shows the outcomes of the proposed algorithm based on the work of Junqiang Liu and Ke Wang [14].
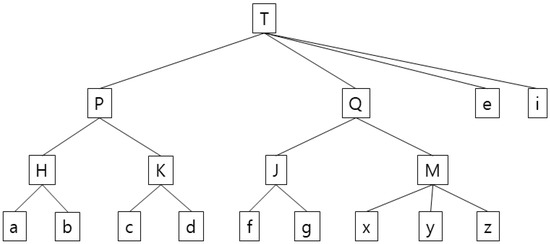
Figure 1. Example of a generalization tree for the anonymization of each item in the transactional Database D. (The values marked on each node mean a kind of item purchased by the customer (for example, when ‘a’ is peanuts and ‘b’ is walnuts, ‘H’ can be seen as nuts.)).
Table 1. Comparison with existing anonymization processing technology in the transactional Database D, composed of each item in Figure 1 (* is for suppression).
| TID | Transaction Database D | 2∞-Anonymity (Global Generalization) [1][29] | 2∞-Anonymity (Suppression) [3][4] | 2-Anonymity (Local Generalization) [5] |
HgHs [7] | Proposed Algorithm |
|---|---|---|---|---|---|---|
| 1 | b, c, d | T | *, *, d | T | P | P |
| 2 | a, f, g | T | a, f, g | P, f, g | P, f, g | P, f, g |
| 3 | d, f, y, z | T | d, f, *, * | K, f, M | P, f, M | K, f, M |
| 4 | c, d, f, x | T | *, d, f, * | K, f, M | P, f, M | K, f, M |
| 5 | a, b, c, f, g | T | a, *, *, f, g | P, f, g | P, f, g | P, f, g |
| 6 | e, i | T | e, * | T | e, * | T, i |
| 7 | e | T | e | T | e | T |
| 8 | i | T | * | T | * | i |
In Table 1, 2∞-anonymity (global generalization) [1][3] is vulnerable to excessive distortions in the presence of outliers. In k∞-anonymity, m represents km-anonymity, which is the longest transaction length. In the third column in Table 1, for example, all the items are generalized to the top level due to outliers e and I to achieve 2∞-anonymity. Since 2∞-anonymity (suppression) [7][8] or (h, k, p)-consistency uses a technique to suppress all the items, all the occurrences of b, c, i, x, y, and z in the fourth row in Table 1 are suppressed as * indicates. In 2-anonymity (local generalization) [12], which uses a top-down partitioning generalization technique—the same safety indicator as 2∞-anonymity—there is an information loss with b, c, and d generalized into T and with e, i, and e generalized into T in the fifth column in Table 1. HgHs [14] finds optimum heuristic cutting (tree separation) points and applies generalization and suppression techniques to them, having more information loss and a longer performance time than the proposed algorithm. In the sixth column in Table 1, K was generalized to a higher level of P, unlike the proposed algorithm whose T and i generalized into e and * with i suppressed, which suggests that generalizing a value is more useful than suppressing one in terms of information loss. The seventh column in Table 1 shows the performance results of the proposed algorithm. Satisfying the 2-anonymity requirement, it generalized b, c, and d into P rather than T and e and I into T, instead of treating them with T and i rather than e and * and suppressing i compared with local generalization to minimize information loss. These outcomes indicate that the proposed algorithm not only satisfies the 2-anonymity requirement, but it also causes the least information loss compared with older techniques.
2. k-Anonymity (Local Generalization) [12]
The k-anonymity algorithm is used to determine transactions that should be grouped in a generalization hierarchical tree with a top-down greedy partitioning algorithm. Figure 2 and Table 2 generalize all transactions to the root level of the hierarchy. Since all transactions share the same expression (“ALL”) after being generalized into a root, a single partition always leads to anonymization provided there are at least k number of transactions in the database. The initial partition is conveyed from this starting point to the next Anonymize routine, in which the current partition is made into a sub-partition, with Anonymize called recursively in all the outcome sub-partitions. The dividing process will end when dividing is no longer possible. Figure 2 and Table 2 is an example of the algorithm proposed in paper [12] and Figure 3 shows the pseudo-codes of the algorithm.
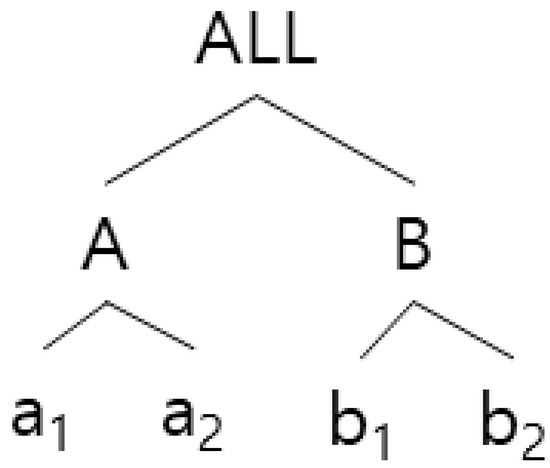
Figure 2. Example of generalization tree in transactional Database D.

Figure 3. Pseudo-codes of the k-anonymity (Local Generalization Algorithm) [12].
Table 2. Example of 2-anonymity (local generalization) according to the generalization tree in Figure 2.
| TID | Original Database D | 2-Anonymity (Local Generalization) |
|---|---|---|
| T1 | a1 | A |
| T2 | a1, a2 | A |
| T3 | b1, b2 | b1, b2 |
| T4 | b1, b2 | b1, b2 |
| T5 | a1, a2, b2 | a1, a2, B |
| T6 | a1, a2, b2 | a1, a2, B |
| T7 | a1, a2, b1, b2 | a1, a2, B |
This algorithm, however, adopts a top-down partition approach, as mentioned in the introduction. It applies the same generalization to the domains partitioned once under the generalization tree structure of each transaction item and items with a unique value, thus causing huge information loss.
3. HgHs (Heuristic Generalization Heuristic Suppression) [5]
The basic idea of the proposed technique is to integrate the global generalization technique [1][3] with the technique to suppress all items [7][8] to reinforce km-anonymity. Its detailed algorithm has two stages: generalization cuts and suppression scenarios (SSs). [Stage 1] searches for the cut of the smallest information loss in the generalization hierarchy tree with an external loop called full subtree generalization. [Stage 2] assesses if items satisfy km-anonymity in a subtree within the cut through an internal loop called total item suppression and deletes the items that do not satisfy it. As described in the [14], this algorithm is not efficient for processing large volumes of personal information threats due to its breadth-first search approach. Its CPU performance time is comparatively long, despite smaller information loss than the k-anonymity technique.
References
- Terrovitis, M.; Mamoulis, N.; Kalnis, P. Privacy preserving anonymization of set-valued data. In Proceedings of the VLDB Endowment, Auckland, New Zealand, 24–30 August 2008; pp. 115–125.
- Terrovitis, M.; Liagouris, J.; Mamoulis, N.; Skiadopoulos, S. Privacy preservation by disassociation. In Proceedings of the VLDB Endowment, Istanbul, Turkey, 27–31 August 2012; pp. 944–955.
- Terrovitis, M.; Tsitsigkos, D. Amnesia, Institute for the Management of Information Systems. Available online: https://amnesia.openaire.eu/ (accessed on 27 May 2023).
- Puri, V.; Sachdeva, S.; Kaur, P. Privacy preserving publication of relational and transaction data: Survey on the anonymization of patient data. Comput. Sci. Rev. 2019, 32, 45–61.
- Puri, V.; Kaur, P.; Sachdeva, S. (k, m, t)-anonymity: Enhanced privacy for transactional data. Concurr. Comput. Pract. Exp. 2022, 34, e7020.
- Andrew, J.; Jennifer, E.R.; Karthikeyan, J. An anonymization-based privacy-preserving data collection protocol for digital health data. Front. Public Health 2023, 11, 1125011.
- Xu, Y.; Fung, B.C.M.; Wang, K.; Fu, A.W.C.; Pei, J. Publishing sensitive transactions for itemset utility. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008.
- Xu, Y.; Wang, K.; Fu, A.W.; Yu, P.S. Anonymizing transaction databases for publication. In Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD’08), Las Vegas, NV, USA, 24–27 August 2008; pp. 767–775.
- Cao, J.; Karras, P.; Raïssi, C.; Tan, K.-L. ρ-uncertainty: Inference-proof transaction anonymization. In Proceedings of the VLDB Endowment, Singapore, 13–17 September 2010; pp. 1033–1044.
- Jia, X.; Pan, C.; Xu, X.; Zhu, K.Q.; Lo, E. ρ-uncertainty anonymization by partial suppression. In Proceedings of the International Conference on Database Systems for Advanced Applications, Bali, Indonesia, 21–24 April 2014; pp. 188–202.
- Nakagawa, T.; Arai, H.; Nakagawa, H. Personalized anonymization for set-valued data by partial suppression. Trans. Data Priv. 2018, 11, 219–237.
- He, Y.; Naughton, J. Anonymization of set-valued data via top-down, local generalization. In Proceedings of the VLDB Endowment, Lyon, France, 24–28 August 2009; pp. 934–945.
- Agrawal, R.; Srikant, R. Privacy-preserving data mining. ACM SIGMOD Rec. 2000, 29, 439–450.
- Liu, J.; Wang, K. Anonymizing transaction data by integrating suppression and generalization. In Proceedings of the 14th Pacific-Asia Conference on Knowledge Discovery and Data Mining 2010, Advances in Knowledge Discovery and Data Mining, Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6118.
- Loukides, G.; Gkoulalas-Divanis, A. Utility-aware anonymization of diagnosis codes. IEEE J. Biomed. Health Inform. 2013, 17, 60–70.
- Yao, L.; Chen, Z.; Wang, X.; Liu, D.; Wu, G. Sensitive label privacy preservation with anatomization for data publishing. IEEE Trans. Dependable Secur. Comput. 2021, 18, 904–917.
- Xiao, X.; Tao, Y. Anatomy: Simple and effective privacy preservation. In Proceedings of the VLDB Endowment, Seoul, Republic of Korea, 12–15 September 2006; pp. 139–150.
- Li, T.; Li, N.; Zhang, J.; Molloy, I. Slicing: A new approach to privacy preserving data publishing. IEEE Trans. Knowl. Data Eng. 2012, 24, 561–574.
- Awad, N.; Couchot, J.-F.; Bouna, B.A.; Philippe, L. Publishing anonymized set-valued data via disassociation towards analysis. Future Internet 2020, 12, 71.
- Loukides, G.; Liagouris, J.; Gkoulalas-Divanis, A.; Terrovitis, M. Disassociation for electronic health record privacy. J. Biomed. Inform. 2014, 50, 46–61.
- Loukides, G.; Liagouris, J.; Gkoulalas-Divanis, A.; Terrovitis, M. Utility-constrained electronic health record data publishing through generalization and disassociation. In Medical Data Privacy Handbook; Gkoulalas-Divanis, A., Loukides, G., Eds.; Springer: Cham, Switzerland, 2015; pp. 149–177.
- Sara, B.; Al Bouna, B.; Mohamed, N.; Christophe, G. On the evaluation of the privacy breach in disassociated set-valued datasets. In Proceedings of the 13th International Joint Conference on e-Business and Telecommunications, Lisbon, Portugal, 26–28 July 2016; pp. 318–326.
- Awad, N.; Al Bouna, B.; Couchot, J.F.; Philippe, L. Safe disassociation of set-valued datasets. J. Intell. Inf. Syst. 2019, 53, 547–562.
- Puri, V.; Kaur, P.; Sachdeva, S. Effective removal of privacy breaches in disassociated transactional datasets. Arab. J. Sci. Eng. 2020, 45, 3257–3272.
- Awad, N.; Couchot, J.F.; Al Bouna, B.; Philippe, L. Ant-driven clustering for utility-aware disassociation of set-valued datasets. In Proceedings of the 23rd International Database Applications and Engineering Symposium, Athens, Greece, 10–12 June 2019; pp. 1–9.
- Bewong, M.; Liu, J.; Liu, L.; Li, J.; Choo1, K.-K.R. A relative privacy model for effective privacy preservation in transactional data. Concurr. Comput. Pract. Exp. 2019, 31, e4923.
- Liu, X.; Feng, X.; Zhu, Y. Transactional data anonymization for privacy and information preservation via disassociation and local suppression. Symmetry 2022, 14, 472.
- Andrew Onesimu, J.; Karthikeyan, J.; Jennifer, E.; Marc, P.; Hien, D. Privacy preserving attribute-focused anonymization scheme for healthcare data publishing. IEEE Access 2022, 10, 86979–86997.
- Cunha, M.; Mendes, R.; Vilela, J.P. A survey of privacy-preserving mechanisms for heterogeneous data types. Comput. Sci. Rev. 2021, 41, 100403.
More
Information
Subjects:
Computer Science, Information Systems
Contributor
MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register
:
View Times:
677
Revisions:
2 times
(View History)
Update Date:
26 Jul 2023
Notice
You are not a member of the advisory board for this topic. If you want to update advisory board member profile, please contact office@encyclopedia.pub.
OK
Confirm
Only members of the Encyclopedia advisory board for this topic are allowed to note entries. Would you like to become an advisory board member of the Encyclopedia?
Yes
No
${ textCharacter }/${ maxCharacter }
Submit
Cancel
Back
Comments
${ item }
|
More
No more~
There is no comment~
${ textCharacter }/${ maxCharacter }
Submit
Cancel
${ selectedItem.replyTextCharacter }/${ selectedItem.replyMaxCharacter }
Submit
Cancel
Confirm
Are you sure to Delete?
Yes
No




