You're using an outdated browser. Please upgrade to a modern browser for the best experience.

Submitted Successfully!
Thank you for your contribution! You can also upload a video entry or images related to this topic.
For video creation, please contact our Academic Video Service.
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Quanyong Lu | -- | 3371 | 2023-06-19 11:15:59 | | | |
| 2 | Sirius Huang | Meta information modification | 3371 | 2023-06-20 03:17:39 | | |
Video Upload Options
We provide professional Academic Video Service to translate complex research into visually appealing presentations. Would you like to try it?
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Li, R.; Liu, F.; Lu, Q. Quantum Light Source Based on Semiconductor Quantum Dots. Encyclopedia. Available online: https://encyclopedia.pub/entry/45779 (accessed on 23 December 2025).
Li R, Liu F, Lu Q. Quantum Light Source Based on Semiconductor Quantum Dots. Encyclopedia. Available at: https://encyclopedia.pub/entry/45779. Accessed December 23, 2025.
Li, Rusong, Fengqi Liu, Quanyong Lu. "Quantum Light Source Based on Semiconductor Quantum Dots" Encyclopedia, https://encyclopedia.pub/entry/45779 (accessed December 23, 2025).
Li, R., Liu, F., & Lu, Q. (2023, June 19). Quantum Light Source Based on Semiconductor Quantum Dots. In Encyclopedia. https://encyclopedia.pub/entry/45779
Li, Rusong, et al. "Quantum Light Source Based on Semiconductor Quantum Dots." Encyclopedia. Web. 19 June, 2023.
Copy Citation
Quantum light sources that generate single photons and entangled photons have important applications in the fields of secure quantum communication and linear optical quantum computing. Self-assembled semiconductor quantum dots, also known as “artificial atoms”, have discrete energy-level structures due to electronic confinement in all three spatial dimensions. It has the advantages of high stability, high brightness, deterministic, and tunable emission wavelength, and is easy to integrate into an optical microcavity with a high-quality factor, which can realize a high-performance quantum light source.
quantum information
single-photon source
entangled photon source
semiconductor quantum dots
1. Introduction
With the rapid development of an information-based society, the demand for high-speed information processing and secure information communication is undergoing a tremendous increase. At present, integrated circuit technology is approaching the physical limits in terms of material and process technologies. Moore’s law [1] is slowing down gradually, and the development of traditional computing technology is facing a systemic dilemma. Quantum information technology, based on the principles of quantum mechanics, provides a solution to future needs to a certain extent. Since quantum information was proposed in 1982 [2], with the establishment of quantum key distribution [3], Deutsch–Jozsa equilibrium function algorithm [4], invisible quantum transfer [5], Shor large number prime factorization algorithm [6], Grover’s search algorithm [7], etc., quantum communication [8], quantum computing [9], quantum storage [10], and quantum radar [11], has gained an exceptionally rapid development. In particular, the three quantum technologies with quantum light sources, quantum coding, regulation and transmission, and single-photon emission and detection as the core are the key parts of developing quantum communication. Studies have shown that quantum communication based on single-photon sources has an absolute security and high efficiency, whereas the acquisition of reliable and easily available single-photon sources is a bottleneck to promoting the development of related technologies. Therefore, an in-depth study of high-quality single-photon sources becomes of great value. Quantum bits, as the most fundamental unit of quantum information, can be physically realized in a variety of systems, including photons, cold atoms, ion traps, superconducting loops, nuclear spins, etc. [12][13][14][15][16]. Among them, optical quantum bits as flying quantum bits are an excellent choice for quantum communication and quantum computing. Currently, the main methods for preparing single-photon states are attenuating laser sources [17], i.e., using spontaneous nonlinear optical processes in nonlinear materials [18] and spontaneous radiation generation of single photons from two-energy systems based on different atoms or atom-like levels, such as single atoms [19], single molecules [20], diamond color centers [21], defect states in two-dimensional materials [22][23], and semiconductor quantum dots (QDs) [24]. Among them, the semiconductor QDs are a kind of quasi-zero-dimensional nanometer material and have excellent photonic properties, which can be used to generate single photons and entangled photon pairs. Furthermore, the linewidth of their emitted photons is the ability to be radiative lifetime limited, and it is highly compatible with modern semiconductor manufacturing processes, enabling large-scale integration and scaling of quantum emitters on semiconductor chips. Therefore, semiconductor QD technology is one of the best solutions for single-photon sources to move further toward practicality.
2. Ideal Single Photon Source
From the statistical point of view of light emission, light has been divided into two main categories: classical light sources containing thermally radiated light with coherent light and non-classical light sources containing fluorescently radiated light [25]. The photons emitted from a typical ordinary thermal radiation light source represented by incandescent lamps exhibit Bunching, which satisfies the Super Poissonian in terms of photon number distribution and is characterized by a very high probability of simultaneous reception of multiple photons within a short delay time interval. The coherent light source represented by the laser, which emits photons with randomization, satisfies the Poissonian distribution, which shows that the probability of detecting two photons at the same time is the same. There is neither a fixed time interval nor any correlation between the two photons. In contrast, the quantum light source is represented by the single-photon source, which emits photons showing antibunching, which satisfies the Sub Poissonian distribution and exhibits no simultaneous detection of two photons at the zero moment (t = 0) and a fixed time interval between the successive emitted photons.
The ideal single-photon source has and produces only one photon at a time. The main criteria for judging the quality of a single-photon source are two-photon suppression, indistinguishability, and efficiency.
2.1. Single-Photon Purity
It is essential to develop precise experimental methods to assess the quality of a single-photon source. Is a very important index for judging a single-photon source is the second-order correlation function g(2)(τ); the photon statistics of a quantum state of light are determined by recording g(2)(τ) defined as [26]:
where 𝑎̂ and 𝑎̂ † are annihilation and creation operators for the optical mode probed in the experiment. g(2)(τ) indicates the probability of detecting a photon at each moment t and t + τ. The g(2)(0) = 1 − 1/N for the Fock state with photon number N. Only the superposition of the single-photon state and the vacuum state can get g(2)(0) = 0. All other states obtain this value as positive, so the closer this value is to 0, the better the single-photon nature is. At that time, g(2)(0) = 0, the probability of multiphoton is 0, and the anti-collective beam effect is presented. In addition, g(2)(0) = 1 for ordinary coherent light (laser) and g(2)(0) = 2 for thermal sources, g(2)(0) can be employed as a measure of the single-photon purity of a light source. Experimentally, the second-order correlation function of photons is generally measured by the Hanbury Brown and Twiss (HBT) interferometer [27] shown in Figure 1.

Figure 1. HBT interferometer to detect the second-order correlation coefficient g(2)(0).
2.2. Photon Indistinguishability
The single-photon source with only two-photon suppression cannot fully meet the application requirements of linear optical quantum computing and quantum networks. Since photon identity plays an important role in the realization of double-bit or multi-bit quantum logic gates, single-photon sources are also required. The photons emitted by the source are identical. When a photon is incident on a 50:50 beam splitter, it will be transmitted or reflected with half the probability. When two identical photons are incident from both ends of the beam splitter, the following four possible results will appear. Since the photon will introduce a phase jump of π/2 when reflected on the beam splitter, the corresponding probability amplitude distributions of the four situations are shown in Figure 2. The two cases in the middle of Figure 2 cancel out because the probability amplitudes are opposite, and the two photons are emitted in the same direction. This phenomenon is Hong–Ou–Mandel (HOM) interference [28]. In experiments, the photon indistinguishability is judged by measuring the HOM interference contrast of two photons emitted by a single quantum dot. The luminescent dipoles in the atomic-like structure are often in a complex lattice environment, affected by lattice vibrations (phonons), resulting in decoherence and broadening of the energy spectrum of the fluorescent photons, thereby reducing photon indistinguishability.
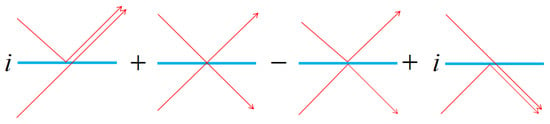
Figure 2. The possible output results and probability amplitudes of two photons incident through a 50:50 beam splitter.
2.3. Single-Photon Efficiency
The efficiency includes the single-photon generation efficiency and the collection efficiency. The single-photon generation efficiency is the probability that a single photon is produced by a single-photon source under a single pulse excitation. For an ideal deterministic single-photon source, one and only one photon is produced for each pulse excitation. Since the QD is inside a high refractive index group III-V semiconductor material, when photons exit the sample, most of the photons cannot be collected effectively by the optical system due to total reflection. As shown in Figure 3a, for example, for the interface between GaAs (n1 = 3.59) and air (n2 = 1), the angle of total reflection inward is small:
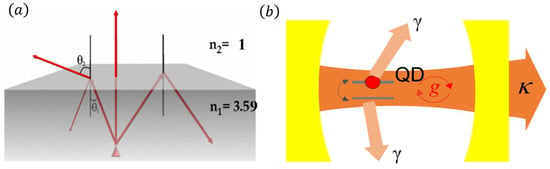
Figure 3. (a) Schematic diagram of the inward total reflection angle of GaAs material; (b) Interaction of the two-energy system with the cavity.
When the angle of incidence of photons arriving at the GaAs surface is greater than 𝜃c, the photons will be completely reflected inward and cannot be detected by the detector. Where the outgoing stereo angle of photons leaving the GaAs surface is:
Since photons generated by a single-photon source tend to exit along a 4π space angle, the collection efficiency is:
Clearly, the low collection efficiency is due to the lack of a proper cavity for strong coupling and efficient outcoupling.
The generation of single photon or photon pairs in QD is deterministic in its nature. However, efficient extraction of single photon or photon pairs from the high index semiconductor material requires the engineering of the photonic environment. In fact, the extraction efficiency can be even lower, considering the factors such as sample surface roughness and material absorption. Therefore, there is a great need to enhance the photon collection efficiency. Experimentally, researchers usually use the method of optical microcavities or waveguide structures (such as nanowires, microlenses, metasurfaces, etc.) to enhance the efficiency of photon extraction. Figure 3b shows the typical single-photon source consisting of a single QD coupled coherently, with coupling constant g, to one mode of a Fabry–Pérot cavity. Incoherent processes are spontaneous emission from the nonclassical light emitter to the continuum at rate γ and photon loss through the cavity mirrors at rate κ. Integrating quantum dots into optical microcavities can channel the spontaneously emitted photons into a well-defined spatial mode and in a desired direction to improve the overall efficiency. It can alter the spectral width of the emission. It can also provide an environment where dissipative mechanisms are overcome so that a pure quantum-state emission takes place. By coupling with an optical microcavity, the interaction between the cavity mode and quantum energy levels can be greatly enhanced. Depending on the relationship between the strength of the coupling and the decay rate, the coupling system can be divided into weakly coupled and strongly coupled systems [29][30]. In the strong coupling region [31], the intrinsic energy of semiconductor quantum dot energy level and microcavity optical field mode coupling is split, and the split energy is [32]:
where 𝐸𝑥 and 𝐸𝑐 are the energies of the QD exciton and cavity modes, 𝛾𝑥 and 𝛾c are their full-width half-maximum (FWHM), Δ=𝐸𝑥−𝐸𝑐 is the detuning, and g is the exciton-cavity coupling strength. Strong coupling requires 𝑔2>(𝛾𝑐−𝛾𝑥)2/16, which leads to a splitting of the two eigenenergies at resonance (Δ=0) by an amount called the vacuum Rabi splitting. For typical QD and microcavities, 𝛾𝑥 (a few μeV) is much smaller than 𝛾c (~100 μeV), and the strong coupling condition reduces to 𝑔>𝛾𝑐/4. In order to reach strong coupling with a given oscillator strength, one must maximize the ratio of cavity quality factor to mode volume [33]. In addition, in the strong-coupling regime, due to the coupling of the QD to a privileged cavity mode is far stronger than its coupling to all other modes, so the ensuing process of spontaneous emission becomes deterministic.
When the coupling strength is less than the decay rate, the coupling system is weakly coupled. In this case, the spontaneous radiation rate of the QD is enhanced due to the increase of the local field density of states, and the enhancement is a multiple of the Purcell factor, which is the Purcell effect. It, therefore, can be used to optimize the performance of optical devices such as lasers and quantum light sources. The maximum Purcell factor is obtained when the QD is located at the position with the maximum field strength [34][35]:
where 𝜆 is the resonant wavelength, n is the refractive index of the dielectric material in the microcavity, Q is the quality factor of the cavity, and V is the mode volume in the cavity. In fact, Fp will be far from the optimal value because of the existence of detuning between quantum dots and microcavities and other problems. When Fp < 1, the spontaneous radiation rate of quantum dots will be suppressed; when Fp > 1, the spontaneous radiation rate of quantum dots will be enhanced, which means more single photons will be radiated by quantum dots per unit time. From the definition, it can be seen that a small mode volume and a large quality factor can lead to an increase in the spontaneous radiation rate. The microcavity structure that can be coupled with the QD can effectively modulate the quantum dot luminescence performance by a proper design of microcavity parameters and the combination of semiconductor growth process conditions of the microcavity structure. When the QDs are located in the center of the cavity mode, the QD and the cavity can achieve good coupling efficiency (𝛽=𝐹𝑝1+𝐹𝑝), and it will play a great role in enhancing the emission rate of QD.
3. Self-Assembled Semiconductor Quantum Dots
3.1. Growth of Self-Assembled Semiconductor Quantum Dots
Currently, single-photon emission has been experimentally observed in different atomic and atom-like systems such as atoms, ions, molecules, NV color centers, and QD. Among them, the growth of self-assembled semiconductor QD mainly by molecular beam epitaxy (MBE) or metal-organic compound chemical vapor deposition (MOCVD) is of great interest because of its solid-structure stability and discrete atom-like energy level structure recognized as a strong contender for achieving high-quality single-photon sources in solid-state systems. In addition, QDs can be excited with double excitons or even multiple excitons, generating frequency-distinguishable photon pairs or a sequence of photons of different frequencies through a cascade of fouling processes, each of which is a single photon at each frequency.
InAs/GaAs QDs are a kind of self-assembled semiconductor nanostructures that are widely studied in experiments nowadays. It is generally formed by growing InAs QD on GaAs material in Stranski–Krastanow (S–K) growth mode [36]. Since there is a constant lattice mismatch of about 7% on GaAs, InAs adapt to the lattice mismatch by elastic strain. The GaAs buffer layer is grown first, and then the precipitation of InAs continues on the GaAs buffer layer. Initially, InAs is grown in two dimensions to form the infiltrated layer. Since the InAs lattice structure is larger than that of the GaAs substrate, the epitaxial layer is compressed laterally, and stress is generated, which increases with the thickness of InAs. When the deposited amount exceeds the critical value, the accumulated elastic energy is released, and the three-dimensional growth begins, forming InAs QDs. The QDs are formed randomly on the surface of GaAs material, and the height of these QDs is around 1~10 nm, and the diameter is around 10~70 nm [37]. The size of the dots has a great influence on the spectral lines of QD fluorescence, and the larger the difference in the size of QDs, the larger the difference in the fluorescence emission wavelength of QDs. In addition, due to the random distribution of self-assembled semiconductor QD leading to a very low yield of single-photon sources, in order to make the QD coupled to microcavities controllable, the determination of the position of the self-organized grown QD using different optical positioning methods (without damage) has been proposed [38][39]. It should be noted that the semiconductor QD growth method given here is not limited to InAs/GaAs QDs, but is also applicable to QDs of other semiconductor materials.
3.2. Band Structure of Self-Assembled Semiconductor Quantum Dots
Since the size of the MBE-grown self-assembled semiconductor QD in the growth direction is smaller than that in the lateral direction, the energy level splitting in the growth direction (z-direction) of the self-assembled semiconductor QD is much larger than the energy splitting in the lateral direction. For the InAs/GaAs QD shown in Figure 4a, the InAs QD material is grown in the GaAs material. The energy band of InAs/GaAs QD is divided into conduction bands and valence bands, in which the fluctuation equation of the ground state electron in the conduction band shows s-wave symmetry, the spin angular momentum of the electron is 1/2, and the spin Sz = ±1/2 in the z-axis direction. In contrast, the ground state hole in the valence band shows p-wave symmetry. The angular momentum of the holes is 3/2. The holes in the z-axis direction are divided into heavy holes and light holes, with the spin component Jz = ±3/2 in the z-axis direction for heavy holes and Jz = ±1/2 in the z-axis direction for light holes; there is also a spin-orbit splitting energy band in the valence band, which has a spin of Sz = 1/2 and a spin of Jz = ±1/2 in the z-axis direction. Since the heavy hole levels are far apart, we consider only the effect of heavy holes when discussing the structure of the excitonic state of InAs/GaAs quantum dots. Optical excitation of semiconductor QD allows studying the energy level structure of QD, which also is the most common method to obtain single photons. Optically excited semiconductor QD can be divided into non-resonantly excited QDs (including band excitation and p-shell excitation) and resonantly excited QD (including pulsed resonant excitation-Raby oscillation and continuous resonant excitation-Mollow triplet state). Before the QD is excited, there are no additional charged particles inside the QD, and the excitation produces an electron-hole pair called neutral exciton |X〉|X〉 (Excitons are formed due to the Coulomb interaction of electrons and holes with each other), in which the electrons and holes occupy the lowest energy levels of the conduction band and valence band, respectively. Since the optical selection law dictates that only transitions with total angular momentum M = ± 1 occur in photon absorption, if the spins of electrons and heavy holes are antiparallel, excitons with the angular momentum of ±1 on the z-axis ((Sz = 1/2, Jz = −3/2) or (Sz = −1/2, Jz = 3/2)) satisfy the transitions, it is called a bright exciton. If the spins of the electron and heavy hole are parallel and the angular momentum component of the exciton in the z-axis is ±2 ((Sz = 1/2, Jz =3/2) or (Sz =−1/2, Jz = −3/2)) is forbidden transitions, it is called a dark exciton [40]. QDs with a high degree of structural symmetry emit fluorescence spectral lines without dark excitons, only bright excitons. However, when the symmetry is broken by external factors (e.g., transverse magnetic field), a mixture of bright and dark excitons is generated, and the dark exciton component also appears in the fluorescence spectral line emitted by the QD.
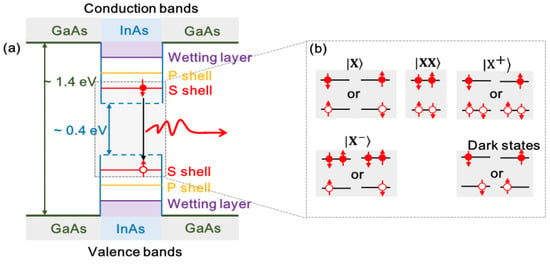
Figure 4. (a) Energy level structure of InAs/GaAs QD; (b) Schematic diagram of neutral exciton and charged exciton.
When the InAs/GaAs QD is excited through up the band, the photon energy of the excitation light is larger than the forbidden band width of GaAs around the QD. The electron-hole pair formed between the conduction band and the valence band undergoes a spontaneous relaxation process, and a part of the electrons and holes are trapped by the infiltration layer and then reach the lowest excited state of the QD after a phonon-assisted relaxation process of several tens of picoseconds to form an exciton. As shown in Figure 4b, when the QD captures an electron and a hole, a neutral exciton |X〉|X〉 is formed due to the Coulomb interaction between the electron and the hole. When the quantum dot captures two electrons and a hole, the exciton formed is the charged exciton |X−〉|X−〉. The same process can occur with two holes and one electron |X+〉|X+〉, two electrons and two holes |XX〉|XX〉 (double exciton), etc. In contrast to charged excitons, neutral excitons have exchange interactions between electrons and holes. Due to the irregularity of the QD growth process, there is fine structure cleavage of energy levels even without an external magnetic field, while in charged excitons, the total angular momentum of the two electrons in the conduction band is zero, and there are no exchange interactions. At the same time, the neutral exciton |X〉|X〉 has a Coulomb interaction of one electron and one hole, while the charged exciton |X−〉|X−〉 has a three-body Coulomb interaction of two electrons and one hole, and the energy of the charged exciton |X−〉|X−〉 is smaller than that of the neutral exciton. The Coulomb interactions of different excitons and the fluorescence photon energy emitted is also different. This Coulomb reformation process can be distinguished from the different exciton states of QD by spectral analysis, and the fluorescence generated by band excitation contains multiple exciton components. Since the excitation time from electron-hole generation to relaxation to exciton formation in QDs is less than the radiative lifetime of QD fluorescence (~1 ns), QDs have and will have only one fluorescent photon for each excitation. It should be noted that the analysis of the band structure of semiconductor QDs given here is not limited to InAs/GaAs QDs, but is also applicable to QDs of other semiconductor materials.
References
- Yablonovitch, E. Inhibited Spontaneous Emission in Solid-State Physics and Electronics. Phys. Rev. Lett. 1987, 58, 2059–2062.
- Feynman, R.P. Simulating physics with computers. In Feynman and Computation; CRC Press: Boca Raton, FL, USA, 2018; pp. 133–153.
- Xu, F.; Ma, X.; Zhang, Q.; Lo, H.-K.; Pan, J.-W. Secure quantum key distribution with realistic devices. Rev. Mod. Phys. 2020, 92, 025002.
- Deutsch, D.; Jozsa, R. Rapid solution of problems by quantum computation. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1992, 439, 553–558.
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895.
- Shor, P.W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 1999, 41, 303–332.
- Grover, L.K. Quantum computers can search arbitrarily large databases by a single query. Phys. Rev. Lett. 1997, 79, 4709.
- Duan, L.M.; Lukin, M.D.; Cirac, J.I.; Zoller, P. Long-distance quantum communication with atomic ensembles and linear optics. Nature 2001, 414, 413–418.
- DiVincenzo, D.P. Quantum computation. Science 1995, 270, 255–261.
- Bao, X.-H.; Reingruber, A.; Dietrich, P.; Rui, J.; Dück, A.; Strassel, T.; Li, L.; Liu, N.-L.; Zhao, B.; Pan, J.-W. Efficient and long-lived quantum memory with cold atoms inside a ring cavity. Nat. Phys. 2012, 8, 517–521.
- Maccone, L.; Ren, C. Quantum radar. Phys. Rev. Lett. 2020, 124, 200503.
- O’brien, J.L.; Furusawa, A.; Vučković, J. Photonic quantum technologies. Nat. Photonics 2009, 3, 687–695.
- Bloch, I. Quantum coherence and entanglement with ultracold atoms in optical lattices. Nature 2008, 453, 1016–1022.
- Häffner, H.; Roos, C.F.; Blatt, R. Quantum computing with trapped ions. Phys. Rep. 2008, 469, 155–203.
- Clarke, J.; Wilhelm, F.K. Superconducting quantum bits. Nature 2008, 453, 1031–1042.
- Scappucci, G.; Kloeffel, C.; Zwanenburg, F.A.; Loss, D.; Myronov, M.; Zhang, J.-J.; De Franceschi, S.; Katsaros, G.; Veldhorst, M. The germanium quantum information route. Nat. Rev. Mater. 2021, 6, 926–943.
- Zhou, L.; Lin, J.; Jing, Y.; Yuan, Z. Twin-field quantum key distribution without optical frequency dissemination. Nat. Commun. 2023, 14, 928.
- Politi, A.; Cryan, M.J.; Rarity, J.G.; Yu, S.; O’Brien, J.L. Silica-on-silicon waveguide quantum circuits. Science 2008, 320, 646–649.
- Darquié, B.; Jones, M.P.A.; Dingjan, J.; Beugnon, J.; Bergamini, S.; Sortais, Y.; Messin, G.; Browaeys, A.; Grangier, P. Controlled single-photon emission from a single trapped two-level atom. Science 2005, 309, 454–456.
- Lounis, B.; Moerner, W.E. Single photons on demand from a single molecule at room temperature. Nature 2000, 407, 491–493.
- Sipahigil, A.; Jahnke, K.D.; Rogers, L.J.; Teraji, T.; Isoya, J.; Zibrov, A.S.; Jelezko, F.; Lukin, M.D. Indistinguishable photons from separated silicon-vacancy centers in diamond. Phys. Rev. Lett. 2014, 113, 113602.
- He, Y.M.; Clark, G.; Schaibley, J.R.; Chen, M.-C.; Wei, Y.-J.; Ding, X.; Zhang, Q.; Yao, W.; Xu, X.; Lu, C.-Y.; et al. Single quantum emitters in monolayer semiconductors. Nat. Nanotechnol. 2015, 10, 497–502.
- Tran, T.T.; Bray, K.; Ford, M.J.; Toth, M.; Aharonovich, I. Quantum emission from hexagonal boron nitride monolayers. Nat. Nanotechnol. 2016, 11, 37–41.
- Senellart, P.; Solomon, G.; White, A. High-performance semiconductor quantum-dot single-photon sources. Nat. Nanotechnol. 2017, 12, 1026–1039.
- Michler, P. Nonclassical light from single semiconductor quantum dots. In Single Quantum Dots: Fundamentals, Applications, and New Concepts; Springer: Berlin/Heidelberg, Germany, 2003; pp. 315–347.
- Fischer, K.A.; Müller, K.; Lagoudakis, K.G.; Vučković, J. Dynamical modeling of pulsed two-photon interference. New J. Phys. 2016, 18, 113053.
- Hanbury Brown, R.; Twiss, R.Q. A test of a new type of stellar interferometer on Sirius. Nature 1956, 178, 1046–1048.
- Hong, C.K.; Ou, Z.Y.; Mandel, L. Measurement of subpicosecond time intervals between two photons by interference. Phys. Rev. Lett. 1987, 59, 2044.
- Khitrova, G.; Gibbs, H.M.; Kira, M.; Koch, S.W.; Scherer, A. Vacuum Rabi splitting in semiconductors. Nat. Phys. 2006, 2, 81–90.
- Vahala, K.J. Optical microcavities. Nature 2003, 424, 839–846.
- Hennessy, K.; Badolato, A.; Winger, M.; Gerace, D.; Atatüre, M.; Gulde, S.; Fält, S.; Hu, E.L.; Imamoğlu, A. Quantum nature of a strongly coupled single quantum dot–cavity system. Nature 2007, 445, 896–899.
- Reithmaier, J.P.; Sęk, G.; Löffler, A.; Hofmann, C.; Kuhn, S.; Reitzenstein, S.; Keldysh, L.V.; Kulakovskii, V.D.; Reinecke, T.L.; Forchel, A. Strong coupling in a single quantum dot–semiconductor microcavity system. Nature 2004, 432, 197–200.
- Yoshie, T.; Scherer, A.; Hendrickson, J.; Khitrova, G.; Gibbs, H.M.; Rupper, G.; Ell, C.; Shchekin, O.B.; Deppe, D.G. Vacuum Rabi splitting with a single quantum dot in a photonic crystal nanocavity. Nature 2004, 432, 200–203.
- Benson, O. Assembly of hybrid photonic architectures from nanophotonic constituents. Nature 2011, 480, 193–199.
- Kimble, H.J. The quantum internet. Nature 2008, 453, 1023–1030.
- Stranski, I.N.; Krastanow, L. Zur Theorie der orientierten Ausscheidung von Ionenkristallen aufeinander. Mon. Chem. Verwandte Teile And. Wiss. 1937, 71, 351–364.
- Marquez, J.; Geelhaar, L.; Jacobi, K. Atomically resolved structure of InAs quantum dots. Appl. Phys. Lett. 2001, 78, 2309–2311.
- Gschrey, M.; Gericke, F.; Schüßler, A.; Schmidt, R.; Schulze, J.-H.; Heindel, T.; Rodt, S.; Strittmatter, A.; Reitzenstein, S. In situ electron-beam lithography of deterministic single-quantum-dot mesa-structures using low-temperature cathodoluminescence spectroscopy. Appl. Phys. Lett. 2013, 102, 251113.
- Nowak, A.K.; Portalupi, S.L.; Giesz, V.; Gazzano, O.; Savio, C.D.; Braun, P.-F.; Karrai, K.; Arnold, C.; Lanco, L.; Sagnes, I.; et al. Deterministic and electrically tunable bright single-photon source. Nat. Commun. 2014, 5, 3240.
- Lodahl, P.; Mahmoodian, S.; Stobbe, S. Interfacing single photons and single quantum dots with photonic nanostructures. Rev. Mod. Phys. 2015, 87, 347–400.
More
Information
Subjects:
Physics, Applied
Contributors
MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register
:
View Times:
855
Revisions:
2 times
(View History)
Update Date:
20 Jun 2023
Notice
You are not a member of the advisory board for this topic. If you want to update advisory board member profile, please contact office@encyclopedia.pub.
OK
Confirm
Only members of the Encyclopedia advisory board for this topic are allowed to note entries. Would you like to become an advisory board member of the Encyclopedia?
Yes
No
${ textCharacter }/${ maxCharacter }
Submit
Cancel
Back
Comments
${ item }
|
More
No more~
There is no comment~
${ textCharacter }/${ maxCharacter }
Submit
Cancel
${ selectedItem.replyTextCharacter }/${ selectedItem.replyMaxCharacter }
Submit
Cancel
Confirm
Are you sure to Delete?
Yes
No




