You're using an outdated browser. Please upgrade to a modern browser for the best experience.

Submitted Successfully!
Thank you for your contribution! You can also upload a video entry or images related to this topic.
For video creation, please contact our Academic Video Service.
Video Upload Options
We provide professional Academic Video Service to translate complex research into visually appealing presentations. Would you like to try it?
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Li, D.; He, W.; Shi, S.; Wu, B.; Xiao, Y.; Lin, Q.; Li, L. Atom Chips for Absolute Gravity Sensors. Encyclopedia. Available online: https://encyclopedia.pub/entry/45270 (accessed on 01 January 2026).
Li D, He W, Shi S, Wu B, Xiao Y, Lin Q, et al. Atom Chips for Absolute Gravity Sensors. Encyclopedia. Available at: https://encyclopedia.pub/entry/45270. Accessed January 01, 2026.
Li, Dezhao, Wenfeng He, Shengnan Shi, Bin Wu, Yuhua Xiao, Qiang Lin, Long Li. "Atom Chips for Absolute Gravity Sensors" Encyclopedia, https://encyclopedia.pub/entry/45270 (accessed January 01, 2026).
Li, D., He, W., Shi, S., Wu, B., Xiao, Y., Lin, Q., & Li, L. (2023, June 07). Atom Chips for Absolute Gravity Sensors. In Encyclopedia. https://encyclopedia.pub/entry/45270
Li, Dezhao, et al. "Atom Chips for Absolute Gravity Sensors." Encyclopedia. Web. 07 June, 2023.
Copy Citation
As a powerful tool in scientific research and industrial technologies, the cold atom absolute gravity sensor (CAGS) based on cold atom interferometry has been proven to be the most promising new generation high-precision absolute gravity sensor. However, large size, heavy weight, and high–power consumption are still the main restriction factors of CAGS being applied for practical applications on mobile platforms. Combined with cold atom chips, it is possible to drastically reduce the complexity, weight, and size of CAGS.
atom chips
absolute gravity sensor
cold atom
1. Introduction
The absolute gravity sensor has been proven to be a powerful tool in scientific research and industrial technologies. In scientific research areas, it is considered to be a powerful tool to detect weak equivalence principle (WEP) violations [1][2], which can directly imply the equivalence between inertial and gravitational mass. Moreover, as a powerful tool, the absolute gravity sensor also has been widely applied to searching for dark energy [3][4], gravitational waves [5][6], determining the Newtonian gravitational constant G [7][8], short–range forces [9][10] and so on. On the other hand, this sensor has been widely applied in industrial areas including inertial navigation [11][12], archeology [13][14], monitoring earthquakes [15][16], groundwater [17][18], resource exploration [19][20], and many other applications.
Cold atom absolute gravity sensors (CAGSs) based on cold atom interferometry have been proven to be the most promising new generation absolute gravity sensor [21][22]. The prototype of the cold atom gravimeter was demonstrated by Steven Chu’s group at Stanford University, in 1991 [23]. The research of CAGSs has made great progress over the last 30 years. Different from the classical optical absolute gravity sensor using mechanical mass as a free-falling object, CAGSs use the cold atom cluster as the free–falling object to sense the gravity with the advantages of better stability, a long service life [24][25] and a high sampling rate [25]. The sensitivity and accuracy of CAGSs have exceeded the performance of the traditional optical absolute gravimeter of FG-5 [24][25]. As reported, the uncertainty of a CAGS was demonstrated to be high, up to 1.3 μGal Gal (1 μGal = 10−8 m/s2) [26], while the sensitivity of a CAGS can also be high, up to 4.2 μGal/Hz−−−√4.2 Gal/Hz [27]. There are many research groups involved in this research area and some reported representative works of CAGSs are summarized in Table 1. The early research of CAGSs mainly focused on improving sensitivity and stability. Over the past decade, researchers gradually shifted their attention to miniaturization and applications of CAGSs. Portable CAGSs have been demonstrated to be applicable on various mobile platforms, including vehicles [28][29], shipboard [30][31], airborne [32][33], and even in aerospace [18][34][35]. However, weight, power consumption, and noise in a dynamic environment are still the main restriction factors of CAGSs being applied for practical applications, especially on mobile platforms [16][19][34][36][37]. Many different strategies have been proposed to solve these problems, and using atom chips is one of the most promising methods, since they can significantly reduce the complexity, weight, and size of CAGSs.
An atom chip was originally proposed to miniaturize setups of cold atom systems using some mature technologies in integrated circuit areas [43][44]. The first atom chip was reported in 1999 [45], and only a few years later the Bose–Einstein condensation (BEC) was realized with an atom chip [46][47]. Subsequently, the development of atom chips has brought many significant changes and surprises to cold atom sensors including CAGSs, as in Figure 1.
An atom chip was originally proposed to miniaturize setups of cold atom systems using some mature technologies in integrated circuit areas [43][44]. The first atom chip was reported in 1999 [45], and only a few years later the Bose–Einstein condensation (BEC) was realized with an atom chip [46][47]. Subsequently, the development of atom chips has brought many significant changes and surprises to cold atom sensors including CAGSs, as in Figure 1.
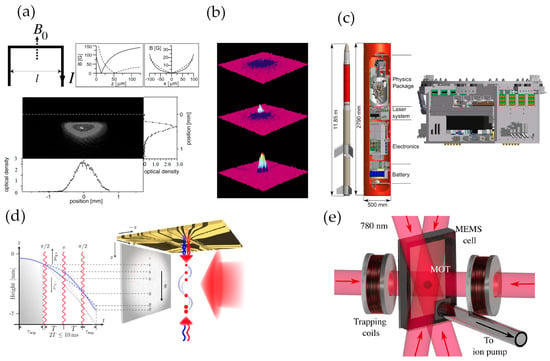
Figure 1. (a) Wire layout of an atom chip for quadrupole potential with generated magnetic potentials and an image of a cold atom cloud (photo reproduced with permission from American Physical Society) [45]; (b) Time–of–flight absorption images of BEC generated with an atom chip (photo reproduced with permission from Springer Nature) [47]; (c) the Matter–wave Interferometry in Microgravity (MAIUS) rocket (photo reproduced with permission from Springer Nature) [48]; (d) Atom–chip based gravimeter and space-time trajectories of a BEC (photo reproduced with permission from American Physical Society) [49]. (e) Image of a chip–scale MOT (photo reproduced with permission from AIP publishing) [50].
2. Basic Theory of CAGS and Magneto–Optical Trap (MOT)
The working principle of a CAGS is based on the cold atom, and the preparation of a cold atom cloud (with a temperature below 10 μK) is an essential process for a CAGS. Following the atomic cooling techniques proposed by several Nobel laureates based on the Doppler effect [51][52], neutral atoms can be trapped by a magneto–optical trap (MOT) first, and then the trap uses polarization gradient cooling to further reduce the temperature of the atom cloud, so that the coherence of atoms can be further improved. With a well–prepared cold atom cloud, a three–pulse sequence (π/2–π–π/2) will be applied to split, redirect and recombine the matter–wave of cold atom clouds as a typical Mach-Zehnder interferometer as in Figure 2. The accumulated phase difference includes the free evolution phase determined by Feynman’s path integral approach, and the laser–atom interaction with gravity information contained. Through careful calculation, the gravity acceleration can be extracted from the interference fringes, obtained by scanning one of these variables, such as the chirp rate of Raman optical frequency [51].
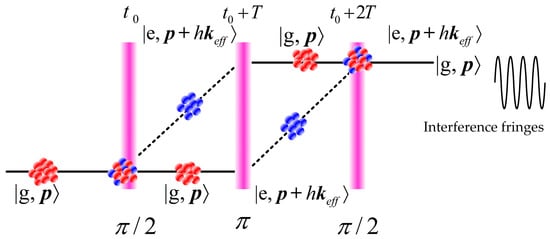
Figure 2. Pulse sequence process of an atom interferometer.
As an important component of CAGSs, the magneto–optical trap (MOT) was originally proposed and realized by Raab et al., as the most widely used method for cold atom cloud preparation [53][54][55]. The fundamental work principle of the three–dimensional MOT was realized by three pairs of circularly polarized red–detuned lasers with a static gradient magnetic field, as in Figure 3a. The static gradient magnetic field is usually around 10 G/cm, traditionally provided by a pair of anti–Helmholtz coils, and the magnetic field strength is zero at the intersection of three pairs of lasers [56]. The energy level of these atoms in the MOT will split due to the Zeeman effect, and one possible configuration of the energy level structure is as shown in Figure 3b. Researchers can set the total angular momentum of the ground state as J=0J=0, and J=1J=1 for the excited state, which contains three magneton energy levels mf=0,±1m generated by Zeeman splitting in the magnetic field. These magneton energy levels degenerate at the center of the magnetic field. Taking Z direction as an example, as in Figure 3b, two lasers collide these atoms from opposite directions. The frequency of these lasers is wLaser, the detuning frequency of which is relative to atomic resonance frequency at zero magnetic fields, or δ0. In addition, the polarization directions of these two lasers are σ+ and σ−. Due to the transition selection rules, the detuning of σ+ and σ− lasers are δ+ and δ−, respectively. Assuming the initial position of an atom is Z0 (Z0 > 0), then δ+>δ− and atoms will absorb more photons from σ− lasers, resulting in a negative centripetal force to atoms. Similarly, the atoms will gain a positive centripetal force if Z0 < 0, and all atoms will feel the radiation force from lasers pointing to the center, becoming trapped in the center as in Figure 3b.
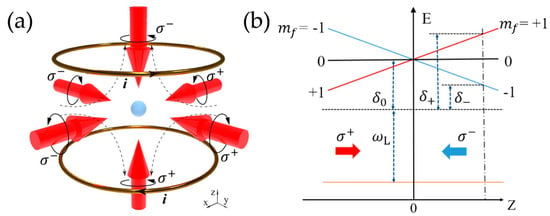
Figure 3. (a) Schematic diagram of a three–dimensional magneto–optical trap. (b) Atomic energy level splitting and trapping principle.
The traditional MOT is usually constructed by the combination of the magnetic coil and laser system, making the experimental system complicated and very heavy. Recently, with the development of integrated circuits and micro/nanofabrication processing, various designs have been proposed to simplify this system with different types of atom chips. The atom chips are usually fabricated with surface micro/nanostructures to accurately control the magnetic, electric, or light field. Using these atom chips, the confinement and coherent manipulation of cold atoms can be realized on a small scale under low power consumption conditions.
References
- Bong, K.; Holynski, M.; Vovrosh, J.; Bouyer, P.; Condon, G.; Rasel, E.; Schubert, C.; Schleich, W.P.; Roura, A. Taking atom interferometric quantum sensors from the laboratory to real-world applications. Nat. Rev. Phys. 2019, 1, 731–739.
- Rosi, G.; D’Amico, G.; Cacciapuoti, L.; Sorrentino, F.; Prevedelli, M.; Zych, M.; Brukner, C.; Tino, G.M. Quantum test of the equivalence principle for atoms in coherent superposition of internal energy states. Nat. Commun. 2017, 8, 15529.
- Sabulsky, D.O.; Dutta, I.; Hinds, E.A.; Elder, B.; Burrage, C.; Copeland, E.J. Experiment to detect dark energy forces using atom interferometry. Phys. Rev. Lett. 2019, 123, 061102.
- Burrage, C.; Copeland, E.J. Using atom interferometry to detect dark energy. Contemp. Phys. 2016, 57, 164–176.
- Wang, Y.J.; Lu, X.Y.; Qin, C.G.; Tan, Y.J.; Shao, C.G. Modeling gravitational wave detection with atom interferometry. Class. Quant. Grav. 2021, 38, 145025.
- Dimopoulos, S.; Graham, P.W.; Hogan, J.M.; Kasevich, M.A.; Rajendran, S. Gravitational wave detection with atom interferometry. Phys. Lett. B 2009, 678, 37–40.
- Rosi, G.; Cacciapuoti, L.; Sorrentino, F.; Menchetti, M.; Prevedelli, M.; Tino, G.M. Measurement of the gravity-field curvature by atom interferometry. Phys. Rev. Lett. 2015, 114, 013001.
- Mao, D.K.; Deng, X.B.; Luo, H.Q.; Xu, Y.Y.; Zhou, M.K.; Duan, X.C.; Hu, Z.K. A dual-magneto-optical-trap atom gravity gradiometer for determining the Newtonian gravitational constant. Rev. Sci. Instrum. 2021, 92, 053202.
- Sorrentino, F.; Alberti, A.; Ferrari, G.; Ivanov, V.V.; Poli, N.; Schioppo, M.; Tino, G.M. Quantum sensor for atom-surface interactions below 10 μm. Phys. Rev. A 2009, 79, 013409.
- Mohapatra, A.K.; Chaudhuri, S.; Roy, S.; Unnikrishnan, C.S. Experiments on the reflection of cold atoms from magnetic thin films—From atom optics to measurement of short-range forces. Eur. Phys. J. D 2007, 42, 287–298.
- Chang, L.B.; Qin, F.J.; Wu, M.P. Gravity disturbance compensation for inertial navigation system. IEEE Trans. Instrum. Meas. 2019, 68, 3751–3765.
- Wu, L.; Wang, H.B.; Chai, H.; Hsu, H.T.; Wang, Y. Research on the relative positions-constrained pattern matching method for underwater gravity-aided inertial navigation. J. Navig. 2015, 68, 937–950.
- Boukebbab, S.; Boulahlib, M.S. The spatial interactions using the gravity model: Application at the evaluation of transport efficiency at Constantine city, Algeria. Theory Eng. Complex Syst. Dependability 2015, 365, 35–44.
- Thompson, C.A.; Saxberg, K.; Lega, J.; Tong, D.; Brown, H.E. A cumulative gravity model for inter-urban spatial interaction at different scales. J. Transp. Geogr. 2019, 79, 102461.
- Zhu, Y.Q.; Zhan, F.B.; Zhou, J.C.; Liang, W.F.; Xu, Y.M. Gravity measurements and their variations before the 2008 Wenchuan earthquake. B. Seism. Soc. Am. 2010, 100, 2815–2824.
- Zhu, Y.; Liu, F.; You, X.; Liang, W.; Zhao, Y.; Liu, L. Earthquake prediction from China’s mobile gravity data. Geod. Geodyn. 2015, 6, 81–90.
- Xing, L.L.; Wang, L.H.; Hu, M.Z. Determination of mantle upwelling rate beneath Taiyuan basin by using absolute gravity, GPS, groundwater and GLDAS data. J. Appl. Geophys. 2017, 138, 179–184.
- Alonso, I.; Alpigiani, C.; Altschul, B.; Araujo, H.; Arduini, G.; Arlt, J.; Badurina, L.; Balaz, A.; Bandarupally, S.; Barish, B.C.; et al. Cold atoms in space: Community workshop summary and proposed road-map. Epj Quantum Technol. 2022, 9, 30.
- Freier, C.; Hauth, M.; Schkolnik, V.; Leykauf, B.; Schilling, M.; Wziontek, H.; Scherneck, H.G.; Muller, J.; Peters, A. Mobile quantum gravity sensor with unprecedented stability. In Proceedings of the 8th Symposium on Frequency Standards and Metrology 2015, Potsdam, Germany, 12–16 October 2015; Volume 723.
- Bidel, Y.; Carraz, O.; Charrière, R.; Cadoret, M.; Zahzam, N.; Bresson, A. Compact cold atom gravimeter for field applications. Appl. Phys. Lett. 2013, 102, 144107.
- Matsko, A.B.; Yu, N.; Maleki, L. Gravity field measurements using cold atoms with direct optical readout. Phys. Rev. A 2003, 67, 043819.
- Hu, Z.K.; Duan, X.C.; Zhou, M.K.; Chen, L.L. High sensitivity gravity measurements with cold atom interferometry. In Proceedings of the 2014 Conference on Lasers and Electro-Optics (CLEO)—Laser Science to Photonic Applications, San Jose, CA, USA, 8–13 June 2014.
- Kasevich, M.; Chu, S. Atomic interferometry using stimulated raman transitions. Phys. Rev. Lett. 1991, 67, 181–184.
- Wang, S.K.; Zhao, Y.; Zhuang, W.; Li, T.C.; Wu, S.Q.; Feng, J.Y.; Li, C.J. Shift evaluation of the atomic gravimeter NIM-AGRb-1 and its comparison with FG5X. Metrologia 2018, 55, 360–365.
- Gillot, P.; Francis, O.; Landragin, A.; Dos Santos, F.P.; Merlet, S. Stability comparison of two absolute gravimeters: Optical versus atomic interferometers. Metrologia 2014, 51, L15–L17.
- Karcher, R.; Imanaliev, A.; Merlet, S.; Santos, F.P.D. Improving the accuracy of atom interferometers with ultracold sources. New J. Phys. 2018, 20, 113041.
- Hu, Z.-K.; Sun, B.-L.; Duan, X.-C.; Zhou, M.-K.; Chen, L.-L.; Zhan, S.; Zhang, Q.-Z.; Luo, J. Demonstration of an ultrahigh-sensitivity atom-interferometry absolute gravimeter. Phys. Rev. A 2013, 88, 043610.
- Wang, K.N.; Xu, H.; Zhou, Y.; Xu, Y.P.; Song, W.; Tang, H.Z.; Wang, Q.W.; Zhu, D.; Weng, K.X.; Wang, H.L.; et al. Research on rapid surveying and mapping of outfield absolute gravity based on vehicle-mounted atomic gravimeter. Acta Phys. Sin. 2022, 71, 159101.
- Guo, J.; Ma, S.; Zhou, C.; Liu, J.; Wang, B.; Pan, D.; Mao, H. Vibration compensation for a vehicle-mounted atom gravimeter. IEEE Sens. J. 2022, 22, 12939–12946.
- Zhu, D.; Xu, H.; Zhou, Y.; Wu, B.; Cheng, B.; Wang, K.N.; Chen, P.J.; Gao, S.T.; Weng, K.X.; Wang, H.L.; et al. Data processing of shipborne absolute gravity measurement based on extended Kalman filter algorithm. Acta Phys. Sin. 2022, 71, 133702.
- Wu, B.; Zhao, Y.; Zhou, Y.; Yuan, P.; Zhu, D.; Cheng, B.; Wu, L.; Qiao, Z.; Wang, X.; Lin, Q. Improvement of the accuracy of ocean tide model based on the offshore continuous gravity data with atomic gravimeter. ESS Open Arch. 2023, 13, 1–14.
- Bidel, Y.; Zahzam, N.; Bresson, A.; Blanchard, C.; Cadoret, M.; Olesen, A.V.; Forsberg, R. Absolute airborne gravimetry with a cold atom sensor. J. Geod. 2020, 94, 20.
- Bonnin, A.; Bidel, Y.; Bernard, J.; Blanchard, C.; Cadoret, M.; Zahzam, N.; Schwartz, S.; Bresson, A. Marine and Airborne Gravimetry with an Absolute Cold Atom Sensor. In Proceedings of the 2022 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Avignon, France, 8–11 May 2022; pp. 1–4.
- Trimeche, A.; Battelier, B.; Becker, D.; Bertoldi, A.; Bouyer, P.; Braxmaier, C.; Charron, E.; Corgier, R.; Cornelius, M.; Douch, K.; et al. Concept study and preliminary design of a cold atom interferometer for space gravity gradiometry. Class. Quant. Grav. 2019, 36, 215004.
- Zahzam, N.; Christophe, B.; Lebat, V.; Hardy, E.; Huynh, P.A.; Marquet, N.; Blanchard, C.; Bidel, Y.; Bresson, A.; Abrykosov, P.; et al. Hybrid electrostatic-atomic accelerometer for future space gravity missions. Remote Sens. 2022, 14, 3273.
- Wu, X.J.; Pagel, Z.; Malek, B.S.; Nguyen, T.H.; Zi, F.; Scheirer, D.S.; Muller, H. Gravity surveys using a mobile atom interferometer. Sci. Adv. 2019, 5, eaax0800.
- Zhang, X.; Zhong, J.; Tang, B.; Chen, X.; Zhu, L.; Huang, P.; Wang, J.; Zhan, M. Compact portable laser system for mobile cold atom gravimeters. Appl. Opt. 2018, 57, 6545–6551.
- Peters, A.; Chung, K.Y.; Chu, S. High-precision gravity measurements using atom interferometry. Metrologia 2001, 38, 25–61.
- Chiow, S.W.; Herrmann, S.; Chu, S.; Muller, H. Noise-immune conjugate large-area atom interferometers. Phys. Rev. Lett. 2009, 103, 050402.
- Biedermann, G.W.; Wu, X.; Deslauriers, L.; Roy, S.; Mahadeswaraswamy, C.; Kasevich, M.A. Testing gravity with cold-atom interferometers. Phys. Rev. A 2015, 91, 033629.
- Gillot, P.; Cheng, B.; Imanaliev, A.; Merlet, S.; Dos Santos, F.P. The LNE-SYRTE cold atom gravimeter. In Proceedings of the 016 European Frequency and Time Forum (EFTF), York, UK, 4–7 April 2016; pp. 1–4.
- Xu, Y.Y.; Cui, J.F.; Qi, K.; Chen, L.L.; Deng, X.B.; Luo, Q.; Zhang, H.; Tan, Y.J.; Shao, C.G.; Zhou, M.K.; et al. Evaluation of the transportable atom gravimeter HUST-QG. Metrologia 2022, 59, 055001.
- Folman, R.; Kruger, P.; Schmiedmayer, J.; Denschlag, J.; Henkel, C. Microscopic atom optics: From wires to an atom chip. Adv. At. Mol. Opt. Phy. 2002, 48, 263–356.
- Weinstein, J.D.; Libbrecht, K.G. Microscopic magnetic traps for neutral atoms. Phys. Rev. A 1995, 52, 4004–4009.
- Reichel, J.; Hansell, W.; Hansch, T.W. Atomic micromanipulation with magnetic surface traps. Phys. Rev. Lett. 1999, 83, 3398–3401.
- Reichel, J. Microchip traps and Bose–Einstein condensation. Appl. Phys. B 2002, 74, 469–487.
- Hansel, W.; Hommelhoff, P.; Hansch, T.W.; Reichel, J. Bose-Einstein condensation on a microelectronic chip. Nature 2001, 413, 498–501.
- Schkolnik, V.; Hellmig, O.; Wenzlawski, A.; Grosse, J.; Kohfeldt, A.; Doringshoff, K.; Wicht, A.; Windpassinger, P.; Sengstock, K.; Braxmaier, C.; et al. A compact and robust diode laser system for atom interferometry on a sounding rocket. Appl. Phys. B 2016, 122, 217.
- Abend, S.; Gebbe, M.; Gersemann, M.; Ahlers, H.; Muntinga, H.; Giese, E.; Gaaloul, N.; Schubert, C.; Lammerzahl, C.; Ertmer, W.; et al. Atom-chip fountain gravimeter. Phys. Rev. Lett. 2016, 117, 203003.
- McGilligan, J.P.; Moore, K.R.; Dellis, A.; Martinez, G.D.; de Clercq, E.; Griffin, P.F.; Arnold, A.S.; Riis, E.; Boudot, R.; Kitching, J. Laser cooling in a chip-scale platform. Appl. Phys. Lett. 2020, 117, 054001.
- Kasevich, M.; Chu, S. Measurement of the gravitational acceleration of an atom with a light-pulse atom interferometer. Appl. Phys. B-Photo 1992, 54, 321–332.
- Phillips, W.D. Nobel Lecture: Laser cooling and trapping of neutral atoms. Rev. Mod. Phys. 1998, 70, 721–741.
- Raab, E.L.; Prentiss, M.; Cable, A.; Chu, S.; Pritchard, D.E. Trapping of neutral sodium atoms with radiation pressure. Phys. Rev. Lett. 1987, 59, 2631–2634.
- Zhang, H.K.; Wang, Y.N.; Zhu, L.X.; Li, Q.X.; Xu, D.Y.; Zhang, X.; Yan, S.H.; Yang, J. Increasing the length of free-falling path with homogeneous bias field for compact cold atom interferometers by configuring MOT coils. AIP Adv. 2020, 10, 095134.
- Wang, X.L.; Cheng, B.; Wu, B.; Wang, Z.Y.; Lin, Q. A simplified cold atom source for 3-D MOT loading. Chin. Phys. Lett. 2011, 28, 053701.
- Lin, Y.W.; Chou, H.C.; Dwivedi, P.P.; Chen, Y.C.; Yu, I.A. Using a pair of rectangular coils in the MOT for the production of cold atom clouds with large optical density. Opt. Express 2008, 16, 3753–3761.
More
Information
Subjects:
Physics, Applied; Instruments & Instrumentation
Contributors
MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register
:
View Times:
888
Revisions:
2 times
(View History)
Update Date:
07 Jun 2023
Notice
You are not a member of the advisory board for this topic. If you want to update advisory board member profile, please contact office@encyclopedia.pub.
OK
Confirm
Only members of the Encyclopedia advisory board for this topic are allowed to note entries. Would you like to become an advisory board member of the Encyclopedia?
Yes
No
${ textCharacter }/${ maxCharacter }
Submit
Cancel
Back
Comments
${ item }
|
More
No more~
There is no comment~
${ textCharacter }/${ maxCharacter }
Submit
Cancel
${ selectedItem.replyTextCharacter }/${ selectedItem.replyMaxCharacter }
Submit
Cancel
Confirm
Are you sure to Delete?
Yes
No




