Numerical Simulation Methods in Shale Oil Flow

Version	Summary	Created by	Modification	Content Size	Created at	Operation
1		Dmitriy Aleksandrovich Martyushev	--	2363	2023-05-08 08:38:47	\|
2	format	Jason Zhu	Meta information modification	2363	2023-05-09 08:43:29	\| \|
3	format	Jason Zhu	Meta information modification	2363	2023-05-10 07:55:00	\|

This entry is adapted from the peer-reviewed paper 10.3390/en16083516

The pore structure of shale oil reservoirs is complex, and the microscale and nanoscale effect is obvious in the development of shale oil reservoirs. Understanding the oil flow mechanism in shale reservoirs is essential for optimizing the development plan and enhancing the recovery rate of shale oil reservoirs.

shale oil occurrence status flow mechanism

1. Introduction

Although shale oil flow in shale pores can be studied through physical laboratory experiments to measure key parameters, such as apparent permeability, experimental studies of shale oil flow in shale pores at the microscale and nanoscale inevitably require a lot of time and the use of sophisticated and expensive experimental instruments with demanding experimental conditions and requirements, especially regarding the accuracy of the measurements. However, by studying the shale oil flow mechanism and establishing a mathematical model of shale oil flow, the shale oil flow can be simulated and studied by means of computer numerical simulation. In recent years, many scholars have studied shale oil flow via numerical simulation, and many useful conclusions have been drawn. Numerical simulation studies are divided into two major categories regarding the current shale oil flow simulations: microscopic and macroscopic. The main simulation methods for shale oil microflow are MDS, LBM, and PNM. The main simulation methods for hydraulic fracture expansion in shale reservoirs are XFEM, DDM, and DEM. A dual-porosity model couples macroscopic and microscopic flows of shale oil to simulate the shale oil production process. Based on different theoretical foundations, different simulation methods have their own scope of application, advantages, and disadvantages.

2. Shale Oil Microflow Simulation

2.1. Molecular Dynamics Simulation

MDS uses Newton’s laws of motion to simulate the trajectories of atoms or molecules in a multibody system and calculates the structure and properties of the system by statistically averaging the ensemble of its different states. For equilibrium systems, statistical averages of physical quantities can be obtained by appropriate time averaging; for non-equilibrium systems, physical phenomena occurring within a molecular dynamics observation time can be simulated. For example, Wang et al. ^[1] analyzed the molecular structure and diffusion characteristics of n-octane within the slit (pore throat diameter: 1.7–11.2 nm) using equilibrium molecular dynamics (EMD) simulations; calculated the velocity profile, fluid viscosity distribution, and slip length of n-octane within the slit (pore throat diameter: 1.7–11.2 nm) using nonequilibrium molecular dynamics (NEMD) to calculate the velocity profile, fluid viscosity distribution, and slip length within the slit; and found that the flow of octane in the middle region of the quartz nanopore tends to be bulk-liquid-like, while the diffusion is much slower in the region near the wall, and there are obvious velocity and slip changes in the flow of alkane fluid in the inorganic pore driven by external forces-induced slippage and viscosity changes.

Due to the fact that MDS can obtain many microscopic details that are not available in experiments, explain difficult experimental phenomena, and reveal the occurrence mechanism, it has been widely applied in the study of shale oil and gas flow mechanisms in recent years. MDS has demonstrated excellent roles in revealing shale oil and gas adsorption mechanisms, solid–liquid interactions and liquid-liquid interactions, and revising or establishing new transport mechanics equations. For example, Falk et al. ^[2] demonstrated that due to strong molecular adsorption, the flow of an alkane fluid in kerogen cannot be described by the conventional Darcy’s law and proposed a microscopic description of permeability based on statistical mechanics. Liu et al. ^[3] investigated the inhomogeneous distribution of the density and fraction of shale oil in the organic matter of kerogen via MDS. It was found that the heavy fraction was concentrated in bulk phase regions, and the light fraction was concentrated at the boundary layer of the wall due to the reflection effect of the wall of kerogen. The velocity distribution of the bulk phase regions showed a plug flow when the external force increased, while there was a half-parabolic distribution at the boundary layer. The velocity distribution of the bulk phase regions showed a plug flow when the external force increased, while the boundary layer showed a half-parabolic distribution.

Zhang et al. ^[4] established two mathematical models, the apparent viscosity model and the liquid–liquid slip model, based on the oil–water two-phase flow phenomena demonstrated by molecular dynamics simulations, and validated the modified mathematical models by comparing them with the results of molecular dynamics simulations and the previous models that did not consider the liquid–liquid interface phenomena.

Although the results of MDS are accurate, researchers are currently facing the following problems when using MDS: the computation is very large, and the current scale that can be simulated is very small, generally in the tens of nanometers, so it is not possible to directly simulate fluid flow in complex porous media; the credibility of MDS results mainly depends on the accuracy of the interatomic interaction potential; for rock samples with complex compositions, it is also a challenging topic to build more accurate whole-molecule models of shale oil and molecular structures that are closer to that of kerogen.

2.2. Lattice Boltzmann Method

LBM is a mesoscopic approach between the microscopic (molecular) and macroscopic (continuum) scales, which can easily handle fluid flow in complex structures and is becoming an effective tool for simulating fluid flow in porous media. Through parallel computation and algorithm simplification, it is able to reduce computational resources to a large extent. M.P. Lautenschlaeger et al. ^[5] proposed a simple and effective LBM that is particularly suitable for non-homogeneous porous media with good numerical stability and has many application scenarios, including, of course, shale oil–water flow. LBM is a direct numerical simulation method, using MDS to obtain microscopic parameters such as the velocity/density distribution of shale oil in organic or inorganic nanopores, fitting velocity/density distribution through LBM single nanopore simulation to obtain lattice parameters such as slip length and solid–liquid interaction force, and finally extending single nanopore shale oil flow to complex porous media flow based on this fitted lattice parameter to further study the influence mechanism of complex parameters such as non-homogeneous wetting and pore geometry on apparent permeability ^[6]^[7]^[8]. For example, Zhang et al. ^[9] introduced the interaction between water molecules and solid walls into the LBM equation and proposed a mesoscopic LBM to capture the density distribution and velocity distribution of water flowing in nanopore channels.

Similarly, Zhao et al. ^[10] expressed the molecular interaction between water and solid walls in terms of real and apparent slip, and by fitting a large number of numerical simulation results of LBM, a nanopore water flow model with different cross-sectional shapes was established and expressed as the following empirical equation, which is easily applicable for widespread use in engineering.

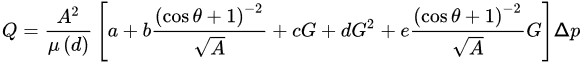
Where the coefficients

a - e

denote empirical constants ^[10];

Q

is the flow rate;

A

is the cross-sectional surface area;

Δ p

represents the pressure drop;

G

is the shape factor;

θ

indicates the contact angle; and

μ (d)

is the effective viscosity, i.e., a constant in a water–nanopore system with a specific dimension.

At present, most scholars use LBM to study the flow law of water in nanoporous media, and the proposed model can also be used to study the flow of shale oil in nanoporous media. The key points to account for when using LBM to study shale oil and gas flow ^[11] are how to accurately consider the solid–liquid interaction and liquid–liquid interaction, how to consider the wall roughness, the development of new wall boundary treatment methods, and the introduction of new wall force models, etc.

2.3. Pore Network Model

A PNM abstracts the rock as a network consisting of large spatial pores and narrow spatial pore throats, which are the smallest computational units in the simulation of the rock flow process ^[12]^[13]. The advantage of a pore network is that it can reflect the geometric topology and connectivity of the core in a more realistic way. The pore space is only used as a storage space during the calculation, and the flow and pressure in the pore throat can be calculated directly by applying existing mechanical laws without simulating the details of body flow; so, the calculation is very efficient compared to LBM and suitable for studying the shale oil flow mechanism at the microscale ^[14]. Based on the modified shale oil flow equation, Yang et al. ^[15] established a new PNM to investigate the effects of slip length and the adsorption effects on shale oil permeability and found that shale oil flow is mainly controlled by inorganic pores at low TOC, while the connectivity between organic pore throats is improved with increasing organic matter content. In recent years, traditional PNMs have used ball-and-stick models without considering the characteristics of the true pore structure, and a fast and accurate calculation method has been established by combining the PNM with direct simulation. Zhao et al. ^[16] found that the accuracy of the computational model is inversely proportional to the computational speed by comparing three sets of numerical simulations of single-phase fluids in porous media. They concluded that, in order to obtain an efficient and accurate model, it is a good choice to first simplify the real pore network to some extent and then compute it by LBM, and this method was called the improved pore network model (IPNM).

There is nothing special in the calculation method of PNM. PNM can be calculated by applying the existing laws of mechanics, and whether it is properly applied depends mainly on the construction of the pore network. In recent years, especially with the popularization and application of FIB/SEM technology, it has become a trend to build a more seamless pore network, so the construction of the pore network from core microscopic images has caused PNM to be more widely used ^[17]. Adding structural features, mineral components, and surface structural properties of rock samples into the pore network is a problem to be considered by PNM. In fact, PNM can be used as an effective tool to upscale MD (or LBM) results. PNM can reflect the basic characteristics and connectivity of rock structure but can also easily integrate MD (or LBM) results into it, and at the same time, PNM is computationally efficient compared with the other two methods, which facilitates a larger range of flow simulation calculations.

3. Shale Oil Microflow and Macroflow Coupling Model

In recent years, the development of hydraulic fracturing and horizontal well drilling technologies has made it possible to commercially exploit shale oil and gas resources endowed in low permeability rocks. From the previous part, shale oil flows in nanoscale pores in the shale matrix subject to many micromechanical behaviors that result in the flow of shale oil in nanopores that cannot be described by the conventional Darcy’s law. However, fractures formed by hydraulic fracturing reach the millimeter level, and compared to the flow of shale oil and gas in the shale matrix, it is believed that the flow of shale oil in artificial hydraulic fractures belongs to the macroscopic flow of shale oil and the microscopic effects can be neglected, so the flow can be described by Darcy’s law.

There are many studies on shale oil microflow and macroflow mechanisms, and researchers have developed their own theoretical models. Coupling shale oil microflow and macroflow is crucial for shale reservoir development.

Where $K_{1}$ , $K_{2}$ is the permeability tensor of the two media; and $f_{1}$ , $f_{2}$ is the proportion of the two media, $(f_{1} + f_{2} = 1)$ .

If the permeability of the medium is a scalar, it is obtained from Equation—

K_{x x} = K_{1} K_{2} / (f_{1} K_{2} + f_{2} K_{1})

K_{x y} = K_{y x} = 0

K_{y y} = f_{1} K_{1} + f_{2} K_{2}

—i.e., the equivalent permeability is a harmonic average in the x-direction and an arithmetic average in the y-direction. This approach to dealing with permeability inhomogeneities acts as a guide for the coupling microscopic and macroscopic flows in shale oil ^[18]. If one considers the flow of shale oil in matrix and hydraulic fractures as flow in two porous materials with different permeabilities, then averaging these two different permeabilities in a certain way (harmonic average, arithmetic average, geometric average, etc.), will yield a “rough permeability” that can be applied in engineering. However, the hydraulic fracture orientation is very complex in production practice, and it is difficult to use large-scale averaging under such conditions. Moreover, this method is not accurate in simulating multiphase flow ^[19].

The microscopic flow mechanism of shale oil has been elucidated in the above section, which mainly includes adsorption, resolution and diffusion, etc., specifically in terms of density/velocity inhomogeneity, and the corresponding mathematical model can be established; the flow of shale oil in hydraulic fractures follows Darcy’s law; the oil reservoir also changes during the extraction process, following the rock equation of state; reservoir permeability changes and pressure changes, etc., can also be taken into account. The model then sets the same flow rate or pressure at the boundary of different media, thus coupling the above-mentioned multiscale flow in the reservoir development process, and the established mathematical model is solved numerically to realize the dynamic simulation of the reservoir development process. Su et al. ^[20] established a dual-porosity model to explain the quasi-steady cross-flow between fracture and matrix consisting of viscous flow and the steady adsorption and desorption process. Zhang et al. ^[21] used fractal theory to describe the stimulated reservoir volume (SRV) in order to characterize the complex fracture network structure after hydraulic fracturing, and coupled fractal relations with a dual-porosity model to establish a new semi-analytical model for simulating the effectively stimulated volume of fractured wells in tight reservoirs, which simulates the flow of shale oil in the fracture-modified reservoirs.

At present, the characterization of the fracture network is still relatively simple in most of the studies, and the complex fracture network structure is usually replaced by a few straight lines, which is obviously not accurate enough. Many previous studies on the formation of the fracture network of hydraulic fracturing have been conducted, and there are various numerical simulation methods (such as XFEM, DDM, and DEM, etc.), that can simulate the expansion of hydraulic fracturing under specific conditions. However, it is difficult to solve the coupled model under the complex fracture network, and solving the dual-porosity model while considering multiple micromechanical behaviors under the macroscopic complex fracture network is also a major difficulty in the research.

References

Wang, S.; Javadpour, F.; Feng, Q. Molecular dynamics simulations of oil transport through inorganic nanopores in shale. Fuel 2016, 171, 74–86.
Falk, K.; Coasne, B.; Pellenq, R.; Ulm, F.-J.; Bocquet, L. Subcontinuum mass transport of condensed hydrocarbons in nanoporous media. Nat. Commun. 2015, 6, 6949.
Liu, J.; Yang, Y.; Sun, S.; Yao, J.; Kou, J. Flow behaviors of shale oil in kerogen slit by molecular dynamics simulation. Chem. Eng. J. 2022, 434, 134682.
Zhang, W.; Feng, Q.; Wang, S.; Zhang, X.; Zhang, J.; Cao, X. Molecular Simulation Study and Analytical Model for Oil–Water Two-Phase Fluid Transport in Shale Inorganic Nanopores. Energies 2022, 15, 2521.
Lautenschlaeger, M.P.; Weinmiller, J.; Kellers, B.; Danner, T.; Latz, A. Homogenized lattice Boltzmann model for simulating multi-phase flows in heterogeneous porous media. Adv. Water Resour. 2022, 170, 104320.
Li, Z.-Z.; Min, T.; Kang, Q.; He, Y.-L.; Tao, W.-Q. Investigation of methane adsorption and its effect on gas transport in shale matrix through microscale and mesoscale simulations. Int. J. Heat Mass Transf. 2016, 98, 675–686.
Takbiri-Borujeni, A.; Fathi, E.; Kazemi, M.; Belyadi, F. An integrated multiscale model for gas storage and transport in shale reservoirs. Fuel 2019, 237, 1228–1243.
Wang, H.; Wang, W.D.; Su, Y.L.; Jin, Z.H. Lattice Boltzmann Model for Oil/Water Two- Phase Flow in Nanoporous Media Considering Heterogeneous Viscosity, Liquid/Solid, and Liquid/Liquid Slip. SPE J. 2022, 27, 3508–3524.
Zhang, T.; Javadpour, F.; Li, X.; Wu, K.; Li, J.; Yin, Y. Mesoscopic method to study water flow in nanochannels with different wettability. Phys. Rev. E 2020, 102, 013306.
Zhao, W.; Jia, C.; Zhang, T.; Jiang, L.; Li, X.; Jiang, Z.; Zhang, F. Effects of nanopore geometry on confined water flow: A view of lattice Boltzmann simulation. Chem. Eng. Sci. 2021, 230, 116183.
Zachariah, G.T.; Panda, D.; Surasani, V.K. Lattice Boltzmann simulations for invasion patterns during drying of capillary porous media. Chem. Eng. Sci. 2019, 196, 310–323.
Cui, R.; Feng, Q.; Chen, H.; Zhang, W.; Wang, S. Multiscale random pore network modeling of oil-water two-phase slip flow in shale matrix. J. Pet. Sci. Eng. 2019, 175, 46–59.
Wang, X.; Zhang, Z.; Gong, R.; Wang, S. Pore Network Modeling of Oil–Water Flow in Jimsar Shale Oil Reservoir. Front. Earth Sci. 2021, 9, 738545.
Lin, M.; Jiang, W.B.; Li, Y.; Yi, Z.X.; Zhang, Z.B. Several Questions in the Micro-Scale Flow of Shale Oil/Gas. Bull. Mineral. Petrol. Geochem. 2015, 34, 18–28.
Yang, Y.; Wang, K.; Zhang, L.; Sun, H.; Zhang, K.; Ma, J. Pore-scale simulation of shale oil flow based on pore network model. Fuel 2019, 251, 683–692.
Zhao, J.; Qin, F.; Derome, D.; Kang, Q.; Carmeliet, J. Improved pore network models to simulate single-phase flow in porous media by coupling with lattice Boltzmann method. Adv. Water Resour. 2020, 145, 103738.
Song, W.H.; Liu, L.; Sun, H.; Zhang, K.; Yang, Y.F.; Yao, J. Pore structure characterization and flow ability of shale oil reservoir based on digital cores. Pet. Reserv. Eval. Dev. 2021, 11, 497–505.
Mabiala, B.; Nsongo, T.; Tomodiatounga, D.N.; Tathy, C.; Nganga, D. Two-Dimensional Modeling of the NAPL Dissolution in Porous Media: Heterogeneities Effects on the Large Scale Permeabilities and Mass Exchange Coefficient. Comput. Water Energy Environ. Eng. 2017, 6, 56–78.
Wei, P.Y.; Shi, A.F.; Wang, X.H.; Zhou, F.Q. A Discrete Fracture-Dual Porosity Coupling Model for Shale Gas Reservoirs. Chin. Q. Mech. 2015, 36, 179–188.
Su, Y.; Zhang, Q.; Wang, W.; Sheng, G. Performance analysis of a composite dual-porosity model in multi-scale fractured shale reservoir. J. Nat. Gas Sci. Eng. 2015, 26, 1107–1118.
Zhang, Q.; Su, Y.; Wang, W.; Sheng, G. A new semi-analytical model for simulating the effectively stimulated volume of fractured wells in tight reservoirs. J. Nat. Gas Sci. Eng. 2015, 27, 1834–1845.

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.

Upload a video for this entry

Information

Subjects: Geology

Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :

Zhiyu Li

Zhengdong Lei

Weijun Shen

Dmitriy A. Martyushev

Xinhai Hu

View Times: 270

Update Date: 10 May 2023

Table of Contents

Video Upload Options

Confirm