Loosening and Preload Loss of Threaded Connections

Version	Summary	Created by	Modification	Content Size	Created at	Operation
1		Muhammad Hassaan Bin Tariq	--	2602	2023-02-13 12:17:16	\|
2	format correct	Conner Chen	Meta information modification	2602	2023-02-14 04:41:25	\|

This entry is adapted from the peer-reviewed paper 10.3390/machines11020212

Threaded fasteners are vastly used in the industry due to ease of mounting and dismounting and flexibility of design. Nonetheless, several researchers indicate that most failures recorded on nearly any kind of machinery and vehicles are initiated at fasteners. Loosening is a process of rotation of the bolt in a direction opposite to the tightening. This can cause a loss of preload (tension created in the screw shank upon tightening) which can cause failures in the machinery.

Threaded fasteners Self-loosening failure Preload loss

1. Loosening and Preload Loss (Dynamic or Static)

Loosening is a process of rotation of the bolt in a direction opposite to the tightening. This can cause a loss of preload (tension created in the screw shank upon tightening) which can cause failures in the machinery ^[1]. For instance, Olmi ^[2] investigated the crack generated in a geartrain housing of an asphalt milling machine. The experimental simulation of the entire process with the assembly and the possible external loads showed that there was a stress increase due to the load hysteresis. The stress peak was present especially at the curvature where the crack originated. This load hysteresis was made possible due to the vibrational loading by the engine, which resulted in the self-loosening of the bolts. Therefore, he suggested design improvements along with the use of dampers to prevent the vibrational loading generated by the engine. Another preload loss due to dynamic loading and reported in the literature occurred in a pinion shaft for wheel loaders ^[2]. Croccolo et al. ^[3] investigated the fracture of the pinion shaft at its threaded end. A ring nut was used to preload the angular roller bearings. It was shown that the preload loss that took place under the nominal duty cycle is around 15 kN, due to which loosening starts occurring. This loosening results in the crack of the weakest portion of the assembly, i.e., the root of a sharp notch next to the threaded portion where the ring nut engages. The suggestion for maintaining the preload given was to use either an adhesive threadlocker or a mechanical locking device. Otherwise, the design of the assembly should be altered to lessen the amount of the loading, which includes using more compliant sleeves or even removing the inner sleeve ^[3].

Preload loss of threaded fasteners is also affected by the types of materials in use. For instance, Den Otter and Maljaars ^[4] reported that when stainless-steel bolts are used in aluminium-plated slip-resistant connections, significantly greater preload loss is observed as compared to the carbon steel bolts as specified in ISO 898-1. This preload loss is due to several reasons, among which viscoplastic behaviour, plate contraction and drop in the temperature are mentioned by the authors. The viscoplastic behaviour includes creep and relaxation phenomena. Therefore, it was suggested to use a higher safety factor (1.3–1.5 instead of 1.25 provided in EN 1999-1-1) depending on connection configuration to compensate for the increased preload loss due to material combination in the ultimate limit state ^[4]. It is worth remarking that a higher factor of safety determines an increase in the weight and cost of the engineering structure ^[5]. Therefore, if these aspects are crucial, the safety factor should be minimized by taking into account all the available information such as thread friction, rough surface finishing and the actual distance between the bolt axis and the edge of members ^[6].

Moreover, the initial preload application can also affect the loosening of the bolted connections. Bhattacharya et al. ^[7] studied the effects of initial preload application on M16 steel bolts that loosening is minimum when the initial preload is greater than or equal to 12 kN, as shown in Table 1. This might be due to the pronounced deformation of the points of contact with greater force values, which enable them to offer more friction ^[7].

Table 1. Loss of preload affected using different amounts of initial preload application for M16 steel bolt ^[7].

Initial Clamping Force (kN)	Percentage of Loosening
8	16
9	6.4
10	6.0
11	5.9
12	3.4
13	3.0
14	2.5
15	2.5
16	2.7
17	3.0
18	3.6

2. Theories of Loosening Process

Various theories have been put forward to explain the process of loosening. The first theory on the rotation mechanism in bolts was coined by Sakai ^[8] in 1978. He reported that loosening occurs when the torque for bolt underhead slip is greater than the loosening torque for thread surface slip and lesser than the tightening torque required by the threaded portion. It was assumed in the theory that the nut is fixed; hence, the condition for loosening was based only on the torques on the bolt surfaces. In the classical theory used by Junker ^[9] (also known as the “complete slippage theory”), loosening is said to occur when frictional forces on the threaded surfaces are completely overcome. Yamamoto and Kasei ^[10] proposed a two-stage theory, where the first stage represents slippage on bolt-nut thread surfaces producing torsion on the bolt shank. In the second stage, the rotation of the bearing surface occurs on a moving plate, which results in a release of torsional deformation and produces loosening. In Junker’s theory, the bolt loosens first; however, in Yamamoto’s theory, the nut loosens first ^[10]. In contrast to the classical theory, Pai and Hess ^[11] proposed the “local slippage accumulation theory”. According to such a theory, complete slippage is not necessary to initiate loosening. Loosening starts when local areas of slippage accumulate together over the number of vibration cycles. Recently Li et al. ^[12] extended Sakai’s theory of self-loosening to include free nuts and free bolts under rotary vibrational loading, which agreed well with the experimental evidence. According to their theory, local slippage does not account for loosening, as opposed to the Pai and Hess theory. In Pai and Hess’s theory, the transverse load can introduce eccentricity, which in turn allows the piling up of local slippage. However, Li et al. ^[12] introduced a theory for rotational loading in which there is no eccentricity and hence does not allow accumulation of local slippage. These theories are summarised in Table 2.

Table 2. Theories of loosening mechanisms presented by different researchers.

Theory	Reference
Sakai’s fixed nut and free bolt head theory	^[8]
Junker’s complete slippage theory	^[9]
Two-stage theory by Yamamoto and Kasei	^[10]
Local slippage theory	^[11]
Theory for rotational loading	^[12]

3. Analytical Modelling

Loss of preload can occur with or without external excitation. This phenomenon of loss of preload has been studied from both standpoints in the past. Bretl and Cook ^[13] performed a static numerical analysis of the loading distribution over the threads during bolt tightening. Moreover, for the calculation of thread force, Miller et al. ^[14] established an equivalent spring model for fastening of the bolt and the nut. This approach is relatively simple and immediate. Miller’s model was later improved by Daadbin ^[15] by adding stiffness and damping, which he claimed to be influential factors for load transmission. Further investigation into the problem was performed by Daadbin and Chow ^[16], who examined the impact of the loading scheme on the preload loss. However, they neglected the deformation of the thread and modelled only one thread, because of which their model was unrealistic. Nevertheless, they concluded that the preload loss is less for the fine pitch, as it leads to a greater coefficient of friction and duration of applied force ^[16]. Moreover, an exponential expression for the stiffness of the members of bolted connections was developed using the numerical modelling by Wileman et al. ^[6]. Additionally, Chen et al. ^[17] made a significant improvement in Miller’s model by considering a multiple-thread system and adding the threads and bolt shank deformations. They modelled both the static and dynamic loading of the bolts and also determined if the bolt is exceeding the elastic limit by excessive initial preload. They calculated the effects of various aspects including the lead angle, material type, and external excitation parameters using the developed models. They concluded that a larger preload results in the extended service life of a bolted connection, whereas the trend is opposite for the lead angle of the threads and frequency of excitation force. They demonstrated the use of the model in the optimization of the design of a missile tail wing. Using the model, it was shown that preload loss, e.g., was decreased by decreasing the lead angle of the threads ^[17].

The various kind of loadings on the bolted joints can result in the loosening of the bolted joints. Work has been done to study the loosening process under different loading conditions such as axial, transverse, rotational vibration, impact loading and thermal loadings.

2.1 A. Vibrational Loading

The majority of the vibrational loading on the threaded fasteners results in the loosening phenomenon. As an example, Casanova ^[18] studied the fracture of bolts joining the draft tube of a Francis turbine. The failure originated due to the presence of extremely high vibrational loading. The assembly failed in fatigue due to the loosening of the bolts connecting the draft tube with the lower flange. The preload loss characteristics of bolts must be increased, or the lower assembly should be designed such that preload loss is prevented in the bolts working under conditions of vibrational loading ^[18].

Housari and Nassar ^[19]^[20] developed a linear mathematical model to represent the self-loosening behaviour of bolts subjected to transverse vibrational excitation and validated it experimentally. Later, Yang and Nassar ^[21]^[22] developed more accurate, non-linear models for representing the bolt self-loosening subjected to transverse vibrational excitation. In their models, they considered the beam-bending equations to evaluate the bolt deflection and angle of rotation in a direction opposite to the tightening when it is subjected to external excitation. They considered a non-linear pressure distribution under the bolt head and on the thread surface, yet neglected the effect of nut threads ^[21]^[22]. Recently, Nassar and Yang ^[23] improved the same mathematical model to encompass the effect of the nut-thread geometry in the thread-friction analysis of the bolt–nut system, which came out to be in good agreement with the experimental results. However, analytical modelling still requires many parameters, such as the plasticity of the threads, to be taken into account for a realistic approach, which makes it much more computationally expensive ^[24]. Therefore, many researchers have studied the loosening response of bolted joints subjected to vibration experimentally as well as numerically.

Experimentally, Goodier and Sweeney ^[25] studied the axial vibrational loading in 1945 at Cornell University using microscopes to measure the nut rotations. Following their experimentation, different researchers improved their apparatus and studied the effects of various parameters on the loosening ^[26]^[27]. In 1969, an apparatus for the application of vibrational loading to the bolted connections was developed by Junker ^[9], which opened a new phase of research in the loosening of bolted connections. Junker used an eccentric mechanism to apply the vibrational loading to the bolted connection connections, the basic mechanism of which is shown in Figure 1.

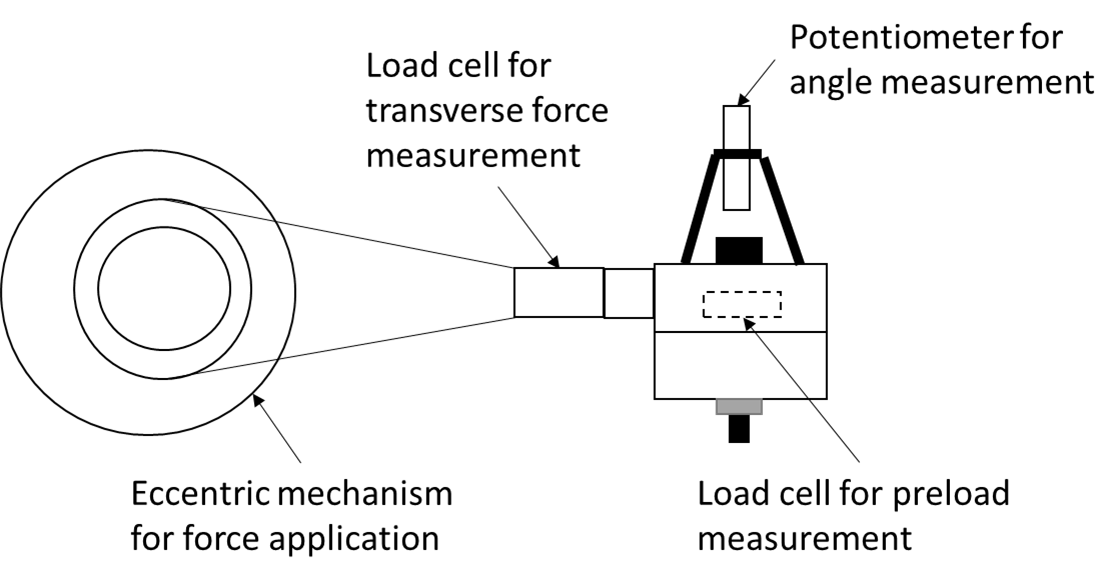
Figure 1. Schematic diagram of Junker apparatus used to apply vibrational loading to the bolted connections.

His apparatus is still used by researchers with some modifications ^[20]^[28] and it also laid the foundations for current standardized testing of fasteners against vibrational loosening ^[29]. Another German engineer, Dinger ^[30], developed a more sophisticated machine for applying transverse and rotational vibrational excitations to bolted connections. Using his apparatus, the combined loading of translation and rotation can also be applied to the bolted connection. It has been found that self-loosening could occur below the critical kinematic parameters used in pure rotational or pure translational loading.

Dinger ^[31] also used a complete FEA model, whose working principle is shown in Figure 2, to replicate the bolt loosening phenomenon. He used the local slippage theory to find out the critical condition for the rotational loosening. The results of FEA were in agreement with the experimental analysis performed.

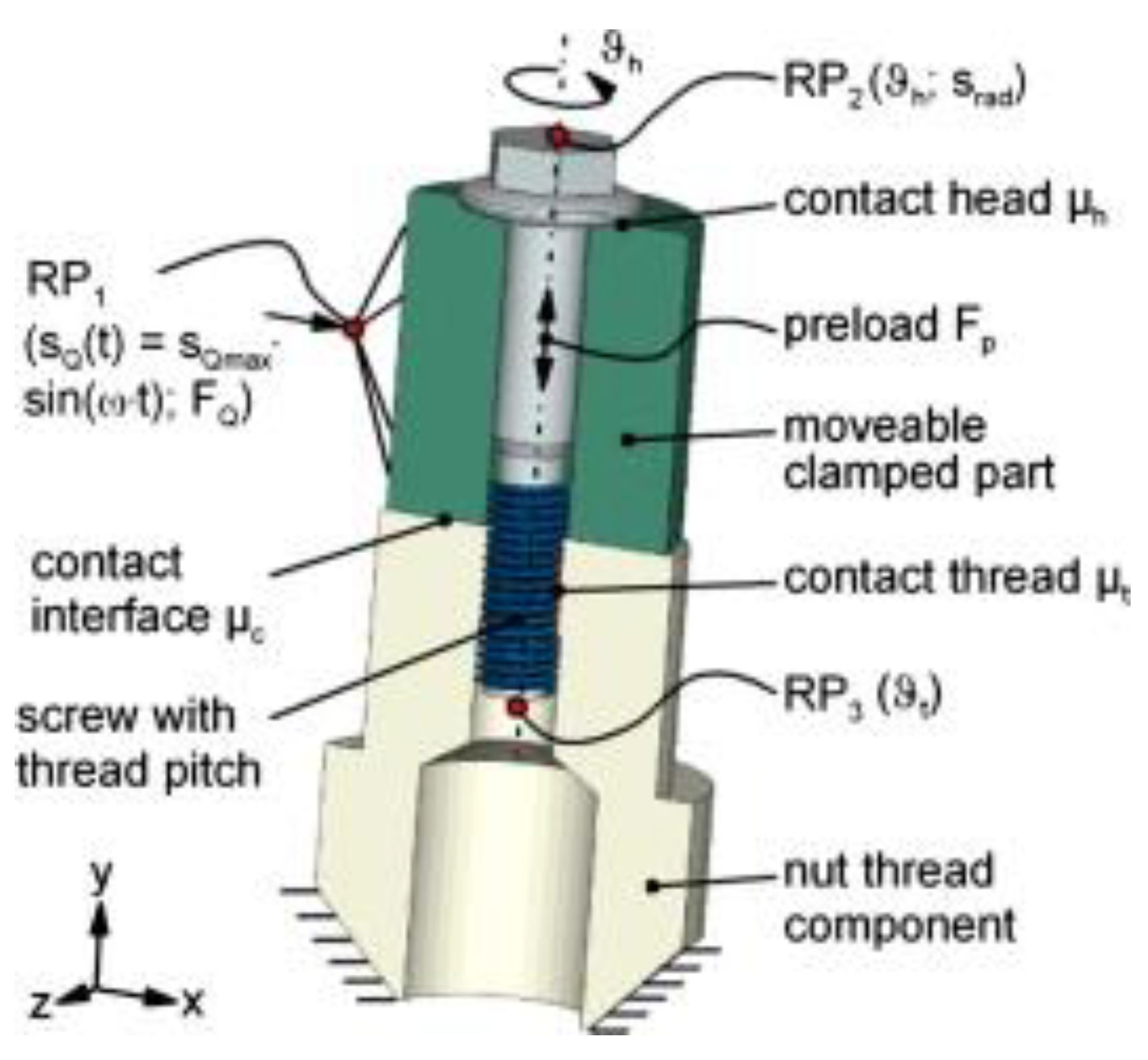
Figure 2. Finite element model of the bolted connection using the localized slippage theory ^[31].

Chen et al. ^[32] performed FEA for studying the behaviour of the bolts subjected to transverse cyclic loading. The authors concluded from the simulations for tightening and loosening that a creep slip phenomenon is present, which permits the loosening of the bolt even with some of the stuck contact facets.

Moreover, in order to study the loosening response towards random vibration in PCB bolts, Du et al. ^[33] developed an experimental configuration to provide triaxial random vibrations using a triaxial vibrostand as shown in Figure 3. The base of the setup is fixed, denoted by position 5, and the PCB (position 4) is mounted on the base. Positions 3, 6, 7 and 8 correspond to triaxial accelerometers. Positions 2 and 9 are relevant to strain rosettes, and position 1 refers to the M10 UNC thread bolt. The authors also performed FE analyses for random vibrations and found a good agreement between the experimentation and the analysis. On the basis of their analysis, they proposed a three-stage criterium (stable, transition, loosen stages) for the self-loosening of the randomly vibrating specimen ^[33].

Figure 3. Experimental apparatus for random vibration of the bolted connections ^[33].

Table 3 enlists the various mathematical models as well as experimental techniques used to investigate the self-loosening phenomenon.

Table 3. Review of literature on self-loosening due to vibrational loading.

Mathematical Models	Reference
Linear self-loosening mathematical model	^[19]^[20]
Non-linear self-loosening mathematical model	^[21]^[22]
Incorporation of nut thread effect in a non-linear self-loosening model	^[23]
Experimental Analysis	Reference
Use of microscopes to measure nut rotation	^[25]
Junker’s apparatus for transverse excitation	^[9]
Dinger’s apparatus for transverse and rotational excitation	^[30]
Experimental configuration for PCB subjected to random vibrations	^[33]

2.2. B. Impact Loading

Similarly, impact testing experimentation was performed initially by Baubles et al. ^[34]. They applied vibrations at excitation frequencies of 30 Hz and 60 Hz to the fixture, by means of a universal fatigue testing machine and electromagnetic shaker, respectively. Zhang et al. ^[35] developed an experimental apparatus to evaluate the effects of clamp length and loading direction of bolted joints on their self-loosening behaviour. The apparatus consists of a load cell for the measurement of clamp force, an angle transducer which measures the rotation of the screw tip, and an extensometer, which picks up the axial displacement of the joint. The line of action of the force was kept along the contact surfaces of the two plates in order to prevent any undesired bending moments coincident with the line of action of the screw force. Pin joints were used to attach the movable and fixed plates to the two jaws of the universal testing machine, which enabled easy force calculations.

2.3. C. Thermal Loading

Miller et al. ^[36] performed experimental and numerical investigation on bolts applied to a c-beam structure. They used a shaker with an amplifier for applying an external excitation to the c-beam structure. Eraliev et al. ^[37] developed an experimental setup to study the loosening behaviour of bolted connections under temperature changes. To study the phenomenon, they used two steel plates of 30 mm thickness. For preload change measurement, they used a washer-type compression load cell, while the temperature was monitored by means of a K-type thermocouple. A laser sensor was used to measure the movement of a thin plate attached to the nut, thus calculating the rotation of the nut. Heat cartridges as shown in Figure 4 were used to heat up the specimen. They found a direct proportionality between temperature increment and bolt preload loss, with preload being greater in the 1st cycle as compared to the remaining cycles.

Figure 4. Experimental setup to study self-loosening due to temperature changes ^[37].

All the examples above indicate that the phenomenon of loosening must be considered by engineers for designing a bolted connection with a particular focus on the type of loading, materials and temperature changes that can occur. Moreover, it can be deduced that self-loosening plays a crucial role in the failure of threaded connections. This phenomenon is attributable to different causes and requires adequate predictive modelling. Specifically, the literature review highlights the need for analytical modelling for rotational loosening as well as for local slippage accumulation in case of transverse excitation. Moreover, extensive research should be dedicated to investigating the role of material combinations in loosening.

References

Pai, N.G. Vibration Induced Loosening of Threaded Fasteners: Mechanisms, Modeling and Design Guidelines. University of South Florida: Tampa, FL, USA, 2002.
Olmi, G. An experimental investigation on a crack propagating from a geartrain housing in an asphalt milling machine. Eng. Fail. Anal. 2014, 38, 38–48.
Croccolo, D.; De Agostinis, M.; Fini, S.; Olmi, G. A numerical and experimental approach to the design and failure analysis of a pinion shaft for wheel loaders. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 1493–1504.
Otter, C.D.; Maljaars, J. Preload loss of stainless steel bolts in aluminium plated slip resistant connections. Thin-Walled Struct. 2020, 157, 106984.
Kharmanda, G.; Olhoff, N.; El-Hami, A. Optimum values of structural safety factors for a predefined reliability level with extension to multiple limit states. Struct. Multidiscip. Optim. 2004, 27, 421–434.
Wileman, J.; Choudhury, M.; Green, I. Computation of Member Stiffness in Bolted Connections. J. Mech. Des. Trans. ASME 1991, 113, 432–437.
Bhattacharya, A.; Sen, A.; Das, S. An investigation on the anti-loosening characteristics of threaded fasteners under vibratory conditions. Mech. Mach. Theory 2010, 45, 1215–1225.
Sakai, T. Investigations of bolt loosening mechanisms. Bull. JSME 1978, 21, 1391–1394. Available online: http://www.mendeley.com/research/geology-volcanic-history-eruptive-style-yakedake-volcano-group-central-japan/ (accessed on 15 December 2022).
Junker, G.H. New Criteria for Self-Loosening of Fasteners Under Vibration. SAE Tech. Pap. 1969, 78, 314–335.
Yamamoto, A.; Kasei, S. Investigation on the self loosening of threaded fasteners under transverse vibration-A solution for self-loosening mechanism. J. Jpn. Soc. Precis. Eng. 1977, 43, 470–475.
Pai, N.; Hess, D. Three-dimensional finite element analysis of threaded fastener loosening due to dynamic shear load. Eng. Fail. Anal. 2002, 9, 383–402.
Li, Z.; Chen, Y.; Sun, W.; Jiang, P.; Pan, J.; Guan, Z. Study on self-loosening mechanism of bolted joint under rotational vibration. Tribol. Int. 2021, 161, 107074.
Bretl, J.L.; Cook, R.D. Modelling the load transfer in threaded connections by the finite element method. Int. J. Numer. Methods Eng. 1979, 14, 1359–1377.
Miller, D.L.; Marshek, K.M.; Naji, M.R. Determination of load distribution in a threaded connection. Mech. Mach. Theory 1983, 18, 421–430.
Daadbin, A. Static and dyamic analysis of knuckle shape threaded joints. Mech. Mach. Theory 1990, 25, 225–232.
Daadbin, A.; Chow, Y. A theoretical model to study thread loosening. Mech. Mach. Theory 1992, 27, 69–74.
Chen, J.-H.; Hsieh, S.-C.; Lee, A.-C. The failure of threaded fasteners due to vibration. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2005, 219, 299–314.
Casanova, F. Failure analysis of the draft tube connecting bolts of a Francis-type hydroelectric power plant. Eng. Fail. Anal. 2009, 16, 2202–2208.
Nassar, S.A.; Housari, B.A. Effect of Thread Pitch and Initial Tension on the Self-Loosening of Threaded Fasteners. J. Press. Vessel. Technol. Trans. ASME 2005, 128, 590–598.
Housari, B.A.; Nassar, S.A. Effect of Thread and Bearing Friction Coefficients on the Vibration-Induced Loosening of Threaded Fasteners. J. Vib. Acoust. Trans. ASME 2007, 129, 484–494.
Yang, X.; Nassar, S. Analytical and Experimental Investigation of Self-Loosening of Preloaded Cap Screw Fasteners. J. Vib. Acoust. 2011, 133, 031007.
Nassar, S.A.; Yang, X. A Mathematical Model for Vibration-Induced Loosening of Preloaded Threaded Fasteners. J. Vib. Acoust. Trans. ASME 2009, 131, 021009.
Nassar, S.A.; Yang, X. Modeling the effect of nut thread profile angle on the vibration-induced loosening of bolted joint systems. In Advanced Joining Processes; Öchsner, A., da Silva, L.F.M., Altenbach, H., Eds.; Elsevier Inc.: Amsterdam, The Netherlands, 2020; pp. 29–54.
Liu, Z.; Wang, B.; Li, Y.; Zhang, C.; Wang, Y.; Chu, H. Analysis of self-loosening behavior of high strength bolts based on accurate thread modeling. Eng. Fail. Anal. 2021, 127, 105541.
Goodier, J.N. Loosening by Vibration of Threaded Fastenings. Mech. Eng. 1945, 67, 798.
Sauer, J.A.; Lemmon, D.C.; Lynn, E.K. Bolts: How to prevent their loosening. Mach. Des. 1950, 22, 133–139.
Paland, E.G. Investigation of the Locking Features of Dynamically Loaded Bolted Connections. Doctoral Dissertation, Hannover University, Hannover, Germany, 1966.
Zaki, A.M.; Nassar, S.A.; Yang, X. Effect of Conical Angle and Thread Pitch on the Self-Loosening Performance of Preloaded Countersunk-Head Bolts. J. Press. Vessel. Technol. Trans. ASME 2012, 134, 021210.
DIN 65151:2002-08; Aerospace Series—Dynamic Testing of the Locking Characteristics of Fasteners under Transverse Loading Conditions (Vibration Test). Deutsche Institut für Normung E.V. (DIN): Berlin, Germany, 2002.
Dinger, G. Design of multi-bolted joints to prevent self-loosening failure. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 230, 2564–2578.
Dinger, G. and Friedrich, G. Avoiding self-loosening failure of bolted joints with numerical assessment of local contact state. Eng. Fail. Anal. 2011, 18, 2188–2200.
Chen, Y.; Gao, Q.; Guan, Z. Self-Loosening Failure Analysis of Bolt Joints under Vibration considering the Tightening Process. Shock. Vib. 2017, 2017, 2038421.
Du, J.; Qiu, Y.; Wang, Z.; Li, J.; Wang, H.; Wang, Z.; Zhang, J. A three-stage criterion to reveal the bolt self-loosening mechanism under random vibration by strain detection. Eng. Fail. Anal. 2022, 133, 105954.
Baubles, R.C.; Mccormick, G.J.; Faroni, C.C. Loosening of Fasteners by Vibration; Report No. ER272-2177; Elastic Stop Nut Corp. Am. (ESNA): Union, NJ, USA, 1966.
Zhang, M.; Jiang, Y.; Lee, C.-H. An Experimental Investigation of the Effects of Clamped Length and Loading Direction on Self-Loosening of Bolted Joints. J. Press. Vessel. Technol. Trans. ASME 2005, 128, 388–393.
Miller, M.; Johnson, C.; Sonne, N.; Mersch, J.; Kuether, R.J.; Smith, J.; Ortiz, J.; Castelluccio, G.; Moore, K. Bolt Preload Loss Due to Modal Excitation of a C-Beam Structure. In Nonlinear Structures & Systems; Springer: New York, NY, USA, 2020; pp. 203–214.
Eraliev, O.M.U.; Zhang, Y.-H.; Lee, K.-H.; Lee, C.-H. Experimental investigation on self-loosening of a bolted joint under cyclical temperature changes. Adv. Mech. Eng. 2021, 13, 1–8.

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.

Upload a video for this entry

Information

Subjects: Engineering, Mechanical

Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :

Dario Croccolo

Massimiliano De Agostinis

Stefano Fini

Mattia Mele

Giorgio Olmi

Chiara Scapecchi

Muhammad Hassaan Bin Tariq

View Times: 743

Update Date: 14 Feb 2023

Table of Contents

Video Upload Options

Confirm