Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Majid Siavashi
 -- 2063 2023-02-11 22:16:14 |
2 layout
Sirius Huang
 Meta information modification 2063 2023-02-13 02:08:37 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Shirbani, M.;  Siavashi, M.;  Bidabadi, M. Improvement of Energy Storage in Phase Change Materials. Encyclopedia. Available online: https://encyclopedia.pub/entry/41123 (accessed on 27 July 2024).
Shirbani M,  Siavashi M,  Bidabadi M. Improvement of Energy Storage in Phase Change Materials. Encyclopedia. Available at: https://encyclopedia.pub/entry/41123. Accessed July 27, 2024.
Shirbani, Milad, Majid Siavashi, Mehdi Bidabadi. "Improvement of Energy Storage in Phase Change Materials" Encyclopedia, https://encyclopedia.pub/entry/41123 (accessed July 27, 2024).
Shirbani, M.,  Siavashi, M., & Bidabadi, M. (2023, February 11). Improvement of Energy Storage in Phase Change Materials. In Encyclopedia. https://encyclopedia.pub/entry/41123
Shirbani, Milad, et al. "Improvement of Energy Storage in Phase Change Materials." Encyclopedia. Web. 11 February, 2023.
Improvement of Energy Storage in Phase Change Materials
Edit
This entry is adapted from the peer-reviewed paper 10.3390/en16031059

Utilizing phase change materials (PCMs) is one of the most effective methods of storing thermal energy and is gaining popularity in renewable energy systems. In order to analyze PCM performance, various numerical methods have been deployed to study the transient behaviour during phase changes. PCMs’ low thermal conductivity prevents their use as pure PCMs in industrial applications. There are various efficient methods of enhancing PCM thermal conductivity.

thermal energy storage performance enhancement lattice Boltzmann method (LBM) porous media nanoparticle phase change material (PCM)

1. Introduction

Thermal energy could be stored in two different ways: sensible and latent. Energy storage using sensible heat uses a solid or liquid medium without a phase change as an energy carrier, while latent heat energy storage (LHTES) uses the phase change enthalpy during melting or solidification to store energy. LHTES provides higher heat storage capacity with a lower weight and volume of the material than the sensible type. Using phase change materials (PCMs) for storing latent heat is the top-rated on the list of developed, applied, and investigated energy storage methods [1][2]. In PCMs, supplying or extracting energy is performed via a slight temperature change during the phase change, and the phase change occurs in an intermediate temperature range [3]. Another application of PCMs is thermal management and temperature control [4], for example, the thermal protection of electronic devices against pulsed power loads [5] or battery temperature management [6]. The worst thing about PCMs blocking their way to becoming a reliable method of energy storage is their low thermal conductivity. 
PCM performance improvement may be briefed as the thermal conductivity enhancement of the PCM material. Therefore, many studies have been established to find methods to reach more significant thermal conductivities of PCMs. These studies also have led to collateral effects, such as lower volume changes during the phase change, more uniform temperature distributions, shorter charging times, and more. Here, some effective methods for PCM improvements are summarized.

2. Porous Media as Composite PCMs

A reliable scheme to improve PCM thermal conductivity is using highly porous structures as catalysts with high thermal conductivities. In general, implementing porous media and composite PCMs could be two different methods of PCM enhancement. However, all known composite PCMs are usually porous media. Therefore, here, these two methods are combined and defined as one single coupled method.
Since this text concentrates on lattice Boltzmann method applications in PCM studies, there are investigations in the simulation of porous media-filled cavities of PCMs. Wu et al. [7] studied the solid-liquid phase change problem considering convection heat transfer in porous media. Deploying a generalized model of the LB based on the Darcy-Brinkman-Forchheimer model considers the existence of the porous medium. The aim of the study and other correlated studies [8][9] was to illustrate the agreement between this model and previous analytical and numerical models. Another type of study in this scope has focused on the geometrical characteristics of the porous medium used to enhance the energy storage of PCMs. A recent study on this topic was from Mabrouk et al. [10], which investigated the porosity effects on this realm.

2.1. Metal Foam Composite PCMs

A key process in the provision of composite PCMs is impregnating PCMs into porous metals [4]. High thermal conductivity and the specific surface ratios of metal foams are the main reasons why they have attracted attention [11]. Metal foams significantly affect the phase change heat transfer of melting and solidification [12]. They shorten the charging time and construct a more uniform temperature distribution [13][14][15][16]. Adding metal substances to PCMs would lead to greater thermal conductivity [17]. Most of the disquisitions in this area have focused on foam geometry. Some has followed the LBM method, e.g., Gaedtke et al. [18] and Mabrouk et al. [10]. Others such as Sai Dinesh et al. [19][20] and Parida et al. [21] who investigated the porosity and pore size of metal foams implemented other schemes that simulate the flow through metal foams. They concluded that even for the same porosity value, a smaller pore size results in faster melting and a higher heat transfer rate. Furthermore, for lower porosities, the melting time is reduced due to the higher thermal conductivity (see Figure 1).
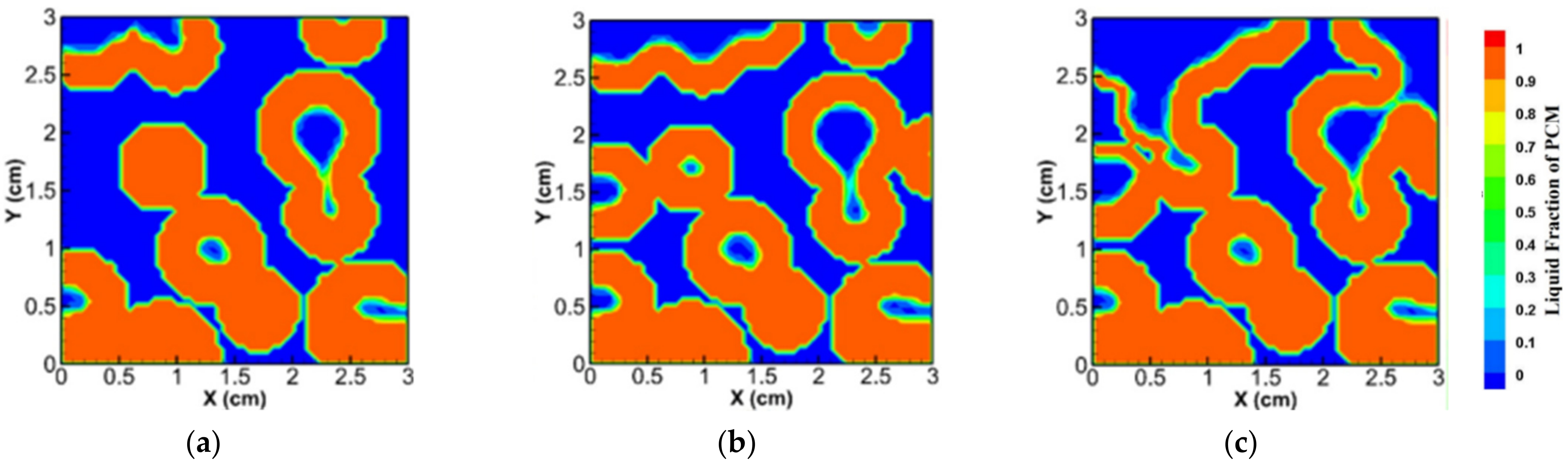
Figure 1. The melting front for different porosities of metal foams after 163 s performed by Parida et al. [21]; (a) 50% porosity, (b) 60% porosity, and (c) 70% porosity.
In a work conducted by Hu et al. [22], the pore density was explained. Low porosity and high pore density composite PCMs melt faster than high porosity and low pore density ones. As this method has the most visible impact on the melting process of PCMs, there are various experimental investigations in this area. For instance, Mohamed Moussa and Karkri [23] conducted a study on the effects of different heat condition types in metal foam-enhanced PCMs. The thermal behavior of a PCM filled with a low porosity metal foam was the target of an experimental study by Hu et al. [24], and more recently, the geometrical characteristics of a metal foam were investigated in a set of experiments which were led by Iasiello et al. [25]. A major concern of the studies in this area is whether the solution domain is three or two-dimensional. In three-dimensional domains, one could thoroughly study the effect of metal foam geometry as it has various conduction paths from behind and in front of the 2D section. However, in 2D studies, these conduction paths would not be declared. This phenomenon that would distinguish the conduction paths is critical in some applications to be observed, such as photovoltaic panels’ energy storage enhancement by adding metal foam-embedded PCMs, which was the main concern of a recent study by Li et al. [26]. Some problems addressed were energy storage tanks enhanced by PCMs impregnated with metal foams [27]. Despite the latter applications, which require 3D simulation studies, there are multiple applications that implement metal matrixes (not necessarily foams) that do not have complex geometries (such as open-cell irregular foams) and could be simplified in 2D studies without significantly affecting the results. Shirbani et al. [28] addressed these applications and implemented the LBM to study the effects of the geometrical characteristics of a solid matrix on the melting process of a PCM. Their main goal was to reach the best pore arrangement in cylindrical-shaped pores in a solid matrix along with the best pore diameter to reach the most enhanced performance of a PCM during melting. They concluded that a bigger mean pore diameter would help the natural convection, and then the arrangement would not affect the melting time. However, for a small pore mean diameter, the arrangement and conduction path thickness would be important.

2.2. Composite PCMs with Carbon Materials

Carbon nanomaterials, expanded graphite (EG), and graphene-based materials are examples of carbon materials that have been extensively studied and used as thermal conductivity-enhancing materials [4]. Carbon substances are suitable to formulate a solution with barely corrosive PCMs, such as salt hydrates. The fabrication processes of carbon/graphite foam composite PCMs [29][30][31][32] and graphene aerogel [33] are the same as metal foams, called the vacuum impregnation process. More applicable studies have been conducted recently, such as Polytetrafluoroethylene (PTFE)-based PCMs [34] and gypsum-based PCMs [35], which both use carbon fibers as the enhancement agent for the PCM.

3. Nanoparticle-Enhanced PCMs

A typical disadvantage of PCMs is their low thermal conductivity. Khodadadi et al. [36][37] were among the first researchers who came up with the idea of dispersing high thermal conductivity nanoparticles into PCMs. According to the results of their study, the application diversity of PCMs could be increased when the thermal conductivity of the PCM is improved.
Recent studies were conducted to report LBM implementation on the simulation of nanoparticle-enhanced phase change material (NEPCM) heat transfer. Jourabian et al. [38] studied the LBM application in simulating ice melting enhanced with Cu nanoparticles. They presented a good concurrence between their numerical results and those of previous numerical and experimental methods. They also declared that adding nanoparticles would hasten the melting process. Then, Feng et al. [39] conducted a study on the same material with a novel LB method and different boundary conditions. Their results approved the previously mentioned work, and they concluded that by increasing the nanoparticles’ volume fraction, the stored energy and molten fraction would increase, in line with faster development in the temperature field and melting interface.
Ibrahem et al. [40], in their work, could add one more characteristic change in PCMs when improved by adding nanoparticles. They explained that the presence of nanoparticles enhanced the movement of the phase change front, summarized in Figure 2. Ren et al. [41] studied the melting process of nanoparticle and metal foam-enhanced PCMs in a heat pipe. They concluded that increasing the porosity of metal foams or increasing the nanoparticle volume fraction would speed up the melting process of nanoparticle PCMs. Moreover, they mentioned that the immersed boundary enthalpy-based lattice Boltzmann method would be a suitable method for a numerical study on this matter. Recent studies addressed the complex geometries and combinations of various PCM enhancement methods. For instance, in the work published by Jourabian et al. [42], the geometry was an inclined elliptical annulus, and the NEPCM was combined with porous media and a metal matrix. They concluded that for inclined geometries, it is better to use the solid matrix in PCMs to have stable stratification. Recently Peng and Sadaghiani [43] studied the effect of alumina nanoparticle-enhanced PCMs around a cylindrical battery in a rectangular finned domain. Adding a slope to the geometry of the later problem, meaning the study of an inclined finned domain consisting of hybrid nanoparticle-enhanced PCMs, is what Laouer et al. [44] studied. They reported the effect of the number of fins and their optimum length ratios. Adding fins to a domain-containing PCM is another way of increasing the heat transfer coefficient and is reviewed in the next section.
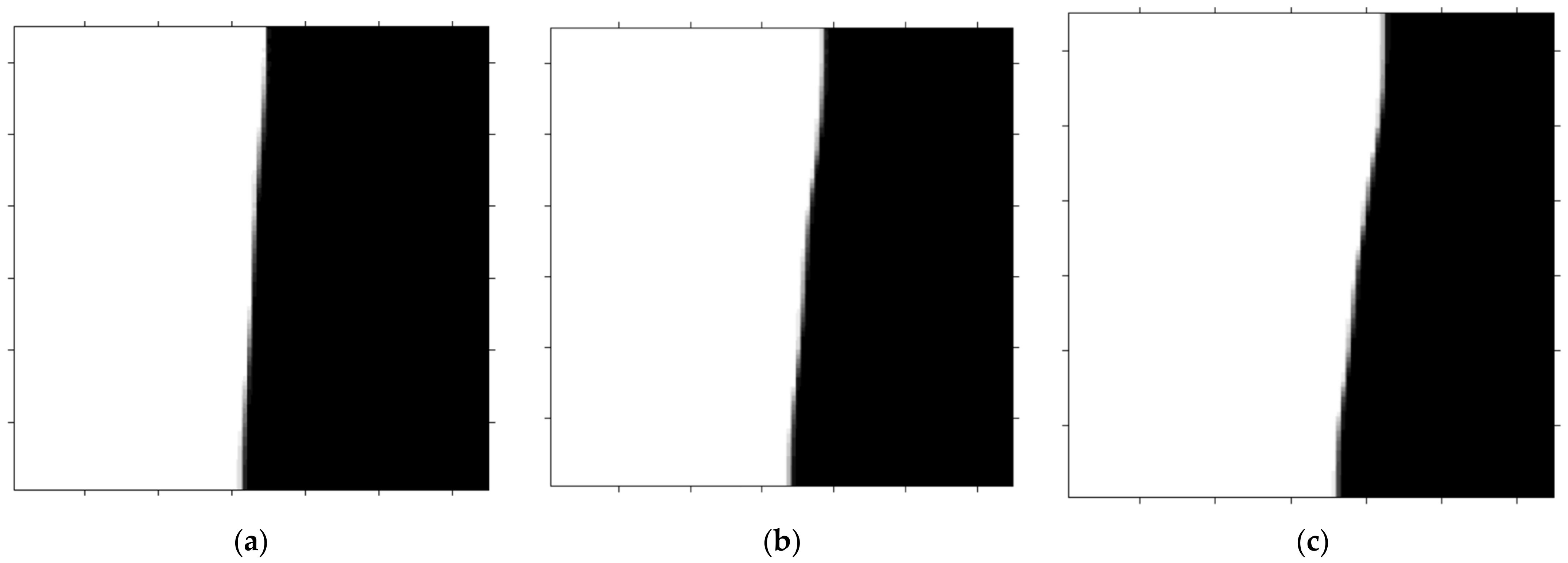
Figure 2. Interface positions in the Ibrahem et al. [40] study. (a) Pure water, (b) nano-PCM No.1, and (c) nano-PCM No.2.

4. Effect of Adding Fins

A common, straightforward, and applicable way to improve the thermal conductivity of PCMs is through the use of extended surfaces called fins. However, this has some drawbacks, such as increased system weight [4]. Here, the main goal is to review LBM-based studies on the effects of fins on the phase change behavior of PCMs.
Talati and Taghilou [45][46] investigated the LBM application on solidification in a finned container. In their study, they defined the optimum aspect ratio of the container to maximize the solidification time, which was 0.5. Also, they concluded that changing the fin’s material would not significantly impact the results. As a complementary study to their previous work, they conducted a study on the melting of a PCM in the same conditions [47]. As an additional result, they found that moving a solid body would accelerate the melting process.
As a novel study, Ren and Chan [48] implemented a multi-relaxation time (MRT)-LBM to simulate the heat transfer of finned PCMs. Their first major result was the development of the method that they implemented. The secondary results illustrated that by increasing the number of fins, the melting process was completed faster (see Figure 3). Furthermore, the melting rate grew when the length of the inner fins expanded, despite a limit. They found, however, that fewer long fins were more effective than more short fins.
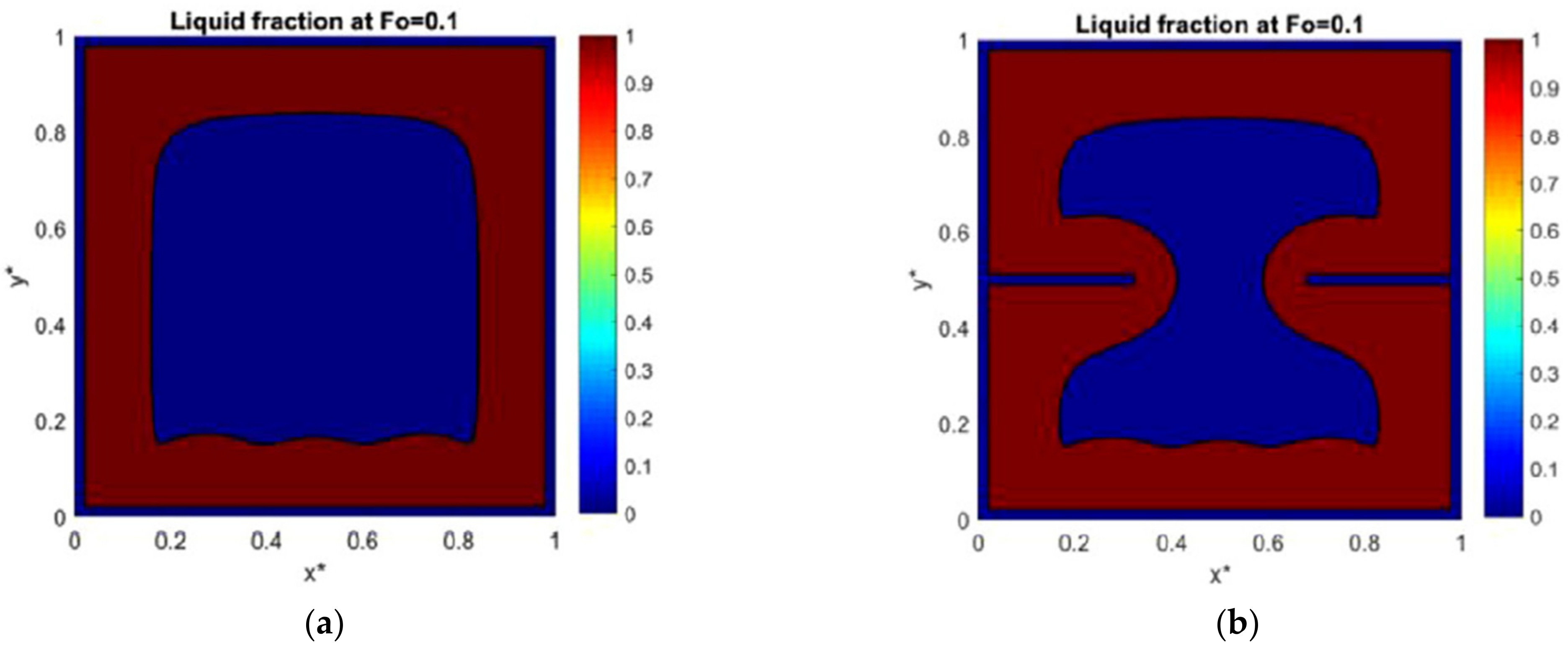
Figure 3. Comparison of melting fronts for a cavity (a) without fins and (b) with fins from the study published by Ren and Chan [48].
A phase change material coupled with conduction fins was also simulated using the MRT-LBM for transient melting heat transferrin, a work published by Gao et al. [47]. Their novelty was the coupling of the MRT-LBM with the representative element volume scale (REV-scale). Their results indicated the same conclusion as that of Ren and Chan [48], as previously addressed. Recent studies corresponding to adding fins in geometries to enhance the energy storage of PCMs are also about a combination of the enhancement methods, such as the NEPCM. Regardless of the simulation method, Chu et al. [49] incorporated the NEPCMs by using a finned tank to enhance the energy storage of PCMs. The focus of their work was energy loss in various cases of the layouts of fins. As a recent study of the combined enhancement methods of PCMs, Yang et al. [50] decided to investigate the effect of adding a metal foam to a finned shell and tube consisting of a PCM and concluded that this action decreased the nonuniformity of solidification and temperature distribution; the authors also mentioned that this hybrid method would lead to a 90.5% reduction in the total energy released compared to a pure PCM unit.

References

  1. Twaha, S.; Zhu, J.; Yan, Y.; Li, B. A comprehensive review of thermoelectric technology: Materials, applications, modelling and performance improvement. Renew. Sustain. Energy Rev. 2016, 65, 698–726.
  2. Da Cunha, J.P.; Eames, P. Thermal energy storage for low and medium temperature applications using phase change materials—A review. Appl. Energy 2016, 177, 227–238.
  3. Matuszek, K.; Kar, M.; Pringle, J.M.; MacFarlane, D.R. Phase Change Materials for Renewable Energy Storage at Intermediate Temperatures. Chem. Rev. 2022, 123, 491–514.
  4. Zhang, P.; Xiao, X.; Ma, Z.W. A review of the composite phase change materials: Fabrication, characterization, mathematical modeling and application to performance enhancement. Appl. Energy 2016, 165, 472–510.
  5. Shaikh, S.; Lafdi, K. C/C composite, carbon nanotube and paraffin wax hybrid systems for the thermal control of pulsed power in electronics. Carbon 2010, 48, 813–824.
  6. Luo, J.; Zou, D.; Wang, Y.; Wang, S.; Huang, L. Battery thermal management systems (BTMs) based on phase change material (PCM): A comprehensive review. Chem. Eng. J. 2021, 430, 132741.
  7. Wu, W.; Zhang, S.; Wang, S. A novel lattice Boltzmann model for the solid–liquid phase change with the convec-tion heat transfer in the porous media. Int. J. Heat Mass Transf. 2017, 104, 675–687.
  8. Jourabian, M.; Darzi, A.A.R.; Toghraie, D.; Akbari, O.A. Melting process in porous media around two hot cylinders: Numerical study using the lattice Boltzmann method. Phys. A Stat. Mech. Its Appl. 2018, 509, 316–335.
  9. Gao, D.; Chen, Z. Lattice Boltzmann simulation of natural convection dominated melting in a rectangular cavity filled with porous media. Int. J. Therm. Sci. 2011, 50, 493–501.
  10. Mabrouk, R.; Naji, H.; Dhahri, H.; Hammouda, S.; Younsi, Z. Numerical investigation of porosity effect on a PCM’s thermal performance in a porous rectangular channel via thermal lattice Boltzmann method. Int. Commun. Heat Mass Transf. 2020, 119, 104992.
  11. Tao, Y.; You, Y.; He, Y. Lattice Boltzmann simulation on phase change heat transfer in metal foams/paraffin composite phase change material. Appl. Therm. Eng. 2016, 93, 476–485.
  12. Zhao, C.Y.; Lu, W.; Tian, Y. Heat transfer enhancement for thermal energy storage using metal foams embedded within phase change materials (PCMs). Sol. Energy 2010, 84, 1402–1412.
  13. Cui, H.T. Experimental investigation on the heat charging process by paraffin filled with high porosity cop-per foam. Appl. Therm. Eng. 2012, 39, 26–28.
  14. Mancin, S.; Diani, A.; Doretti, L.; Hooman, K.; Rossetto, L. Experimental analysis of phase change phenom-enon of paraffin waxes embedded in copper foams. Int. J. Therm. Sci. 2015, 90, 79–89.
  15. Wang, Z.; Zhang, Z.; Jia, L.; Yang, L. Paraffin and paraffin/aluminum foam composite phase change mate-rial heat storage experimental study based on thermal management of Li-ion battery. Appl. Therm. Eng. 2015, 78, 428–436.
  16. Sundarram, S.S.; Li, W. The effect of pore size and porosity on thermal management performance of phase change material infiltrated microcellular metal foams. Appl. Therm. Eng. 2014, 64, 147–154.
  17. Xiao, X.; Zhang, P.; Li, M. Effective thermal conductivity of open-cell metal foams impregnated with pure paraffin for latent heat storage. Int. J. Therm. Sci. 2014, 81, 94–105.
  18. Gaedtke, M.; Abishek, S.; Mead-Hunter, R.; King, A.J.C.; Mullins, B.J.; Nirschl, H.; Krause, M.J. Total enthalpy-based lattice Boltzmann simulations of melting in paraffin/metal foam composite phase change materials. Int. J. Heat Mass Transf. 2020, 155, 119870.
  19. Dinesh, B.V.S.; Bhattacharya, A. Effect of foam geometry on heat absorption characteristics of PCM-metal foam composite thermal energy storage systems. Int. J. Heat Mass Transf. 2019, 134, 866–883.
  20. Dinesh, B.V.S.; Bhattacharya, A. Comparison of energy absorption characteristics of PCM-metal foam systems with different pore size distributions. J. Energy Storage 2020, 28, 101190.
  21. Parida, A.; Bhattacharya, A.; Rath, P. Effect of convection on melting characteristics of phase change material-metal foam composite thermal energy storage system. J. Energy Storage 2020, 32, 101804.
  22. Hu, X.; Gong, X. Pore-scale numerical simulation of the thermal performance for phase change material embedded in metal foam with cubic periodic cell structure. Appl. Therm. Eng. 2019, 151, 231–239.
  23. Moussa, E.I.M.; Karkri, M. A numerical investigation of the effects of metal foam characteristics and heating/cooling conditions on the phase change kinetic of phase change materials embedded in metal foam. J. Energy Storage 2019, 26, 100985.
  24. Chen, Z.; Gao, D.; Shi, J. Experimental and numerical study on melting of phase change materials in metal foams at pore scale. Int. J. Heat Mass Transf. 2014, 72, 646–655.
  25. Iasiello, M.; Mameli, M.; Filippeschi, S.; Bianco, N. Metal foam/PCM melting evolution analysis: Orientation and morphology effects. Appl. Therm. Eng. 2021, 187, 116572.
  26. Li, X.; Duan, J.; Simon, T.; Ma, T.; Cui, T.; Wang, Q. Nonuniform metal foam design and pore-scale analysis of a tilted composite phase change material system for photovoltaics thermal management. Appl. Energy 2021, 298, 117203.
  27. Liu, G.; Xiao, T.; Guo, J.; Wei, P.; Yang, X.; Hooman, K. Melting and solidification of phase change materials in metal foam filled thermal energy storage tank: Evaluation on gradient in pore structure. Appl. Therm. Eng. 2022, 212, 118564.
  28. Shirbani, M.; Siavashi, M.; Hosseini, M.; Bidabadi, M. Improved thermal energy storage with metal foam enhanced phase change materials considering various pore arrangements: A pore-scale parallel lattice Boltzmann solution. J. Energy Storage 2022, 52, 104744.
  29. Zhong, Y.; Guo, Q.; Li, S.; Shi, J.; Liu, L. Heat transfer enhancement of paraffin wax using graphite foam for thermal energy storage. Sol. Energy Mater. Sol. Cells 2010, 94, 1011–1014.
  30. Zhong, Y.; Guo, Q.; Li, S.; Shi, J.; Liu, L. Thermal and mechanical properties of graphite foam/Wood’s alloy composite for thermal energy storage. Carbon 2010, 48, 1689–1692.
  31. Zhong, Y.; Guo, Q.; Li, L.; Wang, X.; Song, J.; Xiao, K.; Huang, F. Heat transfer improvement of Wood’s alloy using compressed expanded natural graphite for thermal energy storage. Sol. Energy Mater. Sol. Cells 2012, 100, 263–267.
  32. Xiao, X.; Zhang, P. Morphologies and thermal characterization of paraffin/carbon foam composite phase change material. Sol. Energy Mater. Sol. Cells 2013, 117, 451–461.
  33. Zhong, Y.; Zhou, M.; Huang, F.; Lin, T.; Wan, D. Effect of graphene aerogel on thermal behavior of phase change materials for thermal management. Sol. Energy Mater. Sol. Cells 2013, 113, 195–200.
  34. Markova, M.A.; Petrova, P.N. Influence of Carbon Fibers and Composite Technologies on the Properties of PCM Based on Polytetrafluoroethylene. Inorg. Mater. Appl. Res. 2021, 12, 551–557.
  35. Zhang, B.; Yang, H.; Xu, T.; Tang, W.; Cui, H. Mechanical and Thermo-Physical Performances of Gypsum-Based PCM Composite Materials Reinforced with Carbon Fi-ber. Appl. Sci. 2021, 11, 468.
  36. Khodadadi, J.; Fan, L.; Babaei, H. Thermal conductivity enhancement of nanostructure-based colloidal suspensions utilized as phase change materials for thermal energy storage: A review. Renew. Sustain. Energy Rev. 2013, 24, 418–444.
  37. Khodadadi, J.; Hosseinizadeh, S. Nanoparticle-enhanced phase change materials (NEPCM) with great potential for improved thermal energy storage. Int. Commun. Heat Mass Transf. 2007, 34, 534–543.
  38. Jourabian, M.; Farhadi, M.; Darzi, A.A.R. Outward melting of ice enhanced by Cu nanoparticles inside cylindrical horizontal annulus: Lattice Boltzmann approach. Appl. Math. Model. 2013, 37, 8813–8825.
  39. Feng, Y.; Li, H.; Li, L.; Bu, L.; Wang, T. Numerical investigation on the melting of nanoparticle-enhanced phase change materials (NEPCM) in a bottom-heated rectangular cavity using lattice Boltzmann method. Int. J. Heat Mass Transf. 2015, 81, 415–425.
  40. Ibrahem, A.M.; El-Amin, M.F.; Sun, S. Effects of nanoparticles on melting process with phase-change using the lattice Boltzmann method. Results Phys. 2017, 7, 1676–1682.
  41. Ren, Q.; Meng, F.; Guo, P. A comparative study of PCM melting process in a heat pipe-assisted LHTES unit enhanced with nanoparticles and metal foams by immersed boundary-lattice Boltzmann method at pore-scale. Int. J. Heat Mass Transf. 2018, 121, 1214–1228.
  42. Jourabian, M.; Darzi, A.A.R.; Akbari, O.A.; Toghraie, D. The enthalpy-based lattice Boltzmann method (LBM) for simulation of NePCM melting in inclined elliptical annulus. Phys. A Stat. Mech. Its Appl. 2019, 548, 123887.
  43. Peng, W.; Sadaghiani, O.K. Thermal function improvement of phase-change material (PCM) using alumina nanoparticles in a circular-rectangular cavity using Lattice Boltzmann method. J. Energy Storage 2021, 37, 102493.
  44. Laouer, A.; Teggar, M.; Tunçbilek, E.; Arıcı, M.; Hachani, L.; Ismail, K.A. Melting of hybrid nano-enhanced phase change material in an inclined finned rectangular cavity for cold energy storage. J. Energy Storage 2022, 50, 104185.
  45. Talati, F.; Taghilou, M. Lattice Boltzmann application on the PCM solidification within a rectangular finned container. Appl. Therm. Eng. 2015, 83, 108–120.
  46. Taghilou, M.; Talati, F. Numerical investigation on the natural convection effects in the melting process of PCM in a finned container using lattice Boltzmann method. Int. J. Refrig. 2016, 70, 157–170.
  47. Gao, D.; Chen, Z.; Zhang, D.; Chen, L. Lattice Boltzmann modeling of melting of phase change materials in porous media with conducting fins. Appl. Therm. Eng. 2017, 118, 315–327.
  48. Ren, Q.; Chan, C.L. GPU accelerated numerical study of PCM melting process in an enclosure with internal fins using lattice Boltzmann method. Int. J. Heat Mass Transf. 2016, 100, 522–535.
  49. Chu, Y.-M.; Abu-Hamdeh, N.H.; Ben-Beya, B.; Hajizadeh, M.R.; Li, Z.; Bach, Q.-V. Nanoparticle enhanced PCM exergy loss and thermal behavior by means of FVM. J. Mol. Liq. 2020, 320, 114457.
  50. Yang, X.; Xu, F.; Wang, X.; Guo, J.; Li, M.-J. Solidification in a shell-and-tube thermal energy storage unit filled with longitude fins and metal foam: A numerical study. Energy Built Environ. 2021, 4, 64–73.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Engineering, Mechanical; Materials Science, Composites
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Milad Shirbani
,
Majid Siavashi
,
Mehdi Bidabadi
View Times: 587
Revisions: 2 times (View History)
Update Date: 13 Feb 2023
Table of Contents
    1000/1000
    Hot Most Recent
    Video Production Service
    Feedback