Video Upload Options
Squeeze flow (also called squeezing flow, squeezing film flow, or squeeze flow theory) is a type of flow in which a material is pressed out or deformed between two parallel plates or objects. First explored in 1874 by Josef Stefan, squeeze flow describes the outward movement of a droplet of material, its area of contact with the plate surfaces, and the effects of internal and external factors such as temperature, viscoelasticity, and heterogeneity of the material. Several squeeze flow models exist to describe Newtonian and non-Newtonian fluids undergoing squeeze flow under various geometries and conditions. Numerous applications across scientific and engineering disciplines including rheometry, welding engineering, and materials science provide examples of squeeze flow in practical use.
1. Basic Assumptions
Conservation of mass (expressed as a continuity equation), the Navier-Stokes equations for conservation of momentum, and the Reynolds number provide the foundations for calculating and modeling squeeze flow. Boundary conditions for such calculations include assumptions of an incompressible fluid, a two-dimensional system, neglecting of body forces, and neglecting of inertial forces.
Relating applied force to material thickness:
[math]\displaystyle{ F=-\frac{4*L^3*\eta*W}{h^3}{dh \over dt} }[/math]
Where [math]\displaystyle{ F }[/math] is the applied squeezing force, [math]\displaystyle{ 2L }[/math] is the initial length of the droplet, [math]\displaystyle{ \eta }[/math] is the fluid viscosity, [math]\displaystyle{ W }[/math] is the width of the assumed rectangular plate, [math]\displaystyle{ 2h }[/math] is the final height of the droplet, and [math]\displaystyle{ {dh \over dt} }[/math]is the change in droplet height over time. To simplify most calculations, the applied force is assumed to be constant.

1.1. Newtonian Fluids
Several equations accurately model Newtonian droplet sizes under different initial conditions.
Consideration of a single asperity, or surface protrusion, allows for measurement of a very specific cross-section of a droplet. To measure macroscopic squeeze flow effects, models exist for two the most common surfaces: circular and rectangular plate squeeze flows.
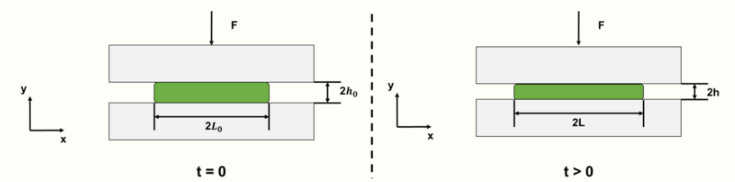
Single asperity
For single asperity squeeze flow:
[math]\displaystyle{ \frac{h_0}{h}=\left (1+\frac{5*F*t*h_0^2}{4*\eta*W*L_0^3}\right )^{1/5} }[/math]
Where [math]\displaystyle{ 2h_0 }[/math] is the initial height of the droplet, [math]\displaystyle{ 2h }[/math] is the final height of the droplet, [math]\displaystyle{ F }[/math] is the applied squeezing force, [math]\displaystyle{ t }[/math] is the squeezing time, [math]\displaystyle{ \eta }[/math] is the fluid viscosity, [math]\displaystyle{ W }[/math] is the width of the assumed rectangular plate, and [math]\displaystyle{ 2L_0 }[/math] is the initial length of the droplet.[1]
Based on conservation of mass calculations, the droplet width is inversely proportional to droplet height; as the width increases, the height decreases in response to squeezing forces.[1]
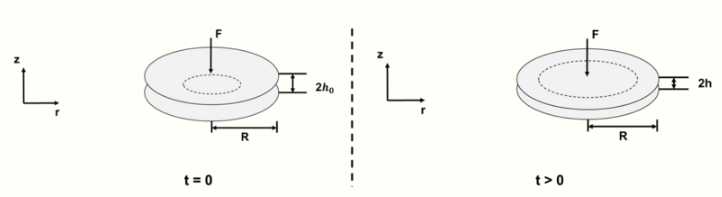
Circular plate squeeze flow diagram at initial and follow-on conditions; circular plates (gray), droplet (hash marked ellipse between both plates). https://handwiki.org/wiki/index.php?curid=1881082
Circular plate
For circular plate squeeze flow:
[math]\displaystyle{ \frac{h_0}{h}=\left (1+\frac{16*F*t*h_0^2}{3*\pi*\eta*R^4}\right )^{1/2} }[/math]
[math]\displaystyle{ R }[/math] is the radius of the circular plate.[1]
Rectangular plate
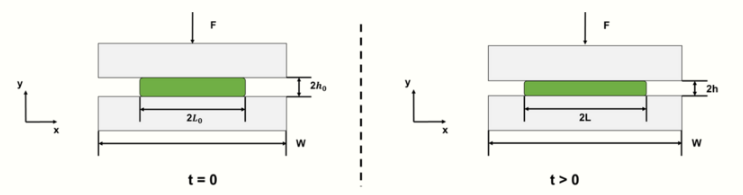
For rectangular plate squeeze flow:
[math]\displaystyle{ \frac{h_0}{h}=\left (1+\frac{F*t*h_0^2}{2*\mu*W*L^3}\right )^{1/2} }[/math]
These calculations assume a melt layer that has a length much larger than the sample width and thickness.[1]
1.2. Non-Newtonian Fluids
Simplifying calculations for Newtonian fluids allows for basic analysis of squeeze flow, but many polymers can exhibit properties of non-Newtonian fluids, such as viscoelastic characteristics, under deformation. The power law fluid model is sufficient to describe behaviors above the melting temperature for semicrystalline thermoplastics or the glass transition temperature for amorphous thermoplastics, and the Bingham fluid model provides calculations based on variations in yield stress calculations.[1][2]
Power law fluid
For squeeze flow in a power law fluid:
[math]\displaystyle{ \frac{h_0}{h}=\left ( 1+t*(\frac{2n+3}{4n+2})(\frac{(4*h_0*L_0)^{n+1}*F*(n+2)}{(2*L_0)^{2n+3}*W*m})^{1/n}\right )^{n/2n+3} }[/math]
Where [math]\displaystyle{ m }[/math] (or [math]\displaystyle{ K }[/math]) is the flow consistency index and [math]\displaystyle{ n }[/math] is the dimensionless flow behavior index.[1]
[math]\displaystyle{ m=m_0*exp\left ( \frac{-E_a}{R*T} \right ) }[/math]
Where [math]\displaystyle{ m }[/math] is the flow consistency index, [math]\displaystyle{ m_0 }[/math]is the initial flow consistency index, [math]\displaystyle{ E_a }[/math]is the activation energy, [math]\displaystyle{ R }[/math]is the universal gas constant, and [math]\displaystyle{ T }[/math]is the absolute temperature.[1]
During experimentation to determine the accuracy of the power law fluid model, observations showed that modeling slow squeeze flow generated inaccurate power law constants ([math]\displaystyle{ m }[/math]and [math]\displaystyle{ n }[/math]) using a standard viscometer, and fast squeeze flow demonstrated that polymers may exhibit better lubrication than current constitutive models will predict.[3] The current empirical model for power law fluids is relatively accurate for modeling inelastic flows, but certain kinematic flow assumptions and incomplete understanding of polymeric lubrication properties tend to provide inaccurate modeling of power law fluids.[3]
Bingham fluid
Bingham fluids exhibit uncommon characteristics during squeeze flow. While undergoing compression, Bingham fluids should fail to move and act as a solid until achieving a yield stress; however, as the parallel plates move closer together, the fluid shows some radial movement. One study proposes a “biviscosity” model where the Bingham fluid retains some unyielded regions that maintain solid-like properties, while other regions yield and allow for some compression and outward movement.[2]
[math]\displaystyle{ \tau = \begin{cases} \eta_2*{du \over dy}+\tau_1, & \text{if }\tau\geq\tau_1 \\ \eta_1*{du \over dy}, & \text{if }\tau\lt \tau_1 \end{cases} }[/math]
Where [math]\displaystyle{ \eta_2 }[/math] is the known viscosity of the Bingham fluid, [math]\displaystyle{ \eta_1 }[/math] is the "paradoxical" viscosity of the solid-like state, and [math]\displaystyle{ \tau_1 }[/math] is the biviscosity region stress.[2] To determine this new stress:
[math]\displaystyle{ \tau_0=\tau_1(1-\epsilon) }[/math]
Where [math]\displaystyle{ \tau_0 }[/math] is the yield stress and [math]\displaystyle{ \epsilon=\frac{\eta_2}{\eta_1} }[/math] is the dimensionless viscosity ratio. If [math]\displaystyle{ \epsilon=1 }[/math], the fluid exhibits Newtonian behavior; as [math]\displaystyle{ \epsilon\rightarrow0 }[/math], the Bingham model applies.[2]
2. Applications
Squeeze flow application is prevalent in several science and engineering fields. Modeling and experimentation assist with understanding the complexities of squeeze flow during processes such as rheological testing, hot plate welding, and composite material joining.
2.1. Rheological Testing
Squeeze flow rheometry allows for evaluation of polymers under wide ranges of temperatures, shear rates, and flow indexes. Parallel plate plastometers provide analysis for high viscosity materials such as rubber and glass, cure times for epoxy resins, and fiber-filled suspension flows.[4] While viscometers provide useful results for squeeze flow measurements, testing conditions such as applied rotation rates, material composition, and fluid flow behaviors under shear may require the use of rheometers or other novel setups to obtain accurate data.[3]
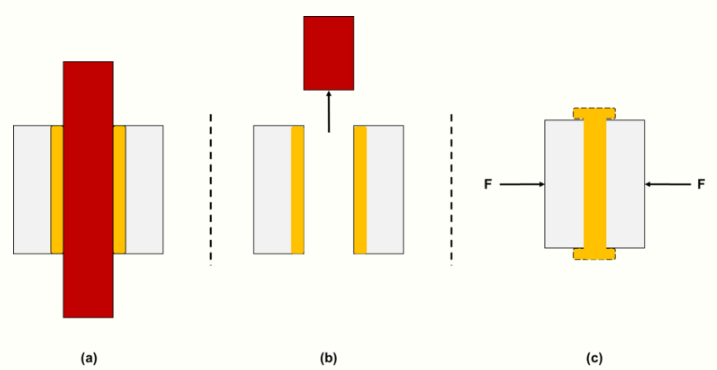
2.2. Hot Plate Welding
During conventional hot plate welding, a successful joining phase depends on proper maintenance of squeeze flow to ensure that pressure and temperature create an ideal weld. Excessive pressure causes squeeze out of valuable material and weakens the bond due to fiber realignment in the melt layer,[5] while failure to allow cooling to room temperature creates weak, brittle welds that crack or break completely during use.[1]
2.3. Composite Material Joining
Prevalent in the aerospace and automotive industries, composites serve as expensive, yet mechanically strong, materials in the construction of several types of aircraft and vehicles. While aircraft parts are typically composed of thermosetting polymers, thermoplastics may become an analog to permit increased manufacturing of these stronger materials through their melting abilities and relatively inexpensive raw materials. Characterization and testing of thermoplastic composites experiencing squeeze flow allow for study of fiber orientations within the melt and final products to determine weld strength.[5] Fiber strand length and size show significant effects on material strength,[6] and squeeze flow causes fibers to orient along the load direction while being perpendicular to the joining direction to achieve the same final properties as thermosetting composites.[5]
References
- Grewell, D., Benatar, A., & Park, J. (2013). Plastics and composites welding handbook. New York: Hanser.
- Wilson, S. (1993). Squeezing flow of a Bingham material. Journal of Non-Newtonian Fluid Mechanics, 47, 211-219. doi:10.1016/0377-0257(93)80051-c
- Grimm, Roger J. (1978). "Squeezing flows of polymeric liquids" (in en). AIChE Journal 24 (3): 427–439. doi:10.1002/aic.690240307. ISSN 1547-5905. https://dx.doi.org/10.1002%2Faic.690240307
- Macosko, C. W., & Larson, R. G. (1994). Rheology: Principles, measurements, and applications. New York: VCH.
- Fiebig, I., & Schoeppner, V. (2018). Factors influencing the fiber orientation in welding of fiber-reinforced thermoplastics. Welding in the World, 62(5), 997-1012. doi:10.1007/s40194-018-0628-0
- Picher-Martel, G., Levy, A., & Hubert, P. (2015). Compression molding of Carbon/Polyether ether ketone composites: Squeeze flow behavior of unidirectional and randomly oriented strands. Polymer Composites, 38(9), 1828-1837. doi:10.1002/pc.23753