
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Vivi Li | -- | 1246 | 2022-11-24 01:43:37 |
Video Upload Options
The Zisman plot the graphical method of the Zisman theory or the Zisman method for characterizing the wettability of a solid surface , named for the American chemist and geophysicist, William Albert Zisman (1905–1986). It is a prominent Sessile drop technique used for characterizing liquid-surface interactions based on the contact angle of a single drop of liquid sitting on the solid surface.
1. Zisman Plot
In 1964, William Zisman published an article in the ACS publications on the "Relation of the Equilibrium Contact Angle to Liquid and Solid Constitution".[1] It was in this article where he used what we call today as the Zisman plot. The Zisman plot is used to very quickly give a quantitative measurement of wettability, also known as the critical surface tension, γC , of a solid surface by measuring the liquid contact angle as shown in Figure 1. Taking the cosine of said angle and then graphing it against the surface tension of the liquid wetting the solid substrate yields the critical surface tension. Wettability is a measure of how well a liquid spreads and how complete the contact of the liquid is across the surface of a solid interface. A small contact angle indicates good wettability, while a large contact angle indicates poor wettability. The critical surface tension is the highest liquid surface tension that can completely wet a specific solid surface. For adhesive bonding complete wetting is used to maximize the adhesive joint strength.
-
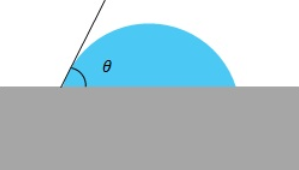
Figure 1: Schematic of a measured contact angle for a liquid on a solid substrate. Where θ is the contact angle denoted also in this case by θSL. https://handwiki.org/wiki/index.php?curid=1452643
Even though this relationship is empirical and less precise than the surface tension of a homologous series of liquids, it is very useful considering it is a parameter of the solid surface. This method is especially used to compare and measure the critical surface tension of low-energy solids (mainly plastics) very quickly and easily. Figure 4 in ZIsman's published article from 1964[1] shows the critical surface tension as a measure of wettability of Polyethylene. Zisman published this analysis in 1964 and used a variety of nonhomologous liquids to measure the critical surface tension of Polyethylene to be around 35 dynes per centimeter as shown by the intercept at x=1 in Figure 4. Figure 12 in Zisman's 1964 article[1] shows that different solids can also be plotted on the same graph to easily compare the critical solid surface tensions of a variety of plastic substrates including very different polymers such as teflon, acid monolayers, and esters. The ZIsman Plot proved to be a breakthrough which allowed for a very efficient way to measure wettability of a solid which helped to spawn the work of Dann in the late 1960s.[2] Dann characterized the critical surface tensions of a variety of polymeric materials using the Zisman Plot. In modern days, David and Neumann in an investigation of contact angle on low-energy surfaces.[3] However, today some different variations of the Zisman plot exist because the dependent variable is unitless being since it is cosine of the contact angle for the liquid.
2. Modern Day Zisman Plot Variation
For adhesive bonding of materials, wetting of the surface, which can be measured by the contact angle, is critical to successful adhesive application. To determine how well a liquid wets a solid surface is proportional to the contact angle from the liquid while on the solid. This is determined by the respective surface tensions of the solid and liquid. William Zisman's contribution to adhesives in the way of his Zisman Plot, which has a variation today that graphs 1-cos(θSL) vs γL . In this variation the X-intercept gives the critical surface tension of the liquid needed to effectively wet the solid surface. There are two steps when graphing the data which are to neglect all the points around zero on the y-axis to initially plot the line of best fit to find γc ; however, when graphing the line initially if a point near 0 lands to the right of the intersection redo the regression including that point to make the measurement of the critical surface tension, γc, more accurate. A table of variables and an example can be seen below.
3. Table of Variables
| Variable | Description | Units |
|---|---|---|
| θSL | The angle of a drop of the liquid on the solid as seen in Figure 1 | degrees or radians |
| 1-cos(θSL) | The y-axis of the Zisman Plot representing wetting | unitless |
| γL | The surface tension of the respective liquid | dyne / cm |
| γC | The critical surface tension of the liquid needed to effectively wet the solid substrate | dyne / cm |
4. Example
In this example we will use the five liquids in the Table 2 (Liquid Data) to find the critical wetting surface tension needed to effectively wet PC (polycarbonate) using the Zisman Plot.
| Liquid Number | (X-axis) Surface Tension (dyne/cm) | Contact Angle (degrees) | (Y-axis) 1-cos(θSL) |
|---|---|---|---|
| 1 | 27.7 | 10 | 0.0152 |
| 2 | 42.9 | 5 | 0.0038 |
| 3 | 57.2 | 43 | 0.2686 |
| 4 | 64.0 | 50 | 0.3572 |
| 5 | 72.8 | 60 | 0.5000 |
The data of the liquids given from the table above is then graphed on the Zisman Plot (Figure 2) with the independent variable as the surface tension of the liquid in dynes/cm and the dependent variable as 1-cos(θSL). There also are different variations of the Zisman plot since the Y-axis is unitless as seen in Table 1 and as mentioned above.
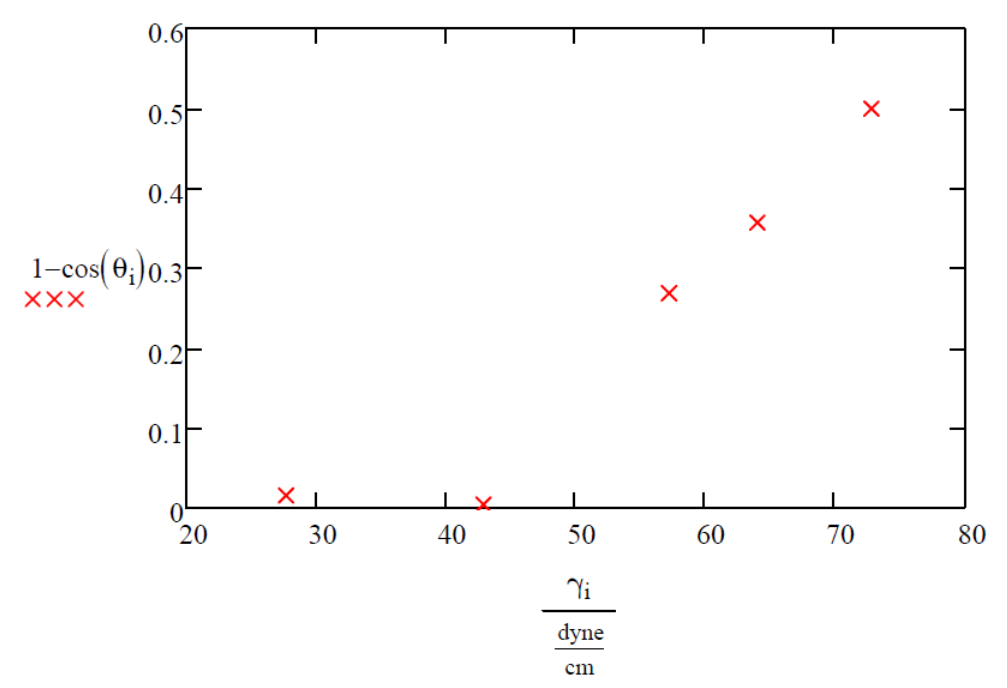
Liquids 1 and 2 fully wet the surface as shown by their low contact angles, so they should be neglected when first drawing the line of best fit to find the critical liquid surface tension needed to effectively wet the PC surface, γC, which is simply the x-intercept of the best fit line for the Zisman Plot. To find the best fit line a least squares regression is recommended by using a computer program such as Microsoft Excel, Minitab, Matlab, or it can also be done using a modern graphing calculator such as a TI-84. This was done with the data from Table 1 and the fit data for liquids 3,4, and 5 can be seen on Figure 3.
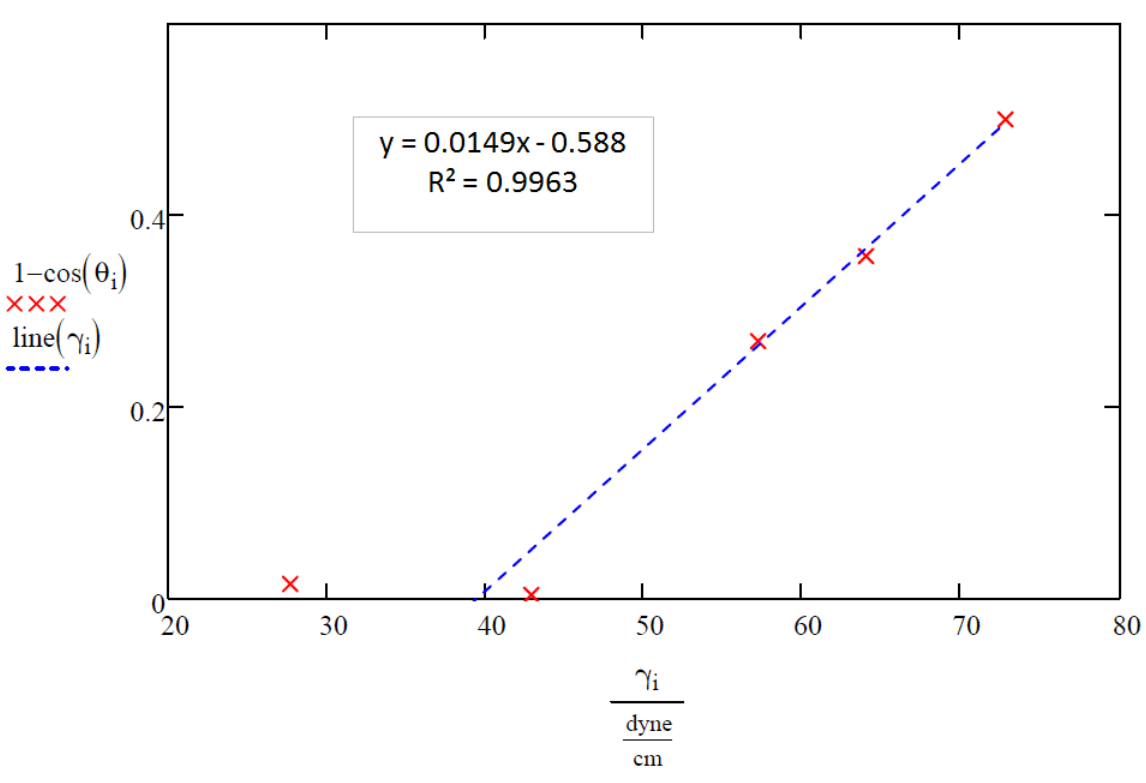
The x-intercept lands at 39.5 dynes per centimeter (This can be calculated by setting y equal to zero and solving for x) which is less than that of liquid 2, 42.9 dynes per centimeter; therefore, a more accurate measurement of the critical liquid surface tension needed to effectively wet the surface of PC can be obtained by including liquid 2 when making the line of best fit, as seen in Figure 4.
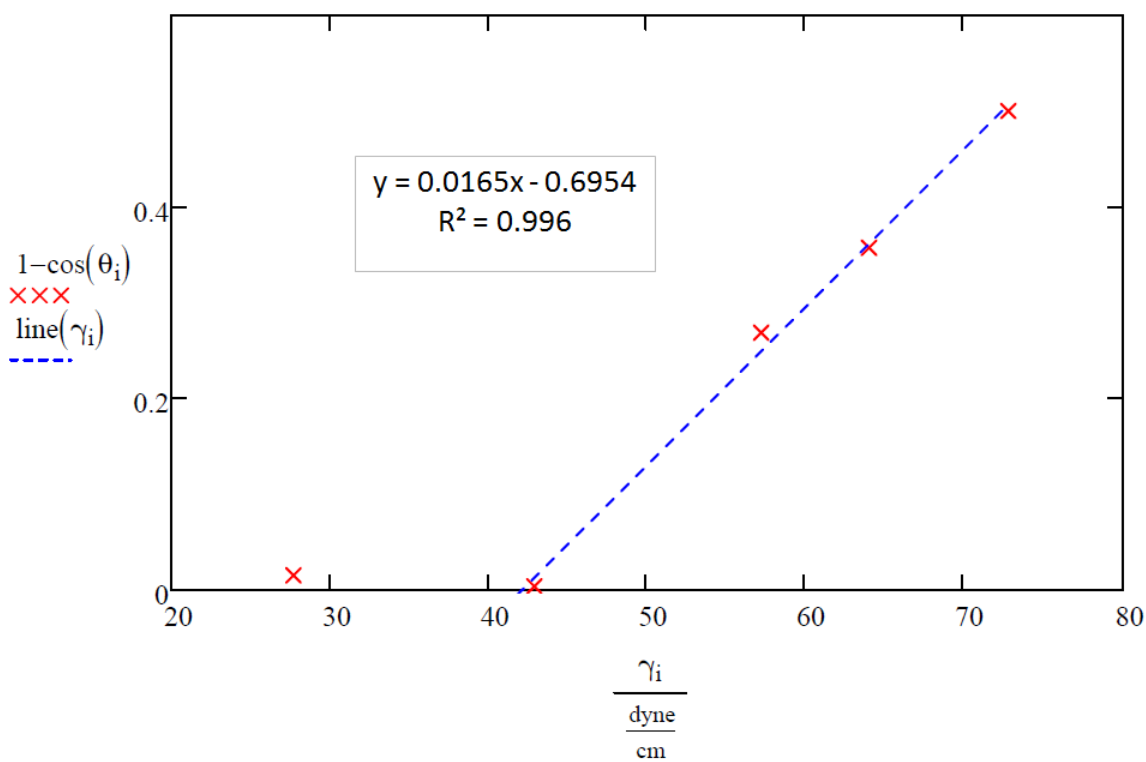
The x-intercept here lands at 42.1 dynes per centimeter (This can be calculated by setting y equal to zero and solving for x), indicating the critical liquid surface tension for PC.
5. Summary
William Zisman's contribution of what is called today as the Zisman Plot revolutionized the world of adhesive bonding and surface chemistry by giving a fast, effective, and quantitative way to measure the wettability or critical surface tension of a solid. This spawned the work of many others over the past few decades. This spans from Dann's work in the late 1960s to David and Neumann's work in 2014. The Zisman Plot is still used today, and it has many variations since the y-axis is unitless and can be found more easily and accurately using modern regression software packages.
References
- ZISMAN, W. A. (1964-01-01). Contact Angle, Wettability, and Adhesion. Advances in Chemistry. 43. AMERICAN CHEMICAL SOCIETY. pp. 1–51. doi:10.1021/ba-1964-0043.ch001. ISBN 0841200440. https://dx.doi.org/10.1021%2Fba-1964-0043.ch001
- Dann, J.R (1970). "Forces involved in the adhesive process". Journal of Colloid and Interface Science 32 (2): 302–320. doi:10.1016/0021-9797(70)90054-8. Bibcode: 1970JCIS...32..302D. https://dx.doi.org/10.1016%2F0021-9797%2870%2990054-8
- David, Robert; Neumann, A. Wilhelm (2014). "Contact Angle Patterns on Low-Energy Surfaces". Advances in Colloid and Interface Science 206: 46–56. doi:10.1016/j.cis.2013.03.005. https://dx.doi.org/10.1016%2Fj.cis.2013.03.005




