
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Beatrix Zheng | -- | 1473 | 2022-11-22 01:30:27 |
Video Upload Options
The Mie–Grüneisen equation of state is a relation between the pressure and the volume of a solid at a given temperature. It is used to determine the pressure in a shock-compressed solid. The Mie–Grüneisen relation is a special form of the Grüneisen model which describes the effect that changing the volume of a crystal lattice has on its vibrational properties. Several variations of the Mie–Grüneisen equation of state are in use. The Grüneisen model can be expressed in the form where V is the volume, p is the pressure, e is the internal energy, and Γ is the Grüneisen parameter which represents the thermal pressure from a set of vibrating atoms. If we assume that Γ is independent of p and e, we can integrate Grüneisen's model to get where p0 and e0 are the pressure and internal energy at a reference state usually assumed to be the state at which the temperature is 0K. In that case p0 and e0 are independent of temperature and the values of these quantities can be estimated from the Hugoniot equations. The Mie–Grüneisen equation of state is a special form of the above equation.
1. History
Gustav Mie, in 1903, developed an intermolecular potential for deriving high-temperature equations of state of solids.[1] In 1912 Eduard Grüneisen extended Mie's model to temperatures below the Debye temperature at which quantum effects become important.[2] Grüneisen's form of the equations is more convenient and has become the usual starting point for deriving Mie–Grüneisen equations of state.[3]
2. Expressions for the Mie–Grüneisen Equation of State
A temperature-corrected version that is used in computational mechanics has the form[4] (see also,[5] p. 61)
- [math]\displaystyle{ p = \frac{\rho_0 C_0^2 \chi \left[1 - \frac{\Gamma_0}{2}\,\chi\right]} {\left(1 - s\chi\right)^2} + \Gamma_0 E;\quad \chi := 1-\cfrac{\rho_0}{\rho} }[/math]
where [math]\displaystyle{ C_0 }[/math] is the bulk speed of sound, [math]\displaystyle{ \rho_0 }[/math] is the initial density, [math]\displaystyle{ \rho }[/math] is the current density, [math]\displaystyle{ \Gamma_0 }[/math] is Grüneisen's gamma at the reference state, [math]\displaystyle{ s = dU_s/dU_p }[/math] is a linear Hugoniot slope coefficient, [math]\displaystyle{ U_s }[/math] is the shock wave velocity, [math]\displaystyle{ U_p }[/math] is the particle velocity, and [math]\displaystyle{ E }[/math] is the internal energy per unit reference volume. An alternative form is
- [math]\displaystyle{ p = \frac{\rho_0 C_0^2 (\eta -1) \left[\eta - \frac{\Gamma_0}{2}(\eta-1)\right]} {\left[\eta - s(\eta-1)\right]^2} + \Gamma_0 E;\quad \eta := \cfrac{\rho}{\rho_0} \,. }[/math]
A rough estimate of the internal energy can be computed using
- [math]\displaystyle{ E = \frac{1}{V_0} \int C_v dT \approx \frac{C_v (T-T_0)}{V_0} = \rho_0 c_v (T-T_0) }[/math]
where [math]\displaystyle{ V_0 }[/math] is the reference volume at temperature [math]\displaystyle{ T = T_0 }[/math], [math]\displaystyle{ C_v }[/math] is the heat capacity and [math]\displaystyle{ c_v }[/math] is the specific heat capacity at constant volume. In many simulations, it is assumed that [math]\displaystyle{ C_p }[/math] and [math]\displaystyle{ C_v }[/math] are equal.
2.1. Parameters for Various Materials
| material | [math]\displaystyle{ \rho_0 }[/math] (kg/m3) | [math]\displaystyle{ c_v }[/math] (J/kg-K) | [math]\displaystyle{ C_0 }[/math] (m/s) | [math]\displaystyle{ s }[/math] | [math]\displaystyle{ \Gamma_0 }[/math] ([math]\displaystyle{ T \lt T_1 }[/math]) | [math]\displaystyle{ \Gamma_0 }[/math] ([math]\displaystyle{ T \gt = T_1 }[/math]) | [math]\displaystyle{ T_1 }[/math] (K) |
|---|---|---|---|---|---|---|---|
| Copper | 8960 | 390 | 3933 [6] | 1.5 [6] | 1.99 [7] | 2.12 [7] | 700 |
3. Derivation of the Equation of State
From Grüneisen's model we have
- [math]\displaystyle{ (1) \qquad p - p_0 = \frac{\Gamma}{V} (e - e_0) }[/math]
where p0 and e0 are the pressure and internal energy at a reference state. The Hugoniot equations for the conservation of mass, momentum, and energy are
- [math]\displaystyle{ \rho_0 U_s = \rho (U_s - U_p) ~~, \quad p_H - p_{H0} = \rho_0 U_s U_p \quad \text{and} \quad p_H U_p = \rho_0 U_s \left(\frac{U_p^2}{2} + E_H - E_{H0}\right) }[/math]
where ρ0 is the reference density, ρ is the density due to shock compression, pH is the pressure on the Hugoniot, EH is the internal energy per unit mass on the Hugoniot, Us is the shock velocity, and Up is the particle velocity. From the conservation of mass, we have
- [math]\displaystyle{ \frac{U_p}{U_s} = 1 - \frac{\rho_0}{\rho} = 1 - \frac{V}{V_0} =: \chi \,. }[/math]
Where we defined [math]\displaystyle{ V = 1/\rho }[/math], the specific volume (volume per unit mass).
- For many materials Us and Up are linearly related, i.e., Us = C0 + s Up where C0 and s depend on the material. In that case, we have
- [math]\displaystyle{ U_s = C_0 + s\chi U_s \quad \text{or} \quad U_s = \frac{C_0}{1 - s\chi} \,. }[/math]
The momentum equation can then be written (for the principal Hugoniot where pH0 is zero) as
- [math]\displaystyle{ p_H = \rho_0 \chi U_s^2 = \frac{\rho_0 C_0^2 \chi}{(1 - s\chi)^2} \,. }[/math]
Similarly, from the energy equation we have
- [math]\displaystyle{ p_H \chi U_s = \tfrac{1}{2} \rho \chi^2 U_s^3 + \rho_0 U_s E_H = \tfrac{1}{2} p_H \chi U_s + \rho_0 U_s E_H \,. }[/math]
Solving for eH, we have
- [math]\displaystyle{ E_H = \tfrac{1}{2} \frac{p_H \chi}{\rho_0} = \tfrac{1}{2} p_H (V_0 - V) }[/math]
With these expressions for pH and EH, the Grüneisen model on the Hugoniot becomes
- [math]\displaystyle{ p_H - p_0 = \frac{\Gamma}{V} \left(\frac{p_H \chi V_0}{2} - e_0\right) \quad \text{or} \quad \frac{\rho_0 C_0^2 \chi}{(1 - s\chi)^2}\left(1 - \frac{\chi}{2}\,\frac{\Gamma}{V}\,V_0\right) - p_0 = -\frac{\Gamma}{V} e_0 \,. }[/math]
If we assume that Γ/V = Γ0/V0 and note that [math]\displaystyle{ p_0 = -d e_0/d V }[/math], we get
- [math]\displaystyle{ (2) \qquad \frac{\rho C_0^2 \chi}{(1 - s\chi)^2}\left(1 - \frac{\Gamma_0\chi}{2}\right) + \frac{d e_0}{d V} + \frac{\Gamma_0}{V_0} e_0 = 0\,. }[/math]
The above ordinary differential equation can be solved for e0 with the initial condition e0 = 0 when V = V0 (χ = 0). The exact solution is
- [math]\displaystyle{ \begin{align} e_0 = \frac{\rho C_0^2 V_0}{2 s^4} \Biggl[&\exp(\Gamma_0\chi) (\tfrac{\Gamma_0}{s} - 3 ) s^2 - \frac{ [\tfrac{\Gamma_0}{s} - (3 - s\chi)]s^2}{1 - s\chi} + \\ & \exp\left[-\tfrac{\Gamma_0}{s} (1-s\chi)\right] (\Gamma_0^2 - 4 \Gamma_0 s + 2 s^2) (\text{Ei}[\tfrac{\Gamma_0}{s} (1-s\chi )] - \text{Ei}[\tfrac{\Gamma_0}{s}]) \Biggr] \end{align} }[/math]
where Ei[z] is the exponential integral. The expression for p0 is
- [math]\displaystyle{ \begin{align} p_0 = -\frac{de_0}{dV} = \frac{\rho C_0^2}{2s^4(1-\chi)} \Biggl[& \frac{s}{(1 - s\chi)^2} \Bigl (- \Gamma_0^2(1 - \chi)(1 -s\chi) + \Gamma_0 [s \{4 (\chi-1) \chi s-2 \chi+3\}-1] \\ & - \exp(\Gamma_0\chi)[\Gamma_0(\chi-1) -1](1-s\chi)^2(\Gamma_0-3s) + s [3-\chi s \{(\chi-2) s+4\}]\Bigr) \\ & - \exp\left[-\tfrac{\Gamma_0}{s} (1-s\chi)\right][\Gamma_0(\chi-1) - 1](\Gamma_0^2 - 4 \Gamma_0 s + 2 s^2)(\text{Ei}[\tfrac{\Gamma_0}{s} (1-s\chi )] - \text{Ei}[\tfrac{\Gamma_0}{s}]) \Biggr] \,. \end{align} }[/math]

For commonly encountered compression problems, an approximation to the exact solution is a power series solution of the form
- [math]\displaystyle{ e_0(V) = A + B \chi(V) + C \chi^2(V) + D \chi^3(V) + \dots }[/math]
and
- [math]\displaystyle{ p_0(V) = -\frac{de_0}{dV} = -\frac{de_0}{d\chi}\,\frac{d\chi}{dV} = \frac{1}{V_0}\,(B + 2C\chi + 3D\chi^2 + \dots) \,. }[/math]
Substitution into the Grüneisen model gives us the Mie–Grüneisen equation of state
- [math]\displaystyle{ p = \frac{1}{V_0}\,(B + 2C\chi + 3D\chi^2 + \dots) + \frac{\Gamma_0}{V_0} \left[e - (A + B \chi + C \chi^2 + D \chi^3 + \dots ) \right] \,. }[/math]
If we assume that the internal energy e0 = 0 when V = V0 (χ = 0) we have A = 0. Similarly, if we assume p0 = 0 when V = V0 we have B = 0. The Mie–Grüneisen equation of state can then be written as
- [math]\displaystyle{ p = \frac{1}{V_0}\left[2C\chi \left(1-\tfrac{\Gamma_0}{2}\chi\right) + 3D\chi^2\left(1 -\tfrac{\Gamma_0}{3}\chi\right) + \dots\right] + \Gamma_0 E }[/math]
where E is the internal energy per unit reference volume. Several forms of this equation of state are possible.
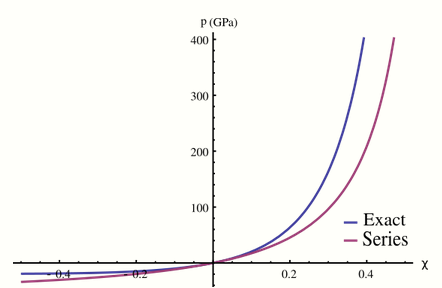
If we take the first-order term and substitute it into equation (2), we can solve for C to get
- [math]\displaystyle{ C = \frac{\rho_0 C_0^2 V_0}{2(1-s\chi)^2} \,. }[/math]
Then we get the following expression for p :
- [math]\displaystyle{ p = \frac{\rho_0 C_0^2 \chi}{(1-s\chi)^2} \left(1-\tfrac{\Gamma_0}{2}\chi\right) + \Gamma_0 E \,. }[/math]
This is the commonly used first-order Mie–Grüneisen equation of state .
References
- Mie, G. (1903) "Zur kinetischen Theorie der einatomigen Körper." Annalen der Physik 316.8, p. 657-697.
- Grüneisen, E. (1912). Theorie des festen Zustandes einatomiger Elemente. Annalen der Physik, 344(12), 257-306.
- Lemons, D. S., & Lund, C. M. (1999). Thermodynamics of high temperature, Mie–Gruneisen solids. American Journal of Physics, 67, 1105.
- Zocher, M.A.; Maudlin, P.J. (2000), "An evaluation of several hardening models using Taylor cylinder impact data", Conference: COMPUTATIONAL METHODS IN APPLIED SCIENCES AND ENGINEERING, BARCELONA (ES), 09/11/2000--09/14/2000, http://www.osti.gov/energycitations/product.biblio.jsp?osti_id=764004, retrieved 2009-05-12
- Wilkins, M.L. (1999), Computer simulation of dynamic phenomena, https://books.google.com/books?hl=en, retrieved 2009-05-12
- Mitchell, A.C.; Nellis, W.J. (1981), "Shock compression of aluminum, copper, and tantalum", Journal of Applied Physics 52 (5): 3363, doi:10.1063/1.329160, Bibcode: 1981JAP....52.3363M, http://link.aip.org/link/?JAPIAU/52/3363/1, retrieved 2009-05-12
- MacDonald, R.A.; MacDonald, W.M. (1981), "Thermodynamic properties of fcc metals at high temperatures", Physical Review B 24 (4): 1715–1724, doi:10.1103/PhysRevB.24.1715, Bibcode: 1981PhRvB..24.1715M https://dx.doi.org/10.1103%2FPhysRevB.24.1715




