
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Chenyu Hu | -- | 2564 | 2022-11-09 07:58:18 | | | |
| 2 | Catherine Yang | -1 word(s) | 2563 | 2022-11-14 04:11:38 | | | | |
| 3 | Catherine Yang | + 62 word(s) | 2625 | 2022-11-14 04:15:51 | | | | |
| 4 | Chenyu Hu | Meta information modification | 2625 | 2022-11-14 08:37:09 | | |
Video Upload Options
To understand, study, and optimize optical imaging systems from the information-theoretic viewpoint has been an important research subfield. However, the "direct point-to-point" image information acquisition mode of traditional optical imaging is lacking in "Coding-decoding" operation on the image information, and limits the development of further imaging capabilities. On the other hand, ghost imaging (GI) systems, combined with modern light-field modulation and digital photoelectric detection technologies, behave more in line with the modulation–demodulation information transmission mode compared to traditional optical imaging. This puts forward imperative demands and challenges for understanding and optimizing ghost imaging systems from the viewpoint of information theory, as well as bringing more development opportunities for the research field of information optical imaging. Here, several specific GI systems and studies with various extended imaging capabilities will be briefly reviewed.
1. Mapping Higher-Dimensional Light-Field Information into Lower-Dimensional Domain
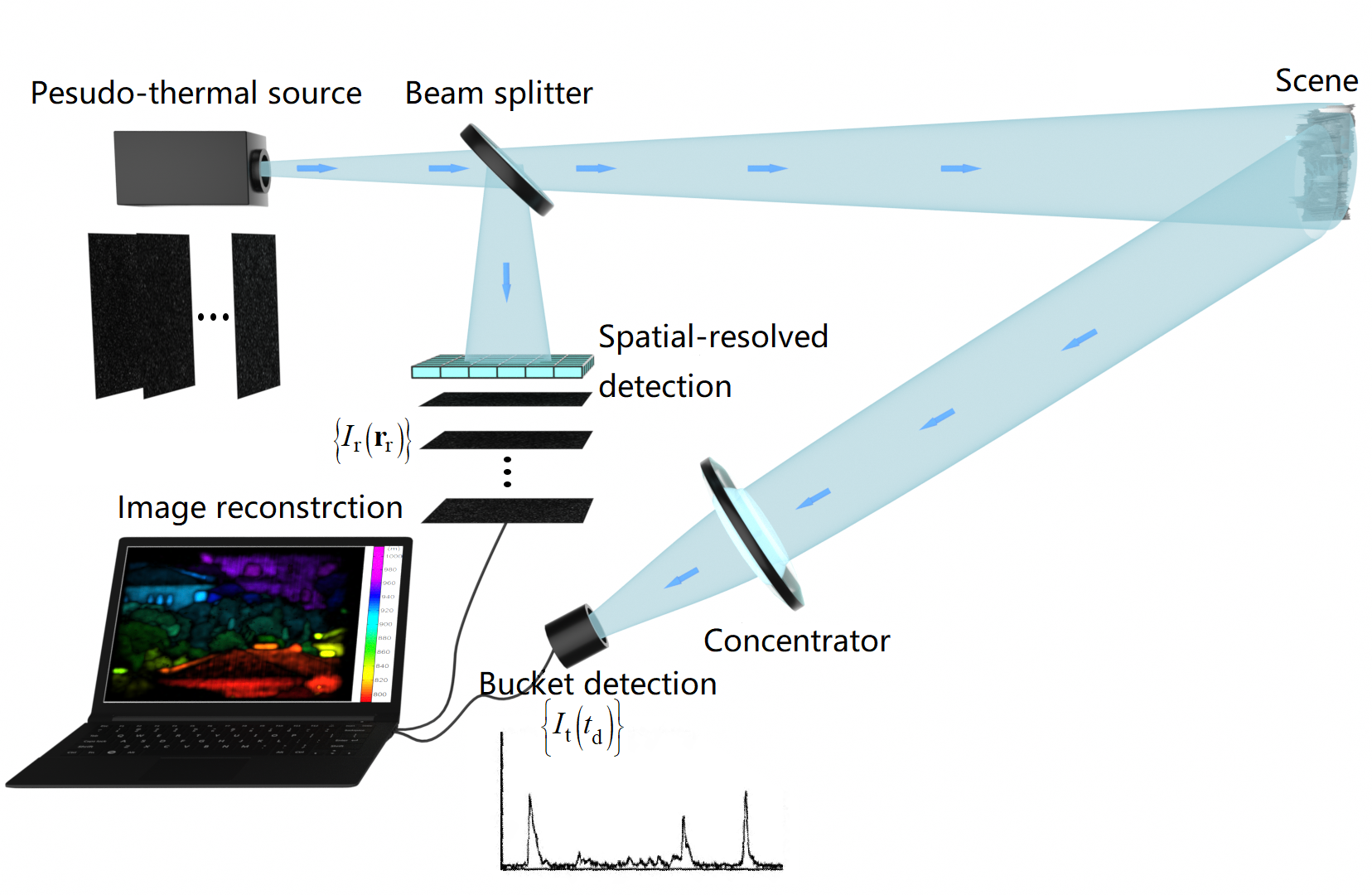
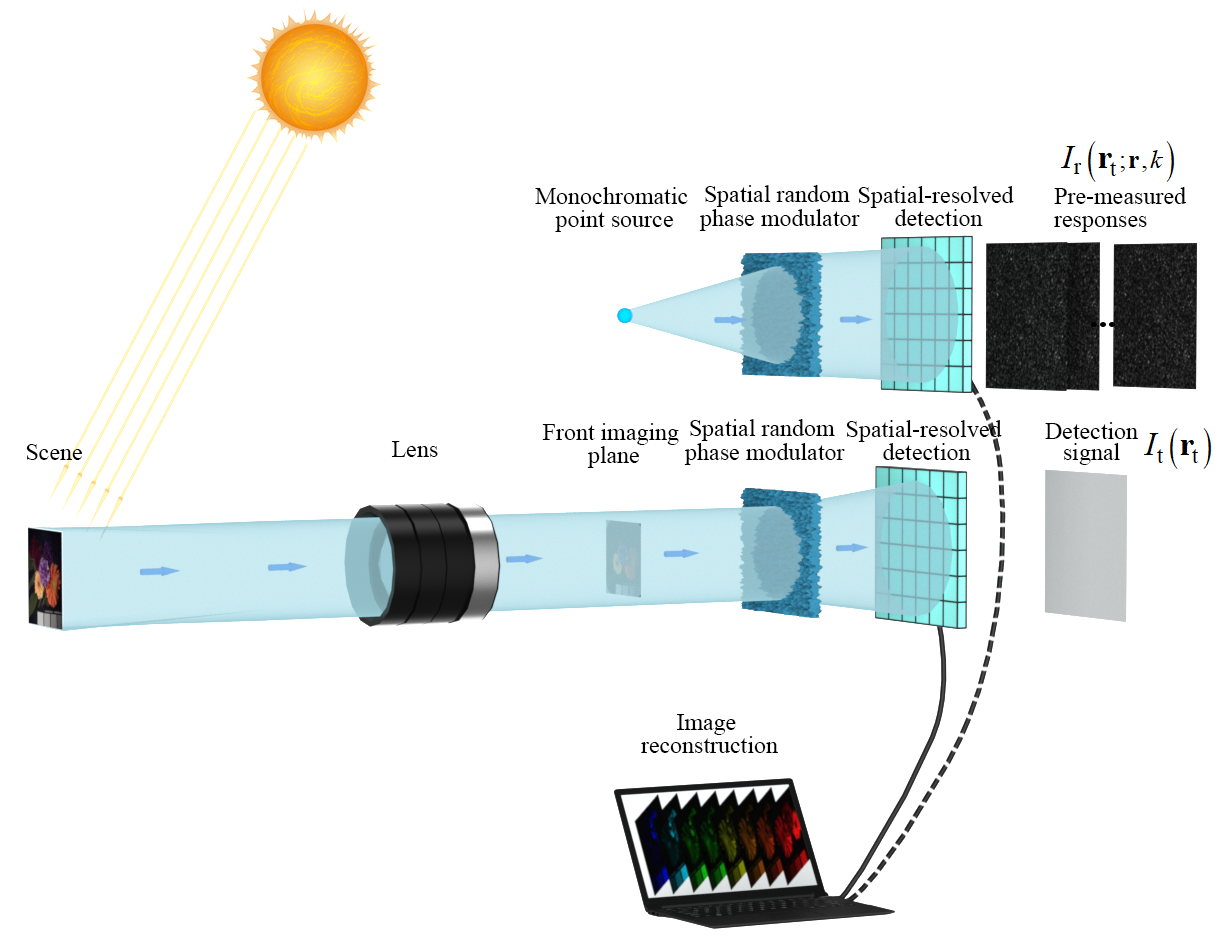
2. Resolution Analysis in the High-Dimensional Light-Field Domain
3. Optimizing the Encoding Mode to Reduce Unnecessary Sampling Redundancy
4. Task-Oriented GI System Design
5. X-ray Diffraction GI
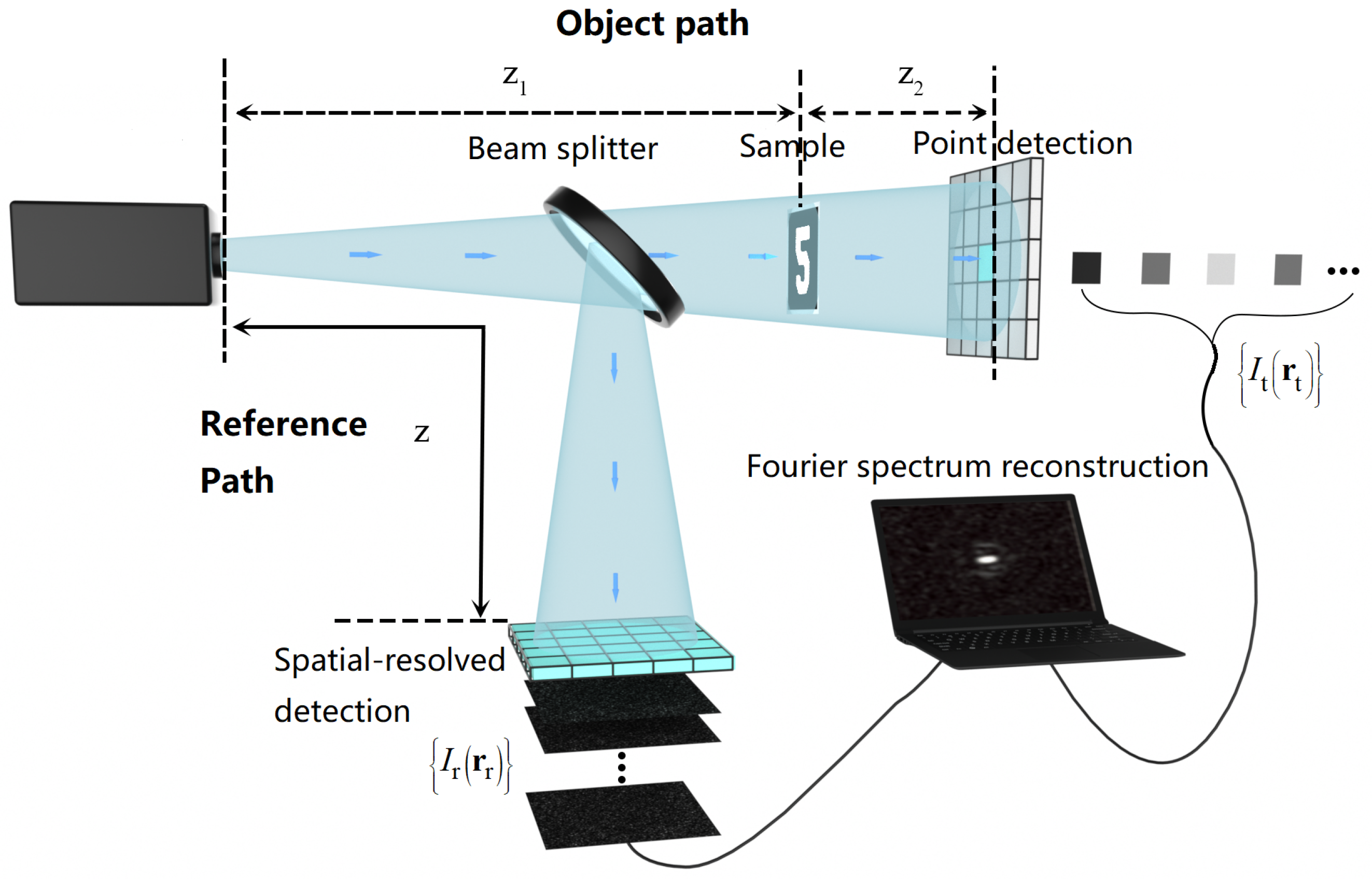
References
- Zhao, C.; Gong, W.; Chen, M.; Li, E.; Wang, H.; Xu, W.; Han, S. Ghost imaging lidar via sparsity constraints. Appl. Phys. Lett. 2012, 101, 141123.
- Gong, W. Theoretical and Experimental Investigation On Ghost Imaging Radar with Thermal Light. Ph.D. Thesis, Shanghai Institute of Optics and Fine Mechanics, Chinese Academy of Sciences, Shanghai, China, 2011.
- Gong, W.; Zhao, C.; Yu, H.; Chen, M.; Xu, W.; Han, S. Three-dimensional ghost imaging lidar via sparsity constraint. Sci. Rep. 2016, 6, 1–6.
- Wang, C.; Mei, X.; Pan, L.; Wang, P.; Li, W.; Gao, X.; Bo, Z.; Chen, M.; Gong, W.; Han, S. Airborne near infrared three-dimensional ghost imaging lidar via sparsity constraint. Remote. Sens. 2018, 10, 732.
- Ma, Y.; He, X.; Meng, Q.; Liu, B.; Wang, D. Microwave staring correlated imaging and resolution analysis. In Geo-Informatics in Resource Management and Sustainable Ecosystem; Springer: Berlin, Germany, 2013; pp. 737–747.
- Li, D.; Li, X.; Qin, Y.; Cheng, Y.; Wang, H. Radar coincidence imaging: An instantaneous imaging technique with stochastic signals. IEEE Trans. Geosci. Remote. Sens. 2013, 52, 2261–2277.
- Cheng, Y.; Zhou, X.; Xu, X.; Qin, Y.; Wang, H. Radar coincidence imaging with stochastic frequency modulated array. IEEE J. Sel. Top. Signal Process. 2016, 11, 414–427.
- Kikuchi, K. Fundamentals of coherent optical fiber communications. J. Light. Technol. 2015, 34, 157–179.
- Secondini, M.; Foggi, T.; Fresi, F.; Meloni, G.; Cavaliere, F.; Colavolpe, G.; Forestieri, E.; Poti, L.; Sabella, R.; Prati, G. Optical time–frequency packing: Principles, design, implementation, and experimental demonstration. J. Light. Technol. 2015, 33, 3558–3570.
- Deng, C.; Gong, W.; Han, S. Pulse-compression ghost imaging lidar via coherent detection. Opt. Express 2016, 24, 25983–25994.
- Pan, L.; Wang, Y.; Deng, C.; Gong, W.; Bo, Z.; Han, S. Micro-Doppler effect based vibrating object imaging of coherent detection GISC lidar. Opt. Express 2021, 29, 43022–43031.
- Gong, W.; Sun, J.; Deng, C.; Lu, Z.; Zhou, Y.; Han, S. Research progress on single-pixel imaging lidar via coherent detection. Laser Optoelectron. Prog. 2021, 58, 1011003.
- Liu, Z.; Tan, S.; Wu, J.; Li, E.; Shen, X.; Han, S. Spectral camera based on ghost imaging via sparsity constraints. Sci. Rep. 2016, 6, 25718.
- Giglio, M.; Carpineti, M.; Vailati, A. Space intensity correlations in the near field of the scattered light: A direct measurement of the density correlation function g (r). Phys. Rev. Lett. 2000, 85, 1416.
- Cerbino, R.; Peverini, L.; Potenza, M.; Robert, A.; Bösecke, P.; Giglio, M. X-ray-scattering information obtained from near-field speckle. Nat. Phys. 2008, 4, 238–243.
- Chu, C.; Liu, S.; Liu, Z.; Hu, C.; Zhao, Y.; Han, S. Spectral polarization camera based on ghost imaging via sparsity constraints. Appl. Opt. 2021, 60, 4632–4638.
- Liu, S.; Liu, Z.; Hu, C.; Li, E.; Shen, X.; Han, S. Spectral ghost imaging camera with super-Rayleigh modulator. Opt. Commun. 2020, 472, 126017.
- Wang, P.; Liu, Z.; Wu, J.; Shen, X.; Han, S. Dispersion control of broadband super-Rayleigh speckles for snapshot spectral ghost imaging. Chin. Opt. Lett. 2022, 20, 091102.
- Liu, Z.; Hu, C.; Tong, Z.; Chu, C.; Han, S. Some research progress on the theoretical study of ghost imaging in Shanghai Institute of Optics and Fine Mechanics, Chinese Academy of Sciences. Infrared Laser Eng. 2021, 50, 20211059.
- Tong, Z.; Liu, Z.; Wang, J. Spatial resolution limit of ghost imaging camera via sparsity constraints-break Rayleigh’s criterion based on the discernibility in high-dimensional light field space. arXiv 2020, arXiv:2004.00135.
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306.
- Candès, E.J.; Tao, T. Near-optimal signal recovery from random projections: Universal encoding strategies? IEEE Trans. Inf. Theory 2006, 52, 5406–5425.
- Tropp, J.A. Greed is good: Algorithmic results for sparse approximation. IEEE Trans. Inf. Theory 2004, 50, 2231–2242.
- Sekko, E.; Thomas, G.; Boukrouche, A. A deconvolution technique using optimal Wiener filtering and regularization. Signal Process. 1999, 72, 23–32.
- Orieux, F.; Giovannelli, J.F.; Rodet, T. Bayesian estimation of regularization and point spread function parameters for Wiener–Hunt deconvolution. JOSA A 2010, 27, 1593–1607.
- Jin, A.; Yazici, B.; Ale, A.; Ntziachristos, V. Preconditioning of the fluorescence diffuse optical tomography sensing matrix based on compressive sensing. Opt. Lett. 2012, 37, 4326–4328.
- Yao, R.; Pian, Q.; Intes, X. Wide-field fluorescence molecular tomography with compressive sensing based preconditioning. Biomed. Opt. Express 2015, 6, 4887–4898.
- Tong, Z.; Wang, F.; Hu, C.; Wang, J.; Han, S. Preconditioned generalized orthogonal matching pursuit. EURASIP J. Adv. Signal Process. 2020, 2020, 1–14.
- Tong, Z.; Liu, Z.; Hu, C.; Wang, J.; Han, S. Preconditioned deconvolution method for high-resolution ghost imaging. Photonics Res. 2021, 9, 1069–1077.
- Li, E.; Chen, M.; Gong, W.; Yu, H.; Han, S. Mutual information of ghost imaging systems. Acta Opt. Sin. 2013, 33, 1211003.
- Xu, X.; Li, E.; Shen, X.; Han, S. Optimization of speckle patterns in ghost imaging via sparse constraints by mutual coherence minimization. Chin. Opt. Lett. 2015, 13, 071101.
- Candès, E.J.; Romberg, J. Sparsity and incoherence in compressive sampling. Inverse Probl. 2007, 23, 969.
- Aharon, M.; Elad, M.; Bruckstein, A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal Process. 2006, 54, 4311–4322.
- Sulam, J.; Ophir, B.; Zibulevsky, M.; Elad, M. Trainlets: Dictionary learning in high dimensions. IEEE Trans. Signal Process. 2016, 64, 3180–3193.
- Hu, C.; Tong, Z.; Liu, Z.; Huang, Z.; Wang, J.; Han, S. Optimization of light fields in ghost imaging using dictionary learning. Opt. Express 2019, 27, 28734–28749.
- Aβmann, M.; Bayer, M. Compressive adaptive computational ghost imaging. Sci. Rep. 2013, 3, 1545.
- Yu, W.K.; Li, M.F.; Yao, X.R.; Liu, X.F.; Wu, L.A.; Zhai, G.J. Adaptive compressive ghost imaging based on wavelet trees and sparse representation. Opt. Express 2014, 22, 7133–7144.
- Li, Z.; Suo, J.; Hu, X.; Dai, Q. Content-adaptive ghost imaging of dynamic scenes. Opt. Express 2016, 24, 7328–7336.
- Liu, B.; Wang, F.; Chen, C.; Dong, F.; McGloin, D. Self-evolving ghost imaging. Optica 2021, 8, 1340–1349.
- Fisher, R.A. On the mathematical foundations of theoretical statistics. Philos. Trans. R. Soc. London. Ser. Contain. Pap. Math. Phys. Character 1922, 222, 309–368.
- Hu, C.; Zhu, R.; Yu, H.; Han, S. Correspondence Fourier-transform ghost imaging. Phys. Rev. 2021, 103, 043717.
- Luo, K.H.; Huang, B.Q.; Zheng, W.M.; Wu, L.A. Nonlocal imaging by conditional averaging of random reference measurements. Chin. Phys. Lett. 2012, 29, 074216.
- Sun, M.J.; Meng, L.T.; Edgar, M.P.; Padgett, M.J.; Radwell, N. A Russian Dolls ordering of the Hadamard basis for compressive single-pixel imaging. Sci. Rep. 2017, 7, 3464.
- Yu, W.K. Super sub-Nyquist single-pixel imaging by means of cake-cutting Hadamard basis sort. Sensors 2019, 19, 4122.
- Yu, W.K.; Liu, Y.M. Single-pixel imaging with origami pattern construction. Sensors 2019, 19, 5135.
- Neifeld, M.A.; Ashok, A.; Baheti, P.K. Task-specific information for imaging system analysis. JOSA A 2007, 24, B25–B41.
- Buzzi, S.; Lops, M.; Venturino, L. Track-before-detect procedures for early detection of moving target from airborne radars. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 937–954.
- Zhai, X.; Cheng, Z.; Wei, Y.; Liang, Z.; Chen, Y. Compressive sensing ghost imaging object detection using generative adversarial networks. Opt. Eng. 2019, 58, 013108.
- Chen, H.; Shi, J.; Liu, X.; Niu, Z.; Zeng, G. Single-pixel non-imaging object recognition by means of Fourier spectrum acquisition. Opt. Commun. 2018, 413, 269–275.
- Zhang, Z.; Li, X.; Zheng, S.; Yao, M.; Zheng, G.; Zhong, J. Image-free classification of fast-moving objects using “learned” structured illumination and single-pixel detection. Opt. Express 2020, 28, 13269–13278.
- Liu, X.F.; Yao, X.R.; Lan, R.M.; Wang, C.; Zhai, G.J. Edge detection based on gradient ghost imaging. Opt. Express 2015, 23, 33802–33811.
- Wang, L.; Zou, L.; Zhao, S. Edge detection based on subpixel-speckle-shifting ghost imaging. Opt. Commun. 2018, 407, 181–185.
- Yang, D.; Chang, C.; Wu, G.; Luo, B.; Yin, L. Compressive ghost imaging of the moving object using the low-order moments. Appl. Sci. 2020, 10, 7941.
- Sun, S.; Gu, J.H.; Lin, H.Z.; Jiang, L.; Liu, W.T. Gradual ghost imaging of moving objects by tracking based on cross correlation. Opt. Lett. 2019, 44, 5594–5597.
- Zhang, M.; Wei, Q.; Shen, X.; Liu, Y.; Liu, H.; Cheng, J.; Han, S. Lensless Fourier-transform ghost imaging with classical incoherent light. Phys. Rev. 2007, 75, 021803.
- Zhang, M. Experimental Investigation on Non-local Lensless Fourier-transfrom imaging with Cassical Incoherent Light. Ph.D. Thesis, Shanghai Institute of Optics and Fine Mechanics, Chinese Academy of Sciences, Shanghai, China, 2007.
- Yu, H.; Lu, R.; Han, S.; Xie, H.; Du, G.; Xiao, T.; Zhu, D. Fourier-transform ghost imaging with hard X rays. Phys. Rev. Lett. 2016, 117, 113901.
- Liu, H.; Cheng, J.; Han, S. Ghost imaging in Fourier space. J. Appl. Phys. 2007, 102, 103102.
- Tan, Z.; Yu, H.; Lu, R.; Zhu, R.; Han, S. Non-locally coded Fourier-transform ghost imaging. Opt. Express 2019, 27, 2937–2948.
- Zhu, R.; Yu, H.; Tan, Z.; Lu, R.; Han, S.; Huang, Z.; Wang, J. Ghost imaging based on Y-net: A dynamic coding and decoding approach. Opt. Express 2020, 28, 17556–17569.




