
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Camila Xu | -- | 4319 | 2022-11-04 01:51:53 |
Video Upload Options
Biology Monte Carlo methods (BioMOCA) have been developed at the University of Illinois at Urbana-Champaign to simulate ion transport in an electrolyte environment through ion channels or nano-pores embedded in membranes. It is a 3-D particle-based Monte Carlo simulator for analyzing and studying the ion transport problem in ion channel systems or similar nanopores in wet/biological environments. The system simulated consists of a protein forming an ion channel (or an artificial nanopores like a Carbon Nano Tube, CNT), with a membrane (i.e. lipid bilayer) that separates two ion baths on either side. BioMOCA is based on two methodologies, namely the Boltzmann transport Monte Carlo (BTMC) and particle-particle-particle-mesh (P3M). The first one uses Monte Carlo method to solve the Boltzmann equation, while the later splits the electrostatic forces into short-range and long-range components.
1. Backgrounds
In full-atomic molecular dynamics simulations of ion channels, most of the computational cost is for following the trajectory of water molecules in the system. However, in BioMOCA the water is treated as a continuum dielectric background media. In addition to that, the protein atoms of the ion channel are also modeled as static point charges embedded in a finite volume with a given dielectric coefficient. So is the lipid membrane, which is treated as a static dielectric region inaccessible to ions. In fact the only non-static particles in the system are ions. Their motion is assumed classical, interacting with other ions through electrostatic interactions and pairwise Lennard-Jones potential. They also interact with the water background media, which is modeled using a scattering mechanism.
The ensemble of ions in the simulation region, are propagated synchronously in time and 3-D space by integrating the equations of motion using the second-order accurate leap-frog scheme. Ion positions r and forces F are defined at time steps t, and t + dt. The ion velocities are defined at t – dt/2, t + dt/2. The governing finite difference equations of motion are
- [math]\displaystyle{ \vec{v}(t+\frac{dt}{2}) = \vec{v}(t-\frac{dt}{2}) + \vec{F}(t) \, dt }[/math]
- [math]\displaystyle{ \vec{r}(t+dt)= \vec{r}(t-dt) + \vec{v}(t+\frac{dt}{2}) \, dt }[/math]
where F is the sum of electrostatic and pairwise ion-ion interaction forces.
1.1. Electrostatic Field Solution
The electrostatic potential is computed at regular time intervals by solving the Poisson’s equation
- [math]\displaystyle{ \nabla (\varepsilon (r)\nabla \phi (r,t)) = -(\rho_\text{ions}(r,t) + \rho_\text{perm}(r)) }[/math]
where [math]\displaystyle{ \rho_\text{ions}(r,t) }[/math] and [math]\displaystyle{ \rho_\text{perm}(r) }[/math] are the charge density of ions and permanent charges on the protein, respectively. [math]\displaystyle{ \epsilon (r) }[/math] is the local dielectric constant or permittivity, and [math]\displaystyle{ \phi (r,t) }[/math] is the local electrostatic potential. Solving this equation provides a self-consistent way to include applied bias and the effects of image charges induced at dielectric boundaries.
The ion and partial charges on protein residues are assigned to a finite rectangular grid using the cloud-in-cell (CIC) scheme.[1] Solving the Poisson equation on the grid counts for the particlemesh component of the P3M scheme. However, this discretization leads to an unavoidable truncation of the short-range component of electrostatic force, which can be corrected by computing the short-range charge-charge Coulombic interactions.
1.2. Dielectric Coefficient
Assigning the appropriate values for dielectric permittivity of the protein, membrane, and aqueous regions is of great importance. The dielectric coefficient determines the strength of the interactions between charged particles and also the dielectric boundary forces (DBF) on ions approaching a boundary between two regions of different permittivity. However, in nano scales the task of assigning specific permittivity is problematic and not straightforward.
The protein or membrane environment could respond to an external field in a number of different ways.[2][3][4][5][6] Field induced dipoles, reorientation of permanent dipoles, protonation and deprotonation of protein residues, larger scale reorganization of ionized side-chains and water molecules, both within the interior and on the surface of the protein, are all examples of how complicated the assignment of permittivity is. In MD simulations, where all the charges, dipoles, and field induced atomic dipoles are treated explicitly then it is suggested that a dielectric value of 1 is appropriate. However, in reduced-particle ion simulation programs, such as ours, where the protein, membrane, and water are continuum backgrounds and treated implicitly, and on top of that, the ion motion takes place on the same time-scale as the protein’s response to its presence, it is very difficult to assign the dielectric coefficients. In fact, changing the dielectric coefficients could easily alter the channel characteristics, such as ion permeation and selectivity The assignment of dielectric coefficient for water is another key issue. The water molecules inside ion channels could be very ordered due to tapered size of the pore, which is often lined with highly charged residues, or hydrogen bond formation between water molecules and protein.[7] As a result, the dielectric constant of water inside an ion channel could be quite different from the value under bulk conditions. To make the matter even more complicated, the dielectric coefficients of water inside nanopores is not necessarily an isotropic scalar value, but an anisotropic tensor having different values in different directions.
1.3. Anisotropic Permittivity
It has become evident that the macroscopic properties of a system do not necessarily extend to the molecular length scales. In a recent research study carried by Reza Toghraee, R. Jay Mashl, and Eric Jakobsson at the University of Illinois, Urbana-Champaign,[3] they used Molecular Dynamics simulations to study the properties of water in featureless hydrophobic cylinders with diameters ranging from 1 to 12 nm. This study showed that water undergoes distinct transitions in structure, dielectric properties, and mobility as the tube diameter is varied. In particular they found that the dielectric properties in the range of 1 to 10 nm is quite different from bulk water and is in fact anisotropic in nature. Though, such featureless hydrophobic channels do not represent actual ion channels and more research has to be done in this area before one could use such data for ion channels, it is evident that water properties like permittivity inside an ion channel or nano-pore could be much more complicated that it has been thought before. While a high axial dielectric constant shields ion’s electrostatic charges in the axial direction (along the channel), low radial dielectric constant increases the interaction between the mobile ion and the partial charges, or the dielectric charge images on the channel, conveying stronger selectivity in ion channels.
Solving the Poisson equation based on an anisotropic permittivity has been incorporated into BioMOCA using the box integration discretization method,[8] which has been briefly described below.
2. Calculations
2.1. Box Integration Discretization
In order to use box integration for discretizing a D-dimensional Poisson equation
- [math]\displaystyle{ \nabla (\varepsilon \nabla \varphi) = \rho }[/math]
with [math]\displaystyle{ \varepsilon }[/math] being a diagonal D × D tensor, this differential equation is reformulated as an integral equation. Integration the above equation over a D-dimensional region [math]\displaystyle{ \Omega }[/math], and using Gauss theorem, then the integral formulation is obtained
- [math]\displaystyle{ \oint_{\partial \Omega} \hat{n} (\varepsilon \nabla \varphi) = - \int_\Omega \rho }[/math]
In this appendix it is assumed to be a two-dimensional case. Upgrading to a three-dimensional system would be straightforward and legitimate as the Gauss theorem is also valid for the one and three dimensions. [math]\displaystyle{ \epsilon }[/math] is assumed to be given on the rectangular regions between nodes, while [math]\displaystyle{ \varphi }[/math] is defined on the grid nodes (as illustrated on figure at the right).
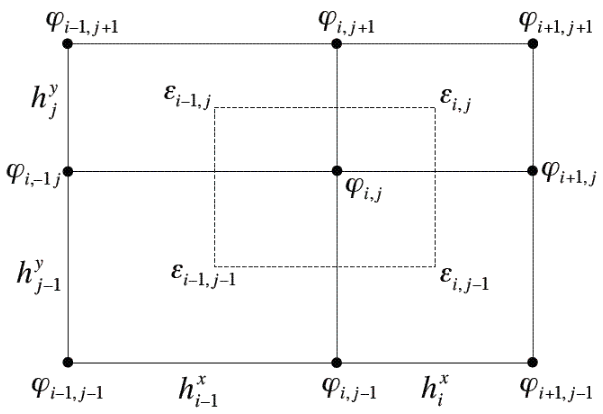
The integration regions [math]\displaystyle{ \Omega }[/math] are then chosen as rectangles centered around node and extending to the 4 nearest neighbor nodes. The gradient [math]\displaystyle{ \nabla \varphi }[/math] is then approximated using centered difference normal to the boundary of the integration region [math]\displaystyle{ \Omega }[/math], and average [math]\displaystyle{ \epsilon }[/math] over the integration surface [math]\displaystyle{ \partial \Omega }[/math] . This approach allows us to approximate the left hand side of the Poisson equation above in first order as
- [math]\displaystyle{ \oint_{\partial \Omega} \hat{n}(\varepsilon \nabla \varphi) = \frac{\varphi_{i+1,j} - \varphi_{i,j}}{h_i^x} \left ( \frac{h^y_j}{2} \epsilon^x_{i,j} + \frac{h^y_{j-1}}{2} \varepsilon^x_{i,j-1} \right ) }[/math]
- [math]\displaystyle{ {} - \frac{\varphi_{i,j} - \varphi_{i-1,j}}{h_{i-1}^x} \left ( \frac{h^y_j}{2} \epsilon^x_{i-1,j} + \frac{h^y_{j-1}}{2} \varepsilon^x_{i-1,j-1} \right ) }[/math]
- [math]\displaystyle{ {} + \frac{\varphi_{i,j+1} - \varphi_{i,j}}{h_{j}^y} \left ( \frac{h^x_i}{2} \varepsilon^y_{i,j} + \frac{h^x_{i-1}}{2} \varepsilon^y_{i-1,j} \right ) }[/math]
- [math]\displaystyle{ {} - \frac{\varphi_{i,j} - \varphi_{i,j-1}}{h_{j-1}^y} \left ( \frac{h^x_i}{2} \varepsilon^y_{i,j-1} + \frac{h^x_{i-1}}{2} \varepsilon^y_{i-1,j-1} \right ) }[/math]
where [math]\displaystyle{ \varepsilon^x }[/math] and [math]\displaystyle{ \varepsilon^y }[/math] are the two components of the diagonal of the tensor [math]\displaystyle{ \epsilon }[/math]. Discretizing the right-hand side of the Poisson equation is fairly simple. [math]\displaystyle{ \rho }[/math] is discretized on the same grid nodes, as it's been done for [math]\displaystyle{ \varphi }[/math].
- [math]\displaystyle{ \int_{\Omega_i} \rho = \text{Volume}(\Omega_i) \rho_i }[/math]
2.2. Ion Size
The finite size of ions is accounted for in BioMOCA using pairwise repulsive forces derived from the 6–12 Lennard-Jones potential. A truncated-shifted form of the Lennard-Jones potential is used in the simulator to mimic ionic core repulsion. The modified form of the Lennard-Jones pairwise potential that retains only the repulsive component is given by
- [math]\displaystyle{ U_{LJ}(r_{ij}) = \begin{cases} 4\epsilon_{LJ} \left (\left (\frac{\sigma_{ij}}{r_{ij}}\right )^{12} - \left (\frac{\sigma_{ij}}{r_{ij}}\right )^6 \right ) + \epsilon_{LJ} & r_{ij} \lt 2^{1/6} \sigma_{ij} \\ 0 & r_{ij} \gt 2^{1/6} \sigma_{ij} \end{cases} }[/math]
Here, [math]\displaystyle{ \epsilon_{LJ} }[/math] is the Lennard-Jones energy parameter and [math]\displaystyle{ \sigma_{ij}=(\sigma_i + \sigma_j)/2 }[/math] is the average of the individual Lennard-Jones distance parameters for particles i and j. Using a truncated form of the potential is computationally efficient while preventing the ions from overlapping or coalescing, something that would be clearly unphysical.
2.3. Ion-Protein Interaction
Availability of high-resolution X-ray crystallographic measurements of complete molecular structures provides information about the type and location of all atoms that forms the protein. In BioMOCA the protein atoms are modeled as static point charges embedded in a finite volume inaccessible to the ions and associated with a user-defined dielectric coefficient. Moreover, a number of force-field parameters are available that provide information about the charge and radii of atoms in different amino-acid groups. The conjunction of the molecular structure and force fields provide the coordinates, radii, and charge of each atom in the protein channel. BioMOCA uses such information in the standard PQR (Position-Charge-Radius) format to map the protein system onto a rectangular grid.
Ideally, the steric interactions between protein atoms and the ions in the aqueous medium are to use a repulsive potential like Lennard-Jones to prevent ions from penetrating the protein. As this approach could add a significant load to the amount of calculations, a simpler approach is chosen that treats the protein surfaces as predetermined hard wall boundaries. Many recent open source molecular biology packages have built-in facilities that determine the volume accessible to ions in a protein system. The Adaptive Poisson Boltzmann Solver (APBS) scheme[9] has been incorporated to BioMOCA to obtain the accessible volume region and therefore partition the simulation domain into continuous regions.
Ions are deemed to have access to protein and lipid regions and if any point within the finite-size of ionic sphere crosses the protein or membrane boundary, a collision is assumed and the ion is reflected diffusively.
2.4. Ion-Water Interactions
As a reduced particle approach, BioMOCA replaces the explicit water molecules with continuum background and handles the ion-water interactions using BTMC method, in which, appropriate scattering rates should be chosen. In other words, ion trajectories are randomly interrupted by scattering events that account for the ions’ diffusive motion in water.[2] In between these scattering events, ions follow the Newtonian forces. The free flight times, Tf, are generated statistically from the total scattering rate according to
- [math]\displaystyle{ -\ln(r) = \int^{T_f}_0 \lambda (\vec{p}(t)) \, dt }[/math]
where r is a random number uniformly distributed on the unit interval. [math]\displaystyle{ \lambda }[/math], a function of momentum, is the total scattering rate for all collision mechanisms. At the end of each free flight, the ion’s velocity is reselected randomly from a Maxwellian distribution. As the correct scattering mechanism for ion-water interactions in nonbulk electrolyte solutions has yet to be developed, a position dependent scattering rate linked to the local diffusivity is used in our model. This dependency on position comes from the fact that water molecules can have different order of organization in different regions, which will affect the scattering rate.
2.5. Position-Dependent Diffusivity
It is widely accepted that the ions and water molecules do not have the same mobility or diffusivity in confined regions as in bulk.[5][10] In fact, it is more likely to have a lessening in the effective mobility of ions in ion channels.[4] In reduced particle methods where the channel water is assumed as implicit continuum background, a mean ion mobility is needed to reveal how ions could diffuse due to local electrostatic forces and random events. In Transport Monte Carlo simulations, the total scattering rate ([math]\displaystyle{ \lambda }[/math]), is assumed to only result from ion-water interactions; it is related to ion diffusivity with the expression
- [math]\displaystyle{ \lambda = \frac{kT}{mD} }[/math]
where m is the mass of the ion and D is its diffusion constant. As the equation indicates, reduced diffusivity of ions inside the lumen of the channel renders to increased incidence of scattering events.
2.6. Hydration Shells
In addition to having a diffusive effect on ion transport, water molecules also form hydration shells around individual ions due to their polar nature. The hydration shell not only shields the charge on ions from other ions but also modulates the ion radial distribution function causing the formation of peaks and troughs. The average minimum distance between two ions is increased as there is always at least one layer of water molecules present between them, acting as a physical deterrent preventing two ions from getting too close to each other, in a manner that is similar to the short-range repulsive component of the Lennard-Jones potential.
The theory of hydration shells is well developed in the physical chemistry literature however a simple model is required that captures the essential effects with as little computational overhead as possible. For this purpose the same pairwise potential discussed by Im and Roux[11] is implemented to include the effect of hydration shells.
- [math]\displaystyle{ U_{hy} = c_0 \exp \left (\frac{c_1 - r}{c_2} \right ) cos(c_3(c_1 - r)\pi ) + c_4 \left (\frac{c_1}{r} \right )^6 }[/math]
The coefficients ci were determined empirically for a 1 M KCl solution, using MD simulations to benchmark the ion radial distribution functions against Equilibrium Monte Carlo simulations. The effect of hydration shells was found to be important in simulations at higher salt concentrations where the conductance of many ion channels, porin among them, is observed to saturate as the salt concentration in the electrolyte baths is further increased. Earlier simulations that did not include a model of hydration shells did not reproduce the conductance saturation behavior. This suggests an additional repulsive potential acting to prevent ion crowding, and hence limiting the concentration of ions and current density in the confined space of the pore even at high bath salt concentration. When the repulsive potential was included moderate channel conductance was observed.
3. Conditions and Methods
3.1. Boundary Conditions
The electrical and physiological properties of ion channels are experimentally measured by inserting the channel into a lipid membrane separating two baths containing solutions of specific concentrations. A constant electrostatic bias is applied across the channel by immersing the electrodes in the two baths. Formulating boundary conditions that accurately represent these contact regions may require enormously large bath regions and is a challenging task. Beyond a Debye length from the membrane the electrostatic potential and ion densities do not vary appreciably. This assumption has been supported by the results of continuum results presented earlier.[12] For typical salt concentrations used in ion channel simulations, the Debye length is of the order of 10 Å. Using the assumption, Dirichlet boundary conditions are imposed on the potential at the two domain boundary planes that are transverse to the channel, taking care that these planes are sufficiently far from the membrane.
The other problem in duplicating the experimental conditions is the problem of maintaining fixed charge density in the two baths. This problem is treated by maintaining the specified density in two buffer regions extending from the boundary plane toward the membrane. The number of ions needed to maintain the density in the two buffer regions is calculated at the start of the simulations. The count of the ions in these buffers is sampled throughout the simulation and an ion is injected whenever a deficit is observed. The initial velocity of the injected particle is decided according to Maxwellian distribution. The ions can leave the system only by exiting through the two Dirichlet boundary planes and an ion is not removed artificially from these buffer regions. The reflections from the Neumann boundary planes are treated as elastic reflections.
3.2. Multi-Grids and Grid Focusing Method
In all most any of the methods in simulation of ion channels, the major computational cost comes from the calculation of electrostatic forces acting on the ions. In continuum models, for instance, where ionic density exist rather than explicit ions, the electrostatic potential is calculated in a self-consistent manner by solving the Poisson equation. In MD simulations, on the other hand, the electrostatic forces acting on the particles are calculated by explicit evaluation of the Coulombic force term, often splitting the short-range and long-range electrostatic forces so they could be computed with different methods. In a model such as a reduced particle method, the longrange electrostatic forces are evaluated by solving the Poisson equation and augmenting the forces so obtained with a short-range component. By solving the Poisson equation it is possible to self-consistently include the forces arising from the bias to the system, while this is a difficult issue to be addressed in MD simulations.
Currently there are two Poisson solvers implemented in BioMOCA based on the finite difference method. One uses the pre-conditioned Conjugate Gradient scheme (pCG) and is used by default. The later is borrowed from an APBS solver, which uses a V-multi-grid scheme. Other than the numerical approach to solve the Poisson equation, the main difference between the two solvers is on how they address the permittivity in the system. In the first solver, a dielectric value is assigned to each cell in the grid, while in the APBS solver the dielectric coefficients are defined on the grid nodes. As discussed earlier box integration method is used in the pCG solver, which treats the Poisson equation in the most accurate way. Even though a full multigrid solver based on box-integration method has been under development, there is a neat way to reuse the already exiting code and treat the ion channel systems.
Ion channel simulations require the presence of large bath regions for accurate treatment of screening.[2] There being of such bath regions make the mesh domain of Poisson equation large and leads to either a large number of grid points with fine mesh resolution or a small number of grid points with very coarse discretization. From bulk simulations a coarse mesh is sufficient for describing the baths using the P3M scheme. However, a fine resolution is required in the channel domain because of the highly charged nature of these regions and the presence of spatially varying dielectric regions. Besides the ultimate interest is to study the channel behavior in terms of ion permeability, selectivity, gating, density, etc.... In other words, it is better off to put more computational resources in the channel region, and bare minimum in the baths to reduce the overall computational cost and speed up of simulations from weeks to perhaps days instead. A scheme based on the grid focusing method has been developed that makes it possible to satisfy the requirement of large bath region and a fine grid resolution in channel at the same time in a computationally effective way. This methodology is capable to have multiple fine mesh domains, which may be needed to describe multiple pore channels like OmpF porin, or an array of ion channels sharing the same bath regions or even having yet finer meshes inside a fine mesh for relatively large channels with narrow ion passages like Nicotine receptor channel.[13]
The first grid is coarse mesh spanning the entire problem domain including the bath regions and the channel region. The second grid (and so on for any other grids, 3rd, 4th, etc.) is a relatively much finer mesh that spans a sub-domain of the system containing the region that requires fine resolution like the channel pore. The Poisson equation is first solved on the coarse mesh with all the Dirichlet and Neumann boundary conditions, taking into account the applied bias. Next the boundary conditions for the secondary meshes are obtained by interpolating from the first or previous solutions of the Poisson equation. The Poisson equation is solved again for the finer meshes using the new boundary conditions. In this way, electrostatic fields with different mesh discretization for different regions can be generated.
3.3. EMF and DBF
The electro-motive-force (EMF) is the measurement of the energy needed for a charged particle like ion to cross the ion channel embedded in a membrane. Part of this potential energy barrier is due to the interaction between the crossing ion and the permanent/partial charges on the protein residues. The other part comes from the induced dipoles in the protein/membrane dielectric medium, and is referred as dielectric-boundary-force (DBF). To compute the DBF alone, one may turn off all the static charges on the protein residues and drag the ion through the pore and compute the energy barrier using
- [math]\displaystyle{ P_{DBF} = \int -d \hat{z}. \vec{E} }[/math]
It is important to note that EMF or DBF measurements are just qualitative measurements, as an ion does not necessarily cross the channel through the center of its lumen in a straight line and it is often accompanied by other ions moving in the same or opposite directions, which dramatically changes the dynamics of the system. Moreover, unlike steered MD calculations where the protein residues dynamically reposition themselves as an ion or ions are bouncing across the channel, in our EMF or DBF calculations protein is modeled as a static continuum, which further affects the energy calculations in a more quantitative way. Another issue that additionally impacts the measurements is absence of water hydration molecules, which move with the ion and shield part of its charge. Having said all of above, still computing EMF or DBF is valuable to address channel selectivity or gating. Computing either of these two energy barriers is available as an option in BioMOCA.
3.4. Visualization Using VMD

VMD[14] was equipped with the option of loading BioMOCA structures. This is a very useful feature as one could load both the protein structure (i.e. PDB or PQR file) along with the structures generated by BioMOCA to make comparisons. Figure at the right shows how BioMOCA has generated a structure for Gramicidin channel with a membrane wrapped around it. Furthermore, BioMOCA also dumps the ion trajectories in standard formats so they could be later loaded to molecular visualization tools such as VMD and watched frame by frame in a movie format.
3.5. Recording Trajectories in Binary
Other than counting the number of ions crossing the channel, sometimes it is desirable to study their behavior at different regions of the channel. Such examples would be the average occupancy of ions or their average moving velocity inside the channel or a nanopore. BioMOCA has been equipped with the option of dumping every ions position, average and instantaneous velocities, potential and kinetic energies, average and instantaneous displacements and other info at every step (or few steps) of the simulations in ASCII format, so such trajectory information could be studied later on to gather further statistics. From a technical point of view however, dumping such information for tens of ions, even at every few hundreds of time steps, could slow down the simulations and end up with huge files accumulating to tens of gigabytes. Loading such files later on from disk storage is also a very time-consuming and computationally inefficient procedure. Over and above that, recoding the numerical information in ASCII format does not hold its machine precision and has loss of accuracy.
Solving such problems is actually an easy task and it is simply to avoid using ASCII format and use binary format instead. Not only it preserves the machine accuracy but also writing and reading to file system is a lot faster. The computational overhead to dump the trajectories becomes negligible and the trajectory files become about two orders of magnitude smaller in size. The downside might be that programming and decoding the data could become very tricky, but once it's done correctly and with care, the advantages of using binary format are well worth the extra effort. BioMOCA is now equipped with the tools to record the trajectory information in binary format.
References
- R. Hockney, J. Eastwood, Computer Simulation Using Particles, McGraw-Hill, New York (1981)
- van der Straaten, T.A.; Kathawala, G.; Trellakis, A.; Eisenberg §, R.S.; Ravaioli, U. (2005-02-15). "BioMOCA—a Boltzmann transport Monte Carlo model for ion channel simulation". Molecular Simulation (Informa UK Limited) 31 (2–3): 151–171. doi:10.1080/08927020412331308700. ISSN 0892-7022. https://dx.doi.org/10.1080%2F08927020412331308700
- Toghraee, Reza; Mashl, R. Jay; Lee, Kyu Il; Jakobsson, Eric; Ravaioli, Umberto (2009). "Simulation of charge transport in ion channels and nanopores with anisotropic permittivity". Journal of Computational Electronics (Springer Science and Business Media LLC) 8 (2): 98–109. doi:10.1007/s10825-009-0272-4. ISSN 1569-8025. PMID 20445807. http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=2863032
- Warshel, Arieh; Russell, Stephen T. (1984). "Calculations of electrostatic interactions in biological systems and in solutions". Quarterly Reviews of Biophysics (Cambridge University Press (CUP)) 17 (3): 283–422. doi:10.1017/s0033583500005333. ISSN 0033-5835. PMID 6098916. https://dx.doi.org/10.1017%2Fs0033583500005333
- Schutz, Claudia N.; Warshel, Arieh (2001). "What are the dielectric "constants" of proteins and how to validate electrostatic models?". Proteins: Structure, Function, and Genetics (Wiley) 44 (4): 400–417. doi:10.1002/prot.1106. ISSN 0887-3585. PMID 11484218. https://dx.doi.org/10.1002%2Fprot.1106
- Warshel, Arieh; Papazyan, Arno (1998). "Electrostatic effects in macromolecules: fundamental concepts and practical modeling". Current Opinion in Structural Biology (Elsevier BV) 8 (2): 211–217. doi:10.1016/s0959-440x(98)80041-9. ISSN 0959-440X. PMID 9631295. https://dx.doi.org/10.1016%2Fs0959-440x%2898%2980041-9
- Roux, Benoît; Allen, Toby; Bernèche, Simon; Im, Wonpil (2004). "Theoretical and computational models of biological ion channels". Quarterly Reviews of Biophysics (Cambridge University Press (CUP)) 37 (1): 15–103. doi:10.1017/s0033583504003968. ISSN 0033-5835. PMID 17390604. Bibcode: 2004APS..MAR.J7004R. http://edoc.unibas.ch/1689/1/theoretical_and_computational_models_of_biological_ion_channels.pdf.
- S. Selberherr, Analysis and Simulation of Semiconductor Devices, New York, Springer-Verlag Wien, (1984). ISBN:3-211-81800-6
- Baker, N. A.; Sept, D.; Holst, M. J.; McCammon, J. A. (2001). "The adaptive multilevel finite element solution of the Poisson-Boltzmann equation on massively parallel computers". IBM Journal of Research and Development (IBM) 45 (3.4): 427–438. doi:10.1147/rd.453.0427. ISSN 0018-8646. https://dx.doi.org/10.1147%2Frd.453.0427
- C. Jacoboni, P. Lugli, The Monte Carlo Method for Semiconductor Device Simulation, Springer Verlag, New York (1989)
- Im, Wonpil; Roux, Benoı̂t (2002). "Ion Permeation and Selectivity of OmpF Porin: A Theoretical Study Based on Molecular Dynamics, Brownian Dynamics, and Continuum Electrodiffusion Theory". Journal of Molecular Biology (Elsevier BV) 322 (4): 851–869. doi:10.1016/s0022-2836(02)00778-7. ISSN 0022-2836. PMID 12270719. https://dx.doi.org/10.1016%2Fs0022-2836%2802%2900778-7
- T. A. van der Straaten, J. M. Tang, U. Ravaioli, R. S. Eisenberg and N. Aluru, J. Comp. Elect. 2, 29 (2003)
- Wang, Hai-Long; Toghraee, Reza; Papke, David; Cheng, Xiao-Lin; McCammon, J. Andrew; Ravaioli, Umberto; Sine, Steven M. (2009). "Single-Channel Current Through Nicotinic Receptor Produced by Closure of Binding Site C-Loop". Biophysical Journal (Elsevier BV) 96 (9): 3582–3590. doi:10.1016/j.bpj.2009.02.020. ISSN 0006-3495. PMID 19413963. Bibcode: 2009BpJ....96.3582W. http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=2711404
- "VMD - Visual Molecular Dynamics". http://www.ks.uiuc.edu/Research/vmd/.




