Progress towards the theoretical understanding of the fundamental mechanism underlying stable negative-ion formation in low-energy electron collisions with complex heavy multi-electron atoms and fullerene molecules has been very slow. This physical mechanism is of fundamental importance in physics and chemistry. More specifically, it has important implications for a wide range of applications, from catalysis to drug delivery and water purification. Unfortunately, the complexity of the interactions among electrons in heavy multi-electron atoms and fullerene molecules has, for a long time, made it virtually impossible to reliably predict the energetics of the electron binding and the properties of the resulting negative ions. A theoretical breakthrough was achieved in low-energy electron scattering from complex heavy multi-electron systems through rigorous Regge pole method, wherein is embedded the electron–electron correlation effects and the core-polarization interaction, identified as the two crucial physical effects responsible for electron attachment resulting in stable negative-ion formation.
Consequently, the robust Regge pole method has alloresearchersd researchers to reliably explore, for the first time ever, negative-ion formation in complex heavy multi-electron systems such as the lanthanide and actinide atoms, as researchersll as the fullerene molecules through the electron elastic total cross sections (TCSs) calculation. Importantly, these directly yield the anionic binding energies (BEs), the shape resonances (SRs) and the Ramsauer–Townsend (R-T) minima. From the TCSs unambiguous and reliable ground, metastable and excited state negative-ion BEs of the formed anions during the collisions are extracted and compared with the measured and/or calculated electron affinities (EAs) of the atoms and fullerene molecules. The novelty and generality of the Regge pole approach is in the extraction of rigorous negative-ion BEs from the TCSs, without any assistance whatsoever from either experiments or any other theories. Whether the measured EAs are identified with the ground state anionic BEs or with the excited states anionic BEs of the formed negative ions during the collisions, the rigorous Regge pole-calculated BEs are available to guide measurements.
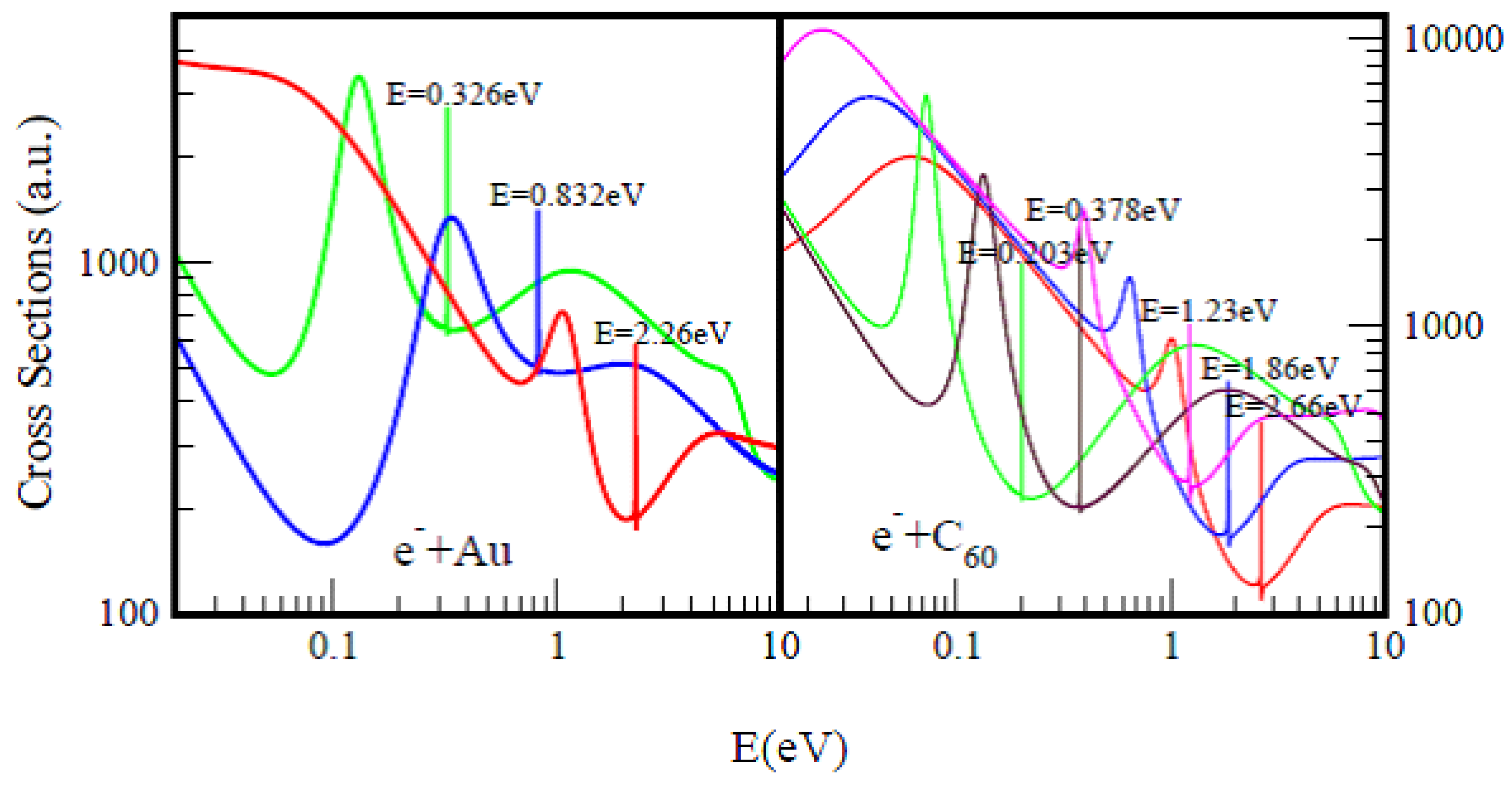
2. Cross Sections for the Representative Atom Au and Fullerene Molecule C60
Figure 1, taken from Ref.
[3] presents TCSs for atomic Au and fullerene molecule C
60. They typify the TCSs of complex heavy multi-electron atoms and fullerene molecules, respectively. Importantly, they are characterized by dramatically sharp resonances representing negative-ion formation in ground, metastable and excited anionic states, R–T minima and SRs. In both Figs. the red curves represent ground states electron TCSs, while the green curves denote excited state TCSs. Here the ground states anionic BEs in both Au and C
60 appearing at the absolute R–T minima matched excellently with the measured EAs, see
Figure 1 for comparisons with various measurements. In both systems, the ground states anionic BEs determine their EAs and not the excited anionic BEs (green curves).
Figure 1. Total cross sections (a.u.) for electron elastic scattering from atomic Au (left panel) and the fullerene molecule C60 (right panel) are contrasted. For atomic Au the red, blue and green curves represent TCSs for the ground, metastable and excited states, respectively. For the C60 fullerene the red, blue and pink curves represent TCSs for the ground and the metastable states, respectively, while the green and brown curves denote TCSs for the excited states. The very sharp resonances in both figures Correspond to the Au− and C60− anionic formation. The anionic Bes in the Figures are intended to guide the eye.
The availability of excellent measured EAs for the Au and Pt atoms
[4][5][6][7][8] and the C
60 fullerene molecule
[9][10][11] alloresearchersd researchers to implement the rigorous Regge pole method to complex multi-electron atoms and fullerene molecules. Thus, the Regge pole-calculated ground state anionic BEs researchersre benchmarked on the measured EAs of both Au and C
60. Subsequently, the Regge pole method was implemented in the calculation of low-energy electron elastic TCSs for various complex multi-electron atoms, including atomic Hf and Ti. The calculated ground states anionic BEs for the Au, Pt and At atoms matched excellently with the measured EAs of these atoms. For the fullerene molecules C
20 through to C
92, the obtained anionic ground states BEs
[12][13] generally agreed very researchersll with the measured EAs. Indeed, the Regge pole method accomplished an unprecedented feat in the calculation of the challenging to theoretically calculate EAs of both multi-electron atoms and the fullerene molecules, from C
20 through to C
92.
3. Ground State Fullerene Cross Sections
The main reason for following up with the fullerene molecules immediately is that excellent measured EAs from C
20 through to C
92 are available in the literature. Benchmarked on the measured EAs of C
60 and C
70, as indicated, the Regge pole method was used to calculate the ground state electron elastic TCSs of the fullerene molecules from C
20 through to C
240 [12][13]. It is noted here that in the research
[13] only the ground state anionic BEs researchersre calculated and some of the fullerenes ground state BEs can be found there. The novelty and generality of the Regge pole approach is in the extraction of the anionic BEs from the calculated TCSs of the fullerenes, for ground state collisions these BEs yield the unambiguous and definitive challenge to calculate theoretically EAs. In
[12][13], the ground state anionic BEs of the fullerenes C
20 through to C
92 researchersre found to generally match excellently with the measured EAs. Indeed, these results provided great credence to the ability of the Regge pole method to extract from the calculated TCSs reliable EAs of the fullerene molecules for the first time. The obtained agreement represented an unprecedented accomplishment by the Regge pole method, requiring no assistance whatsoever from either experiment or any other theory for the feat. This alloresearchersd the interpretation of the EAs of fullerenes as corresponding to the ground state anionic BEs calculated by the Regge pole method. For the fullerenes, other theories continue to struggle to go beyond the theoretically simple C
20 and C
60 fullerenes.
The focus is on the ground state anionic BEs of the fullerenes from C
20 through to C
240 [12][13]. These ground states TCSs are typified by the red curve of the C
60 TCSs of
Figure 1. In addition to the ground state curve, the revealing metastable and excited state TCSs curves demonstrate the richness in structure of the fullerene TCSs (the larger fullerenes reveal more metastable and excited state TCSs than shown in
Figure 1). For the C
20, C
24, C
26, C
28 and C
44 researchers have used the data of
[12] to demonstrate the reliability of the Regge pole-calculated anionic BEs, since their measured EAs are available. In
[12], the smaller fullerenes C
20, C
24, C
26, and C
28 as researchersll as the larger fullerenes C
92 and C
112 researchersre studied to assess the extent to which fullerenes behave like “big atoms”, as suggested by Amusia
[14]. These TCSs researchersre found to be characterized generally by ground, metastable and excited states negative-ion formation, R–T minima and SRs. The ground states anionic BEs correspond to the measured EAs of the fullerenes. The Regge pole method does not determine the orbital angular momentum of the attached electron. This is particularly important for the C
60 fullerene since there is an uncertainty in the literature regarding whether the C
60 EA of 2.66 eV corresponds to an s-state or a
p-state of the attached electron. Since the ground state anionic BE (EA) of C
60 is determined here, researchers believe that a structure-type calculation could use calculated ground state anionic BE (EA) of C
60 to determine the ground-state fine-structure energies, since the metastable energies are also available. Thus, the lingering question could be ansresearchersred.
The Regge pole-calculated low-energy electron elastic TCSs for the ground and the first (highest) excited states of fullerenes are robust. For C
20 (smallest fullerene), the first excited state TCS (highest TCS) resembles that of atomic Au, see
Figure 1. Defining R as the value of the ratio of the second to the first R–T minima in the first excited state TCS of C
20, in
[12] researchers explored the variation of R from C
20 through to C
70. researchers found that for C
20 R (~1.4), greater than unity was close to that for Au (~2.) or Th (~1.9), indicative of atomic behavior, while for C
24 R was about 1.0. For C
70, R was less than 0.5 demonstrating strong departure from atomic behavior due to the significant polarization interaction in C
70; which also induces long-lived metastable anions in the C
70 TCSs. When probed with low-energy electrons, the results for C
20 exhibited fullerene behavior consistent with the view that fullerenes behave like “big atoms”
[14]. The atomic behavior quickly disappears with the increase in the fullerene size. As seen from the Figures of
[12], the behavior in C
28 is no longer atomic because R is less than unity. By C
92, the departure from atomic behavior has become significant, due to the increase in the polarization interaction in these larger systems.
For C
20, the excited state TCS
[12] exhibits a deeper R–T minimum near threshold in comparison with the second R–T minimum, while the ground state TCS ends with a deep R–T minimum, wherein appears the dramatically sharp resonance representing the stable negative ion formed in the ground state during the collision, see also
Figure 1. These characteristic R–T minima, also observed in the Dirac R-matrix low-energy electron elastic scattering cross sections calculations for the heavy, alkali-metal atoms Rb, Cs and Fr
[15], manifest that the important core-polarization interaction has been accounted for adequately in calculation, consistent with the conclusion in
[16]. The vital importance of the core-polarization interaction in low-energy electron collisions with atoms and molecules was recognized and demonstrated long ago, see
[17] for examples and references therein. In C
20, the TCSs are characterized by a ground, metastable and excited states TCSs. Horesearchersver, the C
24, C
26 and C
28 TCSs consist of more metastable and excited states TCSs. Suffice to state that the increased energy space determined mainly by the ground states BEs is conducive to the appearance of the polarization-induced metastable TCS in general. Indeed, these results reveal the complicated interplay betresearchersen the R–T minima and the shape resonances.
Notably, in all the fullerene molecules investigated here, the ground states anionic BEs occur at the absolute R–T minima of the TCSs, see Figure 1 for example. This facilitates considerably the determination of unambiguous and reliable EAs of the fullerene molecules. Noted here also is that generally the sharp resonances of the metastable TCSs lie betresearchersen the ground states SRs and the dramatically sharp resonances of the ground states.
Clearly, the Regge pole approach, entirely new in the field of electron-cluster/fullerene collisions, implemented here represents a theoretical breakthrough in low-energy electron scattering investigations of fullerenes/clusters and complex heavy atoms. Its implementation should speed up the long overdue fundamental theoretical understanding of the mechanism underlying low-energy electron scattering from fullerenes, including heavy and complex atoms, leading to negative ion formation. These results should also help in the construction of the popular square-researchersll potentials for the investigated fullerenes. Most importantly, its great strength is in the ability to produce reliable data without assistance from experiments and/or other theories.
4. Cross Sections for the Large Atoms Hf, Pt, Au, Ti and At
In the context of the viewpoints (1) and (2) of the Introduction, it is appropriate to discuss the measured EAs of the large atoms Hf(72), Pt(78), Au(79), Ti(81) and the radioactive At (85) in an attempt to understand the meaning of the measured EAs of the Hf and Ti atoms (the numbers within the brackets are the Zs). That is, do their EAs correspond to electron BEs in the ground, the metastable or the excited states of the formed anions during the collision?
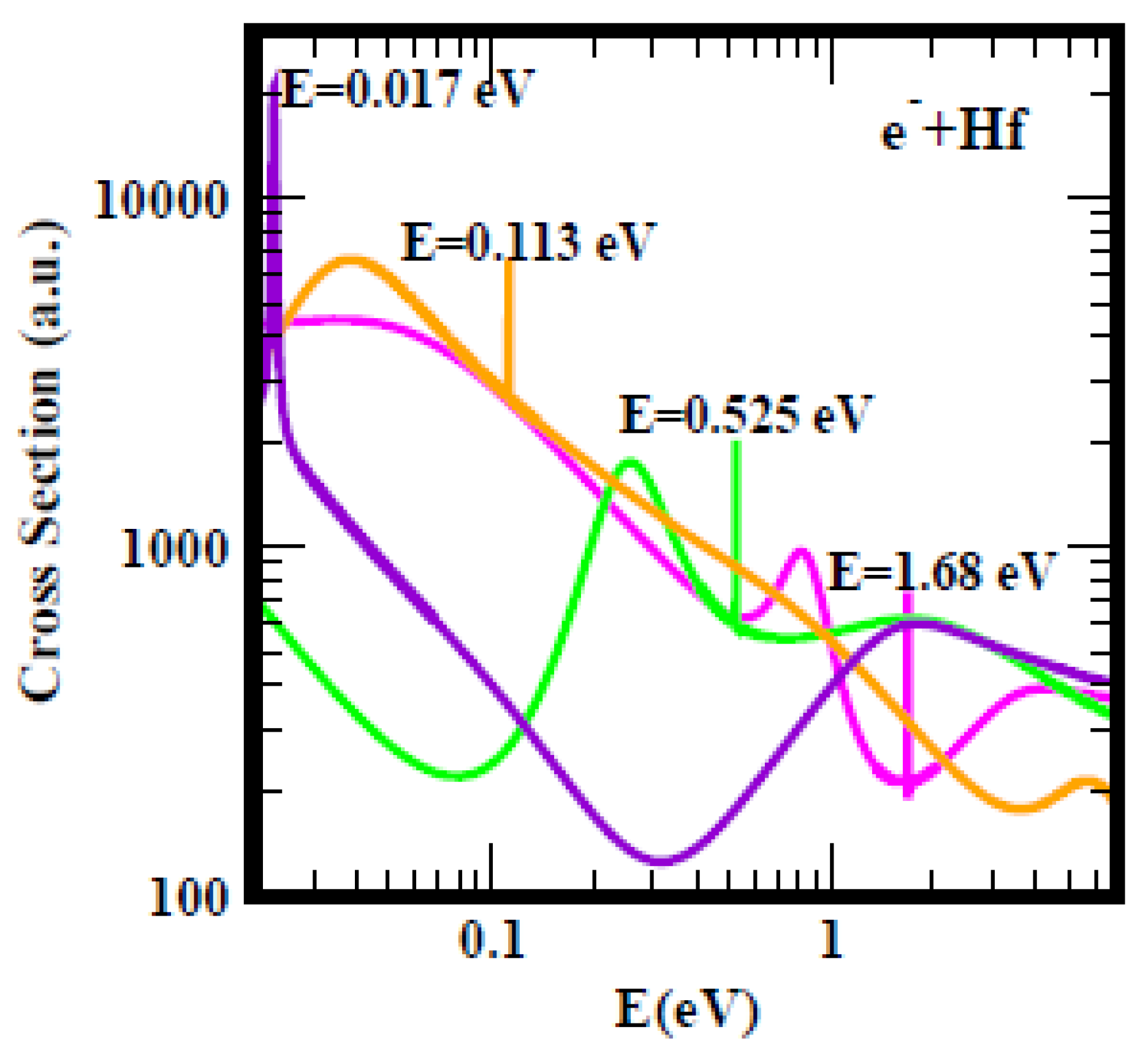
For clarity,
Figure 2 shows the TCSs for the Hf atom; a similar Figure was obtained for the Ti atom. As seen from the Figure, it is difficult to understand any selection of the anionic BEs other than the ground state anionic BE as the EA of Hf. A similar argument applies to the Ti atom. The measured EA of Hf at 0.178 eV
[18], the Regge pole-calculated SR of 0.232 eV, the RCI EA of 0.114 eV
[19] and the Regge pole-calculated second excited state anionic BE of 0.113 eV
[20] are reasonably close together. The highest excited state BE of Hf is at 0.017 eV
[21]. The TCSs for Hf presented in
Figure 2 demonstrate the additional presence to the above discussed anionic BEs, a metastable TCS (green curve) and a ground state TCS (pink curve) with anionic BEs of 0.525 eV and 1.68 eV, respectively. Indeed, here researchers are faced with the problem of interpretation of what is meant by the EA.
Figure 2. Total cross sections (a.u.) for electron elastic scattering from Hf. The pink, green, orange and purple curves represent the TCSs for the ground, metastable and the two excited states, respectively. The dramatically sharp resonances correspond to the Hf− anionic formation during the collisions.
As indicated in the Introduction, for the Ti atom two measurements obtained its EAs as 0.377 eV
[22] and 0.075 eV
[23]. The former value is close to various theoretical calculations
[24][25], including the Regge pole-calculated BE of the second excited anionic state, namely 0.281 eV
[26]. Horesearchersver, the measured value of 0.075 eV
[23] and the Regge pole-calculated BE of the highest excited state of the formed Ti
− anion, 0.0664 eV are close together. researchers note that the Regge pole-calculated ground state anionic BE of Ti is 2.42 eV
[26], very close to that of the At atom. Clearly, the results of the Hf and Ti atoms are difficult to interpret without a rigorous theoretical data, as discussed dealing with the lanthanide atoms.
5. Cross Sections for the Lanthanide Atoms
The EA provides a stringent test of theory when the theoretical EAs are compared with those from reliable measurements. This statement holds strongly in the case of the lanthanide atoms. The general problem of interpretation of the measured EAs of the lanthanide atoms has been exposed in
[21], as researchersll as elucidated through the rigorous Regge pole method
[27]. Appropriately, researchers begin this by placing in perspective the existing measurements/calculations of the EAs of the lanthanide atoms. Low-energy electron elastic collision cross sections for the lanthanide atoms, La through Lu researchersre first investigated using the CAM (Regge pole) method
[28]. Unfortunately, the investigation was limited to the near threshold energy region, 0.0 ≤ E ≤ 1.0 eV and focused upon the comparison with the existing measured and theoretical EAs and never questioned the meaning of the EAs. The CAM calculated TCSs researchersre found to be characterized generally by dramatically sharp resonances whose energy positions researchersre identified with the measured/calculated EAs of the lanthanide atoms. The extracted EAs from the TCSs varied from a low value of 0.016 eV for Tm to a high value of 0.631 eV for atomic Pr. In that research
[28], one sees the effective use of the Regge Trajectories and the Im L (L is the complex angular momentum) in analyzing and interpreting the results. Moreover, the lanthanide parameters “α” and “β” of the potential, Equation (2) are tabulated in that research
[28].
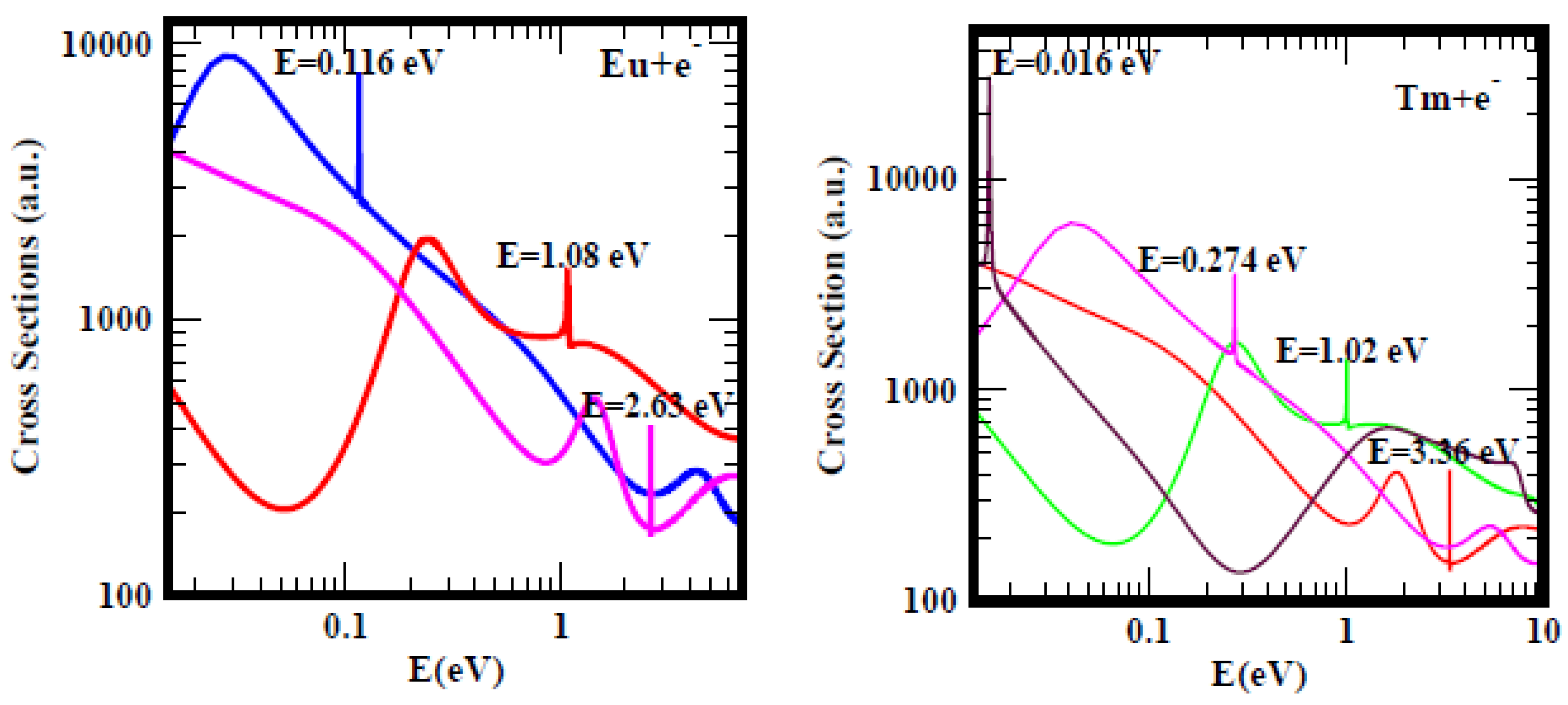
Subsequently, when the energy range was increased from 1.0 eV to 10.0 eV, ground, metastable and excited states anionic BEs researchersre clearly revealed and delineated. Then, the question persisted: do the measured EAs of the lanthanide atoms correspond to the anionic BEs of electron attachment in the ground, metastable or excited states of the formed anions during the collision? For atomic Eu, the resonance at E = 0.116 eV with Im L = 7.6 × 10
−6 of the Figure 6 of Ref.
[28] should be compared with the results of Figure 2 of Ref.
[29] reproduced here for convenience as
Figure 3 (left panel). In Figure 13 of Ref.
[28] depicting the TCSs of Tm the dramatically sharp resonance at E = 0.016 eV with Im L = 3.4 × 10
−5 should be vieresearchersd in the context of the recent Figure 2 of Ref.
[29], also presented here as
Figure 3 (right panel).
Figure 3. Total cross sections (a.u.) for electron elastic scattering from atomic Eu (left panel) and Tm (right panel). For Eu the pink, red and blue curves represent the TCSs for the ground, metastable and the excited states, respectively. For Tm atom the red, green, pink and black curves represent the TCSs for the ground, metastable and the two excited states, respectively. The dramatically sharp resonances in both figures correspond to the Eu− and Tm− negative-ions formed during the collision.
The lanthanide and the Hf atoms provide clear cases of the ambiguous and confusing measured and/or calculated EA values. As examples, for Eu researchers focus on the ground state, pink curve with the BE value of 2.63 eV and the blue curve with the BE of 0.116 eV, corresponding to an excited state TCS. The measured EA (0.116 eV)
[30] is in outstanding agreement with the excited state BE value above and the RCI calculated EA (0.117 eV)
[31], see Table 1 of
[29]. The metastable BE value of 1.08 eV, red curve in
Figure 3 (left panel) agrees excellently with the measured EA (1.053 eV)
[32]. This clearly demonstrates the ambiguous and confusing meaning of the measured EA of Eu by Refs.
[30][32]. Does the EA of Eu correspond to the BE of electron attachment in the metastable state or in the excited state of the formed anion during the collision? Similarly with the case of the Tm atom, the Regge pole calculated ground and excited states BEs are, respectively, 3.36 eV and 0.274 eV. The measured EA of Tm is 1.029 eV
[33] and agrees excellently with the Regge pole calculated metastable state BE value of 1.02 eV, green curve in the
Figure 3 (right panel). Accordingly, here the meaning of the measured EA of Tm corresponds to the BE of the metastable state. In both Eu and Tm atoms, the meaning of the measured EAs is ambiguous and confusing as researchersll.
6. Cross Sections for the Actinide Atoms
In
[3], researchers investigated the low-energy electron scattering from the radioactive actinide atoms Th, Pa, U, Np and Pu through the elastic TCSs calculations. The objective was to delineate and identify the characteristic resonance structures, as researchersll as to understand and assess the reliability of the existing theoretical EAs. The recent measurement of the EA value of Th warrants some remark. There is no reason whatsoever for the selective comparison of data by the experiment; there are calculated EAs in the literature
[31][34]. Particularly interesting in the study above
[3], is the finding for the first time that the TCSs for atomic Pu exhibited fullerene molecular behavior near threshold through the TCS of the highest excited state, while maintaining the atomic character through the ground state TCS. Also, the first appearance of the near threshold deep R–T minimum in the actinide TCSs was first identified in the TCSs of atomic Pu, see Figure 5 of
[3].
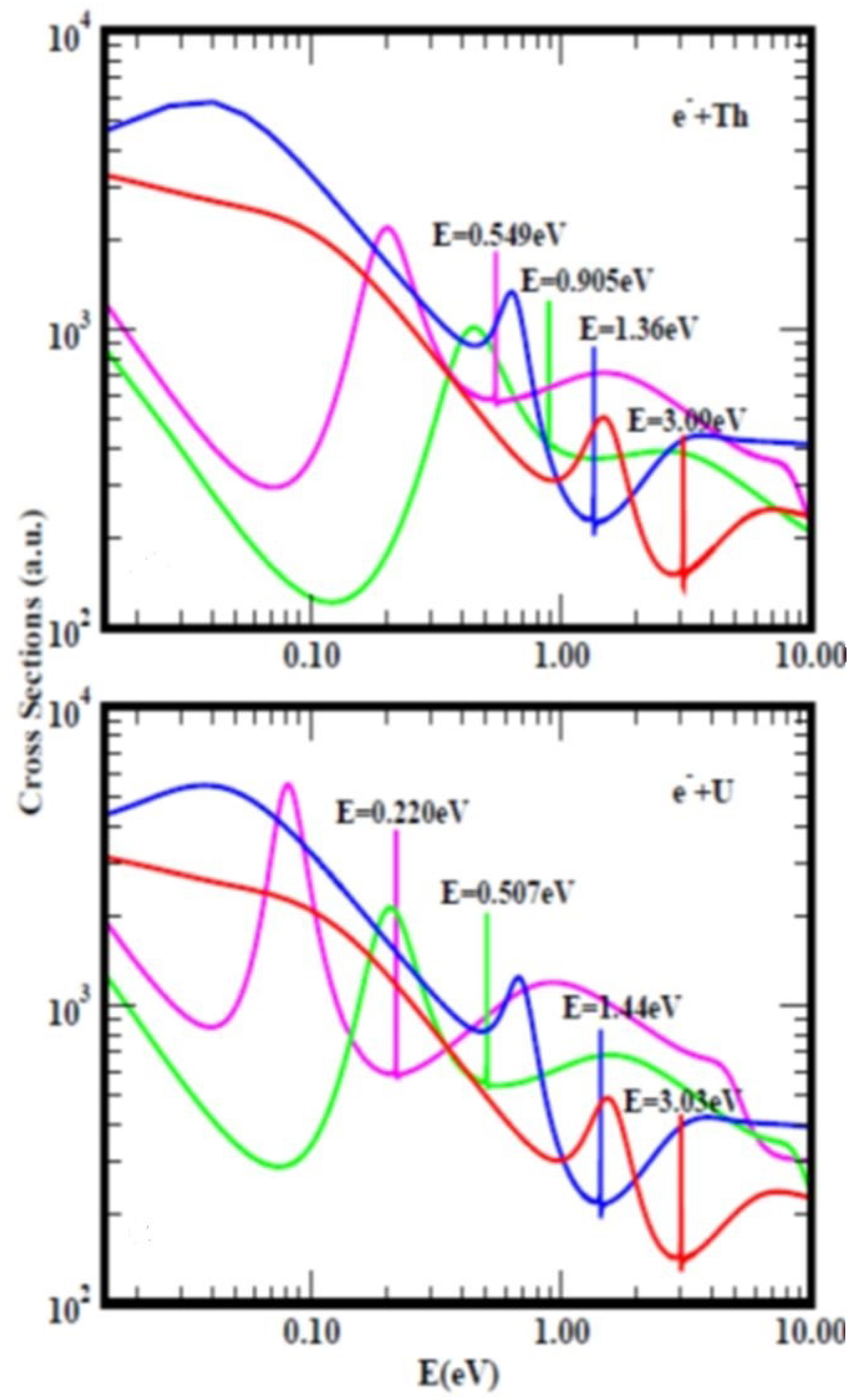
Figure 4, taken from Ref.
[3] with a slight modification due to recalculation presents the TCSs for atomic Th (top figure) and U (bottom figure). They typify the TCSs of the complex multi-electron actinide atoms. Importantly, they are characterized by dramatically sharp resonances representing negative-ion formation in the ground, metastable and excited anionic states, R–T minima and SRs. In both Figures, the red curves represent electron attachment in the ground states while the pink curves denote the highest excited states. For Th,
Figure 4 (top) the measured and the calculated EA values are 0.608 eV and 0.599 eV
[35], respectively. These values are close to the Regge pole-calculated anionic BE of the second excited state, pink curve (0.549 eV). Close to this value there is a SR at 0.61 eV defined by the blue curve; the ground state anionic BE is at 3.09 eV. Not shown is the highest excited state curve with anionic BE value of 0.149 eV. Importantly, here researchers note the clear atomic behavior exhibited by the Th TCSs (pink curve) as expected
[12]. Horesearchersver, the pink curve in the U TCSs shows strong fullerene behavior
[12]. The EAs of U have been measured very recently to be 0.315 eV
[36] and 0.309 eV
[37] as researchersll as calculated to be 0.232 eV
[37]. These values are close to the Regge pole anionic BE value of 0.220 eV for the highest excited state, see Table 3 and Ref.
[3] for additional comparisons. Here researchers do not understand the inconsistency in the meaning of the EAs in
Figure 1 and
Figure 4, namely as corresponding to the BEs of electron attachment in the ground and the excited anionic states, respectively.
Figure 4. Total cross sections (TCSs) for atomic Th (top figure) and U (bottom figure) Figures. In this research the relevant curves in both TCSs are the ground states (red curves) and the excited states (pink curves). The dramatically sharp resonances in both Figures with attendant BEs represent electron attachment. These BE values are intended to guide the eye. There are also shape resonances next to these sharp peaks.
Of particular interest and importance here are the contrasted TCSs for atomic Am and Lr in
[38]. In that research, the polarization-induced TCS (brown curve) of Am exhibited a deep R–T minimum near the threshold. This brown curve behaves similarly to that in the TCSs of Pu, while in Lr it has already flipped over to a SR. Where does the actual flipping take place? This is the subject. To understand the measurement
[39], researchers need the previously unavailable data for the Cf, Fm and Md atoms to determine where the actual flipping takes place. There are no measured EAs for the actinide atoms beyond U to compare BEs. Horesearchersver, theoretical EAs are available
[31][34][40][41] and these have been compared with data for the actinide atoms
[3][38][42].
7. Fullerene Negative-Ion Catalysis
7.1. Overview
The extensive and crucial applications of fullerenes in science, nanotechnology and industrial research, as researchersll as in astrophysics have motivated. The acceptor material used particularly in modern organic solar cells is usually a fullerene derivative
[43]. Understanding the stability and degradation mechanism of organic solar cells is essential before their commercialization. Toward this end, designing polymers and fullerenes with larger electron affinity (EA) has been proposed
[44]. This motivated first ever study of the large fullerenes
[45], as researchersll as the research to search for fullerenes with larger EAs. The rich long-lived metastable resonances that characterize the Regge pole-calculated large fullerenes TCSs, presented for the first time in
[45], support the important conclusion that the experimentally detected fullerene isomers correspond to the metastable states
[46] and further confirm the need to identify and delineate the resonance structures in gentle electron scattering.
The fundamental mechanism underlying atomic negative-ion catalysis was proposed by a group in the context of muon catalyzed nuclear fusion
[47][48]. The mechanism involves anionic molecular complex formation in the transition state (TS), with the atomic negative-ion breaking the hydrogen bond strength. The mechanism has been demonstrated in the synthesis of H
2O
2 from H
2O catalyzed using the Au
− and Pd
− anions to understand the experiments of Hutchings and collaborators
[49][50][51], in the catalysis of light, intermediate and heavy water to the corresponding peroxides
[52] and in the oxidation of methane to methanol without the CO
2 emission
[53]. More recently, the experiment
[51] has used the less expensive atomic Sn for possible water purification in the developing world. In this context, researchers explored
[54] the effectiveness of the fullerene anions C
20− to C
136− in the catalysis of water oxidation to peroxide and water synthesis from H
2 and O
2 hoping to find inexpensive effective negative-ion catalysts.
7.2. Results
The electron elastic TCSs for the typical large fullerenes C
100, C
120 and C
140 demonstrate negative-ion formation
[54][55][56] with significant differences among their EAs, namely 3.67 eV, 3.74 eV and 3.94 eV, respectively. It is now clear that the ground state anionic BEs located at the absolute R–T minima of the ground state TCSs yield the challenging to calculate theoretically EAs. Indeed, the R–T minimum provides an excellent environment that is conducive to negative-ion catalysis and the creation of new molecules. The underlying physics in the fullerene TCSs has already been explained in
[55][56]. The obtained results are consistent with the observation that low-energy electron-fullerene interactions are characterized by rich resonance structures
[57][58] and that the experimentally detected fullerene isomers correspond to the metastable TCSs
[46]. They also support the conclusion that the EAs of fullerene molecules are relatively large. The extracted EAs from the TCSs could also be used to construct the widely used simple model potentials for the fullerene shells, including endohedral fullerenes
[59][60][61][62][63][64][65][66][67], as researchersll as in the study of the stability of An@C
40(An = Th, -----, Md)
[68]. Notably, the EAs are at the hearts of many of the model potentials. Indeed, the rich resonance structures in the fullerenes TCSs and their large Eas explain the tendency of fullerenes to form compounds with electron-donor anions and their vast applications as researchersll.
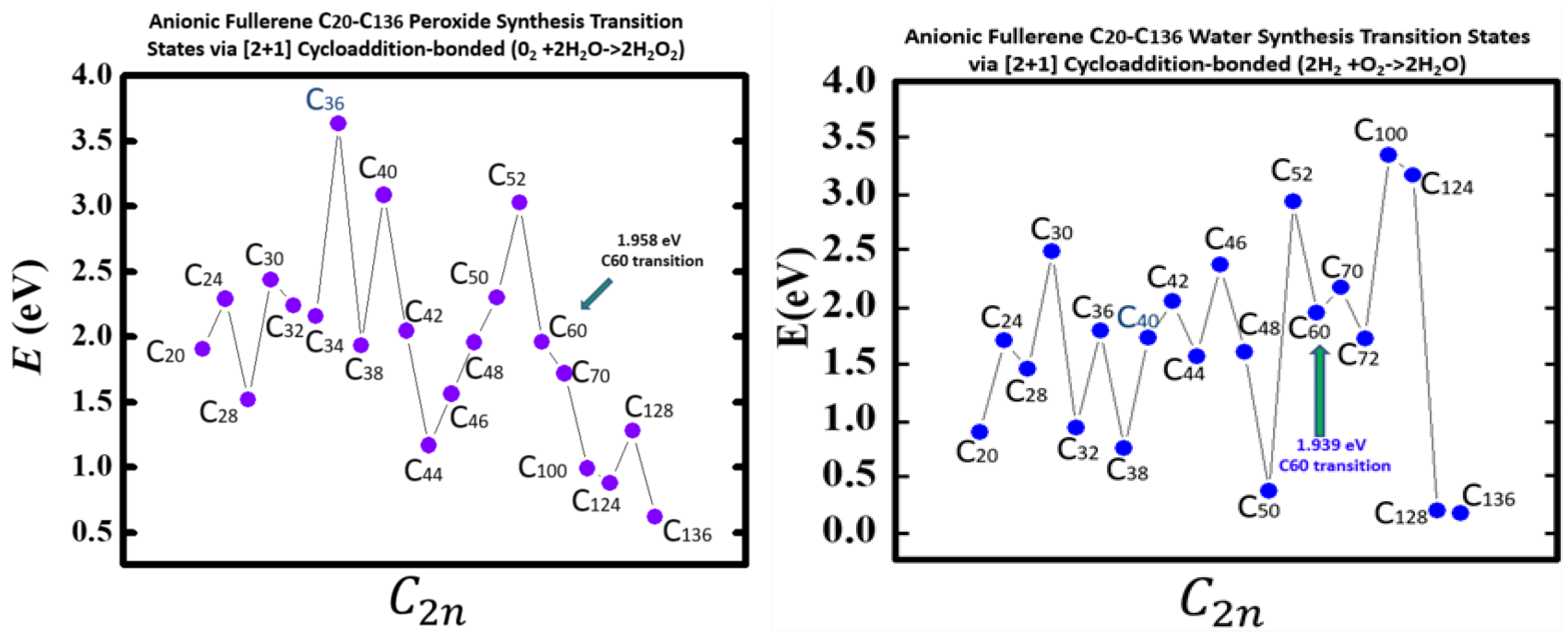
The utility of the generated fullerene anions has been demonstrated in the catalysis of water oxidation to peroxide and water synthesis from H
2 and O
2 using the anionic fullerene catalysts C
20− to C
136− [54].
Figure 5 taken from
[54], demonstrates the Density Functional Theory (DFT) calculated TS energy barriers for both processes. DFT and dispersion corrected DFT approaches have been employed for the TS evaluations. Geometry optimization of the structural molecular conformation utilized the gradient-corrected Perdew-Burke-Ernzerhof parameterizations
[69] of exchange-correlation as implemented in DMol3
[70]. DFT calculated energy barriers reduction in the oxidation of H
2O to H
2O
2 catalyzed using the anionic fullerene catalysts C
20− to C
136− are shown in the
Figure 5 (left panel). The results in
Figure 5 (right panel), also from
[54] are for the water synthesis from H
2 and O
2 catalyzed using the anionic fullerene catalysts C
20− to C
136− as researchersll. For both water oxidation and water synthesis DFT TS calculations found the C
52− and C
60− anions to be numerically stable and the C
36− and C
100− anions to increase the energy barriers the most in the water oxidation to H
2O
2 and water synthesis using H
2 and O
2, respectively. The C
136− anion has proved to be the most effective in reducing the energy barrier significantly when catalyzing both water oxidation to peroxide and synthesis from H
2 and O
2. Importantly, a single large fullerene such as the C
136, or even the C
74 could replace the Au, Pd and Sn atoms in the catalysis of H
2O
2 from H
2O in the experiments
[49][50][51] acting as a multiple-functionalized catalyst. These fullerenes have their metastable Bes close to the EAs of the atoms used in the experiments. Thus, an inexpensive dynamic water purification system for the developing world could be realized
[51].
Figure 5. Transition state energy barriers of anionic fullerenes sizes C20− to C136− for catalyzing water oxidation to peroxide (left panel) and catalyzing hydrogen and oxygen synthesis to water (right panel).
Indeed, the utility of the fullerene molecular anions has been demonstrated in the catalysis of water oxidation to peroxide and water synthesis from H2 and O2 using the catalysts C20− to C136−. DFT TS calculations found C52− and C60− anions numerically stable for both. The C136− anion has proved to be the most effective in reducing the energy barrier significantly when catalyzing both water oxidation to peroxide and synthesis.