Your browser does not fully support modern features. Please upgrade for a smoother experience.

Submitted Successfully!
Thank you for your contribution! You can also upload a video entry or images related to this topic.
For video creation, please contact our Academic Video Service.
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Guofei Qin | -- | 6104 | 2022-06-01 08:05:22 | | | |
| 2 | Conner Chen | Meta information modification | 6104 | 2022-06-01 13:51:28 | | | | |
| 3 | Conner Chen | + 3 word(s) | 6107 | 2022-06-01 13:59:11 | | |
Video Upload Options
We provide professional Academic Video Service to translate complex research into visually appealing presentations. Would you like to try it?
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Qin, G. Configuration Determinations of Flexible Marine Natural Products. Encyclopedia. Available online: https://encyclopedia.pub/entry/23641 (accessed on 11 January 2026).
Qin G. Configuration Determinations of Flexible Marine Natural Products. Encyclopedia. Available at: https://encyclopedia.pub/entry/23641. Accessed January 11, 2026.
Qin, Guofei. "Configuration Determinations of Flexible Marine Natural Products" Encyclopedia, https://encyclopedia.pub/entry/23641 (accessed January 11, 2026).
Qin, G. (2022, June 01). Configuration Determinations of Flexible Marine Natural Products. In Encyclopedia. https://encyclopedia.pub/entry/23641
Qin, Guofei. "Configuration Determinations of Flexible Marine Natural Products." Encyclopedia. Web. 01 June, 2022.
Copy Citation
Flexible marine natural products (MNPs), such as eribulin and bryostatin, play an important role in the development of modern marine drugs. However, due to the multiple chiral centers and geometrical uncertainty of flexible systems, configuration determinations of flexible MNPs face great challenges, which, in turn, have led to obstacles in druggability research. To resolve this issue, the comprehensive use of multiple methods is necessary.
flexible marine natural products
NMR-based methods
circular dichroism-based methods
quantum computational chemistry-based methods
chemical transformation-based methods
1. NMR-Based Methods
1.1. J-Based Configuration Analysis (JBCA)
J-based configurational analysis (JBCA) was first reported by Murata and Yasumoto in 1995 and was further formalized by Murata in 1999 and has now become a reliable and efficient tactic that is an extensively used method for determining the relative configuration of 1,2 and 1,3-methine systems, whose chiral carbons can be substituted by C, O, N, Cl, S, or other groups [1][2][3][4][5][6]. In this method, a set of specific coupling constants (3JH,H, 3JH,C and 2JH,C) that has been divided into three ranges (large (L), medium (M), and small (S), according to their magnitude, Table 1) provides key geometric information (such as dihedral angles) for conformation assignment. Thus, the relative configuration can be determined through assigning the conformation by matching the experimentally measured coupling constants with a priori estimations of all of the possible rotamers.
Table 1. 3JH,H, 3JH,C and 2JH,C values (Hz) in oxygenated acyclic systems.
| 3JH,H | 3JH,C | |2JH,C| | ||||||
|---|---|---|---|---|---|---|---|---|
| None | Mono | Di | None | Mono | Di | Mono | Di | |
| S | 2–4 | 1–4 | 0–3 | 1–3 | 1–3 | 1–3 | 0–2 | 0–2 |
| M | 4–9 | 4–8 | 3–7 | 3–6 | 3–6 | 3–5 | 2–5 | 2–4 |
| L | 9–12 | 8–11 | 7–10 | 6–8 | 6–8 | 5–7 | 5–7 | 4–6 |
A general workflow diagram of the configuration assignment in a 1,2-methine system is presented in Figure 1. First, the values of 3JH,H and 2,3JH,C should be measured. The former can be easily extracted with a 1H-1H NMR experiment, whereas the latter is only able to undergo complex data analysis after heteronuclear correlation experiments, such as 2D hetero half-filtered TOCSY (HETLOC), phase-sensitive HMBC (PS-HMBC), or HSQC-TOCSY [7][8][9][10]. If the value of 3JH,H is judged as S or M, then the threo or erythro configuration can be assigned through fitting the measured values to the a priori estimated magnitude of the coupling constants A-1, A-2, B-1, B-2, A-2/A-3, A-3/A-1, B-2/B-3, or B-3/B-1 in Figure 2. Nevertheless, the same magnitude of coupling constants between A-1/A-2 and B-1/B-2, and the other two exceptions (one is the case of all three staggered conformers coexisting with comparable populations, and the other is the condition of a given rotational conformer deviates more than 15° from a staggered one [3], which are not mentioned in Figure 2) will restrict the application of JBCA. Fortunately, these three situations rarely reside in natural products with multiple substituted acyclic structures [1]. When 3JH,H is shown as typical L, NOE/ROE experiments are indispensable due to the coupling constants having the same magnitude. As long as the proton of C1 relates to the proton of C4, it means that C1 and C4 are in gauche alignment, indicating that the main conformer is A-3 and that it is B-3 otherwise.

Figure 1. Workflow of the conformation and configuration arrangement of a 1,2-methine system.

Figure 2. (A) Configuration arrangement of a 1,2-methine system with one conformation. (B) Conformation and configuration arrangement of a 1,2-methine system with multiple conformations.
In a 1,3-methine system, the entire skeleton is split into two moieties (C2-C3 and C3-C4), and the proton on the methylene (C3) in a higher field is designated as H3, while the other is denoted as H3′. Among the two moieties, there are twelve single dominant conformers (Figure 3) and twelve equilibrating rotamers (Figure 4). Following the flow diagram summarized in Figure 5, all of the conformers belonging to the two moieties can be unequivocally identified and further attributed in the configuration as syn or anti.
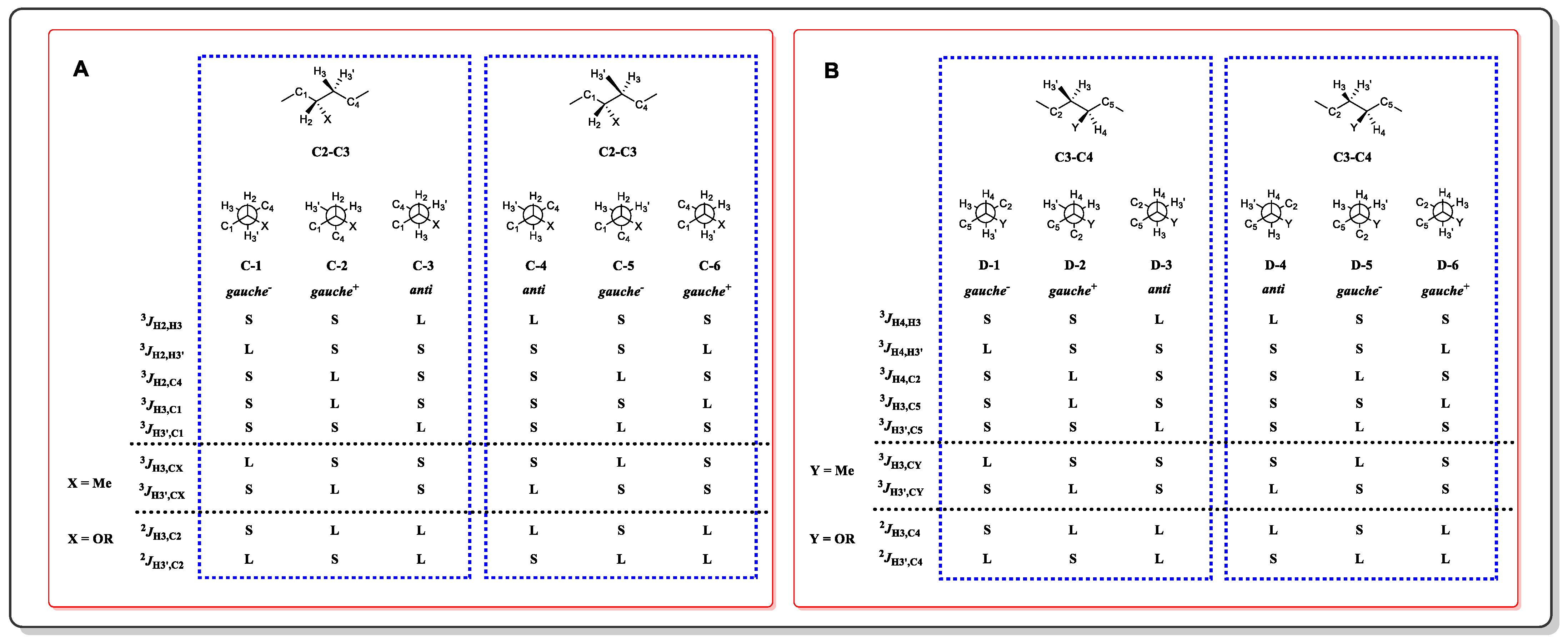
Figure 3. Conformation and configuration analysis of a 1,3-methine system with one dominate rotamer. (A) Configuration arrangement of the C2-C3 moiety. (B) Configuration arrangement of the C3-C4 moiety.

Figure 4. Conformation and configuration analysis of a 1,3-methine system with equilibrating rotamers. (A) Configuration arrangement of the C2-C3 moiety. (B) Configuration arrangement of the C3-C4 moiety.
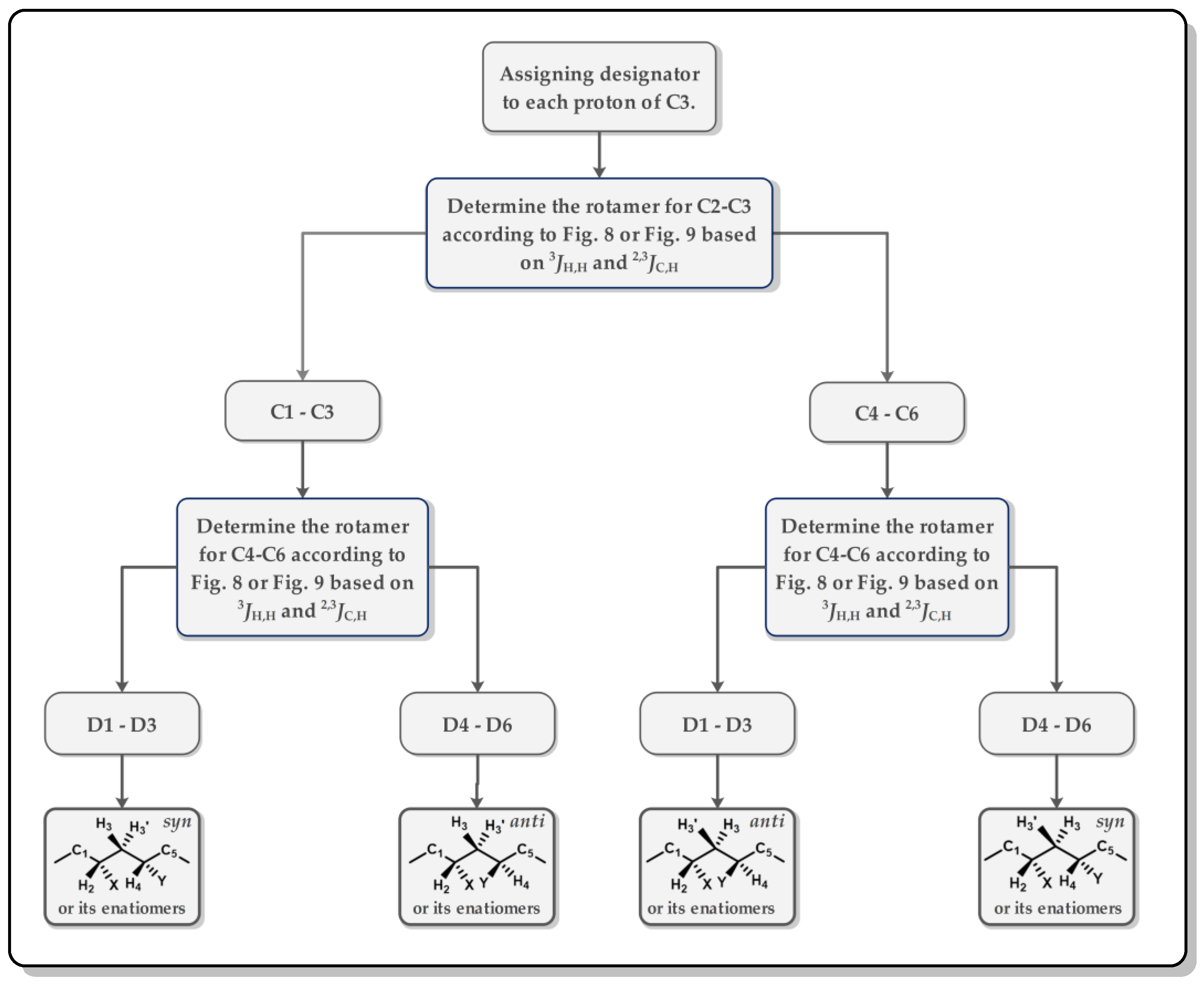
Figure 5. Workflow of the conformation and configuration analysis of a 1,3-methine system.
Ostreol B (5), a cytotoxic and polyhydroxy compound with a long and flexible carbon skeleton, was isolated from cells that were cultivated from the toxic dinoflagellate Ostreopsis cf. ovata collected in South Korea [11]. The configurations of C13–C22 were successfully assigned using the JBCA method. The configuration of C13–C14 was assigned as threo on the basis of 3JH13, H14 = 2.9 Hz, 2JH13, C14 = −1.1 Hz, 3JH13, C14 = 2.0 Hz, and 3JH14, CH3 = 6.2 Hz. As shown in Figure 6, the experimentally obtained coupling data indicated that C15/C18 and H17b/16−OH had an anti orientation, while the coupling constants 3JH17a, H18 = 3.0 Hz, 3JH17b, H18 = 9.2 Hz, 2JH17a, C18 = −1.1 Hz, 2JH17b, and C18 = −5.6 Hz were sufficient to assign an anti relationship between C16/C19 and H-17a/18-OH. Thus, the configuration of C16–C18 was assigned as erythro. C18–C19 was set to a threo configuration on the basis of the four small coupling constants of 3JH18, H19, 2JH18, C19, 2JH19, C18, and 3JH18, C20. For the C19–C21 fragment, the JBCA of C19/C20 and the coupling constants of 3JH20a, H21, 3JH20b, H21, 2JH20a, C21, and 2JH20b, C21 allowed the anti orientation to be assigned to C19/C22 and H20b/21−OH, thereby suggesting a threo configuration between C19 and C21. Thus, the absolute configurations of C13–C22 were assigned as 13R, 14R, 16R, 18S, 19S, and 21S based on the stereochemistry of the 14R and 16R centers, which were assigned through chemical transformation and Mosher’s method. In addition, the configurations within C24–C28 were determined by ROE observation. Moreover, the configuration of C28–C43 was also determined by JBCA, and their main conformations were assigned as shown in Figure 6.
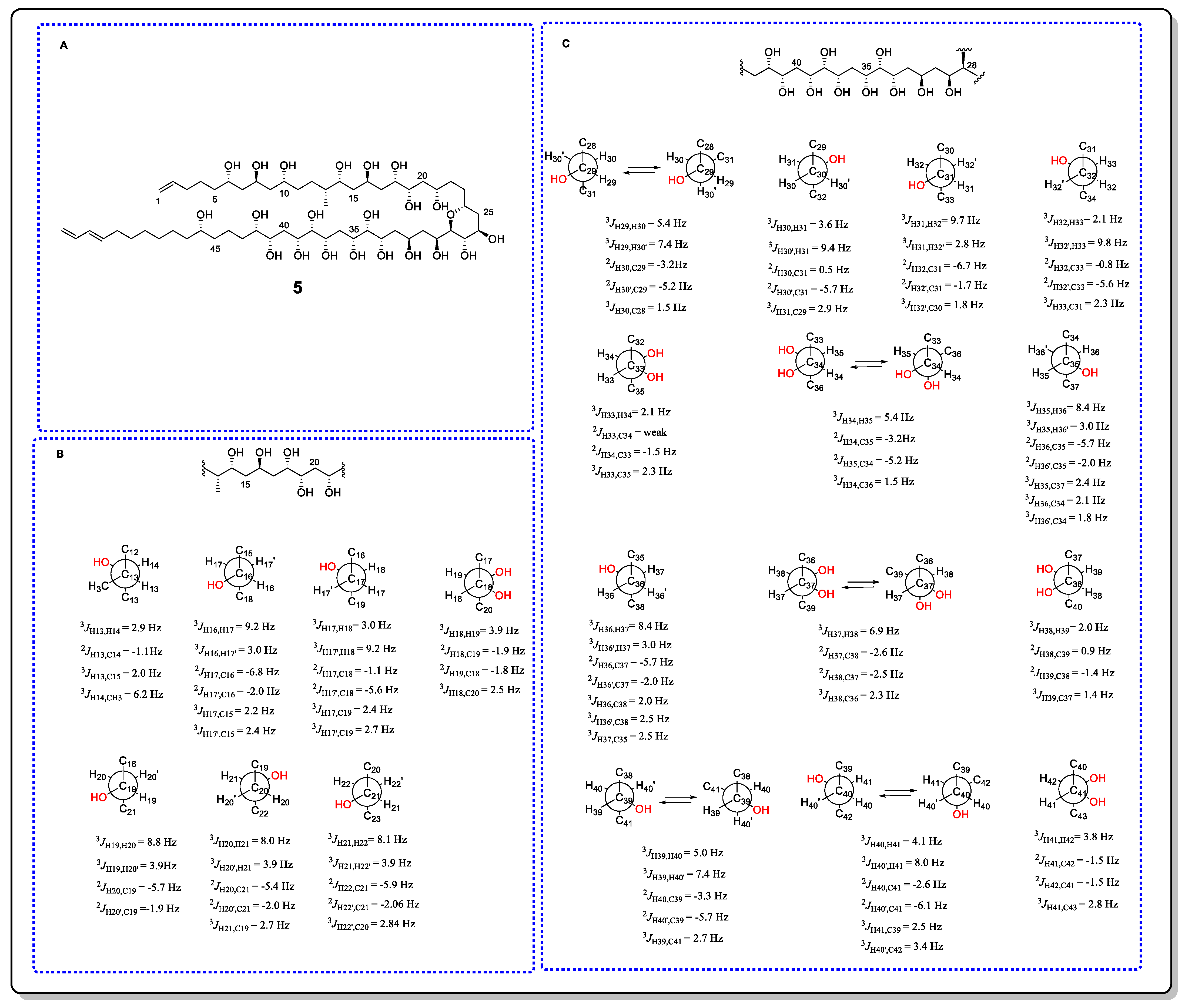
Figure 6. (A) The structure of 5. (B) The JBCA analysis of C13–C22. (C) The JBCA analysis of C28–C43.
1.2. Mosher’s Method
Mosher’s method was first proposed by Professor Mosher in 1973 and has now become a mature and reliable absolute configuration determination method for secondary alcohols due to the improvements that have been made to it over the past few decades [12][13]. Firstly, secondary alcohols react with (R)- and (S)-α-methoxy-α-(trifluoromethyl)phenylacetic acid (MTPA) to generate (R)- and (S)-MTPA esters, respectively [14]. As shown in Figure 7A, the trifluoromethyl group, the carbonyl group of MTPA, and the α-H of secondary alcohol are located in the same plane (Mosher plane, the blue color). Additionally, due to the shielding effect of benzene, the proton chemical shifts of the L2 moiety in (R)-MPTA ester are smaller than those in the (S)-MTPA ester, so the ΔδSR (δ(S)-MTPA ester-δ(R)-MTPA ester) values of L2 should be positive, and the ΔδSR values of the L1 moiety should be negative (in the Mosher ester, determining the absolute configuration of the chiral carbon using the Δδ of βH alone is known as the classical Mosher’s method) [15]. Comprehensively considering the Δδ of the protons of the L1 and L2 moieties is more reliable and is the most commonly used modified Mosher’s method [16]). Then, by calculating the Δδ values of the Mosher esters, the moiety with “−” Δδ values should be placed on the left side of the Mosher plane, and the part with “+” Δδ values should be placed on the right side of the plane (Figure 7B). Finally, IUPAC nomenclature rules are applied to determine the absolute configuration of the secondary alcohols. Shao and colleagues provide a comprehensive standard operating guide for this method [17].

Figure 7. (A) Configurational correlation model and Mosher’s model. (B) Chiral secondary alcohols.
When using the modified Mosher’s method, the positive and negative Δδ values of the Mosher derivatives of the secondary alcohols must be regularly arranged on both sides of the chiral center, and the secondary hydroxyl group with large steric hindrance must be converted to the opposite side [18]. As many Mosher’s agents have been developed [19][20][21][22][23], special attention should be paid to the Δδ (ΔδSR or ΔδRS?) in practical applications. For example, when the -OH groups of (S)-MTPA were replaced with –Cl, the MTPA-Cl with an R absolute configuration was generated (Cahn–Ingold–Prelog (CIP) sequence: -OCH3 > -CF3 > -COOH > -Ph, -OCH3 > -COCl > -CF3 > -Ph); thus, the Δδ of the MTPA-Cl ester should be ΔδRS (δ(R)-MTPA-Cl ester-δ(S)-MTPA-Cl ester) (Figure 7A). In addition, researchers need to be very cautious when using MTPA as a derivatizing reagent because of the very small differences in the chemical shift that are caused by its conformation issues. This means that in some cases, and especially when applied to secondary alcohols, the confidence in the results obtained by the MTPA-based Mosher’s method is not sufficient. In contrast, methoxyphenylacetic acid (MPA), one of the most commonly used ester-forming reagents, has a larger chemical shift difference than MTPA, which leads to it having higher confidence in determining the absolute configuration. Therefore, MPA is clearly superior to MTPA as a derivatizing agent for secondary alcohols [24][25].
Trichophycin C (6), a highly functionalized polyketide possessing a characteristic chlorovinylidene moiety, was isolated from Trichodesmium bloom material collected from the Gulf of Mexico [26]. The absolute configurations at C4 and C10 in its structure were determined using the modified Mosher’s method. The authors used MTPA as the ester-forming reagent to generate the bis-MTPA esters of 6 and calculated the ΔδSR values. As shown in Figure 8, the ΔδSR values are regularly arranged on both sides of the chiral center. Additional “−” Δδ values for H-1, H-2, H-3, H-11, H-13a, H-15, H-19, and H-20 together with “+” Δδ values for H-4, H-5, H-6a, H-6b, H-7, H-8, H-9, H-21, and H-22 revealed absolute configurations of 4S and 10R.

Figure 8. The structure of 6 and the ΔδSR of its MTPA ester.
2. Circular Dichroism (CD)-Based Methods
2.1. Exciton Chirality CD (ECCD)
Exciton chirality CD (ECCD) is a non-empirical and reliable theorizing method that relies on the direct association of the absolute configuration and ECD through the exciton coupling of chromophores (ECD reporter groups) [27][28][29]. It is suitable for chiral systems with two or more non-conjugated chromophores going through electric dipole-permitted transitions [30]. Exciton coupling is initiated by the staggered electric transition dipole moments (TDMs) of two chromophores, which is shown as two Cotton effects with opposite signs in the ECD spectrum. When the positive Cotton effect is localized in the long wavelength range, it indicates that the two TDMs are clockwise from a forward perspective, which is defined as positive chirality (Figure 9). Thus, the relationship of the ECD and stereo-structure information in the molecules is established.
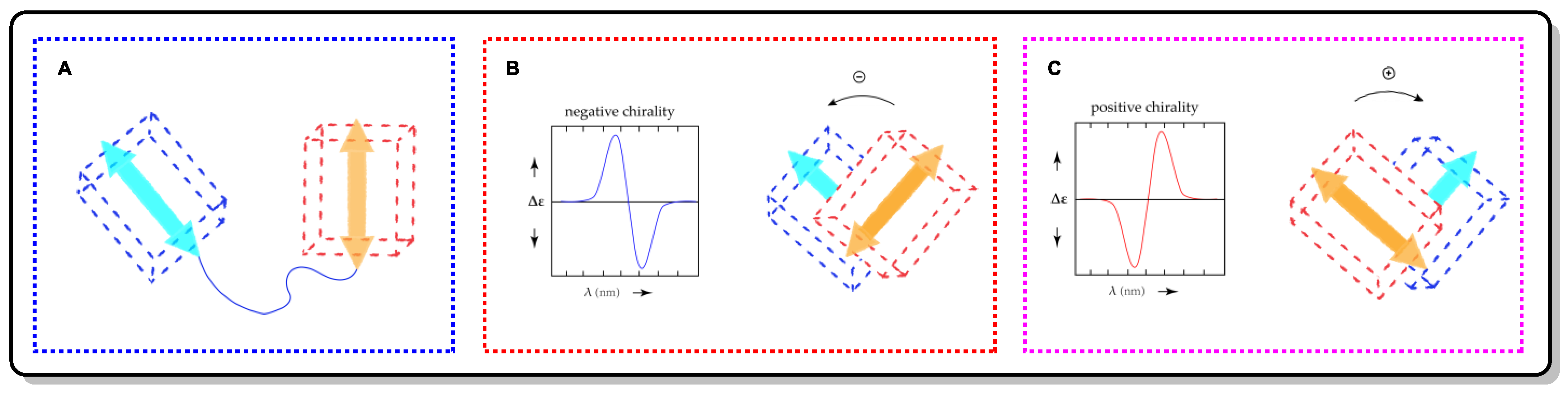
Figure 9. (A) Two chromophores (cubes) and their respective electronic transition dipole moments (arrows). (B) ECD spectrum of negative chirality and its spatial orientation schematic. (C) ECD spectrum of positive chirality and its spatial orientation schematic.
The ECCD analysis workflow follows the following procedures [30]: The first step is to measure the ECD spectra of the molecule with suitable chromophores and to determine the type of exciton coupling (positive chirality or negative chirality). The next step is to determine the dominant conformers of the candidate configurations. Then, the TDM orientation in each chromophore should be assigned accurately. Once the above steps are all completed, the assignment of the configuration can be carried out. As shown in Figure 9, the two TDMs of the chromophores in the dominant conformation of the candidate configuration were placed in front of each other, meaning that their rotation direction (clockwise or counterclockwise) can then be obtained by establishing a sense of rotation to make the front TDM agree with the back one. Thus, the absolute configuration can be assigned by comparing the rotation directions of the TDMs vs. the exciton chirality of the ECD.
ECCD is not as simple as it seems, and it requires careful analysis and extra attention in many respects. Choosing suitable chromophores is the first crucial point to consider before deciding to use ECCD. An eligible chromophore must be capable of electronic π–π* transition. This can be inherent in the molecule or introduced through a chemical reaction. Additionally, the method can still be used when the two chromophores are different. Commonly used chromophoric systems include bis(benzoates), biaryls, benzene derivatives, tetraarylporphyrins (TPP), polyenones, enones, allylic benzoates, and other moieties that are associated with the π–π* component [30]. Benzoic acid-related moieties and TPP are often introduced as chromophores to assist in the determination of molecular configurations. In particular, TPP is suitable for the polyoxygenated polycyclic skeletons of marine natural products that are commonly isolated from dinoflagellates because of its ultra-long-range (40–50 Å) coupling properties [31].
Moreover, the TDM direction within each chromophore should be determined accurately. It is closely related to the symmetry of the chromophore structure. The TDM directions of commonly used chromophores have been studied intensively [32]. However, for some inherent chromophores, the TDM direction is still vague, and their TDM directions should be corroborated by quantum mechanical computations. Besides this, the conformations of candidate molecular configurations also need to be carefully analyzed, and if necessary, a systematic conformational search can be performed to obtain complete conformational information [30].
In addition to what has been mentioned above, the composition of the bonds in the ECD spectrum should also be clarified. The spectrum involves three main aspects: (a) Is the π–π* transition a major contributor to ECD? (b) Is the wavelength region in which exciton coupling occurs truncated by the cutoff wavelength of the solvent? (c) Does electric–magnetic exciton coupling (π–π* transition coupled with n–π* transition) occur?
The absolute configuration assignment of phycotoxin gymnocin B (7) is a classic ECCD application case. Gymnocin B was originally isolated from the dinoflagellate Karenia mikimotoi and possesses a long polyoxygenated polycyclic skeleton with five flexible seven-membered rings [33]. Since the weak reactivity between its secondary hydroxyl groups and MTPA-Cl, the use of Mosher’s method is restricted [34]. Considering the ability of long-range coupling and the low detection threshold of TPP, researchers chose it as the ECD reporter group to settle the charity issue of C10 and C37 (Figure 10). TPP chromophores can be linked to weak reactive hydroxyl groups with relatively high yields using a combined acryloylation/cross-metathesis approach. Additionally, a comprehensive conformational analysis of the simplified TPP derivatives (7b) was performed using molecular mechanic calculations with an MMFF94s force field and Monte Carlo conformational search. Three lowest-energy conformations were obtained, with the Boltzman-weighted populations consisting of 86%, 9%, and 5%, respectively. The interporphyrin twists for the first two conformations were judged as positive, which is consistent with the positive exciton charity that is shown as a positive split Cotton effect (λ (MeOH) 419 nm (Δε +11), 414 nm (Δε −15)) that was observed in the ECD spectra (Figure 10B,C). Thus, the absolute configurations of C10 and C37 were determined to be S and S, respectively.
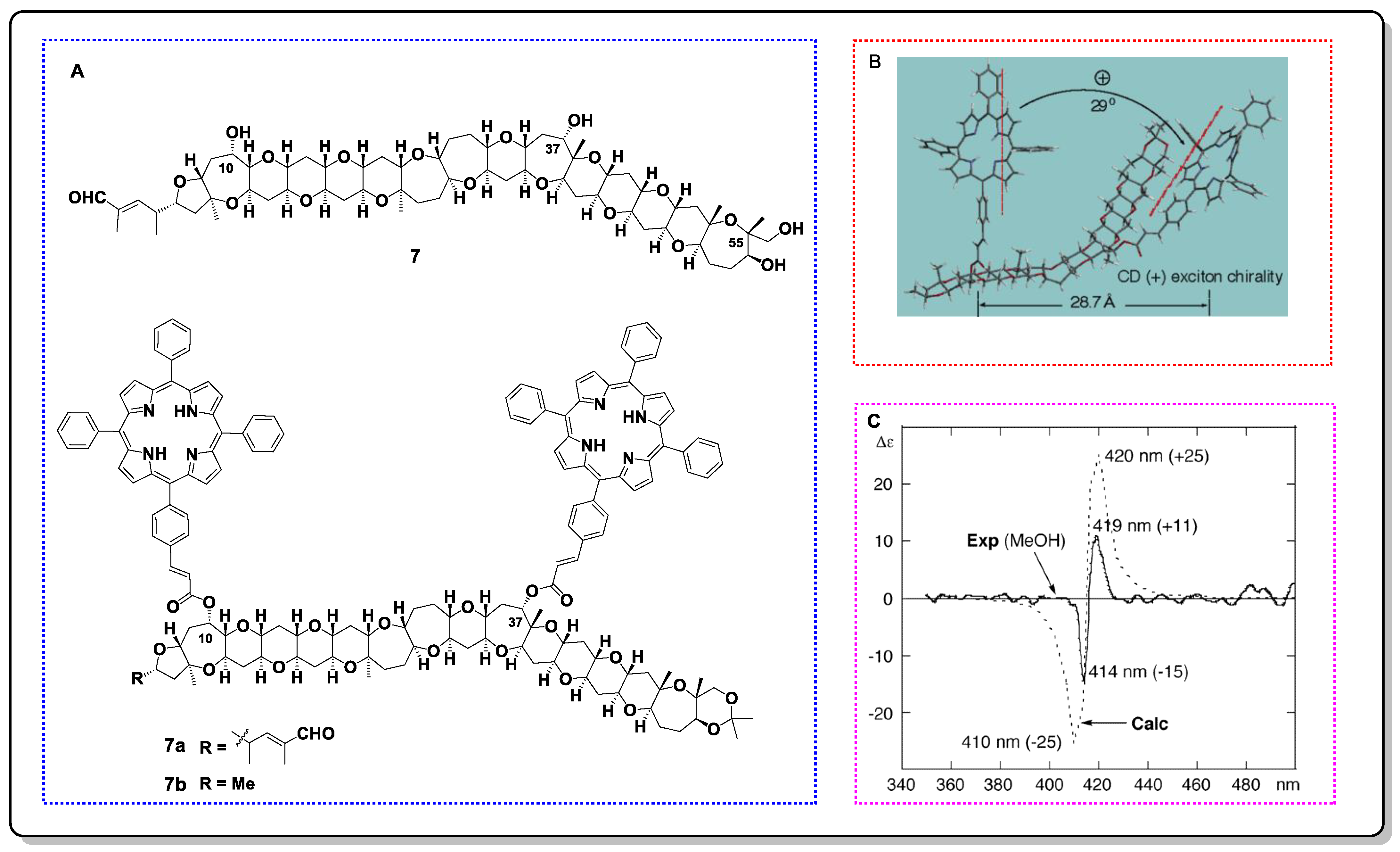
Figure 10. (A) Structure of 7 and its TPP derivative 7a as well as a reasonably simplified derivative 7b. (B) Interporphyrin twist for the main conformation. (C) Experimental and computational maps of ECDs exhibiting positive exciton chirality.
2.2. Complexation-Induced CD (ICD)
2.2.1. Snatzke’s Method (Mo2(OAc)4-Induced CD)
Snatzke’s method, first proposed by Snatzke in 1981, is a convenient and effective empirical approach by which to determine the absolute configuration of cyclic or acyclic 1,2-diols (prim/sec, prim/tert, sec/sec, sec/tert, tert/tert) [35][36]. When mixing vic-diol with a solution comprising an achiral reagent Mo2(OAc)4 (Figure 11A) and during the subsequent measurement of the ICD spectra of the chiral complexes, if the ligating structure had a negative O-C-C-O dihedral (anticlockwise), the Cotton effect at around 310 nm was negative; instead, when it had a positive O-C-C-O torsional angle (clockwise), the Cotton effect at around 310 nm was positive (the helicity rule) [36]. Thus, the absolute configuration of the vic-diols can be determined by the sign of CD at around 310 nm of its Mo2-complex.
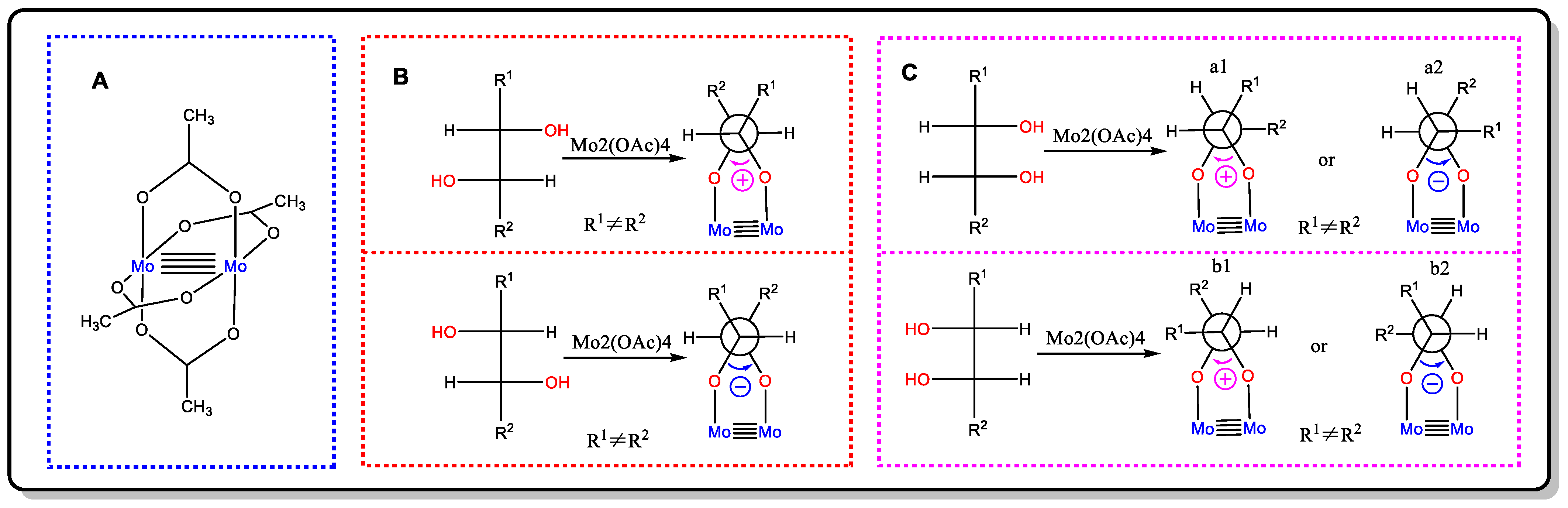
Figure 11. (A) The structure of Mo2(OAc)4. (B) The favorable conformation of the Mo2-complexes of threo-1,2-diols. (C) Two possible arrangements of the Mo2-complexes of erythro-1,2-diols.
Although this method was first proposed to solve the configurational assignment of rigid vic-diols, Górecki’s group and Frelek’s group further developed it to include flexible vicinal diols [36][37]. First, it is necessary to make sure that the relative configuration of the vic-diols is threo or erythro through JBCA, NOE, or a reaction with acetone. If the relative configuration of the vic-diols is threo, then the favorable conformation in the Mo2-complexes of the vic-diols is the one in which both of the O-C-C-R units have an antiperiplanar orientation (Figure 11B). Nonetheless, in the erythro-1,2-diols complexes, there are two possible arrangements for the diol unit, which could lead to the decisive CD having opposite signs for the same absolute configuration (Figure 11C). In this situation, the favorable conformation is that the -R group, which has an O-C-C-R unit with an antiperiplanar orientation, has the biggest steric hindrance. Additionally, if it is difficult to judge which group has the biggest steric hindrance, it is better to refer to the ICD of similar compounds with a known absolute configuration [37].
It should be noted that other functional groups in the 1,2-diols, such as esters, amides, and ethers, do not interfere with the results. However, in the presence of the carboxylic acid group, several hydroxy and/or amino groups would prevent its employment [38]. On the other hand, if there are chromophores in the 1,2-diols, their inherent contributions should be subtracted from the ICD spectra of the chiral complexes.
Bacillcoumacins B (8) and C (9), two amicoumacin-type isocoumarin derivatives, were isolated from the marine-derived bacterium Bacillus sp. [39]. Their side chain contains vic-diol structural fragments. In order to determine the relative configuration of the H-8′ and H-9′ of compound 8, it was conversed to acetonide 8a. The NOE correlations between H-8′ and H-9′ and from both H-8′ and H-9′ to the methyl protons of acetonide depicted an erythro-diol. The erythro configuration of the diol in 9 was assigned by the same JH-8′/H-9′ value of 8 and by the literature. Then, their absolute configurations were determined to be 8′s and 9′S by Mo2(OAc)4-induced CD (Figure 12), respectively. On the basis of the negative Cotton effects at 300 nm, their Mo2-complexes favored the b2 conformation in Figure 11C.
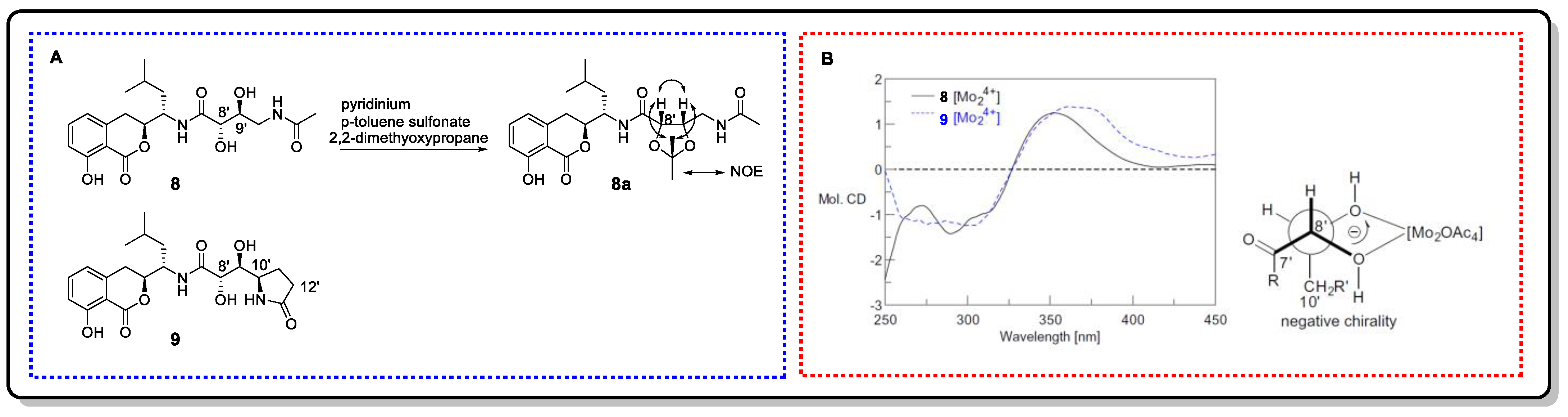
Figure 12. (A) Structures of 8 and 9 and the NOE interactions of 8a. (B) ICD curves of 8 and 9 induced by Mo2(OAc)4 in DMSO-d6.
2.2.2. Rh2(OCOCF3)4-Induced CD
Rh2(OCOCF3)4-induced CD is especially suitable for the absolute configuration determination of secondary and tertiary alcohols. The CD spectra of the Rh2(OCOCF3)4 complexes of chiral alcohols have five Cotton effects (A: 590–585 nm, B: ~500 nm, C: 460–455 nm, D: ~420 nm, and E: ~350 nm) ranging from 270 to 600 nm. The E band can be used to determine the absolute configuration of the secondary or tertiary alcohols by applying the empirical bulkiness rule [40][41]. As shown in Figure 13, when the sign of the Cotton effect for the E band is negative, the structure of the secondary alcohol is of the ‘bR’ type, and when it is positive, the structure of the secondary alcohol is of the ‘bS’ type (according to the size of the substituents, L represents a large substituent and M represents a medium substituent). Thus, the position assignment of each group can be preliminarily determined, and then the absolute configuration of the chiral alcohols can be determined by the CIP system.
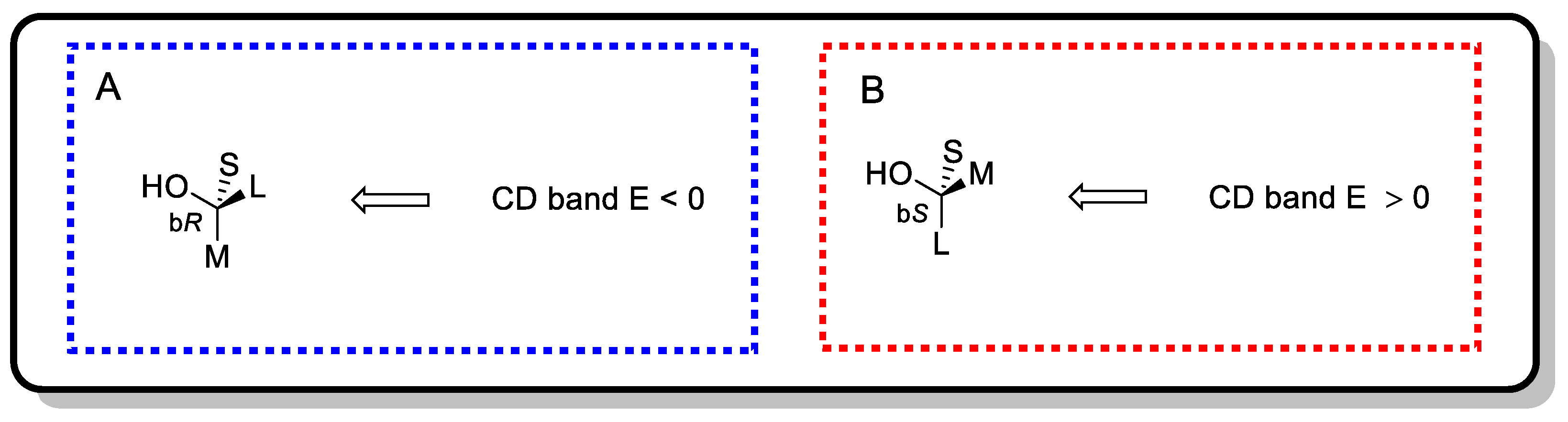
Figure 13. Empirical bulkiness rule for the correlation of the stereoconfiguration of alcohols with the sign of CD band E. (A) bR-configuration. (B) bS-configuration.
If there are multiple functional groups in the alcohols, and especially if the additional functional group is in the vicinity of the chiral hydroxy group, then this method should be applied with caution [41][42]. In this case, the site of complexation and the privileged complexation should be analyzed.
Thalassosamide (10), a new cyclic trihydroxamate compound, is a siderophore discovered from the marine-derived bacterium Thalassospira profundimaris [43]. The 2R, 2′R, and 2″R absolute configuration was established by means of Marfey’s method using fluorodinitrophenyl-5-L-leucine amide (FDLA) as the bifunctional reagent. To elucidate the absolute configuration of C9, C9′, and C9″, rational chemical degradation was performed to obtain three identical diesters, 10a, with original configurations. Then, the absolute configurations of C9 in 10a was deduced as R by the negative E band at 350 nm in the Rh2(OCOCF3)4-induced CD spectrum. Thus, the stereo configuration in the original compound is 9R, 9′R, and 9″R (Figure 14).
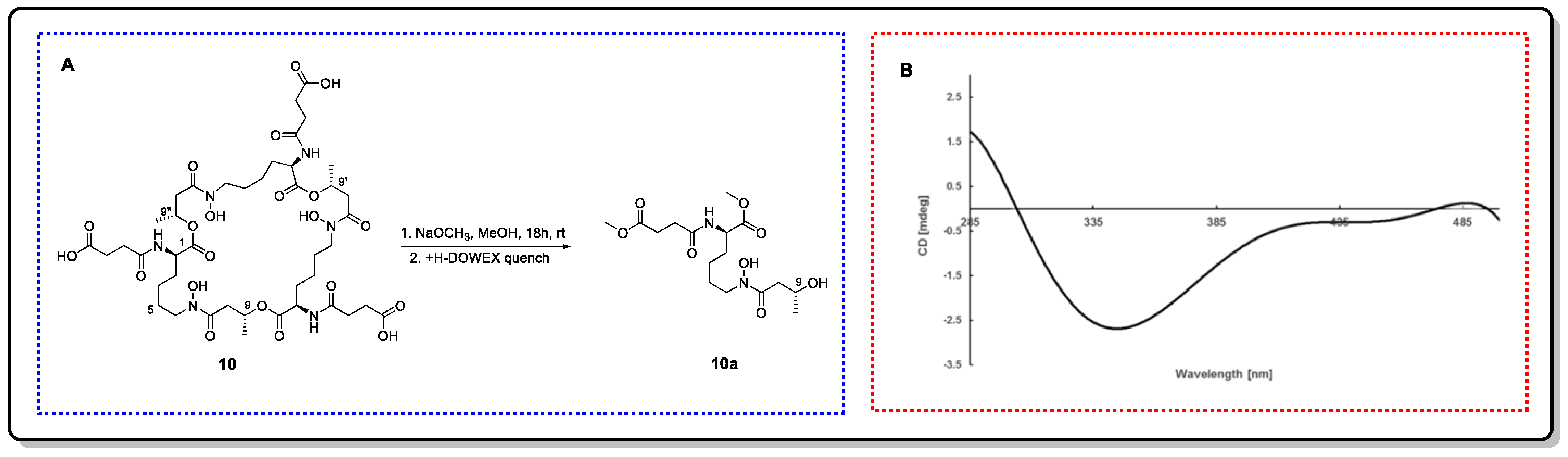
Figure 14. (A) Methanolic fragmentation of 10. (B) ICD curves of 10a induced by Rh2(OCOCF3)4.
Recently, chirality sensing using stereodynamic probes has been successfully applied to determine the absolute configuration of natural products [44][45]. It relies on the strong and characteristic chiroptical readout that is induced by the molecular interactions between a nonracemic chiral substrate and a chromophoric, CD-silent probe. A covalent or non-covalent binding event that conforms to well-defined asymmetry-induced processes can efficiently transfer chiral substrate information (chiral guest) to the stereodynamic sensors (achiral host), thereby leading to a strong Cotton effect in the ultraviolet region of the latter [46]. The molecular configuration can be determined by matching the sign of the Condon effect with the twist direction of a specific structure in the probe. Commonly used probes include bridged biaryls, imine foldamers, trityl propellers, stereodynamic metal complexes, and porphyrins. Among them, the porphyrin-based method is also known as the tweezers method, which can be used to analyze samples with micromolar or sub-micromolar concentrations [47][48]. Additionally, bridged biaryl probes have been applied to natural products, as mentioned at the beginning of the paragraph. Although this method has been proposed and used for many years, to date, there are practically no cases of it being used to determine the absolute configuration of flexible MNPs. However, it performed well when dealing with flexible molecules, and it has the potential to be an interesting approach.
3. Quantum Computational Chemistry-Based Methods
With the continuous progress of related theories and technologies, quantum chemical theoretical calculation methods used to assist in structure identification have become standard methods for confirming the structure of complex natural compounds. By calculating the specific optical rotation (SOR), NMR chemical shift, electronic circular dichroism (ECD), or vibrational circular dichroism (VCD) of a chiral molecule in order to compare it to the measured values, its relative and absolute configurations can be determined.
3.1. NMR Calculations for Marine Natural Products
Following a series of papers on the calculation of NMR parameters for natural products published in the early 2000s by the Bifulco, Köck, Bagno, and Sebag group, a comprehensive paper covering the state-of-the-art in the quantum chemical calculations of NMR parameters in natural product chemistry was published by Tantillo in 2012 [49][50][51][52][53]. Additionally, in more recent years, with the continuous expansion and deepening of related research, the calculation models for determining NMR parameters have experienced significant improvements in terms of their accuracy, reliability, and scope of application, especially in the configurational assignment of natural products [54]. This can be applied not only to determine the molecular configurations but also to the review and correction of previously reported ones [54]. It must be noted that, in general, computational NMR can only determine the relative configuration unless the absolute configuration of a key position has been determined.
Commonly involved NMR parameters for this method are 1H and 13C chemical shifts and spin–spin coupling constants (SSCCs). SSCCs are often used to determine the relative configuration of the local area, while the calculation of the chemical shift of 13C is more widely applied [53]. Besides assisting in carbon signal attribution, SSCCs can also determine the relative configuration of the whole molecule.
The general workflow of NMR calculation includes conformational searches, geometry optimization, the calculation of NMR properties, molecular energy calculations, and Boltzmann averaging, as well as the comparison of the calculated values with those obtained from experiments. It is crucial to choose an appropriate statistical method to evaluate the calculation results in the final step. The statistical methods include classical tactics (e.g., absolute difference, MAE, CMAE, RMSD, and R2) and emerging tactics (e.g., CP3, DP4, DP4+, and J-DP4), by which the correct isomer can be assigned [54][55][56]. The DP4 method, proposed by the Goodman group in 2010, has been the most widely used tool in this field because of its ability to handle problems where only one set of experimental data (1H or 13C chemical shifts) corresponds to multiple candidate structures [57]. It is worth mentioning that there are also two automated versions of this method, PyDP4 and DP4-AI [58][59]. On the basis of this method, Sarotti proposed DP4+ in 2015, which is highly flexible, easy to use, and can handle diverse chemical structures and isomerizations [60]. In addition, J-DP4 incorporates coupling constants into the DP4 analysis, with three modes: dJ-Dp4, IJ-DP4, and iJ/dJ-DP4 [61]. The performance of this strategy is 2.5 times better than the original DP4 method [61].
Due to the complexity and diversity of the conformational isomers of flexible molecules, when performing NMR calculations, the conformational set of each isomer that is randomly generated by the program can be used to replace the calculated conformational distribution, and their DP4/DP4+ probability can then be calculated. This step should be repeated a specified number of times, and the average can be taken to determine the final probability of each isomer [62]. In addition, Hehre and co-workers describe an efficient method for calculating the 13C NMR chemical shifts of flexible natural products that has been tested with numerous cases [63].
In the above section discussing Mosher’s method, the determination of the C4 and C10 chiral center configurations of trichophycin C (6) was discussed as a typical case [26]. The configurations of its other two chiral centers (C5 and C7) were assigned by comparing experimentally obtained SSCCs with theoretically calculated values. To better explain the flexibility of the molecule, geometry optimization was performed at two different functionals (B3LYP and M062X). As clearly shown in Table 2, the RMSD between the theoretically calculated and experimentally measured J-couplings is the lowest for C7RC5R. The “error bars” on the theoretical values were also estimated through comparing the average coupling constants obtained from the conformational distributions that were calculated at the two different functionals and received positive feedback. These results highlight C7RC5R as the stereoisomer for 6, and good agreement is also shown in Figure 15 when combined with 10R and 4S.

Figure 15. (A) Four chiral centers of 6. (B) R2 values for correlations between theoretical and experimental J-couplings for stereoconfigurations at C4, C5, C7, and C10. (C) Plots of theoretical vs. experimental J-coupling values for C7R and C5R at the two different functionals for 6.
Table 2. Comparison of experimentally measured J-couplings with theoretically calculated values for 6.
| Coupling | B3LYP/6-311+g(d,p)//B3LYP/6-31g(d,p) | B3LYP/6-311+g(d,p)//MO62X/6-31g(d,p) | Exp (Hz) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| C7SC5S | C7SC5R | C7RC5S | C7RC5R | C7SC5S | C7SC5R | C7RC5S | C7RC5R | ||
| H6a–C8 | 2.4 | 2.4 | 7.1 | 6.1 | 1.8 | 1.8 | 8.2 | 6.0 | 5.8 |
| H6b–C21 | 3.1 | 3 | 3.8 | 4.3 | 2.7 | 2.5 | 3.1 | 4.7 | 4.0 |
| H6b–C22 | 2.7 | 6.1 | 2.6 | 6.3 | 2.5 | 6.7 | 1.4 | 5.9 | 6.2 |
| H6a–H5 | 8.4 | 9.1 | 11.2 | 9.2 | 10.0 | 10.1 | 11.8 | 8.5 | 9.4 |
| H6b–C8 | 5.1 | 5.1 | 2.2 | 3.1 | 3.7 | 4.6 | 2.1 | 3.2 | 3.8 |
| H6a–H7 | 7.5 | 7.6 | 5.4 | 6.6 | 5.9 | 7.1 | 4.6 | 6.6 | 5.5 |
| H6b–H7 | 8.0 | 8.4 | 10.9 | 9.1 | 10.3 | 9.8 | 12.5 | 9.4 | 9.0 |
| H5–H4 | 4.5 | 3.6 | 3.0 | 4.9 | 4.2 | 3.6 | 3.2 | 6.3 | 5.3 |
| H5–C3 | 2 | 3.6 | 1.5 | 3.3 | 1.8 | 2.9 | 1.2 | 2.7 | 4.1 |
| H4−C6 | 2.1 | 2.9 | 2.1 | 2.8 | 1.9 | 3.4 | 2.0 | 4.0 | 2.7 |
| H4−C22 | 4.6 | 4.3 | 5.3 | 3.7 | 4.8 | 3.9 | 5.5 | 2.9 | 3.5 |
| H5−C4 | 1.4 a | 2.8 a | 0.2 | 3.5 a | 0.8 a | 1.8 a | 0.3 | 3.6 a | 4.7 |
| RMSD (Hz) | 2.1 | 1.6 | 2.2 | 0.7 | 2.2 | 1.8 | 2.7 | 0.9 | |
a The actual calculated value is negative.
In addition to calculating the three classical NMR parameters mentioned above, interproton distances, residual dipolar couplings (RDCs), and residual chemical shift anisotropies (RSCAs) can also serve as calculations. In several candidate structures, the computational predictions of the interproton distances can be complementarily applied to the NOE/ROE information, facilitating accurate and reliable configuration assignments. RDCs and RSCAs are anisotropic NMR parameters that provide angular data about carbon–hydrogen bonds and shielding tensors, respectively. In order to observe RDCs and RCSAs, the molecules must be partially aligned, usually with the help of an orienting media such as confined polymer gels or liquid crystals. For rigid natural product molecules, these two methods can solve configuration issues based on simple calculated models. However, for flexible molecules, simple models are often ineffective. Fortunately, this has been solved to some extent by using RDCs as constraints. Progressive stereo locking (PSL), an RDC-based force field method proposed in 2017, can effectively solve the relative configuration problems of flexible molecules [64]. Luy and colleagues established a method based on time-averaged molecular dynamics with dipole coupling as a tensor orientation constraint, and this method can be used to solve molecular structure problems of any size [65]. More recently, a method called floating chirality restrained distance geometry (fc-rDG) calculations was used to directly evolve structures from NMR data such as NOE or RDCs [66]. In contrast to RDCs, RCSAs have been rarely used, mainly due to the practical difficulty of extracting RCSA from the spectra, as dissolving the analyte in the orienting media introduces both isotropic and anisotropic chemical shift changes [67][68][69][70][71].
3.2. ECD Calculations for Marine Natural Products
some reliable and well-established semi-empirical methods based on ECD spectroscopy used to determine the absolute configuration of chiral molecules, witch are discussed in the above section. Additionally, in recent years, increasing attention has been drawn to addressing the configuration issues resulting from using TDDFT (time-dependent density functional theory) for ECD computation. It is even possible to state that this method has become a standard tactic in the study of natural products. Having a high intuitive ability and clarity is a hallmark of this method. The absolute configuration can be assigned by directly comparing the computationally predicted ECD spectrum with the experimental one.
The typical process for calculating ECD follows several steps. The first step is to perform a conformational analysis on the tested molecule. The dominant conformation that contributes more to the calculation of the ECD spectrum is selected by performing corresponding calculations with appropriate functionals and basis sets that have been selected according to the molecular weight and properties of the molecule. Following this, TDDFT-ECD calculations can be performed on each dominant conformation to obtain a spectrum, and a Boltzmann-weighted average of all of the obtained spectra is then calculated to generate the predicted ECD spectrum of the assumed target configuration. Finally, the absolute configuration of the molecule can be determined by comparing the generated ECD spectrum with the experimental one [28][72][73][74].
Molecules with flexible skeletons usually possess multiple conformations in solution, and their experimental ECD spectra represent the average of those multiple conformations in time and space. Therefore, it is crucial to conduct rational conformational analysis for this class of molecules. The complex conformational distribution of flexible molecules means a significant increase in computational costs and time. In general, natural products from the ocean feature greater flexibility and a higher molecular weight, leading to a longer computation time or a higher probability of errors in the computations. Consequently, it is necessary to combine other methods for comprehensive analysis when necessary.
Fiscpropionates A (12) and B (13), two polypropionate derivatives featuring an unusually long hydrophobic chain, were isolated from the deep-sea-derived fungus Aspergillus fischeri FS452 [75]. The authors determined their relative configurations using a combination of NOESY and coupling constants. Then, the absolute configurations of 12 and 13 were established as 9R, 10R, 12S, 14S, and 16S and 9R, 10R, 12S, and 14S, 16S via quantum chemical calculations of the ECD spectra at the B3LYP/6-311+G(d,p) level (Figure 16).

Figure 16. (A) Structures of 12 and 13. (B) Experimental and theoretical CD spectrums of 12 and 13, respectively.
3.3. VCD Calculations for Marine Natural Products
For natural products whose chromophore is far away from the chiral center or does not contain a chromophore, the corresponding Cotton effect on the ECD spectrum is extremely weak or even non-existent, so it is difficult to use semi-empirical ECD methods or ECD calculations to determine the absolute configuration. Since molecular vibrations are universal, all chiral natural products theoretically feature unique VCD spectra, and the VCD spectrum is better able to reveal subtle conformational and stereochemical differences, so VCD-based methods can be used to settle the absolute configuration of chiral molecules. Nevertheless, the effective and direct interpretation of VCD spectra is very difficult due to the complexity of the molecular vibrational modes. At present, the most effective and reliable method is to compare the calculated VCD spectra of different isomers with the measured spectra to determine the absolute configuration of the chiral compounds [28].
While ordinary DFT methods, rather than the more complex TDDFT, can be applied to calculate VCD spectra, the computation cost remains huge for flexible-skeleton molecules [28][76]. Additionally, the higher accuracy will also inevitably lead to an increase in the calculation time. In addition, the acquisition of the VCD experimental spectrum relies on a relatively high sample concentration (20–50 mg/mL) and a long measurement time (several hours) because of the weak intensity of the VCD band [28][77]. Therefore, it is difficult for this method to be widely used in the determination of the absolute configuration of natural products with limited quantities.
Hemicalide (14), a mitotic inhibitor with high antiproliferative potency against human cancer cell lines at subnanomolar concentrations, was isolated from the marine sponge Hemimycale sp. Collected in the deep water around the Torres Islands (Vanuatu) [78], it features a 46-carbon atom skeleton containing 21 stereocenters. Degradation and derivatization cannot be performed on its trace amount (ca. 1 mg). Relative configurations of C8-C13 and C18-C24 were reasonably assigned by means of comparison with the data obtained from synthesized diastereomeric model compounds and further NMR analysis and calculations [79][80]. In addition, combining stereocontrolled synthesis with NMR, IR, and VCD analyses, the relative configuration of C36-C46 was determined (Figure 17). Specifically, the configuration of C42 was settled by comparing the computational (14a and 14b) and experimental (sample I and II) spectra of VCD after the relative configurations of other chiral centers had been assigned. As shown in Figure 17, the IR of the two candidate isomers (14a and 14b) was evaluated, and no specific differences were found, while the VCD was sufficiently characteristic at 1070–1170 and 1350–1400 cm−1. Good agreement is shown in Figure 17C, and this agreement allows for the unambiguous assignment of II to 14b and I to 14a. According to the NMR match between the prototype molecule of I and 14, the relative configuration of C42 was assigned as shown in the structure of 14a.

Figure 17. (A) Structure of 14 and stereocontrolled synthetic derivatives. (B) Calculated (top) and observed (bottom) IR spectra of 14 a/14 b and samples I/II. (C) Calculated (top) and observed (bottom) VCD spectra of 14 a/14 b and samples I/II.
4. Chemical Transformation-Based Methods
Chemical transformation, or, more specifically, the synthesis and degradation of the molecule, has always been an indispensable method in elucidating the structures of natural products, especially when identifying the configuration of marine natural products, which often contain structural features such as long aliphatic chains and abundant functional groups. Although this method cannot directly determine the configuration of the molecule, it can provide an essential prerequisite for other strategies.
Needless to say, the most ideal solution would be to synthesize various isomers of the tested molecule to compare spectroscopic data. Of course, researchers may synthesize the corresponding configuration after a few years of painstaking effort, but this intellectually difficult and physically tedious approach is not ideal. From a practical standpoint, for difficult-to-synthesize compounds, the best option is to synthesize decisive segments for comparison. For example, amphidinol 3 (AM3) (15) is a marine natural product that is produced by the dinoflagellate Amphidinium klebsii [81]. Subsequently, in 1999, the absolute configuration was determined by extensive NMR analysis and degradation [82] (Figure 18). Recently, the absolute configuration of C2 and C51 has been revised. Tohru and co-workers chemically synthesized the C31-C67 part of 15 and ultimately identified the absolute configuration of AM3 as 32S, 33R, 34S, 35S, 36S, and 38S by combining the degradation of the original compound [83].
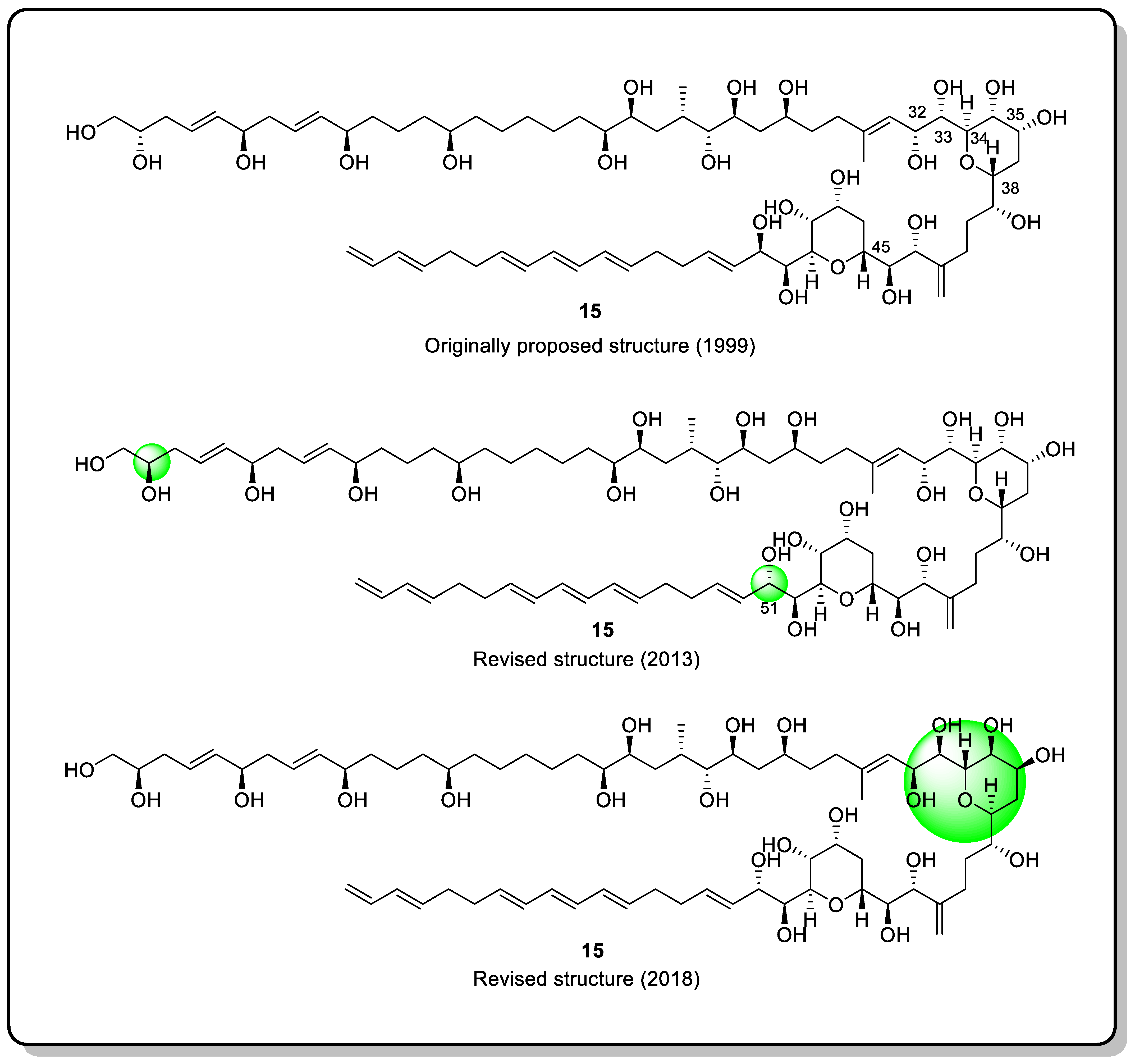
Figure 18. Structure of 15 and the course of its configuration attribution.
The other option is the appropriate degradation or derivatization of new natural products, followed by spectroscopic analysis to tackle their absolute configuration. The attractive reaction involves acetylation, catalytic hydrogenation, hydrolysis, Baeyer–Villiger oxidation, ozonolysis, periodate oxidation, hydrogenolysis, and other oxidative or reductive chemical reactions [84]. After chemical transformations, the determination of complex molecular configurations becomes relatively straightforward. In this area, since there are a number of excellent reviews that already exist, only how Baeyer−Villiger oxidation, ozonolysis, and periodate oxidation may be useful in the context of the structural analysis of natural substrates will be discussed in here.
A classic example is in the work directed toward ascolactone A (16), which was originally isolated from the marine-derived fungus Ascochyta salicorniae. The absolute configuration at C9 was determined by Baeyer–Villiger oxidation with MCPBA followed by the hydrolysis of ester 16a to 16b and 16c [85]. As a result, the configuration of 16c was obtained as R by chiral-phase GC/MS analysis. Combined with NMR analysis data, the configuration of 16 was determined to be 1R, 9R (Scheme 1A).

Scheme 1. (A) Application of Baeyer−Villiger oxidation in the determination of the absolute configuration of 16. (B) Application of oxidative degradation in the determination of the absolute configuration of 17. (C) Application of periodate oxidation in the determination of the absolute configuration of 18.
Ozonolysis was employed to deal with cytotoxic macrolide amphidinolide J (17), which was isolated from the cultured dinoflagellate Amphidinium, a symbiont of the Okinawan Amphiscolops sp. marine flatworm [86] (Scheme 1B). The ozonolysis of 17 followed by NaBH4 reduction and acetylation yielded peracetates, corresponding to its C1–C7, C8–C11, and C12–C16 fragments (17a–17c). The absolute configurations of all six stereocenters were determined by comparing NMR, the MS spectra, and the optical rotation symbols of both the synthesized and fragmentary compounds based on 17.
Periodate oxidation was applied to the structural analysis of phosphoeleganin (18), a novel phosphorylated polyketide from ascidian Sidnyum elegans. To establish two corresponding fragments, 18a and 18b, the compound was oxidatively cleaved with NaIO4 followed by NaBH4. Additionally, the fragments were then subsequently derivatized to Mosher esters. Ultimately, as a result of these conversions, the absolute configuration of 18 was confirmed [87] (Scheme 1C).
References
- Matsumori, N.; Kaneno, D.; Murata, M.; Nakamura, H.; Tachibana, K. Stereochemical determination of acyclic structures based on carbon−Proton spin-coupling constants. A method of configuration analysis for natural products. J. Org. Chem. 1999, 64, 866–876.
- Cimino, P.; Bifulco, G.; Evidente, A.; Abouzeid, M.; Riccio, R.; Gomez-Paloma, L. Extension of the J-Based configuration analysis to multiple conformer equilibria: An application to sapinofuranone A. Org. Lett. 2002, 4, 2779–2782.
- Boot, C.M.; Gassner, N.C.; Compton, J.E.; Tenney, K.; Tamble, C.M.; Lokey, R.S.; Holman, T.R.; Crews, P. Pinpointing pseurotins from a marine-derived Aspergillus as tools for chemical genetics using a synthetic lethality yeast screen. J. Nat. Prod. 2007, 70, 1672–1675.
- Menche, D.; Arikan, F.; Perlova, O.; Horstmann, N.; Ahlbrecht, W.; Wenzel, S.C.; Jansen, R.; Irschik, H.; Müller, R. Stereochemical determination and complex biosynthetic assembly of etnangien, a highly potent RNA polymerase inhibitor from the myxobacterium Sorangium cellulosum. J. Am. Chem. Soc. 2008, 130, 14234–14243.
- Matsumori, N.; Murata, M.; Tachibana, K. Conformational analysis of natural products using long-range carbon-proton coupling constants: Three-dimensional structure of okadaic acid in solution. Tetrahedron 1995, 51, 12229–12238.
- Bifulco, G.; Dambruoso, P.; Gomez-Paloma, L.; Riccio, R. Determination of relative configuration in organic compounds by NMR spectroscopy and computational methods. Chem. Rev. 2007, 107, 3744–3779.
- Kurz, M.; Schmieder, P.; Kessler, H. HETLOC, an efficient method for determining heteronuclear long-range couplings with heteronuclei in natural abundance. Angew. Chem. Int. Ed. 1991, 30, 1329–1331.
- Zhu, G.; Live, D.; Bax, A. Analysis of sugar puckers and glycosidic torsion angles in a DNA G-tetrad structure by heteronuclear three-bond J couplings. J. Am. Chem. Soc. 1994, 116, 8370–8371.
- Zhu, G.; Bax, A. Measurement of long-range 1H-13C coupling constants from quantitative 2D heteronuclear multiple-quantum correlation spectra. J. Magn. Reson. Ser. A 1993, 104, 353–357.
- Bassarello, C.; Bifulco, G.; Zampella, A.; D’Auria, M.V.; Riccio, R.; Gomez-Paloma, L. Stereochemical studies on sphinxolide: Advances in the J-based NMR determination of the relative configuration of flexible systems. Eur. J. Org. Chem. 2001, 2001, 39–44.
- Hwang, B.S.; Yoon, E.Y.; Jeong, E.J.; Park, J.; Kim, E.H.; Rho, J.R. Determination of the absolute configuration of polyhydroxy compound ostreol B isolated from the dinoflagellate Ostreopsis cf. ovata. J. Org. Chem. 2018, 83, 194–202.
- Dale, J.A.; Mosher, H.S. Nuclear magnetic resonance enantiomer regents. Configurational correlations via nuclear magnetic resonance chemical shifts of diastereomeric mandelate, O-methylmandelate, and .alpha.-methoxy-.alpha.- trifluoromethylphenylacetate (MTPA) esters. J. Am. Chem. Soc. 1973, 95, 512–519.
- Sullivan, G.R.; Dale, J.A.; Mosher, H.S. Correlation of configuration and fluorine-19 chemical shifts of .alpha.-methoxy-.alpha.-trifluoromethylphenyl acetate derivatives. J. Org. Chem. 1973, 38, 2143–2147.
- Latypov, S.K.; Seco, J.M.; Quinoa, E.; Riguera, R. Conformational structure and dynamics of arylmethoxyacetates: DNMR spectroscopy and aromatic shielding effect. J. Org. Chem. 1995, 60, 504–515.
- Ohtani, I.; Kusumi, T.; Kashman, Y.; Kakisawa, H. A new aspect of the high-field NMR application of Mosher’s method. The absolute configuration of marine triterpene sipholenol A. J. Org. Chem. 1991, 56, 1296–1298.
- Ohtani, I.; Kusumi, T.; Ishitsuka, M.O.; Kakisawa, H. Absolute configurations of marine diterpenes possessing a xenicane skeleton. An application of an advanced mosher’s method. Tetrahedron Lett. 1989, 30, 3147–3150.
- Hoye, T.R.; Jeffrey, C.S.; Shao, F. Mosher ester analysis for the determination of absolute configuration of stereogenic (chiral) carbinol carbons. Nat. Protoc. 2007, 2, 2451–2458.
- Ohtani, I.; Kusumi, T.; Kashman, Y.; Kakisawa, H. High-field FT NMR application of Mosher’s method. The absolute configurations of marine terpenoids. J. Am. Chem. Soc. 1991, 113, 4092–4096.
- Sakamoto, T.; Kondo, Y.; Sato, S.; Yamanaka, H. Total synthesis of a marine alkaloid, rigidin. Tetrahedron Lett. 1994, 35, 2919–2920.
- Teng, R.W.; Shen, P.; Wang, D.Z.; Yang, C.Z. Methods to determine the absolute stereochemistry of organic compounds by NMR spectroscopy. Chin. J. Magn. Reson. 2002, 19, 203–223.
- Fukushi, Y.; Yajima, C.; Mizutani, J. A new method for establishment of absolute configurations of secondary alcohols by NMR spectroscopy. Tetrahedron Lett. 1994, 35, 599–602.
- Harada, K.; Shimizu, Y.; Fujii, K. A chiral anisotropic reagent for determination of the absolute configuration of a primary amino compound. Tetrahedron Lett. 1998, 39, 6245–6248.
- Nagai, Y.; Kusumi, T. New chiral anisotropic reagents for determining the absolute configuration of carboxylic acids. Tetrahedron Lett. 1995, 36, 1853–1856.
- Seco, J.M.; Quiñoá, E.; Riguera, R. The assignment of absolute configuration by NMR. Chem. Rev. 2004, 104, 17–117.
- Latypov, S.K.; Seco, J.M.; Quiñoá, E.; Riguera, R. MTPA vs MPA in the determination of the absolute configuration of chiral alcohols by 1H NMR. J. Org. Chem. 1996, 61, 8569–8577.
- Bertin, M.J.; Saurí, J.; Liu, Y.Z.; Via, C.W.; Roduit, A.F.; Williamson, R.T. Trichophycins B–F, chlorovinylidene-containing polyketides isolated from a cyanobacterial bloom. J. Org. Chem. 2018, 83, 13256–13266.
- Zhu, S.; Sun, M. Electronic circular dichroism and Raman optical activity: Principle and applications. Appl. Spectrosc. Rev. 2021, 56, 553–587.
- Mándi, A.; Kurtán, T. Applications of OR/ECD/VCD to the structure elucidation of natural products. Nat. Prod. Rep. 2019, 36, 889–918.
- Harada, N.; Nakanishi, K. Exciton chirality method and its application to configurational and conformational studies of natural products. Acc. Chem. Res. 1972, 5, 257–263.
- Pescitelli, G. ECD exciton chirality method today: A modern tool for determining absolute configurations. Chirality 2022, 34, 333–363.
- Matile, S.; Berova, N.; Nakanishi, K.; Fleischhauer, J.; Woody, R.W. Structural studies by exciton coupled circular dichroism over a large distance: Porphyrin derivatives of steroids, dimeric steroids, and brevetoxin B. J. Am. Chem. Soc. 1996, 118, 5198–5206.
- Harada, N.; Berova, N. Spectroscopic analysis: Exciton circular dichroism for chiral analysis. Compr. Chirality 2012, 8, 449–477.
- Satake, M.; Tanaka, Y.; Ishikura, Y.; Oshima, Y.; Naoki, H.; Yasumoto, T. Gymnocin-B with the largest contiguous polyether rings from the red tide dinoflagellate, Karenia (formerly Gymnodinium) mikimotoi. Tetrahedron Lett. 2005, 46, 3537–3540.
- Tanaka, K.; Itagaki, Y.; Satake, M.; Naoki, H.; Yasumoto, T.; Nakanishi, K.; Berova, N. Three challenges toward the assignment of absolute configuration of gymnocin-B. J. Am. Chem. Soc. 2005, 127, 9561–9570.
- Snatzke, G.; Wagner, U.; Wolff, H.P. Circular dichroism—LXXV1: Cottonogenic derivatives of chiral bidentate ligands with the complex . Tetrahedron 1981, 37, 349–361.
- Górecki, M.; Jabłońska, E.; Kruszewska, A.; Suszczyńska, A.; Urbańczyk-Lipkowska, Z.; Gerards, M.; Morzycki, J.W.; Szczepek, W.J.; Frelek, J. Practical method for the absolute configuration assignment of tert/tert 1,2-diols using their complexes with Mo2(OAc)4. J. Org. Chem. 2007, 72, 2906–2916.
- Frelek, J.; Ruśkowska, P.; Suszczyńska, A.; Szewczyk, K.; Osuch, A.; Jarosz, S.; Jagodziński, J. Configurational assignment of sugar erythro-1,2-diols from their electronic circular dichroism spectra with dimolybdenum tetraacetate. Tetrahedron Asymmetry 2008, 19, 1709–1713.
- Bari, D.; Pescitelli, G.; Pratelli, C.; Pini, D.; Salvadori, P. Determination of absolute configuration of acyclic 1,2-diols with Mo2(OAc)4. 1′ Snatzke’s Method Revisited. J. Org. Chem. 2001, 66, 4819–4825.
- Bai, J.; Liu, D.; Yu, S.; Proksch, P.; Lin, W. Amicoumacins from the marine-derived bacterium Bacillus sp. with the inhibition of NO production. Tetrahedron Lett. 2014, 55, 6286–6291.
- Gerards, M.; Snatzke, G. Circular dichroism, XCIII determination of the absolute configuration of alcohols, olefins, epoxides, and ethers from the CD of their “in situ” complexes with . Tetrahedron Asymmetry 1990, 1, 221–236.
- Frelek, J.; Szczepek, W.J. as an auxiliary chromophore in chiroptical studies on steroidal alcohols. Tetrahedron Asymmetry 1999, 10, 1507–1520.
- Frelek, J.; Jagodziński, J.; Meyer-Figge, H.; Sheldrick, W.S.; Wieteska, E.; Szczepek, W.J. Chiroptical properties of binuclear rhodium complexes of lanostane alcohols. Chirality 2001, 13, 313–321.
- Zhang, F.; Barns, K.; Hoffmann, F.M.; Braun, D.R.; Andes, D.R.; Bugni, T.S. Thalassosamide, a siderophore discovered from the marine-derived bacterium Thalassospira profundimaris. J. Nat. Prod. 2017, 80, 2551–2555.
- Santoro, E.; Vergura, S.; Scafato, P.; Belviso, S.; Masi, M.; Evidente, A.; Superchi, S. Absolute configuration assignment to chiral natural products by biphenyl chiroptical probes: The case of the phytotoxins colletochlorin A and agropyrenol. J. Nat. Prod. 2020, 83, 1061–1068.
- Marsico, G.; Calice, U.; Scafato, P.; Belviso, S.; Evidente, A.; Superchi, S. Computational approaches and use of chiroptical probes in the absolute configuration assignment to natural products by ECD spectroscopy: A 1,2,3-trihydroxy-p-menthane as a case study. Biomolecules 2022, 12, 421.
- Wolf, C.; Bentley, K.W. Chirality sensing using stereodynamic probes with distinct electronic circular dichroism output. Chem. Soc. Rev. 2013, 42, 5408–5424.
- Superchi, S.; Scafato, P.; Gorecki, M.; Pescitelli, G. Absolute configuration determination by quantum mechanical calculation of chiroptical spectra: Basics and applications to fungal metabolites. Curr. Med. Chem. 2018, 25, 287–320.
- Berova, N.; Pescitelli, G.; Petrovic, A.G.; Proni, G. Probing molecular chirality by CD-sensitive dimeric metalloporphyrin hosts. Chem. Commun. 2009, 40, 5958–5980.
- Barone, G.; Gomez-Paloma, L.; Duca, D.; Silvestri, A.; Riccio, R.; Bifulco, G. Structure validation of natural products by quantum-mechanical GIAO calculations of 13C NMR chemical shifts. Chemistry 2002, 8, 3233–3239.
- Meiler, J.; Sanli, E.; Junker, J.; Meusinger, R.; Lindel, T.; Will, M.; Maier, W.; Köck, M. Validation of structural proposals by substructure analysis and 13C NMR chemical shift prediction. J. Chem. Inf. Comput. Sci. 2002, 42, 241–248.
- Bagno, A. Complete prediction of the 1H NMR spectrum of organic molecules by DFT calculations of chemical shifts and spin–Spin coupling constants. Chem. Eur. J. 2001, 7, 1652–1661.
- Forsyth, D.A.; Sebag, A.B. Computed 13C NMR chemical shifts via empirically scaled GIAO shieldings and molecular mechanics geometries. Conformation and configuration from 13C shifts. J. Am. Chem. Soc. 1997, 119, 9483–9494.
- Lodewyk, M.W.; Siebert, M.R.; Tantillo, D.J. Computational prediction of 1H and 13C chemical shifts: A useful tool for natural product, mechanistic, and synthetic organic chemistry. Chem. Rev. 2012, 112, 1839–1862.
- Costa, F.L.P.; Albuquerque, A.C.F.; Fiorot, R.G.; Lião, L.M.; Martorano, L.H.; Mota, G.V.S.; Valverde, A.L.; Carneiro, J.W.M.; Junior, F.M.S. Structural characterisation of natural products by means of quantum chemical calculations of NMR parameters: New insights. Org. Chem. Front. 2021, 8, 2019–2058.
- Kim, C.S.; Oh, J.; Lee, T.H. Structure elucidation of small organic molecules by contemporary computational chemistry methods. Arch. Pharm. Res. 2020, 43, 1114–1127.
- Marcarino, M.O.; Cicetti, S.; Zanardi, M.M.; Sarotti, A.M. A critical review on the use of DP4+ in the structural elucidation of natural products: The good, the bad and the ugly. A practical guide. Nat. Prod. Rep. 2022, 39, 58–76.
- Smith, S.G.; Goodman, J.M. Assigning stereochemistry to single diastereoisomers by GIAO NMR calculation: The DP4 probability. J. Am. Chem. Soc. 2010, 132, 12946–12959.
- Ermanis, K.; Parkes, K.E.; Agback, T.; Goodman, J.M. Expanding DP4: Application to drug compounds and automation. Org. Biomol. Chem. 2016, 14, 3943–3949.
- Howarth, A.; Ermanis, K.; Goodman, J.M. DP4-AI automated NMR data analysis: Straight from spectrometer to structure. Chem. Sci. 2020, 11, 4351–4359.
- Grimblat, N.; Zanardi, M.M.; Sarotti, A.M. Beyond DP4: An improved probability for the stereochemical assignment of isomeric compounds using quantum chemical calculations of NMR shifts. J. Org. Chem. 2015, 80, 12526–12534.
- Grimblat, N.; Gavín, J.A.; Daranas, A.H.; Sarotti, A.M. Combining the power of J coupling and DP4 analysis on stereochemical assignments: The J-DP4 methods. Org. Lett. 2019, 21, 4003–4007.
- Zanardi, M.M.; Marcarino, M.O.; Sarotti, A.M. Redefining the impact of boltzmann analysis in the stereochemical assignment of polar and flexible molecules by NMR calculations. Org. Lett. 2020, 22, 52–56.
- Hehre, W.; Klunzinger, P.; Deppmeier, B.; Driessen, A.; Uchida, N.; Hashimoto, M.; Fukushi, E.; Takata, Y. Efficient protocol for accurately calculating 13C chemical shifts of conformationally flexible natural products: Scope, Assessment, and Limitations. J. Nat. Prod. 2019, 82, 2299–2306.
- Cornilescu, G.; Alvarenga, R.F.R.; Wyche, T.P.; Bugni, T.S.; Gil, R.R.; Cornilescu, C.C.; Westler, W.M.; Markley, J.L.; Schwieters, C.D. Progressive stereo locking (PSL): A residual dipolar coupling based force field method for determining the relative configuration of natural products and other small molecules. ACS Chem. Biol. 2017, 12, 2157–2163.
- Tzvetkova, P.; Sternberg, U.; Gloge, T.; Navarro-Vázquez, A.; Luy, B. Configuration determination by residual dipolar couplings: Accessing the full conformational space by molecular dynamics with tensorial constraints. Chem. Sci. 2019, 10, 8774–8791.
- Immel, S.; Köck, M.; Reggelin, M. NMR-based configurational assignments of natural products: Gibbs sampling and bayesian inference using floating chirality distance geometry calculations. Mar. Drugs 2022, 20, 14.
- Hallwass, F.; Schmidt, M.; Sun, H.; Mazur, A.; Kummerlöwe, G.; Luy, B.; Navarro-Vázquez, A.; Griesinger, C.; Reinscheid, U.M. Residual chemical shift anisotropy (RCSA): A tool for the analysis of the configuration of small molecules. Angew. Chem. Int. Ed. 2011, 50, 9487–9490.
- Liu, Y.; Saurí, J.; Mevers, E.; Peczuh, M.W.; Hiemstra, H.; Clardy, J.; Martin, G.E.; Williamson, R.T. Unequivocal determination of complexmolecular structures using anisotropic NMR measurements. Science 2017, 356, eaam5349.
- Li, G.W.; Liu, H.; Qiu, F.; Wang, X.J.; Lei, X.X. Residual dipolar couplings in structure determination of natural products. Nat. Prod. Bioprospect. 2018, 8, 279–295.
- Liu, Y.; Navarro-Vázquez, A.; Gil, R.R.; Griesinger, C.; Martin, G.E.; Williamson, R.T. Application of anisotropic NMR parameters to the confirmation of molecular structure. Nat. Protoc. 2019, 14, 217–247.
- Li, X.L.; Chi, L.P.; Navarro-Vázquez, A.; Hwang, S.; Schmieder, P.; Li, X.M.; Li, X.; Yang, S.Q.; Lei, X.X.; Wang, B.G.; et al. Stereochemical elucidation of natural products from residual chemical shift anisotropies in a liquid crystalline phase. J. Am. Chem. Soc. 2020, 142, 2301–2309.
- Pescitelli, G.; Bruhn, T. Good computational practice in the assignment of absolute configurations by TDDFT calculations of ECD spectra. Chirality 2016, 28, 466–474.
- Huang, R.; Liang, L.; Guo, Y. Time-dependent density functional theory electronic circular dichroism (TDDFT ECD) calculation as a promising tool to determine the absolute configuration of natural products. J. Int. Pharm. Res. 2015, 42, 686–698.
- McCann, D.M.; Stephens, P.J. Determination of absolute configuration using density functional theory calculations of optical rotation and electronic circular dichroism: Chiral alkenes. J. Org. Chem. 2006, 71, 6074–6098.
- Liu, Z.; Wang, Q.; Li, S.; Cui, H.; Sun, Z.; Chen, D.; Lu, Y.; Liu, H.; Zhang, W. Polypropionate derivatives with mycobacterium tuberculosis protein tyrosine phosphatase B inhibitory activities from the deep-sea-derived fungus Aspergillus fischeri FS452. J. Nat. Prod. 2019, 82, 3440–3449.
- Stephens, P.J.; Devlin, F.J.; Pan, J.J. The determination of the absolute configurations of chiral molecules using vibrational circular dichroism (VCD) spectroscopy. Chirality 2008, 20, 643–663.
- Felippe, L.G.; Batista, J.M.; Baldoqui, D.C.; Nascimento, I.R.; Kato, M.J.; He, Y.; Nafie, L.A.; Furlan, M. VCD to determine absolute configuration of natural product molecules: Secolignans from Peperomia blanda. Org. Biomol. Chem. 2012, 10, 4208–4214.
- Gussem, E.D.; Herrebout, W.; Specklin, S.; Meyer, C.; Cossy, J.; Bultinck, P. Strength by joining methods: Combining synthesis with NMR, IR, and Vibrational Circular Dichroism spectroscopy for the determination of the relative configuration in hemicalide. Chem. Eur. J. 2014, 20, 17385–17394.
- MacGregor, C.I.; Han, B.Y.; Goodman, J.M.; Paterson, I. Toward the stereochemical assignment and synthesis of hemicalide: DP4f GIAO-NMR analysis and synthesis of a reassigned C16–C28 subunit. Chem. Commun. 2016, 52, 4632–4635.
- Han, B.Y.; Lam, N.Y.S.; MacGregor, C.I.; Goodman, J.M.; Paterson, I. A synthesis-enabled relative stereochemical assignment of the C1–C28 region of hemicalide. Chem. Commun. 2018, 54, 3247–3250.
- Satake, M.; Murata, M.; Yasumoto, T.; Fujita, T.; Naoki, H. Amphidinol, a polyhydroxy-polyene antifungal agent with an unprecedented structure, from a marine dinoflagellate, Amphidinium klebsii. J. Am. Chem. Soc. 1991, 113, 9859–9861.
- Murata, M.; Matsuoka, S.; Matsumori, N.; Paul, G.K.; Tachibana, K. Absolute configuration of amphidinol 3, the first complete structure determination from amphidinol homologues: Application of a new configuration analysis based on carbon-hydrogen spin-coupling constants. J. Am. Chem. Soc. 1999, 121, 870–871.
- Wakamiya, Y.; Ebine, M.; Murayama, M.; Omizu, H.; Matsumori, N.; Murata, M.; Oishi, T. Synthesis and stereochemical revision of the C31–C67 fragment of amphidinol 3. Angew. Chem. Int. Ed. 2018, 57, 6060–6064.
- Makarieva, T.N.; Ivanchina, N.V.; Stonik, V.A. Application of oxidative and reductive transformations in the structure determination of marine natural products. J. Nat. Prod. 2020, 83, 1314–1333.
- Seibert, S.F.; Eguereva, E.; Krick, A.; Kehraus, S.; Voloshina, E.; Raabe, G.; Fleischhauer, J.; Leistner, E.; Wiese, M.; Prinz, H. Polyketides from the marine-derived fungus Ascochyta salicorniae and their potential to inhibit protein phosphatases. Org. Biomol. Chem. 2006, 4, 2233–2240.
- Kobayashi, J.; Sato, M.; Ishibashi, M. Amphidinolide J: A cytotoxic macrolide from the marine dinoflagellate Amphidinium sp. Determination of the absolute stereochemistry. J. Org. Chem. 1993, 58, 2645–2646.
- Imperatore, C.; Luciano, P.; Aiello, A.; Vitalone, R.; Irace, C.; Santamaria, R.; Li, J.; Guo, Y.W.; Menna, M. Structure and configuration of phosphoeleganin, a protein tyrosine phosphatase 1B inhibitor from the mediterranean ascidian Sidnyum elegans. J. Nat. Prod. 2016, 79, 1144–1148.
More
Information
Subjects:
Spectroscopy
Contributor
MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register
:
View Times:
1.5K
Revisions:
3 times
(View History)
Update Date:
01 Jun 2022
Notice
You are not a member of the advisory board for this topic. If you want to update advisory board member profile, please contact office@encyclopedia.pub.
OK
Confirm
Only members of the Encyclopedia advisory board for this topic are allowed to note entries. Would you like to become an advisory board member of the Encyclopedia?
Yes
No
${ textCharacter }/${ maxCharacter }
Submit
Cancel
Back
Comments
${ item }
|
More
No more~
There is no comment~
${ textCharacter }/${ maxCharacter }
Submit
Cancel
${ selectedItem.replyTextCharacter }/${ selectedItem.replyMaxCharacter }
Submit
Cancel
Confirm
Are you sure to Delete?
Yes
No




