Your browser does not fully support modern features. Please upgrade for a smoother experience.

Submitted Successfully!
Thank you for your contribution! You can also upload a video entry or images related to this topic.
For video creation, please contact our Academic Video Service.
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Kallol Biswas | + 2085 word(s) | 2085 | 2021-10-27 06:18:36 | | | |
| 2 | Conner Chen | + 26 word(s) | 2111 | 2021-11-04 02:19:35 | | | | |
| 3 | Conner Chen | + 26 word(s) | 2111 | 2021-11-04 02:26:07 | | | | |
| 4 | Conner Chen | Meta information modification | 2111 | 2021-11-05 07:29:37 | | |
Video Upload Options
We provide professional Academic Video Service to translate complex research into visually appealing presentations. Would you like to try it?
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Biswas, K. New Generation Metaheuristic Algorithms. Encyclopedia. Available online: https://encyclopedia.pub/entry/15673 (accessed on 13 January 2026).
Biswas K. New Generation Metaheuristic Algorithms. Encyclopedia. Available at: https://encyclopedia.pub/entry/15673. Accessed January 13, 2026.
Biswas, Kallol. "New Generation Metaheuristic Algorithms" Encyclopedia, https://encyclopedia.pub/entry/15673 (accessed January 13, 2026).
Biswas, K. (2021, November 03). New Generation Metaheuristic Algorithms. In Encyclopedia. https://encyclopedia.pub/entry/15673
Biswas, Kallol. "New Generation Metaheuristic Algorithms." Encyclopedia. Web. 03 November, 2021.
Copy Citation
Metaheuristics are the special branch of heuristic methods that can explore a whole problem space with different heuristic approaches by a replicated intelligent iterative process. Normally, metaheuristics stimulate the natural evolution strategy to produce convergence, which needs less parameters to tune for any certain problem. This is why metaheuristic has been implemented to large instance NP-hard problems, which leads to a similar optimization like the exact methods.
metaheuristic optimization
combinatorial
supply chain
vehicle routing
artrificial intelligence
travelling salesman
operation research
soft computing
1. Firefly Algorithm (FA)
A new population-based metaheuristic in resolving questions related to continuous optimization is the firefly algorithm (FA). FA was inspired by the simulation of the social light flashing behavior of the fireflies. Fireflies emit light and their light intensity variation differentiates among each firefly’s identity.
The firefly algorithm follows these rules:
-
Every firefly will attract each other beyond considerations of sex.
-
A firefly having high brightness can attract a less bright firefly, and a brighter firefly has the scope to move to the next position quicker than the less bright firefly. Eventually, the objective function can be considered as the light intensity of a firefly.(1)Here, Cx=cost function and Ix=light intensity
-
For two fireflies where the first one has less light intensity than the other, the first firefly moves in the direction of a brighter firefly and updates the solution. The following formula can describe this event:where x′i = new position of firefly, α = mutation coefficient (takes the value 0–1); β = attraction co-efficient (normally the value is 1; δ = light absorption coefficient (value range is 0.01–100)). These values are recommended by the inventor of FA [1].
FA has the ability to categorize fireflies into several small groups due to its inherent subdivision capability. This is the main reason why FA can handle multimodal and non-linear problems so well. FA’s position updates the direction; on the other hand, it is mostly single-dimensional as well as diagonal. In fact, FA cannot search in a regional direction, resulting in increased computational complexity and poor diversification [2]. So, several researchers have adopted modified FA with incorporation of encoding mechanism in FA’s classical framework. For example, Trachanatzi et al. [3] designed a modified firefly algorithm on a VRP to find maximum prize collection with a minimum carbon emission factor. This modified FA has outperformed Differential Evolution (DE), Bat Algorithm (BA) and Gurobi optimizer claimed by the authors.
The basic framework of FA is illustrated in Figure 1.

Figure 1. Flowchart of the firefly algorithm [4].
2. Harmony Search Algorithm (HS)
The harmony search concept is derived by musicians looking for the best harmonious result in harmony improvising. The improvisation method of musical harmony usually comprises three steps: first, selecting a suitable pitch of music from the memory of the musicians; second, a pitch of music related to a reasonable pitch that is slightly tweakable and formulating a new or random pitch. The aforementioned musical harmony improvisation strategy was first discussed by Geem et al. [5]. Similar to other nature-inspired metaheuristics, HS also replicates the elitist rule. A group of better-quality harmonies is considered, and weak sets of harmony are withdrawn from the process. The process continues until any optimum harmony is attained. The HS algorithm mechanism can be demonstrated by the following steps: initialization of harmony memory, formulating new vectors for the new solution (applying a two-stage probability-based harmony memory). The HS algorithm’s core tweakable factors are pitch adjustment probability (PAR) along with the retention probability of harmony memory [6]. Here, the PAR ensures the local search capabilities of the vectors around sub problem space. Eventually, the recommended value of PAR has been stated as 0.1–0.5 and for HMCR is 0.7–0.95 by Geem et al. [5] for a wide number of cases. Moreover, retention probability index HMCR has an important impact on optimality finding for HS algorithm. It has been observed that the higher number of HMCR leads to having a better probability for searching optimal solution [7]. The small value of HMCR tends to provide precise solutions, but it takes higher computational time to provide that solution. This is why choosing a balanced value of HMCR can really impact the performance of HS algorithm in different problem instances. Figure 2 shows a visual representation of the harmony search algorithm mechanism.
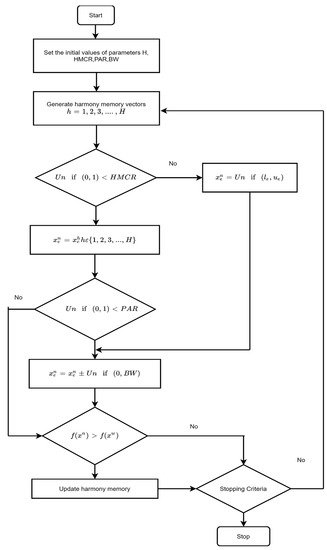
Figure 2. Framework of Harmony Search.
3. Bat Algorithm
The Bat Algorithm is a nature memetic algorithm introduced by Yang (2010). This metaheuristic approach follows an echolocation-based technique including randomization, secondly updating the position along with comparison of the best outcomes.
Many of the metaheuristic techniques have a common criterion as they follow a randomization process to update the solution process in a certain dimension. Though in real life, bats move randomly to their food or prey; in a defined dimension, their randomization value becomes skeptical [8].
In every generation, the bats provide the information of frequency and velocity and prepare a new solution. The update of solution can be illustrated by the following equations
where fmin and fmax denotes the minimum and maximum frequency of the bats while vti represents the velocity of a bat at time t. Eventually, the Bat Algorithm follows the echolocation technique, which means whenever a bat is nearer to a prey, the loudness factor Ai and pulse emission rate r is updated. The relation is vice versa whenever a solution update and loudness value (A) decreases, and the pulse emission rate increases at a time. The following equations can describe this phenomenon:
In the above-mentioned equations, α and γ are constants; Ai , ri represents initial loudness and pulse rate consecutively. BA’s working mechanism is represented in Figure 3.

Figure 3. Framework of the Bat Algorithm.
It has been observed that the Bat Algorithm has been evolved with several tuning in pulse frequency range factor with an application perspective [9]. Moreover, BA has a normal tendency to be trapped into local optima. To resolve this issue, researchers have implemented several manipulations in standard BA, the like levy flight technique, instead of a conventional step walk or swarm techniques in the local search stage and inertia weight for velocity update. Table 1 shows the pulse frequency setting preferred by different researchers.
Table 1. The different pulse frequency ranges implemented by the researchers for the Standard BA modification.
| Authors | Pulse Frequency Range |
|---|---|
| [10] | 0–1 |
| [11] | 0–2 |
| [12] | 0–5 |
| [13] | 0–100 |
4. Cuckoo Search (CS)
The Cuckoo Search is an evolutionary algorithm that follows the trade-off between randomization and local search like other metaheuristics. Having a minimal parameter to work with it, CS has been widely used by the researchers as it needs less effort for parameter initialization. Compared to other population-based metaheuristics, for example, GA, PSO, and CS have shown improved performance for their simplicity in an algorithm-built nature [14].
The Cuckoo Search was evolved by X. S. Yang and Deb [15] through adopting an enhanced type of random walk, named the Lévy Flight, rather than isotropic random walk. Several nature creations have Lévy flight behavior and inventors were inspired by the performance of Lévy flights because it has infinite mean variance and has better exploration capabilities, rather than standard Gaussian processes [16].
Having a predatory reproduction strategy of some Cuckoo species, the Cuckoo Search is the representation of brood parasitism. In nature, some of the species do not build their own nests and rather than they choose nest from another species to camouflage their eggs to continue their reproduction. In contrast to other birds’ laying eggs strategies, the Cuckoo Search contains its individual trick to identify their eggs.
The standard Cuckoo Search has three distinguished rules, which activates the following:
-
Each cuckoo lays one egg at a time and puts it a nest selected randomly.
-
The best nests would follow the elitist strategy and best quality nest will carry forward to the following generations.
-
There would be a fixed number of available host nests and the egg discovery probability by the host bird can be expressed as paϵ(0,1).
The Cuckoo Search follows an integration of a local random walk and a global explorative random walk where a switching parameter pa guides the walk. The following equation can represent the local random walk:
where xtj and xtk are selected different solutions are sorted by random permutation, ϵ is a random number from uniform distribution along with s represents step size. As per the second strategy of CS, the global random walk will follow the equation below:
It has been observed that when the step size scaling factor α=O(L100), CS works more effectively and ignores excessive exploration [16]. A complete framework of CS algorithm will be represented by following Figure 4.
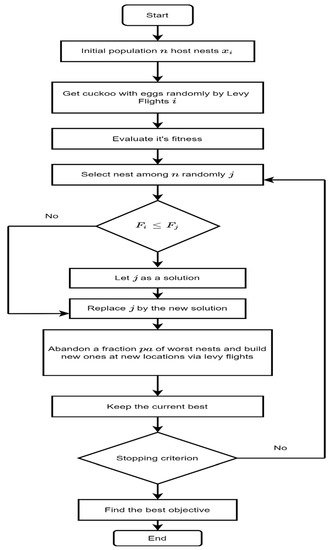
Figure 4. Framework of the standard Cuckoo Search (CS) Algorithm.
5. Artificial Bee Colony (ABC) Algorithm
The Artificial Bee Colony (ABC) algorithm simulates honeybee drinking behavior and was applied to many realistic problems. This optimization technique is used. ABC was proposed by Karaboga [17] and it is a part of the swarm intelligence group of metaheuristic algorithms.
The ABC algorithm works in a certain way by having three different categories of bees assigned for the execution. Consecutively, predefined bees tend to search around a food source or feasible solution. The onlooker bees measure the objective function values and sort out the food source with respect to nectar amount. This metaheuristic technique also has the elitist mechanism, as after a certain number of trials, if the function value remains stuck in the previous value, a new food source has been added by the scout bees to formulate a better solution for a certain objective function [18]. In brief, the ABC algorithm performs three phases in every evaluation as follows: (1) employed bee phase or local search phase, (2) onlooker phase, (3) conducting global search phase recognized as scout bee phase. Figure 5 describes the mechanism of the ABC algorithm.
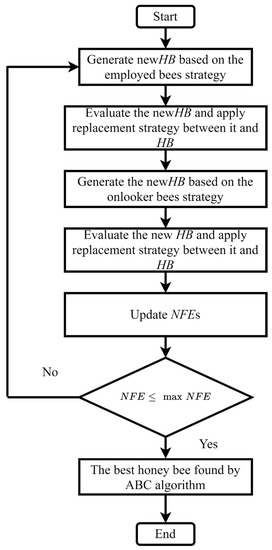
Figure 5. Framework of Artificial Bee Colony Algorithm [19].
5. Bacterial Foraging Algorithm (BFOA)
BFOA is structured on a group foraging strategy from E. coli bacteria swarm instances. Bacteria prefer to look for nutrients to thrive in a harsh environment in such a way as to enhance the energy obtained per unit time. A bacterial foraging algorithm was proposed by Passino [20] from the natural phenomena of bacteria swarms. During the foraging process, a group of tensile flagella initiates locomotion where E. coli bacteria can swim or tumble around the cell. While the direction of flagella is clockwise, that particular flagella hold strictly a cell around it with having lesser tumble movement. On the other hand, the counterclockwise direction enables quick swimming motion for the flagella’s better exploration.
6. NSGA-2 (Non-Dominated Sorting Genetic Algorithm-2)
NSGA-2 has been the most profound algorithm with respect to its application in multi-objective optimization. Basically, NSGA-2 was the updated version of NSGA, which was first introduced by Deb et al. [21]. Moreover, NSGA-2 was designed to overcome the difficulties faced by the NSGA algorithm, such as more computational complexity, parameter tuning difficulty, and the absence of perfect elitism. Due to the robustness of NSGA-2 while optimizing complex problems, it has become the most popular approach in MOO.
NSGA-2 works on a random population and the solution gets enriched by the chronological iterations. The progress over iteration can be expressed by the change of fitness value in each iteration. Later, the population tends to create the Pareto front with non-domination sorting technique (where the first Pareto can be considered as smallest rank, and it is updated as the cardinal way). Every single solution of the population can be expressed as chromosomes that can hold binary values or real values. Then, each member’s Pareto front distance is calculated by the linear distance metric. NSGA-2 follows the elitist mechanism, which is why the crowding distance and both ranks should be measured in each population by the selection operator. While selecting two members, the least ranked member was counted. However, if two members hold the same rank, the member with the better crowding distance gets selected.
Normally, NSGA-2 adopts the same stages as Genetic Algorithms, such as selection, crossover, and mutation. Initially, an offspring population, Q-t, is formulated from the parent population, P-t. To build an intermediate population of 2N, the offspring population gets integrated with the parent population. In every iteration, fitness value is calculated according to the objective function value. Later on, multiple members are selected through several selection criteria. This process continues until the termination condition is occupied. At the end of the whole process, a set of nondominant Pareto solutions are formed, which are the best at every aspect of a multi-objective optimization. The NSGA-2 algorithm is illustrated in Figure 6.

Figure 6. Framework of the NSGA-2 algorithm.
References
- Yang, X.-S. Firefly algorithm, Levy flights and global optimization. In Research and Development in Intelligent Systems XXVI; Springer: Berlin/Heidelberg, Germany, 2010; pp. 209–218.
- Osaba, E.; Yang, X.-S.; Diaz, F.; Onieva, E.; Masegosa, A.D.; Perallos, A. A discrete firefly algorithm to solve a rich vehicle routing problem modelling a newspaper distribution system with recycling policy. Soft Comput. 2016, 21, 5295–5308.
- Trachanatzi, D.; Rigakis, M.; Marinaki, M.; Marinakis, Y. A firefly algorithm for the environmental prize-collecting vehicle routing problem. Swarm Evol. Comput. 2020, 57, 100712.
- Arora, J.S. Introduction to optimization. In Optimization of Structural and Mechanical Systems; Elsevier: Amsterdam, The Netherlands, 2007; pp. 1–34. ISBN 9789812779670.
- Geem, Z.W.; Kim, J.H.; Loganathan, G. A New Heuristic Optimization Algorithm: Harmony Search. Simulation 2001, 76, 60–68.
- Shams, M.; El-Banbi, A.; Sayyouh, H. Harmony search optimization applied to reservoir engineering assisted history matching. Pet. Explor. Dev. 2020, 47, 154–160.
- Biswas, K.; Vasant, P.M.; Vintaned, J.A.G.; Watada, J. A Review of Metaheuristic Algorithms for Optimizing 3D Well-Path Designs. Arch. Comput. Methods Eng. 2021, 28, 1775–1793.
- Ramli, M.R.; Abas, Z.A.; Desa, M.I.; Abidin, Z.Z.; Alazzam, M.B. Enhanced convergence of Bat Algorithm based on dimensional and inertia weight factor. J. King Saud Univ. Inf. Sci. 2019, 31, 452–458.
- Wang, Y.; Wang, P.; Zhang, J.; Cui, Z.; Cai, X.; Zhang, W.; Chen, J. A Novel Bat Algorithm with Multiple Strategies Coupling for Numerical Optimization. Mathematics 2019, 7, 135.
- Hasançebi, O.; Teke, T.; Pekcan, O. A bat-inspired algorithm for structural optimization. Comput. Struct. 2013, 128, 77–90.
- Gandomi, A.H.; Yang, X.-S. Chaotic bat algorithm. J. Comput. Sci. 2014, 5, 224–232.
- Fister, I.; Fong, S.; Brest, J. A Novel Hybrid Self-Adaptive Bat Algorithm. Sci. World J. 2014, 2014, 1–12.
- Ali, E. Optimization of Power System Stabilizers using BAT search algorithm. Int. J. Electr. Power Energy Syst. 2014, 61, 683–690.
- Civicioglu, P.; Besdok, E. A conceptual comparison of the Cuckoo-search, particle swarm optimization, differential evolution and artificial bee colony algorithms. Artif. Intell. Rev. 2011, 39, 315–346.
- Yang, X.S.; Deb, S. Cuckoo search via Lévy flights. In Proceedings of the 2009 World Congress on Nature and Biologically Inspired Computing, NABIC 2009, Coimbatore, India, 9–11 December 2009; IEEE: Picataway, NJ, USA, 2009; pp. 210–214.
- Yang, X.-S.; Deb, S. Cuckoo search: Recent advances and applications. Neural Comput. Appl. 2014, 24, 169–174.
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization; Technical Report-TR06; Computer Engineering Department, Engineering Faculty, Erciyes University: Kayseri, Turkey, 2005; Volume 200, pp. 1–10.
- Samanta, S.; Philip, D.; Chakraborty, S. Bi-objective dependent location quadratic assignment problem: Formulation and solution using a modified artificial bee colony algorithm. Comput. Ind. Eng. 2018, 121, 8–26.
- Kaveh, A.; Bakhshpoori, T. Metaheuristics: Outlines, MATLAB Codes and Examples; Springer: Cham, Switzerland, 2019; ISBN 3030040674.
- Passino, K.M. Biomimicry of bacterial foraging for distributed optimization and control. IEEE Control. Syst. Mag. 2002, 22, 52–67.
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197.
More
Information
Contributor
MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register
:
View Times:
1.3K
Revisions:
4 times
(View History)
Update Date:
05 Nov 2021
Notice
You are not a member of the advisory board for this topic. If you want to update advisory board member profile, please contact office@encyclopedia.pub.
OK
Confirm
Only members of the Encyclopedia advisory board for this topic are allowed to note entries. Would you like to become an advisory board member of the Encyclopedia?
Yes
No
${ textCharacter }/${ maxCharacter }
Submit
Cancel
Back
Comments
${ item }
|
More
No more~
There is no comment~
${ textCharacter }/${ maxCharacter }
Submit
Cancel
${ selectedItem.replyTextCharacter }/${ selectedItem.replyMaxCharacter }
Submit
Cancel
Confirm
Are you sure to Delete?
Yes
No




