
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Lijesh Koottaparambil | + 1748 word(s) | 1748 | 2021-10-19 10:51:16 | | | |
| 2 | Nora Tang | Meta information modification | 1748 | 2021-11-03 08:46:14 | | | | |
| 3 | Nora Tang | Meta information modification | 1748 | 2021-11-03 08:48:45 | | | | |
| 4 | Nora Tang | Meta information modification | 1748 | 2021-11-03 08:49:50 | | | | |
| 5 | Lindsay Dong | Meta information modification | 1748 | 2021-11-12 09:17:47 | | |
Video Upload Options
According to the degradation-entropy generation (DEG) theorem, material degradation is irreversible and always accompanied by entropy generation. When applied to the degradation of a tribo-component, the DEG theorem relates the rate of change in wear volume to thermodynamic force via a parameter known as the degradation coefficient B. The efficacy of the B over the well-established Archard coefficient has been experimentally demonstrated for tribo-components that experience wear under running-in and steady-state operating conditions. The steady wear includes uni-directional, bi-directional, uniform, and variable operating conditions.
1. Introduction
Having analyzed 300+ models and equations describing wear and friction from 5466 reports, Meng and Ludema[1] concluded that no unified wear equation exists that can characterize various types of wear. Archard equation[2], the most widely accepted wear model, provides a satisfactory prediction for steady-state adhesive wear under dry operating conditions[3][4][5]. However, the quantitative predictions of the Archard equation for many processes—e.g., running-in[6], non-metals such as composites[7], situations that involve variable loading[8], etc.—tend to substantially deviate from measured values. The challenge in developing unified wear equations arises due to the dependence of the wear behavior on the operating conditions, interfacial adhesion/friction conditions, and the physical, chemical, and mechanical properties of the contacting pairs[9][10][11].
Recent research shows that different types of degradations—e.g., batteries[12], greases[13][14][15], mechanical fatigue[16], etc.—are always accompanied by the generation of entropy. The proof of concept studies[17][18][19][20] has also established that the degradation of the tribo-components by material removal can be characterized effectively using the framework of irreversible thermodynamics.
Considering the correlation between the degradation and entropy generation, Bryant et al[21] proposed a generalized theorem called degradation entropy generation (DEG) to characterize the degradation of materials. A proportionality coefficient called the degradation coefficient B emerged from the DEG theorem that directly related the irreversible degradation of the tribo-components to the entropy generation via the generalized entropy flow and degradation force. Amiri and Khonsari[22] and Bryant[23] discussed the possibilities of developing a unified wear model using the DEG theorem and B values for different wear processes[24]. However, until recently, sufficient experimental validation was lacking to demonstrate its efficacy in practice. In what follows, we show that the recent advances in tribology have largely addressed these limitations by both in-depth theoretical and experimental investigations.
As a first step towards developing a unified wear approach, the present work focuses on understanding different wear models and their capability in characterizing the degradation of tribo-pairs experiencing (i) uni-directional or bi-directional motions; (ii) uniform and variable operating conditions, and (iii) time-dependent or transient operating conditions, such as running-in.
2. Adhesive Wear Models
The adhesive wear mechanism was first investigated by Holm[25] for electric contacts from the perception of the real contact area. The volume of material loss wvol is considered proportional to the applied load P, sliding distance x, and inversely proportional to the hardness H of the softer material. The expression for wear volume is provided in Equation (1)

where k is a nondimensional proportionality constant called wear coefficient. Later Archard[2] and Rabinowicz[26] attributed the wear mechanism as the removal of particles due to the fracture of the junction itself. The wear equation introduced by Archard[2] (Equation 2) has the same form as Equation (1) and requires determining the wear coefficient K by performing pin-on-disk measurements. The parameter K is called the Archard wear coefficient. It is defined as “the probability that the asperities of the tribo-pair in sliding motion will deform plastically and wear out.” Archard equation has been extensively used to predict the wear of tribo-pairs in the sliding contact[9][11][27].

where V is the sliding speed. The values of K vary from 10−15 to 10−1, depending on the operating conditions and material properties. Welsh[28] and Vancoille[29] stated that the value of K varies up to two orders of magnitude, just by making small changes in the operating conditions. Such drastic variations in K values make it difficult to predict and validate experimental results. Researchers nowadays agree that a systematic study on the K values is needed to better understand and characterize the wear behavior of tribo-components[30].
Approaches considering the physical and chemical process of wear[31], and surface topography (fractal) parameters[32], including interfacial adhesion characteristics[33],
can effectively characterize the adhesive wear. However, these complicated models demand the determination of several variables, including the surface profile and its parameters. These factors make it very difficult for the practitioners to implement for estimating adhesive wear.
On the other hand, thermodynamic-based approaches[34][35][36] provide wear models that directly correlate the degradation of a tribo-pair due to wear with entropy flow. The wear model using DEG theorem is one such wear model developed using thermodynamic principles and is provided in Equation (3).

where μ is the friction coefficient and T is the contact temperature. Now, comparing Equations. (2) and (3) it can be concluded that the Archard equation is subsumed in the degradation−entropy relationship obtained from the DEG theorem. Therefore, it can be hypothesized that the degradation of the tribo-pairs can be effectively characterized using the DEG theorem. The equations for B and K for different sliding directions and operating conditions are provided in Table 1. Apart from these models, other adhesive wear equations employed to characterize the adhesive wear are presented in our recent work[37].
Table 1 Equations for B and K for different sliding directions and operating conditions
| Sl. no. | Sliding Direction | Operating condition | Deg. Coef. (B) | Wear Coef. (K) |
| 1 |  |
 |
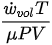 |
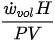 |
| 2 |  |
 |
 |
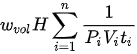 |
| 3 |  |
 |
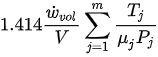 |
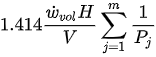 |
| 4 |  |
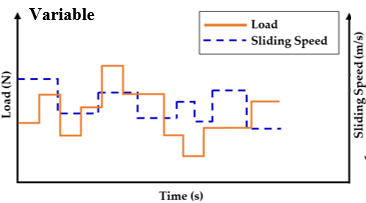 |
 |
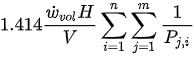 |
| 5 |  |
 |
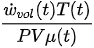 |
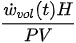 |
3. Efficacy of Degradation Coefficient B
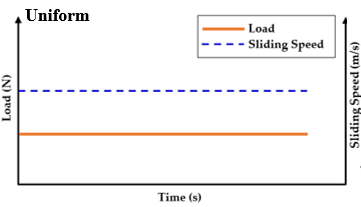
3.1 Uni-direction uniform operating conditions
Doelling et al[38] were the first to provide an explicit correlation between degradation and entropy generation for a tribo-system with experimental validation. Similarly, Brahmeshwarkar[39], experimentally verified the correlation between wear and entropy flow in bronze SAE 40 on steel 4140 and brass on steel 4140 tribo-pairs (see Figure 1).
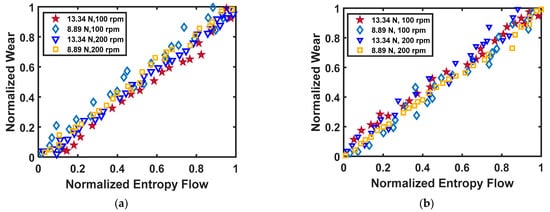
Bryant and Khonsari[40] were the first to experimentally validate the correlation between wear and entropy flow through B via Equation (3). Followed by their study, Lijesh and Khonsari[34] demonstrated the efficacy of the B over K by considering the experimental results from Aghdam and Khonsari[41] and Amiri et al[42]. The results are plotted in Figure 2.
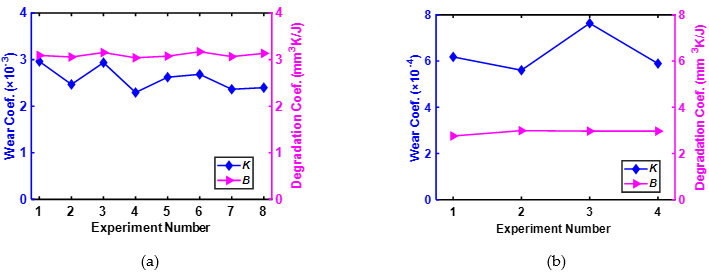
Figure 2 Comparing the variation of B and K values from [41] [123] and [42] [127] (a) using data from[41] (b) using data from[42]
3.2 Uni-direction variable operating conditions
Numerous engineering components in the industry are subjected to varying loads and/or operating speeds. As a result, these components often tend to degrade faster than uniform operating conditions[43][44][45]. The variations in operating conditions are responsible for significant damage and shorten the service life of bearings and gears[46][47].
Using the experimental results from Akbarzadeh and Khonsari[48], Lijesh and Khonsari[49] established the efficacy of the B over K, for the tribo-pair experiencing variable loading. The comparison of the measured and estimated wear values using B and K is provided in Figure 3. From this figure, it can be observed that the DEG theorem can reliably characterize the wear of tribo-pair experiencing variable loading.
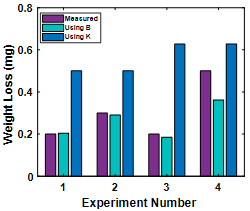 Figure 3. Comparison of weight loss between the measured and predicted weight loss using K and B from the data[49]
Figure 3. Comparison of weight loss between the measured and predicted weight loss using K and B from the data[49]
Lijesh and Khonsari[49] extended their study and demonstrated the efficacy of the B in characterizing the variable sliding speeds and arbitrary combination of both load and sliding speed.
3.3 Bi-direction sliding involving reciprocating/oscillatory motion
The results presented in Section 3.2 focused on uni-directional sliding motion. However, in practice, many machines—such as engines, pin-bushings in excavators, drag liners, etc.—experience either reciprocating or oscillatory motion that necessitates characterizing wear bi-directional sliding[50][51][52]. Research shows that applying the Archard equation to assess wear in such conditions does not yield satisfactory results. The reason is often attributed to factors such as the variation in friction force, wear mode, displacement amplitude, contact geometry, etc. In contrast, the degradation coefficient, which includes friction coefficient, temperature, wear, and operating conditions effectively characterizes the degradation in bi-directional motion.
The hypothesis is demonstrated using the experimental data from Rajeev et al.[53], and Aghdam and Khonsari[54]. The comparison of the measured and estimated wear values using the DEG theorem is provided in Figure 4. The results of Figure 4 suggest that wear values obtained using B can accurately predict the degradation of tribo-pair experiencing bi-directional sliding with the uniform sliding condition.
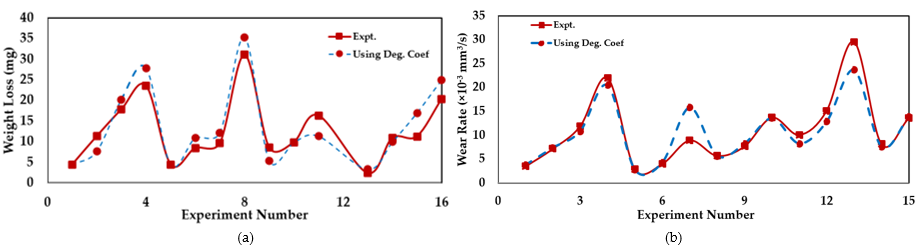
Figure 4. Comparison of weight loss obtained from experiment[53] and [54] using degradation coefficient. (a) wear data from [53] (b) wear data from [54]
3.4 Bi-directional variable operating conditions
As discussed in Section 3.2, compared to uniform operating conditions, the degradation of tribo-pair is more severe during a variable operating condition. Therefore, to evaluate the efficacy of B over K under variable operating conditions, Lijesh and Khonsari[55] performed experiments under bi-directional oscillating motion, and the values of wear rate determined from experiments using B and K are shown in Figure 5. From this figure, it is inferred that the wear loss measured from the experiment and determined using B is approximately the same; however, the values determined using K are observed to be constant irrespective of the operating conditions. It can thus be concluded that the wear of a tribo-pair experiencing variable operating conditions with bi-directional sliding motion can be accurately characterized through B.
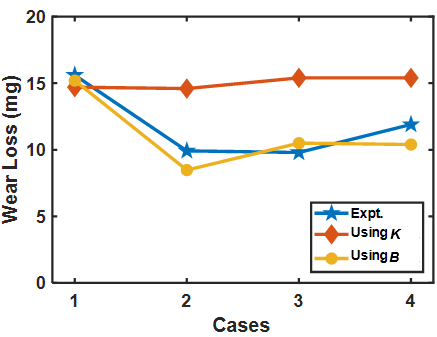
Figure 5. Comparison of wear loss from the experiment and determined using K and B [55]
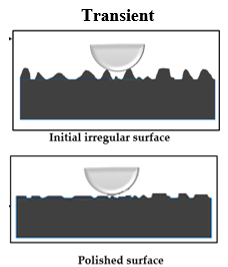
3.5 Transient wear
Using thermodynamic principles, Lijesh et al[34] proposed an analytical wear model to characterize the transient wear (see the Equations for B in Table 1). To prove the efficacy of the degradation coefficient compared to the wear coefficient, Lijesh et al[34] performed experiments on a vertically oriented pin-on-disk test setup. The results reveal that the transient wear predicted using the Archard coefficient deviated by ~27% compared to the degradation coefficient. The deviation was due to considering the time-dependent friction coefficient and contact temperature by the degradation coefficient.
The results of extensive tests suggest that the degradation coefficient can effectively characterize the degradation of tribo-pair involving uni-directional, bi-directional, transient operating conditions (e.g., during the running-in period), and variable loading/speed sequencing. However, research is needed to describe the path forward for analyzing more complex forms of wear involving multiple modes— e.g., combined adhesive and abrasive wear, mild to severe wear arising that leads to scuffing, galling, smearing, and seizing—and wear in boundary- and mixed-lubricated regimes
4. Conclusions
The capability of DEG theorem (developed according to the thermodynamic principles) in providing a unified wear model is discussed. The DEG theorem relates the degradation of the tribo-pair to the entropy generation through the degradation coefficient B. The study focused on tribo-pair degradation due to the adhesive wear prevalent in different directions of sliding motion (uni- and bi-directional), operating conditions (uniform and variable loading/speed), and transient wear. To establish the efficacy of B, the results of many recent reports were reviewed from the perspective of both theoretical and experimental validation. It is shown that the DEG theorem is able to correlate the degradation due to wear better than the Archard coefficient.
References
- H.C. Meng; K.C. Ludema; Wear models and predictive equations: their form and content. Wear 1995, 181-183, 443-457, 10.1016/0043-1648(95)90158-2.
- J. F. Archard; Contact and Rubbing of Flat Surfaces. Journal of Applied Physics 1953, 24, 981-988, 10.1063/1.1721448
- Deuis, R.L.; Subramanian, C.; Yellup, J.M. Dry sliding wear of aluminum composites—A review. Compos. Sci. Technol. 1997, 57, 415–435.
- Zhang, J.; Alpas, A.T. Transition between mild and severe wear in aluminum alloys. Acta Mater. 1997, 45, 513–528. [Google Scholar] [CrossRef]
- Giordano, M.; Schmid, S.; Arjmandi, M.; Ramezani, M. Abrasive wear of polymer fibers investigated by reciprocal scratching in an atomic force microscope. J. Tribol. 2018, 140, 021604.
- Godet, M. Modeling of Friction and Wear Phenomena. In Approaches to Modeling of Friction and Wear; Springer: New York, NY, USA, 1988; pp. 12–36.
- Ramesh, C.S.; Khan, A.A.; Ravikumar, N.; Savanprabhu, P. Prediction of wear coefficient of Al6061–TiO2 composites. Wear 2005, 259, 602–608.
- Fereidouni, H.; Akbarzadeh, S.; Khonsari, M. On the assessment of variable loading in adhesive wear. Tribol. Int. 2019, 129, 167–176
- Qureshi, F.; Sheikh, A. A probabilistic characterization of adhesive wear in metals. IEEE Trans. Reliab. 1997, 46, 38–44.
- Yang, L.J. Prediction of steady-state wear coefficients in adhesive wear. Tribol. Trans. 2004, 47, 335–340
- Quinn, T.F.J. Review of oxidational wear: Part I: The origins of oxidational wear. Tribol. Int. 1983, 16, 257–271.
- Osara, J.A.; Bryant, M.D. Performance and degradation characterization of electrochemical power sources using thermodynamics. Electrochim. Acta 2021, 365, 137337.
- Osara, J.A.; Bryant, M.D. Thermodynamics of grease degradation. Tribol. Int. 2019, 137, 433–445.
- Lijesh, K.P.; Khonsari, M.M. On the assessment of mechanical degradation of grease using entropy generation rate. Tribol. Lett. 2019, 67, 50.
- Zhou, Y.; Bosman, R.; Lugt, P.M. A model for shear degradation of lithium soap grease at ambient temperature. Tribol. Trans. 2018, 61, 61–70.
- Khonsari, M. M. and Amiri, M. Introduction to Thermodynamics of Mechaincal Fatigue, CRC, press, 2012.
- Lijesh, K.P.; Khonsari, M.M. Characterization of multiple wear mechanisms through entropy. Tribol. Int. 2020, 152, 106548
- Lijesh, K.P.; Khonsari, M.M. Characterization of abrasive wear using degradation coefficient. Wear 2020, 450, 203220.
- Stachowiak, G.W.; Batchelor, A.W. Engineering tribology. In Tribology Series, 24; Elsevier Science: Amesterdam, The Netherlands, 1993.
- Kragel’skiĭ, I.V. Friction and wear. In Butterworths; Oxford, Pergamon Press: Oxford, UK, 1965.
- Bryant, M.; Khonsari, M.; Ling, F. On the thermodynamics of degradation. Proc. R. Soc. A Math. Phys. Eng. Sci. 2008, 464, 2001–2014.
- Amiri, M.; Khonsari, M.M. On the Thermodynamics of Friction and Wear―A Review. Entropy 2010, 12, 1021–1049.
- Bryant, M.D. Unification of friction and wear. Recent Dev. Wear Prev. Frict. Lubr. 2010, 248, 159–196.
- Banjac, M.; Vencl, A.; Otović, S. Friction and wear processes—Thermodynamic approach. Tribol. Ind. 2014, 36, 341–347.
- Holm, R. Electric Contacts: Theory and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1946.
- Rabinowicz, E. The nature of the static and kinetic coefficients of friction. J. Appl. Phys. 1951, 22, 1373–1379.
- Yang, L.J. Prediction of steady-state wear coefficients in adhesive wear. Tribol. Trans. 2004, 47, 335–340.
- Welsh, N.C. The dry wear of steels I. The general pattern of behaviour. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1965, 257, 31–50.
- Vancoille, E.; Celis, J.; Roos, J. Dry sliding wear of TiN based ternary PVD coatings. Wear 1993, 165, 41–49.
- M.Z. Huq; J.-P. Celis; Expressing wear rate in sliding contacts based on dissipated energy. Wear 2002, 252, 375-383, 10.1016/s0043-1648(01)00867-5.
- Finkin, E.F. Speculations on the theory of adhesive wear. Wear 1972, 21, 103–114.
- Sahoo, P.; Chowdhury, S.R. A fractal analysis of adhesive wear at the contact between rough solids. Wear 2002, 253, 924–934.
- Nosonovsky, M.; Bhushan, B. Thermodynamics of surface degradation, self-organization and self-healing for biomimetic surfaces. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2009, 367, 1607–1627.
- Lijesh, K.P.; Khonsari, M.M.; Kailas, S.V. On the integrated degradation coefficient for adhesive wear: A thermody-namic approach. Wear 2018, 408, 138–150.
- Hansen, N.; Schreyer, H. A thermodynamically consistent framework for theories of elastoplasticity coupled with damage. Int. J. Solids Struct. 1994, 31, 359–389.
- Beheshti, A.; Khonsari, M.M. A thermodynamic approach for prediction of wear coefficient under unlubricated sliding condition. Tribol. Lett. 2010, 38, 347–354.
- Lijesh KP, and M. M. Khonsari. "A Unified Treatment of Tribo-Components Degradation Using Thermodynamics Framework: A Review on Adhesive Wear." Entropy 23, no. 10 (2021): 1329.
- Doelling, K.L.; Ling, F.F.; Bryant, M.D.; Heilman, B.P. An experimental study of the correlation between wear and entropy flow in machinery components. J. Appl. Phys. 2000, 88, 2999–3003.
- Brahmeshwarkar, S. A Thermodynamic Model for Wear in Sliding Contact. LSU. Master’s Thesis, Louisiana State University, Baton Rouge, Louisiana, 2006.
- Bryant, M.D.; Khonsari, M.M. Application of degradation-entropy generation theorem to dry sliding friction and wear. In Proceeding of the International Joint Tribology Conference, Miami, FL, USA, 20–22 October 2008; Volume 43369, pp. 1–3.
- Aghdam, A.; Khonsari, M. On the correlation between wear and entropy in dry sliding contact. Wear 2011, 270, 781–790.
- Amiri, M.; Khonsari, M.M.; Brahmeshwarkar, S. An application of dimensional analysis to entropy-wear relationship. J. Tribol. 2012, 134, 011604.
- Al-Tubi, I.; Long, H.; Tavner, P.; Shaw, B.; Zhang, J. Probabilistic analysis of gear flank micro-pitting risk in wind turbine gearbox using supervisory control and data acquisition data. IET Renew. Power Gener. 2015, 9, 610–617.
- Worden, K.; Sohn, H.; Farrar, C. Novelty detection in a changing environment: Regression and interpolation approaches. J. Sound Vib. 2002, 258, 741–761.
- McBain, J.; Timusk, M. Fault detection in variable speed machinery: Statistical parameterization. J. Sound Vib. 2009, 327, 623–646.
- LaCava, W.; Xing, Y.; Marks, C.; Guo, Y.; Moan, T. Three-dimensional bearing load share behaviour in the planetary stage of a wind turbine gearbox. IET Renew. Power Gener. 2013, 7, 359–369.
- Dong, W.; Xing, Y.; Moan, T.; Gao, Z. Time domain-based gear contact fatigue analysis of a wind turbine drivetrain under dynamic conditions. Int. J. Fatigue 2013, 48, 133–146.
- Akbarzadeh, S.; Khonsari, M.M. On the applicability of miner’s rule to adhesive wear. Tribol. Lett. 2016, 63, 1–10.
- Lijesh, K.P.; Khonsari, M.M. On the modeling of adhesive wear with consideration of loading sequence. Tribol. Lett. 2018, 66, 105.
- Huq, M.Z.; Celis, J.P. Reproducibility of friction and wear results in ball-on-disc unidirectional sliding tests of TiN-alumina pairings. Wear 1997, 212, 151–159.
- Mohtiichcr, H. The Tribological Perfmance of Advanced Hard Coatings under Fretting Conditions. Ph.D. Thesis, Kalholiekc Univcrsitcit Leuvcn, Leuven, Belgium, 1995.
- Blau, P.J.; Walukas, M. Sliding friction and wear of magnesium alloy AZ91D produced by two different methods. Tribol. Int. 2000, 33, 573–579.
- Rajeev, V.R.; Dwivedi, D.K.; Jain, S.C. Dry reciprocating wear of Al–Si–SiCp composites: A statistical analysis. Tribol. Int. 2010, 43, 1532–1541.
- Aghdam, A.B.; Khonsari, M.M. Prediction of Wear in Reciprocating Dry Sliding via Dissipated Energy and Temperature Rise. Tribol. Lett. 2013, 50, 365–378.
- Lijesh, K.P.; Khonsari, M.M. On the degradation of tribo-components undergoing oscillating sliding contact. Tribol. Int. 2019, 135, 18–28.




