
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Isaac Bersuker | + 1930 word(s) | 1930 | 2021-09-06 04:19:31 | | | |
| 2 | Isaac Bersuker | -2 word(s) | 1928 | 2021-10-25 17:54:13 | | | | |
| 3 | Camila Xu | -7 word(s) | 1921 | 2021-10-26 03:55:10 | | |
Video Upload Options
The fundamental property of a polyatomic system to undergo spontaneous symmetry breaking was first formulated by L. Landau in 1934 as follows: the configuration of any nonlinear polyatomic system in a degenerate electronic state undergoes spontaneous distortions that remove the degeneracy. This groundbreaking idea, appended with proof, was published by H. Jahn and E. Teller, resulting in what is presently known as the Jahn-Teller effect (JTE). Since then, many extensions of this groundbreaking idea were revealed and developed. Presently, four types of electronic structures that lead to spontaneous symmetry breaking are revealed: in addition to electronic degeneracy resulting in the proper Jahn-Teller effect, two or more close in energy (pseudodegenerate) electronic states may lead to similar instability and distortions, called the pseudo-JTE (PJTE), and the same spontaneous distortion effects may take place when there is neither degeneracy, nor pseudodegeneracy in the fground state of the high-symmetry configuration, but a strong JTE or pseudo-JTE take place in a low-lying excited state, that penetrates the ground state, distorting the system; these are the hidden -JTE and hidden-PJTE, respectively.
1. History and Extended Definitions
Since the first formulations of the JTE [1][2] the understanding of the origin of space configuration of polyatomic systems and their spontaneous distortions has undergone dramatic developments [3][4][5][6][7]. First, it was shown that the spontaneous distortion may take place also when the degenerate energy level is slightly split (pseudodegenerate) [8]. This result served as a trigger to a much more important conclusion that sufficiently strong vibronic coupling between any two electronic states (often ground and excited) with any energy gap between them may lead to instability and distortion of high-symmetry polyatomic configurations; this is the pseudo-JTE (PJTE) (see in [3][4][5][7][9]). More recently, it was shown that in the absence of electronic degeneracy and sufficient pseudodegeneracy in the ground state of a high-symmetry system (meaning no JTE or PJTE), there may be a strong JTE or PJTE in the low-lying excited electronic state that penetrate the high-symmetry ground state producing a distorted ground state configuration. These are the hidden-JTE (h-JTE) and hidden-PJTE (h-PJTE), respectively [10][11]. Fig. 1 illustrates these definitions of the four kind of JTE-type effects, jointly JT effects (JTEs) of instability and spontaneous distortions of high-symmetry configuration of polyatomic systems.
The general condition of JTEs is thus the presence of two or more electronic states that are strongly coupled by the nuclear displacements (vibronic coupling). This kind of strong vibronic coupling takes place when the electronic ground or low-lying excited states are degenerate or pseudodegenerate. The condition of the latter is Δ<F2/K0, where 2Δ is the energy gap between the interacting electronic states (for degenerate states Δ=0), F is the vibronic coupling constant, and K0 is the primary force constant (the stiffness of the system without the vibronic coupling). See Fig. 1 and Refs. [3][4][5] for more details in these definitions.
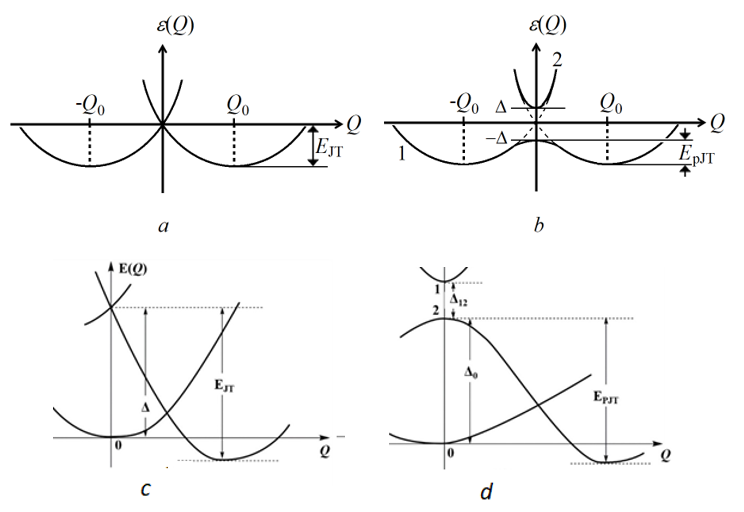
Figure 1. Illustration to the definition of the four types of electronic configurations causing the four kinds of Jahn-Teller effects; in all four cases Q is the symmetrized coordinate of the low-symmetry nuclear displacements from the reference high-symmetry configuration at Q=0, EJT is the JTE stabilization energy, and Δ denotes energy gaps; a) In the case of proper JTE the system is unstable, it has no minimum of the adiabatic potential energy surface (APES) at the point of electronic degeneracy Q=0, but it may be stable in the distorted configurations at ±Q0; b) The pseudo-JTE (PJTE) case: there is no degeneracy at Q=0, but the system is unstable (the curvature K of the ground-state APES is negative) due to the pseudodegeneracy caused by strong vibronic coupling F to low-lying excited states at Δ<F2/K0 (see the text); c) Hidden-JTE: there is neither degeneracy nor pseudodegeneracy in the ground state of the system, but there is a relatively low-lying excited state that has a JTE, which is so strong, EJT>Δ, that its penetrates the high-symmetry ground state, producing a global minimum with a distorted configuration; d) Hidden-PJTE: the same situation as in the hidden-JTE, but the intervening excited state has a strong PJTE instead of the JTE.
In terms of the first principles of quantum mechanics, the JTEs emerge as a violation of the adiabatic approximation in the separation of the electronic and nuclear motions, and serve as a correction to compensate for this violation [4]. In this sense, the role of the two or more electronic states in the occurrence of the JTEs is quite understandable, as their coupling increases the nonadiabaticity.
2. Uniqueness of the JTE origin of spontaneous symmetry breaking
With PJTE, h-JTE and h-PJTE added to the original JTE, we assume that there are no high-symmetry polyatomic configurations that can a priori be excluded from the possibility of spontaneous symmetry breaking. But a more important conclusion emerged when it was proved that the JTE and the PJTE are the only source of instability and spontaneous distortions of high-symmetry configurations of polyatomic systems (see in [4][5] and references therein). The four cases of electronic structure that lead to JTEs, shown in Figure 1, are thus the only possible causes of spontaneous symmetry breaking of high-symmetry configurations. Moreover, it was shown that degeneracy and pseudodegeneracy are the only source of SSB in the whole spectrum of transformations in matter from elementary particles to nuclei, to atoms, molecules and solids [12]. It follows like “Nature trends to avoid degeneracies and pseudodegeneracies in the atomic world by means of symmetry breaking”.
The uniqueness of the JTEs as the only source of instability and spontaneous symmetry breaking in atomic systems was proved by showing that when only the nondegenerate ground electronic state of the high-symmetry configuration is taken into account in determining the force constant with respect to low-symmetry distortions, its value is positive, K0>0 (always!), meaning the configuration is stable, but the contribution Kv of the other electronic states that are in vibronic coupling to the ground state, which is always negative, Kv<0, may lead to instability, K= K0 + Kv <0 [4][5].
3. Driving forces, dynamic distortions, and improved definition of polyatomic space configurations
In atomic systems, all the spontaneous symmetry breakings are controlled by chemical bonding, electrostatic and/or covalent. In the case of the JTE in high-symmetry configurations induced by electronic degenerate states the charge distribution in each of them has necessarily lower symmetry then that of the system (with the same symmetry, the two or more degenerate electronic states will not be mutually orthogonal), thus distorting the nuclear framework. In the PJTE cases, the distorting forces are of covalent origin. Fig. 2 illustrates the origin PJTE-driven out-of-plane displacement of the iron atom of the porphyrin ring in hemoglobin as due to the added covalence bonding to the ring by this displacement.
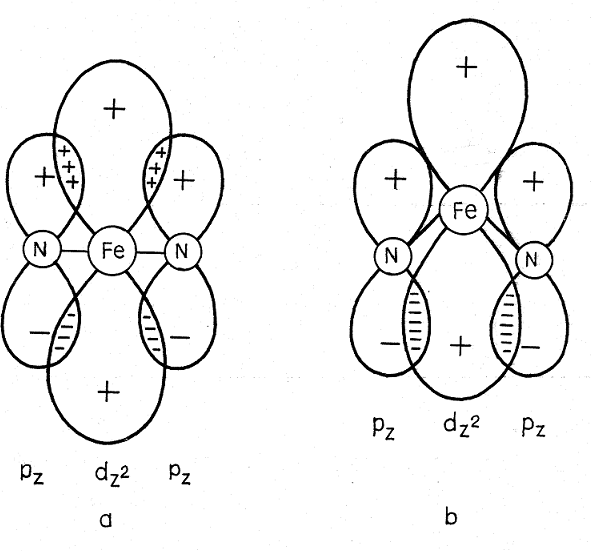
Figure 2. Illustration to the origin of the pseudo Jahn-Teller effect using the N--Fe--N fragment of the square-planar FeN4 group of iron porphyrin in hemoglobin as an example [13]: (a) when Fe is in the N4 plane (on the N-Fe-N line), the dπ-pπ overlap between the HOMO (nitrogen pπ) and LUMO (iron dz2) orbitals is zero (positive and negative overlaps compensate each other); (b) the out-of-plane displacement of the Fe atom results in nonzero dπ-pπ overlap and covalent bond formation, which lowers the curvature of the adiabatic potential in the direction of such displacements.
Another important feature of the JTEs distortions is their dynamic nature. The starting high-symmetry configuration of the system means that there are two or more equivalent directions of distortions. Accordingly, the JTEs-induced APES have two or more equivalent minima, which together, in the absence of external perturbations (including measurements), do not violate the reference symmetry. However, the multiminimum APES leads to the dynamic nature of the JTEs spontaneous distortions with tunneling or over-the barrier transitions between them, resulting in a series of novel effects with dramatic influence of the observable properties (see [3][4][5][6][7][9] and Section 5 below).
In a general view, the four kinds of the JTEs, briefly outlined above, show that there are no polyatomic configurations, which can be a priori excluded from the possible local instability and spontaneous distortions, with all the consequent influence on observable properties. In this respect, it was suggested [7] to separate all the polyatomic systems in three groups with respect to the possible influence of the JTEs-induced spontaneous symmetry breaking. In the first group, polyatomic systems are stable in the high-symmetry configuration (meaning no degeneracy, pseudodegeneracy, or low-lying electronic states with degeneracy or pseudodegeneracy). From the theoretical point of view, these are systems with very low nonadiabaticity in the high-symmetry configuration. This group contains the huge variety of chemical compounds the chemists are working with (but far not all of them).
The second group contains the systems with moderate to strong (but not very strong) nonadiabaticity, induced by the presence of electronic degeneracy or pseudodegeneracy (one of the four kinds illustrated in Figure 1). These are systems with special properties and massive applications, partially mentioned in this text.
The third group are systems with very strong JTEs (strong nonadiabaticity in the high-symmetry configuration) and related strong distortions from the high-symmetry configuration (e.g., the water molecule, which is unstable in the high-symmetry linear configuration due to the strong PJTE). These systems, once synthesized, fall in one of the low-symmetry minima of the APES and remain there forever (no tunneling or over-the-barrier transition between the minima are possible because of the very high barriers).
4. Specifics in experimental observation of JTEs
In view of the multiminimum APES and the consequent dynamic nature of the JTEs, the direct observation of the latter is not straightforward. As the problem is in observation of symmetry breaking, it is appropriate to invoke the P. Curie principle [14], according to which experimental observation of symmetry elements in physical or chemical phenomena is limited, in the sense that low-symmetry elements of the phenomenon may not show up in the observation with a given method (see more details in Refs. [7][12][15]. In terms of the JTEs problems, the lifetime τ of the system in the distorted configuration in the minimum of the multiminimum APES may be too short to be observed by the “time of measurement” τ' (e.g., the period of the electromagnetic wave), thus showing an averaged undistorted picture instead of JTEs distorted one. This means that the latter can be observed by the methods with short τ' values, or when the dynamics is quenched by external perturbations, but they may not be seen by methods with larger τ'. The JTEs in systems with small τ values were ignored for a long time (as unobservable, negligible), but they got a new life recently in view of important applications (see next section).
5. Recent extended reviews and important applications
In addition to the known books and reviews devoted to the JTEs (see, e.g., [3][4][5][6] and references to books in [7]), there are more newly published important further developments. For a general view on recent achievements in the JTEs theory and applications see reviews [7][9][15][16][17][18][19][20] and the (not less important) references therein. References to the computational aspects of the vibronic coupling theory underlying the JTEs are given in the reviews [7][20]. A variety of perovskite crystal properties controlled by the PJTE, including the origin of ferroelectricity, multiferroicity, flexoelectricity, orientational polarization, and relaxor properties, is elucidated in Refs. [15][16]. Manipulation of crystal lattices by means of redox influence of vulnerable JTE centers is illustrated in Ref. [17]. Other specific applications in materials science including manipulation of structure and properties of two-dimensional systems by means of external influence targeting the PJTE parameters are developed in [18][19]. The rapidly increasing applications of the JTEs in the search of qubits for quantum information devices is demonstrated by Ref. [21].
References
- Teller, E. An Historical Note. In Englman, R. The Jahn-Teller Effect in Molecules and Crystals; Wiley: London, 1972, Foreword.
- Jahn, H. A.; Teller, E. Instability of polyatomic molecules in degenerate electronic states. I. Orbital degeneracy. Proc. Roy. Soc. London A 1937, 161, 220-235.
- Englman, R. The Jahn-Teller Effect in Molecules and Crystals; Wiley: London, 1972.
- Bersuker, I. B.; Polinger, V. Z. Vibronic interactions in Molecules and Crystals. Springer-Verlag: Berlin-Heidelberg, 1989.
- Bersuker, I. B. The Jahn-Teller Effect; Cambridge University Press: Cambridge, UK, 2006.
- Köppel, M.; Domcke, W.; Cederbaum, L. S. Multimode molecular dynamics beyond the Born-Oppenheimer approximation. Adv. Chem. Phys. 1984, 57, 59-246.
- Bersuker I. B., Jahn–Teller and Pseudo-Jahn–Teller Effects: From Particular Features to General Tools in Exploring Molecular and Solid State Properties. Chem. Rev. 2021, 121, 3, 1463-1512; https://dx.doi.org/10.1021/acs.chemrev.0c00718.
- Öpik, U. and Pryce, M. H. L. Studies of the Jahn-Teller effect I. A survey of the static problem. Proc. R. Soc. London 1957, A 238, 425-447.
- Bersuker, I. B. The Pseudo Jahn-Teller Effect – a Two-State Paradigm in Formation, Deformation, and Transformation of Molecular Systems and Solids. Chem. Rev. 2013, 113, 1351-1390.
- Bersuker, I. B., Recent Developments in the Jahn-Teller Effect theory. The Hidden Jahn-Teller Effect. In The Jahn-Teller effect. Fundamentals and Implications for Physics and Chemistry, Köppel, H., Yarkony, D.R., Barentzen, H., Eds.; Springer Series of Chemical Physics, Springer: Heidelberg, 2009, Vol. 97, Chapter 1, pp 3-23.
- Bersuker, I. B. Hidden Jahn-Teller and Pseudo-Jahn-Teller effects, Encyclopedia, 2020, General & Theoretical Physics, Topic Review; https://encyclopedia.pub/4283
- Bersuker, I. B. Spontaneous Symmetry Breaking in Matter Induced by Degeneracy and Pseudodegeneracy. In Advances in Chemical Physics, Rice, S., Dinner, R. Eds.; Wiley: New York, 2016; Vol. 160, pp159-208.
- Bersuker, I. B.; Stavrov, S. S. Structure and properties of metalloporphyrins and hemoproteins: the vibronic approach, Coord. Chem. Revs, 88, 1-68 (1988).
- Curie, P. Sur la symmetrie dans les phenomene physiques: symmetrie d’un champ electriques et d’un champ magnetique. Journal de Physique, 1894, 3, 393-415.
- Bersuker, I. B. The Vibronic (Pseudo Jahn-Teller) Theory of Ferroelectricity. Novel Aspects and Applications, Ferroelectrics, 2018, 536, 1-59 ; https://doi.org/10.1080/00150193.2018.1528919
- Bersuker, Isaac B.; Polinger, Victor. Perovskite Crystals: Unique Pseudo-Jahn–Teller Origin of Ferroelectricity, Multiferroicity, Permittivity, Flexoelectricity, and Polar Nanoregions, Condens. Matter 2020, 5, 68; https://doi.org/10.3390/condmat5040068
- Gudkov, V.V., Sarychev, M.N., Zherlitsyn, S., Zhevstovskikh, I. V., Averkiev, N. S., Vinnik, D. A., Gudkova, S. A., Niewa, R. , Dressel, M., Alyabyeva, L. N., Gorshunov, B. P., and Bersuker, I. B. Sub-lattice of Jahn-Teller centers in hexaferrite crystal. Sci. Rep. 2020, 10, 7076-7091; https://doi.org/10.1038/s41598-020-63915-7.
- Bersuker, Isaac B. Manipulation of structure and properties of two-dimensional systems employing the pseudo Jahn-Teller effect. FlatChem 2017, 6, 11-27.
- Gorinchoy, N. N. and I. B. Bersuker, Origin of Puckering (Buckling) of Planar Heterocycles and Methods of Its Suppression, in Heterocycles: synthesis, reactions and applications, Ed. Jonas M. Danielsen, Nova Science Publishers, 2020, pp 129-188.
- Sharma, Ketan, Miller, Terry A., and Stanton, J. F. Vibronically coupled states: computational considerations and characterization of vibronic and rovibronic spectroscopic parameters, International Reviews in Physical Chemistry, 2021, 40, 165-298.
- Thiering, Gergő; Gali, Adam. The (eg⊗eu)⊗Eg product Jahn–Teller effect in the neutral group-IV vacancy quantum bits in diamond. Nature Computational Materials, 2019, 5, 1-6.




