
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Houizot Patrick | + 1518 word(s) | 1518 | 2021-07-26 04:21:14 | | | |
| 2 | Bruce Ren | Meta information modification | 1518 | 2021-08-16 10:53:45 | | |
Video Upload Options
Stress corrosion cracking is a well-known phenomenon in oxide glasses. However, how amorphous phase separation (APS) alters stress corrosion cracking, and the overall mechanical response of an oxide glass is less known in literature. APS is a dominant feature concerning many multicomponent systems, particularly the ternary sodium borosilicate (SBN) glass systems.
1. Introduction
Since Before the Common Era, humankind has been fabricating oxide glasses for various uses. Over the years, interest in oxide glasses has grown due to advantageous optical, chemical, and electrical properties [1]. Some of these properties include optical transparency, electrical isolation, and a high melting point (between 800–1800 °C depending on the chemical composition). Yet oxide glasses have a major drawback: they seem to fail abruptly. However, studying the failure of the glass samples in detail frequently leads one to discover sub-critical crack growth, also called stress corrosion cracking (SCC) because it is aided by environmental factors, or flaws that occurred before the dynamic fracture. For homogenous oxide glasses, this phenomenon is well documented in literature [2][3][4][5][6][7][8][9][10][11]. Moreover, the SCC properties are known to depend on the chemical composition of the oxide glass [2][3][4], the fictive temperature [5][6], the environmental factors [7][8][9][10][11], etc. In recent years, it has become apparent that understanding dynamic and sub-critical cracking requires a detailed knowledge of how short- and medium-range structures influence physical and mechanical properties in these glasses. By gaining this deep understanding, researchers will obtain key knowledge to advancing glass technology. This will ultimately benefit all kinds of industry, including high technology fields such as laser technology, energy-saving technology, and communication technology.
A single-phase material has a structurally and chemically homogeneous distribution of its constituents. Multiphase materials occur when precipitates with structural and/or chemical composition differences form. Each phase in these materials is homogeneous, and there is a distinctive barrier between different phases [12][13][14]. Liquid–liquid phase separation occurs in multi-component liquids when the Gibbs energy curve shows two distinct minimums as a function of the liquid composition.
From a thermodynamic viewpoint, a simple binary system composed of components A and B can exist as a homogenous mixture (attractive interactions A–B), or it might prefer to exist as a heterogeneous mixture with repulsive A–B interactions. The preference to exist as a heterogeneous mixture induces phase separation over a well-defined range of compositions, temperatures, and pressures. Likewise, phase separation can also be due to irradiation [15]. Phase separation processes produce a large variety of mesoscopic structures, which modify the macroscopic behavior of the material. Theories propose different mechanisms to explain these scenarios taking into consideration the composition of the glass and the kinetic limits [16][17].
Over the years, researchers identified metastable miscibility gaps in multiple different types of oxide glass systems [18][19][20], particularly those based on silica and boron oxides [21][22][23]. Simulation and experimental approaches aid in obtaining phase diagrams to predict the miscibility gaps. These studies [24][25][26][27][28][29] help in understanding from short- to medium-range (micro and meso) structures of the glasses. Researchers also study how these changes scale up to variations in the overall physical and mechanical/fracture properties of phase separated glass systems [30][31]. An industrial application of phase separated glasses and their enhanced mechanical/fracture properties concerns crush-resistant glasses [32]. Furthermore, phase diagrams have industrial significance when considering functional materials, such as glass-ceramics and porous glasses [33][34][35].
2. Thermodynamic Interpretations of Phase Separation
Thermodynamic theories are some of the most widely accepted methods for explaining the occurrence of phase separation in materials. Section 3.1 reviews the case of a two-atom theoretical system. Section 3.2 turns to the more complex problem of multi-oxide glass systems. Section 3.3 addresses the special case of SiO 2- B 2O 3- Na 2O glasses. APS in glasses is usually considered and analyzed as liquid–liquid phase separation [17][36][37]. However, it should be noted that a glass is not in thermodynamic equilibrium; hence, discussions herein concern inherently metastable glasses.
Figure 1 depicts a typical miscibility gap and the Gibbs free energy curves as a function of x B . In Figure 1 a, the solid dark blue line represents the binodal curve, which is the boundary between the domain where only a single phase exists to a domain where multiple phases exist, and hence a miscibility gap. This curve is obtained from the shape variation of Gibbs free energy curves ( Figure 1 b,c).
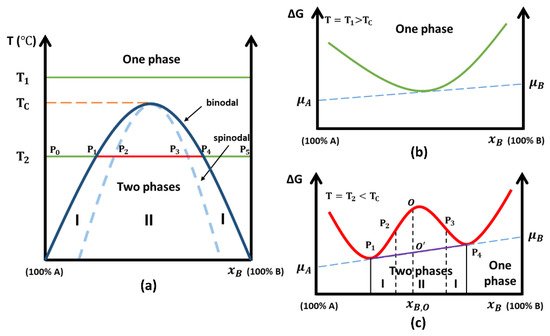
For many years, the CALPHAD (CALculation of PHAse Diagrams) method was used to provide predictions of liquid phase miscibility gaps in multiple different systems [40][41]. This method uses the Gibbs energy to calculate phase diagrams and thermodynamic properties. Input parameters include conditions such as chemical composition, temperature, and pressure. Extending CALPHAD methods to oxide glasses may give reliable estimates of the phase diagram [42], yet this is proving difficult because glass is not at equilibrium.
Generally, the ternary metastable liquid–liquid phase diagram is highly important. Moreover, kinetic factors also have essential effects on the phase separation processes. For a given glass with a chemical composition within the miscibility gap, annealing protocols determine: (1) the phase composition while attaining equilibrium ( Section 3.1 ), (2) the type of phase separation (binodal or spinodal) [43], (3) the nucleation/growth kinetics in the miscibility gaps [37][44], and (4) the final phase compositions and phase size [45][46][47]. The next section focuses on different structures of some APS-SBN (amorphous phase separated SBN) glasses.
3. Physical Properties of APS Glasses
The inherent structure of the glass and its amorphous phase separated counterpart could play a role in altering physical and mechanical/fracture glass properties. In this section, we take a closer look at how the APS structure of the glasses plays on the physical properties where Section 6 concentrates on the mechanical/fracture properties.
APS produces a large variety of structures in glasses. This affects the density calculations. Burnett and Douglas’ [37] investigations found that phase separation consists of two distinctive stages: (i) the decomposition stage when the developing phases gradually reaches the equilibrium composition; and (ii) the coarsening stage when the size of the phase separation regions increases without considerable changes in phase composition. At the end of the first stage, the dimension of phase separated regions are usually large enough to neglect the interfacial effects between different phases [48]. In this case, a two-phase glass can be considered as a composite material consisting of two different homogeneous substances, i.e., the tie-line end members .
From the above equations, the sign of the first derivative does not change with w B , and it depends on the quantitative comparison between ρ α and ρ β . Additionally, the second derivative is always positive. This shows that the curve of ρ as a function of one component’s initial weight fraction is convex.
The comparison between experiments and theory shows the wide usability of Equations (16) and (17). This analysis is also valid for ternary and higher-order systems in a two-phase region. In these regions, the above equations are valid if one follows the tie line of constant temperature [49][50].
4. Mechanical/Fracture Properties of APS Glasses
Glass is one of the most common materials in daily life due to many advantageous properties, including transparency, thermal and chemical stability, etc. However, its biggest disadvantage is its brittleness, which limits its uses in many applications. This is still the case despite a long history of developments aiming at overcoming this drawback [51][52][53][54]. To understand the mechanical/fracture properties of APS glasses, Section 6.1 first takes a closer look at the Young’s modulus of APS glasses. It highlights the PbO - B 2O 3 glass systems discussed in Section 5 . Then, Section 6.2 addresses some fracture properties of APS glasses, including the interaction between the crack front and secondary phases during dynamic fracture ( Section 6.2.1 ), fracture toughness ( Section 6.2.2 ), sub-critical cracking ( Section 6.2.3 ) and post-mortem fracture surface analysis ( Section 6.2.4 ).
Likewise, Miyata et al. [55] studied B 2O 3-rich particles in a PbO -rich matrix (i.e., α m < α p , Γ m < Γ p , and E m > E p ). With all the theoretical analysis above, they proposed that the crack passes around the particles in this system.
As stated above, APS in glasses alters crack propagation at the mesoscale. Hence, macroscopic fracture properties should be influenced by these medium-range structural variations [56]. It has been widely considered that the presence of APS systematically increases the fracture toughness of the glass [57][58]. Several toughening mechanisms have been proposed to explain how heterogeneous inclusions affect the fracture behavior as it is mentioned at the beginning of Section 6.2.1 (crack pinning, deflection, trapping, etc.).
As was analyzed in Section 6.2.1 [55], for the PbO -rich particles/ B 2O 3-rich matrix where α m > α p , Γ m > Γ p , and E m < E p , the crack propagates preferentially through the PbO -rich phase; for the B 2O 3-rich particles/ PbO -rich matrix where α m < α p , Γ m < Γ p , and E m > E p , the crack propagates preferentially around the B 2O 3-rich “impenetrable” particles.
References
- Charleston, R.J.; Fisher, J.E.; Michael, J. Masterpieces of Glass: A World History from the Corning Museum of Glass; HN Abrams: New York, NY, USA, 1990; ISBN 0810924641.
- Barlet, M. Evolution of Mechanical Properties of Silicate Glasses: Impact of the Chemical Composition and Effects of Irradiation. Ph.D. Thesis, École Polytechnique, Palaiseau, France, 2014.
- Barlet, M.; Delaye, J.-M.; Boizot, B.; Caraballo, R.; Peuget, S.; Rountree, C.L. From network polymerization to stress corrosion cracking in sodium-borosilicate glasses: Effect of the chemical composition. J. Non-Cryst. Solids 2016, 450, 174–184.
- Rountree, C.L. Recent progress to understand stress corrosion cracking in sodium borosilicate glasses: Linking the chemical composition to structural, physical and fracture properties. J. Phys. D Appl. Phys. 2017, 50, 343002.
- Koike, A.; Tomozawa, M.; Ito, S. Sub-critical crack growth rate of soda-lime-silicate glass and less brittle glass as a function of fictive temperature. J. Non-Cryst. Solids 2007, 353, 2675–2680.
- Koike, A.; Tomozawa, M. Fictive temperature dependence of subcritical crack growth rate of normal glass and anomalous glass. J. Non-Cryst. Solids 2006, 352, 5522–5530.
- Ciccotti, M. Stress-corrosion mechanisms in silicate glasses. J. Phys. D Appl. Phys. 2009, 42, 214006.
- Wiederhorn, S.M. Influence of water vapor on crack propagation in soda-lime glass. J. Am. Ceram. Soc. 1967, 50, 407–414.
- Wiederhorn, S.M.; Freiman, S.W.; Fuller, E.R.; Simmons, C.J. Effects of water and other dielectrics on crack-growth. J. Mater. Sci. 1982, 17, 3460–3478.
- Wiederhorn, S.M.; Johnson, H.; Diness, A.M.; Heuer, A.H. Fracture of glass in vacuum. J. Am. Ceram. Soc. 1974, 57, 336–341.
- Célarié, F. Dynamique de Fissuration a Basse Vitesse des Matériaux Vitreux. Ph.D. Thesis, Université Montpellier II-Sciences et Techniques du Languedoc, Montpellier, France, 2004.
- Bernstein, J. Polymorphism in Molecular Crystals 2e; International Union of Crystal: Chester, England, 2020; Volume 30, ISBN 9780199655441.
- Findlay, A. The Phase Rule and Its Applications; Longmans, Green: Harlow, UK, 1904.
- Glasstone, S. Text-Book of Physical Chemistry; Van Nostrand Co.: New York, NY, USA, 1940.
- Möbus, G.; Ojovan, M.; Cook, S.; Tsai, J.; Yang, G. Nano-scale quasi-melting of alkali-borosilicate glasses under electron irradiation. J. Nucl. Mater. 2010, 396, 264–271.
- Cahn, J.W. Phase separation by spinodal decomposition in isotropic systems. J. Chem. Phys. 1965, 42, 93–99.
- James, P.F. Liquid-phase separation in glass-forming systems. J. Mater. Sci. 1975, 10, 1802–1825.
- Charles, R.J. Metastable immiscibility in BaO-Li2O-SiO2 system. Phys. Chem. Glasses 1967, 8, 185.
- Kim, S.S.; Sanders, T.H., Jr. Thermodynamic modeling of phase diagrams in binary alkali silicate systems. J. Am. Ceram. Soc. 1991, 74, 1833–1840.
- Mazurin, O.V.; Porai-Koshits, E.A. Phase Separation in Glass; Elsevier: Amsterdam, The Netherlands, 1984; ISBN 9780080983653.
- Ghanbari-Ahari, K.; Cameron, A.M. Phase diagram of Na2O-B2O3-SiO2 system. J. Am. Ceram. Soc. 1993, 76, 2017–2022.
- Kim, S.S.; Sanders, T.H., Jr. Calculation of subliquidus miscibility gaps in the Li2O-B2O3-SiO2 system. Ceram. Int. 2000, 26, 769–778.
- Polyakova, I.G. Alkali borosilicate systems: Phase diagrams and properties of glasses. Phys. Chem. Glasses 2000, 41, 247–258.
- Bouttes, D. Micro-Tomographie d’un Borosilicate de Baryum Démixé: Du Mûrissement à la Fragmentation. Ph.D. Thesis, ParisTech, Paris, France, 2014.
- Bouttes, D.; Gouillart, E.; Boller, E.; Dalmas, D.; Vandembroucq, D. Fragmentation and limits to dynamical scaling in viscous coarsening: An interrupted in situ X-ray tomographic study. Phys. Rev. Lett. 2014, 112, 245701.
- Bouttes, D.; Lambert, O.; Claireaux, C.; Woelffel, W.; Dalmas, D.; Gouillart, E.; Lhuissier, P.; Salvo, L.; Boller, E.; Vandembroucq, D. Hydrodynamic coarsening in phase-separated silicate melts. Acta Mater. 2015, 92, 233–242.
- Bouttes, D.; Gouillart, E.; Vandembroucq, D. Topological symmetry breaking in viscous coarsening. Phys. Rev. Lett. 2016, 117, 145702.
- Mazurin, O.V.; Roskova, G.P.; Kluyev, V.P. Properties of phase-separated soda-silica glasses as a means of investigation of their structure. Discuss. Faraday Soc. 1970, 50, 191–199.
- Oliveira, J.M.; Correia, R.N.; Fernandes, M.H. Effect of SiO2 on amorphous phase separation of CaO-P2O5-SiO2-MgO glasses. J. Non-Cryst. Solids 2000, 273, 59–63.
- Gueguen, Y.; Houizot, P.; Célarié, F.; Chen, M.; Hirata, A.; Tan, Y.; Allix, M.; Chenu, S.; Roux-Langlois, C.; Rouxel, T. Structure and viscosity of phase-separated BaO-SiO2 glasses. J. Am. Ceram. Soc. 2017, 100, 1982–1993.
- Pye, L.D.; Ploetz, L.; Manfredo, L. Physical properties of phase separated soda-silica glasses. J. Non-Cryst. Solids 1974, 14, 310–321.
- Hammel, J.; Allersma, T. Method of Making Thermally Stable and Crush Resistant Microporous Glass Catalyst Supports. U.S. Patent 3843341A, 22 October 1974.
- Enke, D.; Janowski, F.; Schwieger, W. Porous glasses in the 21st century—A short review. Microporous Mesoporous Mater. 2003, 60, 19–30.
- Ramsden, A.H.; James, P.F. The effects of amorphous phase separation on crystal nucleation kinetics in BaO-SiO2 glasses. J. Mater. Sci. 1984, 19, 1406–1419.
- Suzuki, M.; Tanaka, T. Materials design for the fabrication of porous glass using phase separation in multi-component borosilicate glass. ISIJ Int. 2008, 48, 1524–1532.
- Tomozawa, M. Liquid-phase separation and crystal nucleation in Li2O-SiO2 glasses. Phys. Chem. Glasses 1972, 13, 161.
- Burnett, D.G.; Douglas, R.W. Liquid-liquid phase separation in soda-lime-silica system. Phys. Chem. Glasses 1970, 11, 125.
- Campbell, F.C. Phase Diagrams: Understanding the Basics; ASM International: Almere, The Netherlands, 2012; ISBN 9781615039869.
- Varshneya, A.K. Fundamentals of Inorganic Glasses; Elsevier: Amsterdam, The Netherlands, 2013; ISBN 9780128162262.
- Bormann, R.; Gärtner, F.; Zöltzer, K. Application of the CALPHAD method for the prediction of amorphous phase formation. J. Less Common Met. 1988, 145, 19–29.
- Gossé, S.; Guéneau, C.; Bordier, S.; Schuller, S.; Laplace, A.; Rogez, J. A thermodynamic approach to predict the metallic and oxide phases precipitations in nuclear waste glass melts. Procedia Mater. Sci. 2014, 7, 79–86, ISSN 2211-8128.
- Benigni, P. CALPHAD modeling of the glass transition for a pure substance, coupling thermodynamics and relaxation kinetics. Calphad 2021, 72, 102238.
- Haller, W.; BlackBurn, D.H.; Wagstaff, F.E.; Charles, R.J. Metastable immiscibility surface in the system Na2O-B2O3-SiO2. J. Am. Ceram. Soc. 1970, 53, 34–39.
- Hammel, J.J. Direct measurements of homogeneous nucleation rates in a glass-forming system. J. Chem. Phys. 1967, 46, 2234–2244.
- Häßler, J.; Rüssel, C. Self-organized growth of sodium borate-rich droplets in a phase-separated sodium borosilicate glass. Int. J. Appl. Glass Sci. 2017, 8, 124–131.
- Brequel, H.; Parmentier, J.; Sorar, G.D.; Schiffini, L.; Enzo, S. Study of the phase separation in amorphous silicon oxycarbide glasses under heat treatment. Nanostruct. Mater. 1999, 11, 721–731.
- Wheaton, B.R.; Clare, A.G. Evaluation of phase separation in glasses with the use of atomic force microscopy. J. Non-Cryst. Solids 2007, 353, 4767–4778.
- Mazurin, O.V. Physical properties of phase separated glasses. J. Non-Cryst. Solids 1987, 95, 71–82.
- Shaw, R.R.; Breedis, J.F. Secondary phase separation in lead borate glasses. J. Am. Ceram. Soc. 1972, 55, 422–425.
- Shaw, R.R.; Uhlmann, D.R. Effect of phase separation on the properties of simple glasses. II. Elastic properties. J. Non-Cryst. Solids 1971, 5, 237–263.
- Hood, H.P.; Stookey, S.D. Method of Making a Glass Article of High Mechanical Strength and Article Made Thereby. U.S. Patent 2779136A, 29 January 1957.
- Mirkhalaf, M.; Dastjerdi, A.K.; Barthelat, F. Overcoming the brittleness of glass through bio-inspiration and micro-architecture. Nat. Commun. 2014, 5, 3166.
- Sehgal, J.; Ito, S. A new low-brittleness glass in the soda-lime-silica glass family. J. Am. Ceram. Soc. 1998, 81, 2485–2488.
- Wondraczek, L.; Mauro, J.C.; Eckert, J.; Kühn, U.; Horbach, J.; Deubener, J.; Rouxel, T. Towards ultrastrong glasses. Adv. Mater. 2011, 23, 4578–4586.
- Miyata, N.; Jinno, H. Strength and fracture surface energy of phase-separated glasses. J. Mater. Sci. 1981, 16, 2205–2217.
- Mecholsky, J.J. Toughening in glass ceramic through microstructural design. Fract. Mech. Ceram. 1983, 6, 165.
- Miyata, N.; Jinno, H. Use of Vickers indentation method for evaluation of fracture toughness of phase-separated glasses. J. Non-Cryst. Solids 1980, 38, 391–396.
- Seal, A.K.; Chakraborti, P.; Roy, N.R.; Mukerjee, S.; Mitra, M.K.; Das, G.C. Effect of phase separation on the fracture toughness of SiO2-B2O3-Na2O glass. Bull. Mater. Sci. 2005, 28, 457–460.




