1000/1000
Hot
Most Recent

The exchange bias (EB) is an effect occurring in coupled ferromagnetic/antiferromagnetic materials of diverse shapes, from core–shell nanoparticles to stacked nanostructures and thin films.
After its discovery in 1956, using Co/CoO core–shell particles [1], the exchange bias (EB) effect has been investigated in detail by many research groups. Typically, it occurs when a ferromagnet (FM) and an antiferromagnet (AFM) are in contact, and the system is cooled from high temperatures through the Néel temperature (the magnetic ordering temperature) of the AFM in an external magnetic field. In a naïve concept, this process freezes the AFM spins, in this way adding an “internal” magnetic field to the external one which leads to a horizontal shift of the FM hysteresis loop. However, other correlated phenomena, such as a vertical shift of the loop and an often occurring asymmetry of the hysteresis loop [2], cannot be explained by this most simple model.
While first studies concentrated on relatively simple FM/AFM combinations, such as the aforementioned Co/CoO [3][4], Fe/FeF2 [5][6], or Fe/MnF2 [7][8], which already exhibited quite interesting effects for the different materials, nowadays more complicated materials are under investigations, such as Fe/LaAlO3 [9] or Pr0.67Sr0.33MnO3/SrTiO3 [10], and more sophisticated structures, such as nanostructures [11][12][13] or multi-layer sandwiches [14][15].
Still, at the same time, new models are being developed to understand the exchange bias effect, which is already intensively used in magnetic data storage, qualitatively and quantitatively for all these different material combinations and structures.
Here, we give an update of recent experimental and theoretical research in the area of exchange bias. To avoid the additional impact of an in-plane component of the shape anisotropy in nanostructured or nanoparticle systems, we concentrate in this review on thin film samples, where the shape anisotropy often results in the magnetic moments being oriented in-plane.
Explaining all the aforementioned phenomena qualitatively and quantitatively by a model is obviously difficult, especially as different effects are found in different material systems or even in identical material systems, prepared in different ways. This is why after the first intuitive models, several other emerged, aiming at explaining as many experimentally observed effects as possible in a physically reasonable way. Naturally, with new experimental findings, new models are necessary, sometimes only valid for very special cases, sometimes explaining a broad range of phenomena at least qualitatively.
To start with an intuitive model, it can be assumed that uncompensated interface spins of the AFM (i.e., the AFM spins whose summation vectors are not zero) couple to the FM. While free uncompensated AFM spins increase the coercivity of the system, pinned uncompensated AFM spins results in an induced unidirectional anisotropy, i.e., the exchange bias [16]. In such models, the exchange bias field can vanish due to roughness which effectively compensates the AFM spins, or it can be overestimated by some orders of magnitude [17].
Néel published a model based on collinear AFM and bulk FM magnetization with uniaxial anisotropy and an uncompensated AFM interface. He found that domains can be created in the equilibrium state which could explain several effects connected with the exchange bias, but on the other hand, the model could not be applied to thin film systems since a bulk FM had to be assumed [18].
Next, the random field model of Malozemoff was published, based on a compensated spin structure and a rough interface, as depicted in Figure 1 [19]. Opposite to the simplest models, however, Malozemoff now allowed domain walls perpendicular to the interface to be formed. This means that in addition to the interface energy, the domain wall energy has to be taken into account [20][21][22]. In other words: while the interface energy is reduced by forming domains with small net spins corresponding to the favored interface coupling, the domain wall energy is increased by forming domains, so that the final domain formation in the energetically favored state depends on the superposition of these two contributions. The formed domains are frozen at low temperatures, thus supporting an exchange bias. Depending on the surface roughness, sensible values of the exchange bias can be reached within this model.
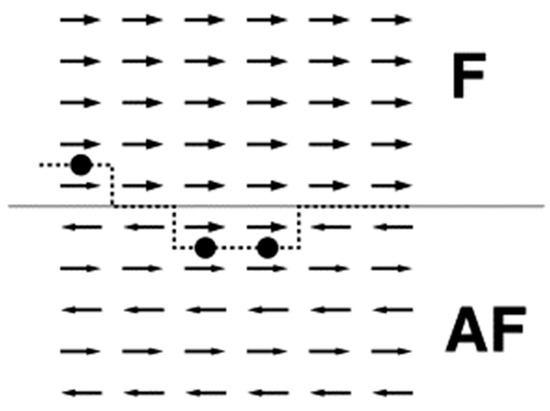
Figure 1. Ferromagnet (F)/antiferromagnet (AF) thin film system with antiferromagnetically coupled interface. The roughness (dashed line) results in frustrated interactions. Reprinted with permission from [19], Copyright 2001 Elsevier.
Mauri’s model included also non-collinear orientations of FM and AFM spins (Figure 2) [23]. By this assumption, domains parallel to the interface were enabled. Interestingly, the exchange bias field calculated within this model was the same as in the historical model of Meiklejohn and Bean who used single-domain AFM and FM with a possible in-plane angle between them and calculated the equilibrium by setting the torque on ferromagnetic and antiferromagnetic moments as zero [24].
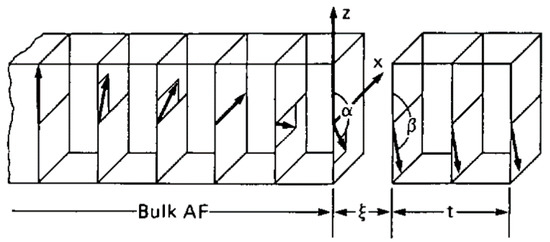
Figure 2. Magnetic model of a bulk antiferromagnet (AFM) (only one sublattice’s spins are shown) in contact with a FM thin film. Here, the uniaxial AFM anisotropy is oriented along the positive z-direction, while the external magnetic field is oriented along the negative z-direction. Reprinted with permission from [23], Copyright 2001 AIP Publishing.
Schulthess and Butler used a three-dimensional Heisenberg-type model with single-crystalline FM and AFM, connected at an even interface with antiferromagnetic coupling. Interestingly, the equilibrium solutions of the Landau–Lifshitz–Gilbert equation revealed states with the ferromagnetic spins being oriented perpendicular to the easy axis of the AFM. If the AFM spins are allowed to show a slight canting, a new uniaxial anisotropy consequently occurred in the ferromagnet. This aforementioned 90° coupling, however, can only explain the increased coercive fields, but not the exchange bias [25][26]. Defects located at the perfectly flat surface, on the other hand, can indeed result in an exchange bias, with approximately realistic values for a spin surplus in the order of magnitude of 1%, as it was also experimentally found [27][28]. The model of Schulthess and Butler thus shows the importance of interface defects, but cannot derive them theoretically.
For a polycrystalline AFM and a single-crystal FM, Stiles and McMichael modeled the exchange bias in a Heisenberg model, partly including the 90° coupling. Depending on the interface coupling strength, they found results similar to Mauri, for the case without 90° coupling, and a strong dependence on the 90° coupling strength, if this is taken into account [29].
While the aforementioned single-crystal and polycrystalline AFMs had only interface defects, the domain state model is based on introducing defects also in the AFM volume [30][31][32][33]. Such an AFM with defects is also called “diluted antiferromagnet” (Figure 3) [34]. Thus, adequate Monte Carlo simulations were performed based on a Heisenberg model, assuming long-range order based on a uniaxial in-plane anisotropy in the FM. The dilution of the upper layer of the AFM could be fixed to investigate the influence of a varying bulk dilution combined with a constant interface roughness. Simulations were performed along a direction slightly different from the easy axis of the ferromagnet.
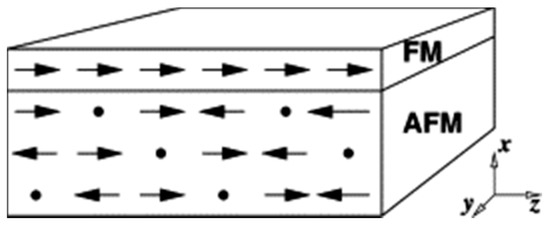
Figure 3. Exchange bias model used in the domain state model, consisting of one ferromagnetic and three diluted antiferromagnetic layers. Reprinted with permission from [34], Copyright 2001 Elsevier.
These simulations showed indeed hysteresis loops which were shifted horizontally and vertically (Figure 4), the latter due to the significant vertical shift of the AFM interface layer (Figure 4b). Interestingly, the latter occurred even during zero-field cooling, i.e., cooling without an external magnetic field. The volume magnetization of the AFM, however, showed this vertical shift only after field cooling [35].
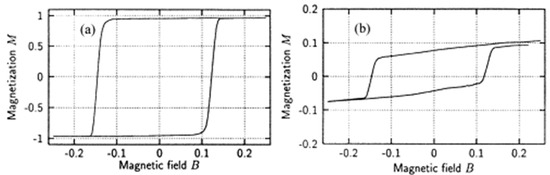
Figure 4. Hysteresis loops of (a) the ferromagnet and (b) the interface layer of the AFM. Reprinted with permission from [34], Copyright 2001 Elsevier.
The authors concluded that the frozen interlayer magnetization of the AFM worked like an additional effective magnetic field on the system, causing the exchange bias effect. The exchange bias was calculated to be proportional to the irreversible domain state magnetization, which corresponds to the vertical shift of the hysteresis loop of the interface layer. The hysteretic behavior of the AFM interface layer and volume was interpreted as the AFM spins switching together with the FM, in this way increasing the coercive fields, while the residual (not switching) part of the AFM interface spins is responsible for the exchange bias.
Another interesting point visible in Figure 4b is that the AFM interface layer hysteresis is not closed, suggesting a reduction of the magnetization during a hysteresis loop, which can explain the aforementioned training effect.
It should be mentioned that, opposite to the model of Malozemoff, applying defects only in the interface layer results in the domain state model in vanishing domains in the AFM [30][31][32][33][34][35].
Another model was suggested by Kiwi et al. who used an AFM with large anisotropy which aimed at simulating Fe/FeF2 and Fe/MnF2, especially the compensated (110) interface [36][37][38]. The large anisotropy in the AFM results in much smaller domain wall widths in the AFM than in the FM [39][40], which on the other hand led to perpendicular FM and AFM spins near the interface and “frozen” spin canting in the AFM interface layer, combined with an incomplete domain wall in the ferromagnet. In this way, they found exchange bias values similar to experimental ones, including even positive exchange bias [38][39][40].
After the few years around 2000 when several exchange bias models based on different assumptions were suggested, there are still many new models being presented, often taking into account special systems or effects and often based on Monte Carlo or micromagnetic simulations.
Radu et al. extended the model by Meiklejohn and Bean by a spin disorder at the interface to model polycrystalline Ir17Mn83/Co70Fe30 thin film systems [41]. They managed not only simulating the measured longitudinal and transverse hysteresis loops, including sharp transitions of the magnetization reversal processes near the easy axis, but also found some, at first glance, unexpected deviations of the experimental and the simulated EB from the usually assume sinus-like dependence on the angular sample orientation.
Investigating Mn52Pd48/Fe bilayers with soft-x-ray magnetic circular dichroism and magnetic reflectivity, Brück et al. found that the Mn atoms neighboring Fe atoms coupled antiferromagnetically to them so strongly that they completely followed the Fe hysteresis loops, so that these Mn atoms could be regarded as an extension layer of the ferromagnet. The next Mn layer, however, exhibited also pinned Mn spins, ferromagnetically coupling to Fe, i.e., aligned antiferromagnetically to the rotating Mn spins [16].
Harres and Geshev published a model for polycrystalline FM/AFM systems. They suggested that for a large enough exchange coupling at the interface, the influence of the AFM results in small domains forming in the FM, while interface grains can be rotatable or fixed. Their model could simulate the non-zero hard axis coercive field (easy and hard axes describe energetically favorable and not favorable orientations of the magnetization), experimentally found in a Co/IrMn film, which was not possible with a model based on a constant rotatable anisotropy, but with the rotatable anisotropy varying along the hysteresis loop, as assumed here [42].
Saha and Victora also investigated polycrystalline biaxial and uniaxial exchange bias systems, based on a micromagnetic simulation in which the ferromagnetic interface grains were coupled to neighboring AFM grains. Using NiFe/NiMn data, reasonable values for coercivity and exchange bias were reached. Interestingly, the crystallographic symmetry of the AFM was found to be correlated with the shape of the system’s hysteresis loop, i.e., showing asymmetric magnetization reversal for biaxial and symmetric hysteresis loops for uniaxial AFM anisotropy, as well as with the training effect [43].
Another grain-level model was developed by Choo et al. [44]. They simulated a soft magnetic ferromagnet coupled to a hard magnetic antiferromagnet, in which the ferromagnet consisted of strongly exchange-coupled grains in a micromagnetic simulation. As the AFM was assumed to have isolated grains of high anisotropy, its magnetic state was assumed to be dominated by thermally activated processes which were modeled by a kinetic Monte Carlo approach. Their model predicted a peak in the coercivity near the blocking temperature due to instability of the AFM layer, connected with a uniaxial contribution to the interlayer exchange energy superposing the unidirectional exchange bias contribution [44]. Such peaks of the coercive field near the blocking temperature are well known from Co/CoO(110) and other systems.
O’Grady et al. also investigated polycrystalline thin films [45]. Summarizing their theoretical work, they found that the EB in such samples is correlated with the thermally stable part of the AFM, as well as with grain size distribution and film thickness. The single AFM grains were found to be independent and to reverse magnetization similarly to the Stoner–Wohlfarth mechanism in ferromagnets. On the other hand, interfacial effects independent from the order in the bulk regions of AFM layer were found. These interface spins showed a tendency to clustering, with these clusters behaving similarly to the aforementioned spin glass states and showing sophisticated interactions with AFM and FM layers [45].
Mangin et al. investigated the ferrimagnetic/ferrimagnetic bilayer system Gd40Fe60/Tb12Fe88 experimentally and by a quantitative model [46], based on unidimensional micromagnetic models for hard/soft magnetic bilayers [47][48]. Under the assumption that the room temperature magnetization configuration inside the TbFe layer is frozen during field cooling, they performed micromagnetic simulations which could well simulate the experimental values of the coercive fields, exchange bias fields and even the vertical loop shift [46]. As they underlined, these experimental results were similar to those found in the more often investigated systems Fe/FeF2 and Fe/FeMn2. It should be mentioned that in their model, there was also the possibility of the formation of a domain wall parallel to the interface, as already discussed in other models [23][46][49].
Morales et al. modeled FM/AFM bilayers with very thin FM layers and used a spring-like domain structure parallel to the interface to quantitatively simulate the deviation from the inverse proportionality of the EB with the thickness of the ferromagnetic layer [50].
Dimitriadis et al. investigated the exchange bias in core–shell nanoparticles of different shapes by an atomistic model, applying a Heisenberg model with uniaxial anisotropy [51]. Depending on the shape and dimension of the nanoparticles, they found negative exchange bias values especially for spherical particles, which were explained by the highly uncompensated interface of such spherical nanoparticles, while a cubical particle showed lower exchange bias due to its mostly compensated interfaces [51].
Using a Monte Carlo simulation, Iglesias et al. also modeled core–shell nanoparticles [52]. They found several qualitative agreements with typical experimental findings, e.g., they also modeled, besides the temperature-dependent horizontal shift of the hysteresis loop and broadening of the coercive field, asymmetric hysteresis loops due to different reversal mechanisms in both loop branches and a vertical shift of the loops due to the same reason. In addition, they found a correlation between the net magnetization of the interfacial shell spins and the exchange bias field [52].
Most recently, simulations showed a correlation of the exchange bias with the Dzyaloshinskii–Moriya interaction, e.g., in MnN(bulk)/Fe systems [53], or a coexistence of exchange bias and Dzyaloshinskii–Moriya interaction, like in Pt/Co/IrMn or Pt/Co/FeMn thin films [54] or Pt/Co/NixOy (Figure 5) [55]. Besides, diverse other simulations of new effects and special systems can be found in the literature; dealing, e.g., with the sign reversal of the EB in LuFe0.5Cr0.5O3 ferrite-chromite due to the competition of various Dzyaloshinskii–Moriya interactions [56], voltage-controlled exchange bias [57], or arbitrarily shaped magnonic nano-waveguides with engineered spin-texture in an exchange-biased bilayer [58].
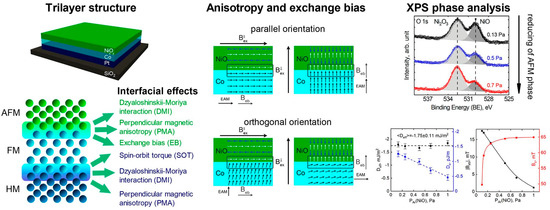
Figure 5. Effects possibly occurring in a trilayer structure of AFM, FM and heavy metal (HM): Dzyaloshinskii–Moriya interaction, exchange bias, spin-orbit torque in the FM and perpendicular magnetic anisotropies in the system NixOy/Co/Pt. Reprinted with permission from [54], Copyright 2021 Elsevier.