1. Extending the Characteristic Polynomial

The characteristic polynomial was firstly encountered (at that time so called 'secular equation') in conjunction with the movement of the planets by famous mathematicians: Euler (1743)^[1], D’Alembert (1750)^[2], Lagrange (1773)^[3], Laplace (1775)^[4], its theory and use was gradually refined by others: Fourier (1822)^[5], Cauchy (1829)^[6], Sylvester (1852)^[7], Hermite (1857)^[8], Weierstrass (1867)^[9], Jordan (1872)^[10], and Kronecker (Kronecker, 1890)^[11].

Once the more general problem were identified as standing for any Hessian matrix by Sylvester (1880)^[12] the characteristic polynomial found its use in the approximate treatment of the Schrödinger's equation (1926)^[13] for the wavefunction (Hartree, 1928)^[14], [15] and Fock (Fock, 1930)^[16], [17] finding the same eigenvector-eigenvalue problem as in the Slater's treatment (1929)^[18], revised later by Hartree & Hartree (1935)^[19].

While the first reports relating to the use of the characteristic polynomial in relation with the chemical structure appears shortly after the discovery of wave-based treatment of microscopic level from Hückel (1931)^[20], the roots of this extended version of the characteristic polynomial can be attributed to the assignment of the individual electronic energies (ε_i), as accounted for the first time by Coulson in 1937^[21], 1940^[22], and 1950^[23].

The characteristic polynomial (ChP) is the natural construction of a polynomial in which the eigenvalues of the [Ad] are the roots of the ChP as it follows:

λ is an eigenvalue of [Ad] ↔ it exists [v] ≠ 0 eigenvector such that λ·[v] = [Ad]·[v] →

(λ·[Id]-[Ad])·[v] = 0; since v ≠ 0 → [λ·Id - Ad] is singular → det([λ·Id - Ad]) = 0

The characteristic polynomial ChP is a polynomial in λ of degree the number of atoms, ChP(λ) = det([λ·Id - Ad]).

As introduced in (Joița & Jäntschi, 2017)^[24], the Extended Characteristic Polynomial (EChP) of a chemical structure is defined similarly (see Table 1) with the Characteristic Polynomial (ChP) of its associated topology (T).

Table 1. Topology, Chemistry and Geometry for Ethanimine (HN=CH-CH₃)

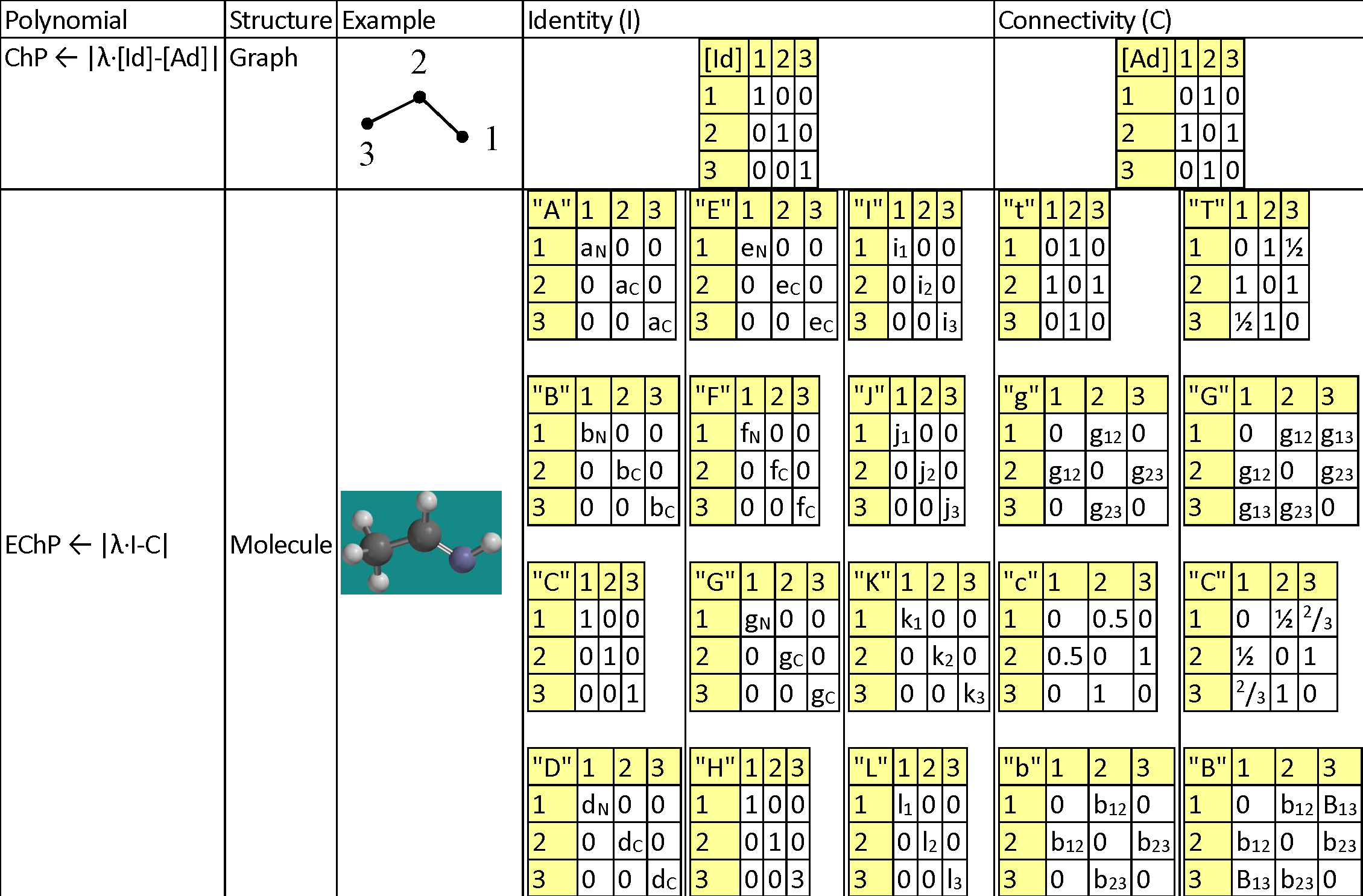Legend for replacement values: aC = 12/294; aN = 14/294; bC = 3915/3915; bN = 77.355/3915; dC = 2267/30000; dN = 1495/30000; eC = 2.55/4.00; eN = 3.04/4.00; fC = 1086.2/1312.0; fN = 1402/1312; gC = 3915/3915; gN = 63.15/3915; i1 = -0.738; i2 = 0.497; i3 = -0.756; j1 = -0.593; j2 = 0.090; j3 = -0.653; k1 = -0.628; k2 = 0.097; k3 = -0.734; l1 = 0.0; l2 = 0.0; l3 = 0.0; g12 = 1/1.290; g13 = 1/2.451; g23 = 1/1.496; b12 = 1/1.869; b23 = 1/0.905; B13 = 1/(1/1.869+1/0.905).

2. Extended Characteristic Polynomial

A natural extension of ChP is to store in the identity matrix (instead of unity) non-unity values accounting for different atoms (and then the [Id] matrix is replaced by a generic matrix, [I_p], having more than one alternative to be filled with values), as well as to store in the adjacency matrix (instead of unity) non-unity values accounting for different bonds (and then the [Ad] matrix is replaced by a generic matrix, [C_q], having more than one alternative to be filled with values). Then the extended characteristic polynomial is defined by EChP(λ; p, q) = det([λ·I_p - C_q]).

The proposed alternatives for identifying the atoms are p ∈ {"A", "B", "C", "D", "E", "F", "G", "H" "I", "J", "K", "L"}, being exemplified in Table 1 and having the following meanings: Atomic mass ("A"), Boiling point ("B"), Count ("C"), Density ("D"), Electronegativity ("E"), First ionization potential ("F"), Melting point ("G"), Hydrogen connections ("H"), Electrostatic charge ("I"), Mulliken charge ("J"), Natural charge ("K"), and Spin ("L").

The proposed alternatives for identifying the bonds are q ∈ {"t", "g", "c", "b", "T", "G", "C", "B"}, being exemplified in Table 1 and having the following meanings: being derived of adjacencies ({"t", "g", "c", "b"}) and on distances {"T", "G", "C", "B"}, as classical topological measures ("t" and "T"), inverses of geometrical distances ("g" and "G"), inverses of conventional bond orders ("c" and "C"), and inverses of Mulliken bond orders ("b" and "B").

It should be noted that all proposed alternatives keep the symmetry alive in both identity (I_p) and connectivity (C_q) replacements of identity matrix ([Id]) and adjacency matrix ([Ad]), keeping thus the Hessian property of their linear combination.

Also it should be noted that any value greater than 1 as entry in any of identity (I_p) and connectivity (C_q) matrices is dangerous to the computations of the associated characteristic polynomial (any number greater than 1 easily diverges producing huge numbers when is risen at a natural power), and as such, proportion (from 0 to 1, or from -1 to 1) scales must be used whenever is possible to keep at reasonably low level the evaluations for the extended version of the characteristic polynomial.

A series of constant values has been used for a group of atomic properties ({"A", "B", "D", "E", "F", "G", "H"}) by keeping the track between chemical elements through their atomic number (Z) as listed in Table 2.

Table 2. List of the atomic numbers associating atomic properties with chemical elements

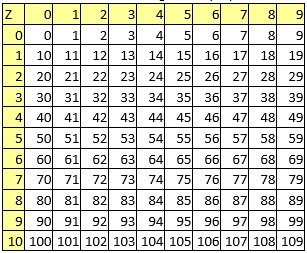
In the first element of the list (line 0 column 0 in Table 2) it has been kept the scale of the atomic property - the value to be used to divide all other values when are to be used as atomic property descriptors.

Following tables (from Table 3 to Table 9) lists the constants used for each chemical element.

Table 3. Atomic masses

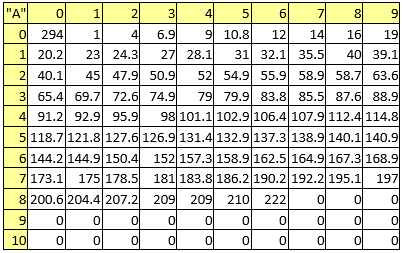
Table 4. Boiling points

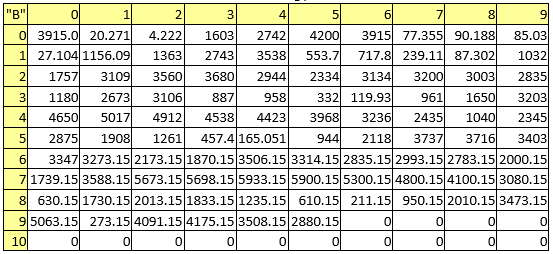
Table 5. Densities

Table 6. Electronegativities

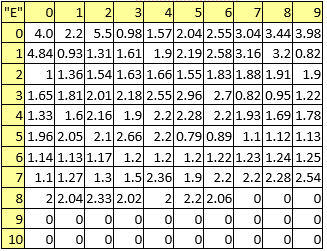
Table 7. First ionization potentials

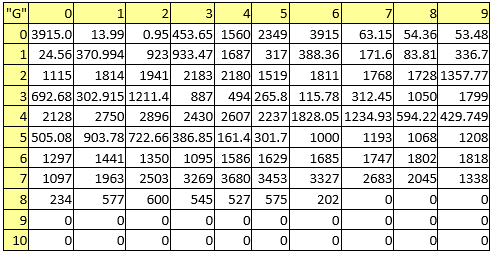
Table 8. Melting points

Table 9. Valences (to be used for Hydrogen connections)

The valences (Table 9) are to be used to calculate the number of attached Hydrogen atoms based on the bonds and their orders (by subtracting the sum of the bond orders form the valence), while the counts ("C" property) is trivial - always 1. For the remaining atomic properties ({"I", "J", "K", "L"}), those are molecule-dependent and are expected to be provided from energy calculations on the molecule. As can be observed excepting Hydrogen connections ("H", valences listed in Table 9) the rest of the atomic properties ({"A", "B", "C", "D", "E", "F", "G"}) are molecule-independent.

As exemplified also in Table 1, the connectivities are to be calculated as follows:

• "t" as adjacency matrix ([Ad]) provides;
• "T" as topological distance matrix ([Di]) provides, inversed ([C_T]_i,j = 1/[Di]_i,j for i ≠ j, 0 otherwise);
• "G" as geometrical distance matrix ([Dxyz]) provides, inversed ([C_G]_i,j = 1/[Dxyz]_i,j for i ≠ j, 0 otherwise);
• "g" as dot product of geometrical distances ([Dxyz]) and adjacency ([Ad]) matrices ([C_g]_i,j = [Dxyz]_i,j[Ad]_i,j);
• "C" and "B" construct first an replacement for adjacency matrix by replacing the values of 1 with the inverse of the bond order ("C" as classical bond orders and "B" as Mulliken bond orders) and calculate a distance matrix ([DC], [DB]) by using this new adjacency matrix, finally inversing those values ([C_C]_i,j = 1/[DC]_i,j for i ≠ j, 0 otherwise; [C_B]_i,j = 1/[DB]_i,j for i ≠ j, 0 otherwise);
• "c" and "b" as dot products of previously calculated [DC] and [DB] matrices with adjacency ([C_c]_i,j = [C_C]_i,j[Ad]_i,j; [C_b]_i,j = [C_B]_i,j·[Ad]_i,j).

Parameterized by the atomic property (p ∈ {"A", "B", "C", "D", "E", "F", "G", "H" "I", "J", "K", "L"}) and by the connectivity (q ∈ {"t", "g", "c", "b", "T", "G", "C", "B"}) the extended characteristic polynomial become a family of polynomial functions (EChP(λ; p,q)).

3. Practical use of the Characteristic Polynomial extension

It has previously shown in (Bolboacă & Jäntschi)^[25] how the classical characteristic polynomial can be used to link the chemical structure with measured properties and activities of the molecules build up from hydrocarbons.

In the same manner the EChP(λ; p, q) may serve to link the chemical structure with measured properties and activities of the molecules build up from any chemical elements.

One strategy is to evaluate the EChP(λ; p, q) polynomial in a series of evenly spaced points from -1 to 1. For three digits rational arguments (λ = -1.000, -0.999, …, -0.001, 0.000, 0.001, …, 0.999, 1.000) are 2001 evaluation points.

By multiplying with the number of alternatives from identity (I_p) and connectivity (C_q) choices (p and q), the number of individuals in the EChP family is 2001·12·8 = 192096. Three linearization operations can be applied ("I", "R", "L") through the functions f_I(x) = x, f_R(x) = 1/x and f_L(x) = ln(x) increasing the number of individuals in the EChP family to 576288. To keep the track of each individual, the naming convention is: L₁L₂L₃C₀D₁D₂D₃ where L₁ ∈ {"I", "R", "L"} for linearization, L₂ ∈ {"A", "B", "C", "D", "E", "F", "G", "H" "I", "J", "K", "L"} for identity, and L₃ ∈ {"t", "g", "c", "b", "T", "G", "C", "B"} for connectivity with the correspondences above given, while C is "N" for λ < 0, "0" for λ = 0, and "P" for λ > 0, and D₁D₂D₃ is the group of (3) digits from the evaluating value of λ (varying from "000" to "999").

In (Joița & Jäntschi, 2017)^[24] paper is given an application of the use of EChP for a series of C₂₀ fullerene congeners obtained by replacing in a patterned manner carbon atoms with nitrogen and boron. The obtained results revealed good EChP explanatory capabilities of the structure-property relationship for the area (r²_adj = 0.994) and for the volume (r²_adj = 0.946) of the series of 46 C₂₀ fullerene congeners.

It should be noted that the constants give in Tables 3 to 9 to be used as scaling factors for the atomic properties (as opposite to the atomic properties itself, which were taken from measured or published data) are more or less arbitrary and can be subject to debate, but the principle of constructing EChP is sound. Further studies are necessary to construct a best fit for the scaling factors (eventually made by parameterizing them).