1000/1000
Hot
Most Recent
This video is adapted from 10.3390/e20080593
The refinement axiom for entropy has been provocative in providing foundations of information theory, recognised as thoughtworthy in the writings of both Shannon and Jaynes. A resolution to their concerns has been provided recently by the discovery that the entropy measure of a probability distribution has a dual measure, a complementary companion designated as “extropy”. Researchers report here the main results that identify this fact, specifying the dual equations and exhibiting some of their structure. The duality extends beyond a simple assessment of entropy, to the formulation of relative entropy and the Kullback symmetric distance between two forecasting distributions. This is defined by the sum of a pair of directed divergences. Examining the defining equation, researchers notice that this symmetric measure can be generated by two other explicable pairs of functions as well, neither of which is a Bregman divergence. The Kullback information complex is constituted by the symmetric measure of entropy/extropy along with one of each of these three function pairs. It is intimately related to the total logarithmic score of two distinct forecasting distributions for a quantity under consideration, this being a complete proper score. The information complex is isomorphic to the expectations that the two forecasting distributions assess for their achieved scores, each for its own score and for the score achieved by the other. Analysis of the scoring problem exposes a Pareto optimal exchange of the forecasters’ scores that both are willing to engage. Both would support its evaluation for assessing the relative quality of the information they provide regarding the observation of an unknown quantity of interest. Researchers present our results without proofs, as these appear in source articles that are referenced. The focus here is on their content, unhindered. The mathematical syntax of probability they employ relies upon the operational subjective constructions of Bruno de Finetti.
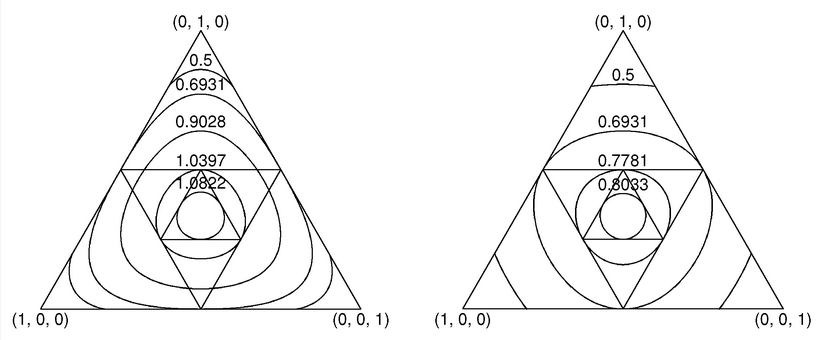
Figure 1. On the left are equal-entropy contours of distributions within the 2D unit-simplex, S2. On the right are equal-extropy contours of distributions. The inscribed equilateral triangles exhibit sequential contractions of the range of the complementary transformation from P3 vectors to their complements q3, and then in turn from these q3 vectors to their complements, and so on. The fixed point of all contraction mappings is the uniform distribution (pmv).
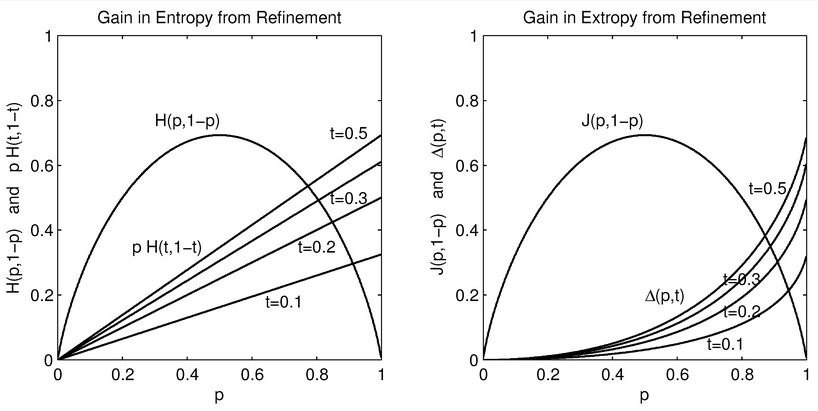
Figure 2. The entropies (at left) and extropies (at right) for refined distributions equal the entropy/extropy for the base probabilities, , plus an additional component. This component is linear in p at the constant rate for entropy, and non-linear in p for extropy at a rate that increases with the size of p.
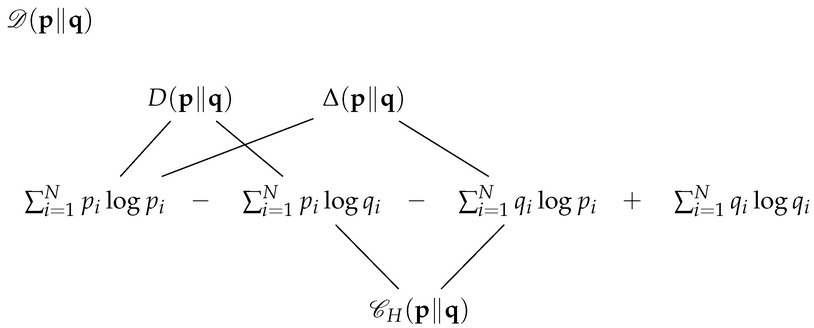
Figure 3. Schematic display of the symmetric Kullback divergence , which shows that it can be generated equivalently by three distinct pairs of summands. These are specified by the directed divergence , by an alternative difference , and by the cross-entropy sum .
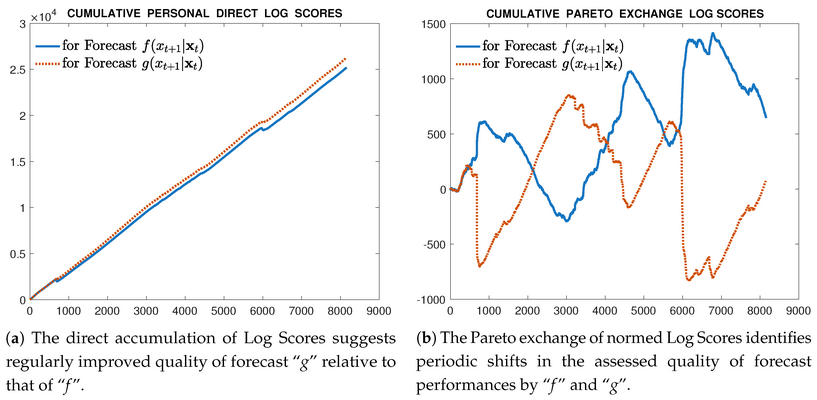
Figure 4. Comparative results of accumulating Direct Scores and Pareto exchanged Scores for the same two forecasting distributions and data sequence.