1000/1000
Hot
Most Recent

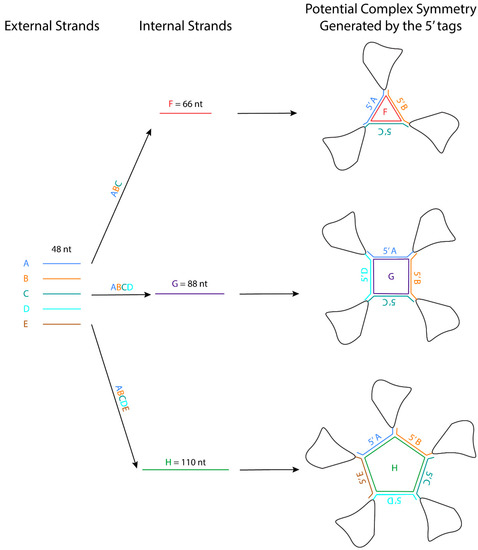
The crystal packing strategies described in this entry can reduce the flexibility of the interacting regions. Some of these crystal packing modules generate symmetry, which should promote crystallization because proteins with molecular symmetry are known to crystallize more readily than those without molecular symmetry. For example, the kissing loop complex generates two-fold symmetry, the G-quadruplex generates a four-fold symmetry, and the 3WJ junction has been further engineered to form a stable planar triangle, square, and pentagon using oligonucleotides.
Structural biology of RNA molecules began in the 1960s with the stepwise resolution improvement of the yeast tRNA Phe crystal structures [1][2][3]. The cloverleaf structure of the tRNA is likely the first introduction to the RNA structure encountered by many science students. The tRNA crystal structures unveiled how specific tertiary interactions maintain the three-dimensional fold of the RNA molecule, and how the three-dimensional architecture enables its role in protein translation. The next breakthrough came in the crystal structures of the ribozymes [4][5][6] and self-splicing introns [7], which demonstrated how RNA can fold into an architecture capable of carrying out enzymatic catalysis. These early RNA crystal structures set the stage for the structural investigation of large RNA-containing macromolecular complexes such as the ribosome and the spliceosome that are key players in the central dogma of molecular biology [8][9][10]. The millennium began with the discovery of many more types of non-coding RNAs (e.g., microRNAs, riboswitches, lncRNAs; see [11] for a comprehensive review). X-ray crystallography has remained a critical experimental approach to understanding the molecular mechanisms enabling these non-coding RNAs to perform extraordinarily diverse biological functions.
Crystallization of RNA molecules for structural determination and molecular interaction elucidation is often more challenging than the crystallization of soluble proteins [12][13]. This in part explains why RNA-only structures account for less than 0.7% of the biomolecular crystal structures deposited in the Protein Data Bank (PDB). As an equilibrium process, crystallization is governed by both the properties of the soluble molecule and the nature of its crystalline state. Although RNA duplexes are highly stable thermodynamically, the higher-order folding landscape of RNA is often complex, with multiple competing minima, as well as kinetic traps [14][15][16][17]. This results in conformational heterogeneity in the solution [18]. The molecular surface of folded RNAs is dominated by a regular array of negatively charged phosphates that can lead to packing (through counterions) into crystals that are disordered at the atomic level [19][20][21]. Strategies for improving conformational homogeneity of folded RNAs are generally useful for any biophysical or structural study of this biomolecule, while techniques for enhancing the formation of improved crystal contacts are often necessary for the successful application of X-ray, neutron, or electron crystallography [12][22][23][24][25][26].
The idea of engineering nucleic acid sequence to promote crystal contacts originated in the work of Schultz et al., where they successfully crystallized the E. coli catabolite gene activator protein complexed with its DNA-binding site after scanning through 26 different DNA sequences [27]. Over the years, several molecular engineering techniques have been developed to favor ordered crystal packing of RNAs (e.g., [28][29][30]). Furthermore, optimized crystallization conditions and sometimes post-crystallization treatments have also been crucial for success in RNA crystallography [31][32]. In this review, we highlight new engineering strategies for RNA crystallization, as well as techniques that have proved successful in aiding the growth of diffraction quality crystals in the past [33]. In addition, we emphasize considerations that may affect their adoption and use in different RNA contexts beyond where they were initially developed [34]. This review may be of interest to nucleic acid crystallographers who seek to expand their repertoire of engineering tools to tackle the crystallization of challenging RNA targets.
When adjacent complementary sequences hybridize to form an RNA duplex, a hairpin or stem loop structure is formed. Proteins can bind some loops (e.g., spliceosomal proteins U1A [35], U2A’/B” [36], the pseudouridine synthase TruB [37]). Other loops can serve as folding nucleation sites, confer stability, and participate in tertiary RNA interactions (e.g., the UUCG tetraloop [38]). Tetraloops and kissing loops are the most common hairpin loops that engage in tertiary RNA interactions. Replacing flexible structures between complementary sequences by tetraloops or kissing loops is a common strategy to promote the formation of well-packed crystals by removing undesirable elements that hinder crystallization and generating potential interfaces for crystal packing. We review several specific examples below to illustrate these principles in action.
A tetraloop is a 4-nt loop that caps a stem. The GNRA and the UNCG (N = any nucleotides, R = either purine) families are the most common types found in natural RNAs. The GNRA tetraloop typically adopts a U-turn conformation, characterized by the first nucleobase forming a hydrogen bond with the backbone of the fourth nucleotide. This base to backbone interaction positions the first nucleobase to form a stacking (π-OP) interaction with the oxygen of the phosphate backbone of the third nucleotide. The UNCG tetraloop typically adopts a Z-turn conformation, characterized by the first and fourth nucleotides forming a trans Sugar/WC interaction and an unusual ribose backbone conformation that allows the formation of a stacking (π-O4′) interaction between the fourth nucleobase and the ribose oxygen of the third nucleotide [39]. The GNRA tetraloops are more commonly found to engage in tertiary interactions. In contrast, the UNCG tetraloop has exceptional thermostability, and it is typically used to replace flexible regions undesirable for crystal packing. The thermal stability of the UNCG tetraloop is mainly contributed by hydrogen bonds between the 2′-hydroxyl groups of the first and second sugar moiety with the Hoogsteen edge of the base of the fourth nucleotide [40][41]. Interestingly, the core of the four-way junction is recently identified as a receptor for a UNCG tetraloop [42]. However, a four-way junction is not easy to implement in other structural contexts. We will consider tetraloops with their cognate receptors that are convenient to incorporate in different RNA structures to promote loop to stem contacts.
The GAAC is a non-GNRA tetraloop found in group II introns and has a folding geometry distinct from the GNRA fold [43][44]. Instead of a trans Sugar/Hoogsteen base pair between the first and fourth nucleotide, a trans Sugar/WC base pair was observed. As a result, the first base of the loop no longer stacks with the 5′ WC base pair of the stem. A modular 20-nt receptor was identified by in vitro selection with a binding affinity (kD ~ 2.4 nM) comparable to that of the GAAA/GAAA-R interaction [45] ( Figure 1 C-ii). The GAAC/GAAC-R loop to stem interaction may have a different orientation compared to that formed by GAAA/GAAA-R. This is based on the relative catalytic efficiency observed in the in vitro selection system. The tetraloop and its receptor are engineered in a ribozyme structural fold, and the ribozyme catalysis depends on their interaction. Although the GAAC/GAAC-R motif resulted in catalysis, the efficiency was ~30% less than that observed for the GAAA/GAAA-R motif [46]. The authors attributed the catalytic difference to a variation in the orientation of the interaction motif. Thus, the GAAC/GAAC-R motif could create alternative packing geometry compared to the GAAA/GAAA-R motif. Unfortunately, no structural confirmation of the interaction is available to date. Nonetheless, a chemical probing experiment suggests that the WC edges of the middle two As interact with the receptor [45].
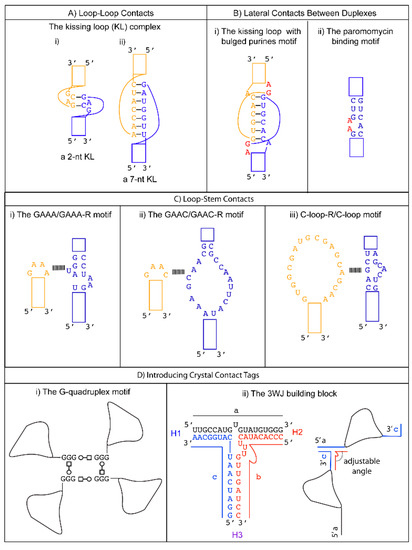
The C-loop is a recurrent motif characterized by an asymmetric internal loop. As observed in ribosome structures, the main structural function of the C-loop is to increase the helical twist of the stem loop where it is embedded so that the hairpin loop can engage in optimal tertiary interaction [46]. Although it does not naturally participate in tertiary interaction, a 20-nts loop receptor (C-loop-R) in the form of a loop was identified by in vitro selection [54] ( Figure 1 C-iii). Therefore, a possible crystal packing design incorporates a C-loop motif into a stem, and the C-loop-R could be inserted as a stem loop. Unfortunately, no structural information of the interaction is available. However, chemical probing experiments suggest that the C-loop motif binds C-loop-R via non-WC interactions [54].
When prior knowledge crystallization modules and rationale design approaches fail, a stochastic process might succeed. One example is the exciting “in crystallo” selection in which error-prone PCR generates a pool of 10 million mutant DNA templates (each DNA containing 0–2 mutants). Next, the templates are transcribed with Phage T7 RNA polymerase, gel purified, and then used in crystallization experiments using conditions known to give crystals of the wild-type RNA [13]. The largest crystals are isolated, dissolved, reverse transcribed, and sequenced. In principle, the selection process is repeated for several cycles to obtain better crystals. When the second round of selection was applied to the P4-P6 domain of Tetrahymena, smaller crystals were obtained, so the selection process was abandoned. The P4-P6 domain crystallizes with two molecules in the asymmetric unit. In the first cycle, wild-type molecules were present; they may have acted as crystallization chaperones for the mutant molecules because a wild-type molecule paired with a mutant molecule in the asymmetric unit. The mutant RNAs were made and crystallized individually, and structures were determined from four of the mutants. Some of the mutant RNAs gave inferior diffraction in the absence of the wild-type RNA. The authors suggest that the selection process may be more stringent in selecting mutants that give crystals when only one RNA molecule can occupy the asymmetric unit. The authors did not explore the combination of two or more mutations to determine if the multi-mutant RNA could give crystals that diffract to a higher resolution than the wild-type RNA. The authors found improvement in the electron density maps around the mutant sites compared to the wild-type structure by local structural rearrangements in loops and new intermolecular contacts [13]. Their results suggested that bulged residues could be walked along the chain in either direction without disrupting the core structure. They also suggest that “bulge engineering” could be applied to any unpaired surface regions. The “in crystallo” selection experiments lead to the discovery of one potentially universal RNA crystal engineering tactic, and it is reasonable to expect that additional principles will be suggested by the structures of other mutant RNAs from future “in crystallo” selection experiments. While this study failed to improve diffraction quality, it demonstrated that “in crystallo” selection can be applied to RNA, and it opened a new approach to promoting RNA crystallization.
Another under-exploited area is the enhancement of the RNA structure stability by introducing X bonds between halogen atoms in bases and the backbone oxygen atoms. These interactions have been better characterized in DNA [55]. Bromine atoms are routinely introduced in synthetic RNAs to obtain experimental phases for structure determination. The position of the halogenated base within an RNA fragment can shift the equilibrium between duplex formation and hairpin formation, so several constructs may have to be tested [56]. Constructs could be prescreened for their conformation by native gel electrophoresis.
Another rapidly emerging structure determination technique of possible relevance to RNA crystallography is microcrystal electron diffraction (MicroED). These experiments are conducted with a transmission electron microscope in diffraction mode. The advantage of this method is that high-resolution diffraction data can often be obtained from nanocrystals (at least one dimension smaller than 100 nm) that are a billionth of the volume considered suitable for X-ray diffraction studies [57]. The disadvantages are the very limited access to instruments that can rotate the sample during data collection. The early successes with peptides and small proteins suggest that it might work well with smaller RNAs. Further technological advancements may be required for success with crystals of larger RNAs.
With the remarkable advancement in structural prediction algorithms and Cryo-EM, one may ask if there is still relevance in designing crystal contacts for nucleic acid structure determination. While the accuracy of AlphaFold2 is remarkable for predicting protein structures [58][59], it may still take some time for nucleic acids structure prediction due to the sparsity of structures available to train a neural network model for RNA structure prediction. Suppose the deep learning approach eventually succeeds at making accurate predictions of nucleic acid structure. In that case, can the deep learning models be harnessed to assist in engineering crystal contacts? Alternatively, other computational approaches from the protein re-design field, like the dead-end elimination theorem [60], could be used to perform the above-mentioned bulge walking in-silico in the presence of all of the surrounding symmetry mates. Such a computational approach to crystal lattice engineering should now be within reach thanks to the increased computational power available from GPUs. For instance, molecular docking of large libraries of small molecules against ensembles of protein structures is now practical thanks to GPUs. Ultimately, predicted structures will never replace the need for experimentally-determined structures designed with biological functions in mind.
With the recent “resolution revolution” in Cryo-EM, Cryo-EM has yielded several low-resolution structures of single-stranded RNAs as small as 40 kDa, suggesting that Cryo-EM will generally apply to large and medium-sized RNA structures [61][62]. It remains to be shown if such low-resolution structures are accurate enough to inform the design of constructs for crystallization to obtain high-resolution structures. Cryo-EM has great promise in the study of RNAs that have conformational heterogeneity, especially if the alternate conformations can be clustered in a modest number of conformations. With suitable clustering algorithms, most of the conformations of a small ensemble can be characterized from a single sample. Thus, Cryo-EM can give multiple structures from one sample. If the conformational heterogeneity cannot be parsed into distinct clusters, it can be addressed computationally at the expense of reduced resolution of the Cryo-EM map.
The crystal packing strategies described in this review can reduce the flexibility of the interacting regions. Some of these crystal packing modules generate symmetry, which should promote crystallization because proteins with molecular symmetry are known to crystallize more readily than those without molecular symmetry [63]. For example, the kissing loop complex generates two-fold symmetry, the G-quadruplex generates a four-fold symmetry, and the 3WJ junction has been further engineered to form a stable planar triangle, square, and pentagon using oligonucleotides [64]. These polygons are formed using different external 48-nt strands that form the side and one internal strand that base pairs with each external strand like a tape ( Figure 2 ). The affinity of the strands to form the polygon is in the order of ~20 nM, and the formation is highly efficient. An RNA structure can potentially be engineered at the 3′ end of each external strand, allowing the RNA to assemble into a higher-order complex with the polygon in the middle. The addition of these polygons could facilitate Cryo-EM studies by increasing the molecular weight of the RNA and overcoming preferred orientation. If the attached RNAs of interest have consistent orientations with regards to the polygon, they can also provide a rotational symmetry during 3D reconstruction.