2. Analyses and Comparisons between IRI and IRTAM
The results shown in the previous sections are here summarized through the residual deviation ratio
Rcw defined in
Section 4.
Rcw is a statistical parameter that in general is very suitable to assess definitively the performance of one model over another. To this end, the IRI and IRTAM performances are evaluated analyzing the distributions (in a logarithmic scale) of the residuals’ deviation ratio calculated on both the full
foF2 ionosonde/COSMIC dataset (
Figure 1) and the full
hmF2 ionosonde/COSMIC dataset (
Figure 2).
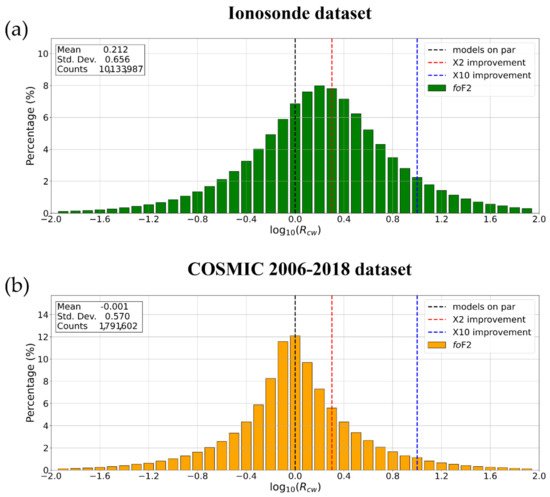
Figure 1. Probability distributions of the residuals’ deviation ratio in a logarithmic scale, log10(Rcw), between IRI and IRTAM models calculated on the (a) entire ionosonde and (b) COSMIC foF2 datasets. The mean, standard deviation, and counts values are reported in the upper left corner of each plot. The dashed vertical lines indicate, respectively, when the models are on par (in black), IRTAM improves IRI by a factor of 2 (in red), and IRTAM improves IRI by a factor of 10 (in blue).
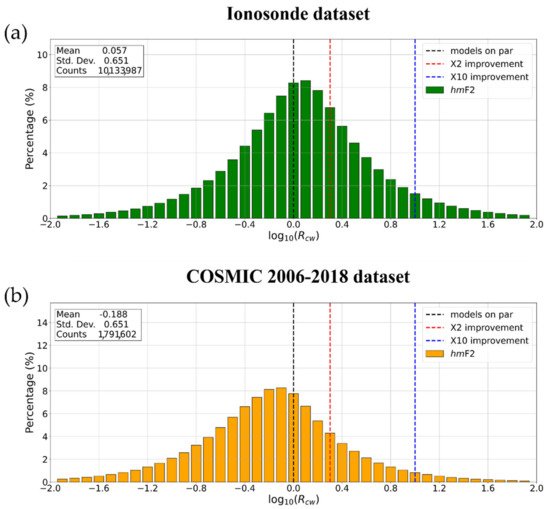
Figure 2. Same as Figure 1 but for hmF2.
The log10(Rcw) distribution shown in Figure 1a is clearly “shifted” towards the positive values. Specifically, the mean value of the distribution equal to +0.212 highlights that overall IRTAM performs better than IRI by a factor of about 1.6 when considering the foF2 ionosonde dataset. Instead, the log10(Rcw) distribution shown in Figure 1b is quite symmetric with respect to the zero value. This fact is strongly supported by the mean value of the distribution, which is equal to −0.001. Therefore, the IRI and IRTAM performances can be considered equivalent when considering the COSMIC foF2 dataset.
The log10(Rcw) distribution shown in Figure 2a is quite symmetric around the zero. Specifically, the mean value of the distribution equal to +0.057 (which corresponds to an improvement factor of about 1.14) highlights that IRTAM and IRI provide quite comparable outputs when considering the hmF2 ionosonde dataset. The log10(Rcw) distribution shown in Figure 46b is clearly “shifted” towards the negative values. Specifically, the mean value of the distribution equal to −0.188 points out that IRI performs better than IRTAM when considering the hmF2 COSMIC dataset by a factor of about 1.5.
The same analysis based on log
10(
Rcw) distribution was applied by Galkin et al.
[18] on a dataset of
foF2 values recorded by 59 ionosondes during May–June 2019. They found results very similar to the ones shown in
Figure 1a, with IRTAM improving IRI by a factor of about two (about 0.3 in the logarithmic scale of
Figure 1). The slight differences are due on the one hand to the fact that to test IRTAM Galkin et al.
[18] used only data from assimilated stations, while in this study we used also non-assimilated stations, and on the other hand to the larger extension of our dataset covering different seasons and solar activity levels. Results similar to those of Galkin et al.
[18] were obtained also by Vesnin
[29] by considering a larger dataset covering one solar cycle, but again using only data from assimilated stations to test the model. Vesnin
[29] investigated the IRTAM performance also for
hmF2 and found that IRTAM improved IRI by a factor of about 1.8. However, in that analysis the oldest Bilitza et al.
[30] hmF2 IRI option was used as comparison. When using the newest Shubin et al.
[31] default IRI
hmF2 option, we find much lower differences between IRTAM and IRI, thus confirming the very important step forward made by IRI about the
hmF2 modeling, as on the other hand recently outlined by different authors
[32][33][34].
Figure 1 and
Figure 2 confirm the general picture outlined by the analyses described in Section 5, Section 6, Section 7 and Section 8, i.e., the comparison with ionosonde data highlights how IRTAM significantly improves the
foF2 prediction made by IRI, while for
hmF2 the performances are quite similar between the two models. Since IRTAM assimilates both
foF2 and
hmF2 from the GIRO network, we would have expected a similar improvement also in the
hmF2 prediction. Besides the obvious differences due to the application of the newest Shubin et al.
[31] IRI
hmF2 default option, two important points need to be highlighted. First, the IRTAM
hmF2 description is based on the mapping procedure introduced by Brunini et al.
[35], which introduces residuals in the range from −10 to 10 km when compared to the original
hmF2 values obtained from the Bilitza et al.
[30] formulation. The second point is inherent to the
hmF2 derivation from ionograms. In fact, while
foF2 is a parameter that is directly obtained from ionograms as the maximum ordinary frequency reflected by the ionosphere,
hmF2 has to be derived trough a mathematical inversion procedure that, starting from critical frequencies measured at different virtual heights, allows obtaining the electron density values at real heights
[36]. This inversion procedure is sensitive to different possible error sources due to the E-valley presence, the interpretation of the F2-layer cusp made by ARTIST, and in general the quality of the ionogram echo traces. All of these matters may represent possible sources of error, that are estimated in the order of 10 km
[37]. From the above considerations, it clearly emerges that to obtain reliable
hmF2 values is more difficult than to get
foF2 ones, even with data assimilation. This is a point that requires further improvements and refining of both the data assimilation procedure and the measurement technique itself.
The comparison with the F2-layer peak characteristics derived from COSMIC RO showed a general worsening of the IRTAM performances in comparison with the IRI ones. Specifically, the comparison with the COSMIC dataset (Figure 20 and Figure 41) highlighted that IRTAM improves the IRI foF2 and hmF2 predictions mainly in regions characterized by a dense ionosonde network. This suggests the extent to which IRTAM is tied to data assimilated by ionosondes and to the corresponding spatial distribution. Since assimilated data are used by IRTAM to update the coefficients of the spherical harmonic analysis underlying the IRI description, we would have expected that the improvements were not restricted to the ionosondes’ locations but would embrace at least the whole latitudinal sector where assimilated ionosondes are located. Moreover, the IRTAM description should fade towards that of the IRI in regions where the effect of the assimilated data can be considered negligible. These two points are very important, impacting on IRTAM global performances, and need to be deeply investigated for future versions of IRTAM. Currently, IRTAM assimilates data from about 60 GIRO Digisondes. With the ever-increasing number of available Digisondes, able to provide real-time data, and as a consequence of their more homogeneous spatial distribution, a continuous improvement of the IRTAM performance is expected. However, even if in the future the availability of ionosonde data should increase for both the time resolution and the spatial coverage, the fact that IRTAM is so tied to the underlying IRI model (i.e., to the URSI formalism) represents a limit for the improvement and development of IRTAM itself. In fact, IRTAM through NECTAR, to minimize at assimilation sites the mismatch between measured and IRI modeled values, calculates the corrections to be added to the URSI coefficients, but the order of the diurnal and spatial harmonics is left unchanged. This means that steep spatial gradients and fast time variations that are below the limits that can be resolved with the current spatial and temporal resolution of the URSI formalism would not be represented by IRTAM, even with an increased availability of assimilated data. Since steep spatial gradients and fast time variations are customary under specific Space Weather conditions, and the aim of data-assimilation methods is the reliable representation of such conditions, this poses serious limitations for the IRTAM model that its developers should bear in mind in the future.
3. Conclusions
In the present paper, we compared the IRI and IRTAM models; the latter, being a real-time version of IRI, is based on the assimilation of ionosonde measurements. In order to assess the performance of the two models, two different datasets have been considered: (1) foF2 and hmF2 from ground-based ionosonde observations; (2) foF2 and hmF2 from space-based COSMIC RO observations. Through different analyses and comparison methodologies, we highlighted the main performances exhibited by both IRI and IRTAM for different locations and under different diurnal, seasonal, solar and magnetic activity conditions.
The main results of the study are:
-
When ionosonde observations are considered for validation, IRTAM improves significantly the IRI foF2 modeling while it slightly improves the IRI hmF2 modeling.
-
When COSMIC observations are considered for validation, IRTAM improves neither the IRI foF2 modeling nor the IRI hmF2 modeling.
These results highlight that IRTAM, in contrast to most of assimilation models, has ample room for improvement. The points that in our opinion deserve specific attention are: the bad performance of IRTAM when modeling foF2 at low latitudes; the global hmF2 modeling made by IRTAM which is often unreliable, especially in areas far away from the assimilating sites, where the representation made by IRTAM is at times really different from that of the IRI background; the fact that IRTAM performances are too dependent on the assimilated ionosondes location.
The improvement in the near real-time specification of the ionospheric F2-layer peak characteristics is becoming more and more important nowadays for telecommunication purposes and for Space Weather applications in general. For example, Hartman et al.
[38] have recently applied IRTAM as the Floating Potential Measurement Unit (FPMU) back-up system that will be used to support the International Space Station (ISS) program. IRTAM
foF2 maps were used by Froń et al.
[39] to provide global maps of the ionospheric equivalent slab thickness (
τ) parameter that are delivered through the GAMBIT Explorer software (http://giro.uml.edu/GAMBIT, accessed on 3 August 2021). An improved real-time specification of
τ on a global basis is very important because this parameter describes the shape of the ionospheric electron density profile; thus, an improved specification of
τ can help empirical models such as IRI in the description of the profile shape, especially the topside part
[40][41][42][43].
Since in the incoming years the applications based on a near real-time specification of the ionospheric conditions will increase in number, an ever more reliable and robust representation of the ionosphere will become of outstanding importance. This is why near real-time data-assimilation models such as IRTAM need continuous improvement and refining, on the one hand to improve the climatological description of the ionosphere made by IRI, and on the other hand to pave the way for a reliable ionospheric weather description.