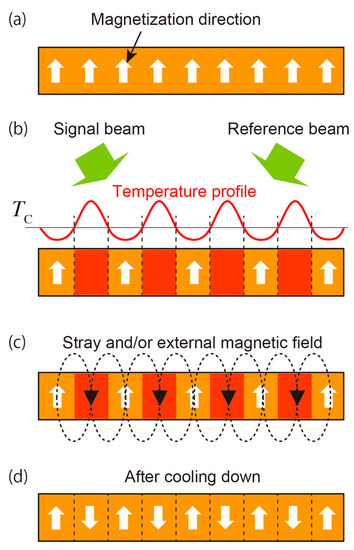
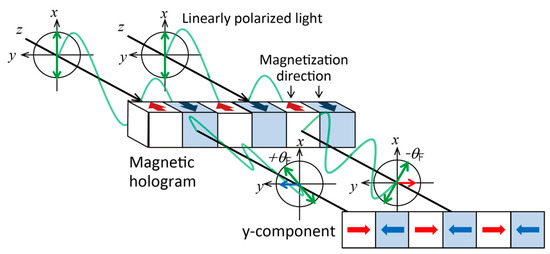
The magneto-optical effect is used for reconstruction of a magnetic hologram. The magneto-optical effect is a phenomenon in which the polarization plane rotates depending on the direction and strength of magnetization when linearly polarized light is incident on a magnetic material. The magneto-optical effect on transmitted light is called the Faraday effect, and that on reflected light is called the Kerr effect. schematically shows the reconstruction principle for transmitted light. When linearly polarized light is incident on the magnetic grating, the polarization plane rotates in the opposite direction depending on the direction of magnetization. At this time, when we see the component in the direction orthogonal to the polarization plane of incident light, the light has a phase difference of 180°. When the reference light is incident on the magnetic hologram, this component of the diffracted light interferes with each other, so that the signal light is reconstructed by the principle of the phase hologram
[21][22][23]. The S/N ratio of the reconstructed light can be improved, therefore, by separating only the component orthogonal to the incident light polarization plane, using the analyzer
[18].
Hascal
[23] discussed in detail the reconstruction principle and diffraction efficiency of magnetic holograms. In a binary magnetic hologram, the polarization plane of diffracted light is orthogonal to that of the incident light. On the other hand, in a magnetic hologram with magnetization distribution, such as a trigonometric function, an even order diffracted light, including the 0th order transparent light, has a polarization plane that is the same as that of the incident light, while the polarization plane of the odd order diffracted light is orthogonal to that of the incident light. In either case, the strength of the diffracted light of the second order or higher is sufficiently weak, so the first order diffraction light that has a polarized plane orthogonal to the incident light is used. Theoretically, the diffraction efficiency
η of the first-order diffracted light is described as follows:
with the rotation angle
θF of the magnetic hologram as
θF =
Ft, where
F is the Faraday rotation coefficient representing the rotation angle per unit thickness, and
t is the depth of the magnetic hologram, respectively. This diffraction efficiency
η is an index of the brightness of the reconstructed image, and a bright reconstructed image can be obtained by forming a deep volumetric magnetic hologram on the recording material with a large rotation angle per unit thickness. Equation (1) shows that the diffraction efficiency decreases when the Faraday rotation angle exceeds 90 degrees. However, for example, the Faraday rotation angle of a typical bismuth-substituted rare earth iron garnet is about several deg./µm at a wavelength of 532 nm, and, as will be described later, the recording depth by thermomagnetic recording is about 1 to 2 µm. On the other hand, magnetic metal films, such as MnBi, show a rotation angle of several tens of deg./µm, while the recording depth is only 100 nm or less due to large light absorption. Hence, we need not worry that the rotation angle becomes too large since the rotation angle of the magnetic hologram will be less than 10 degrees. Therefore, the recording conditions for recording the magnetic hologram as deeply as possible are desirable.
Tanaka et al.
[37] recorded interference fringes on the Bi–Mn film by the two-beam interference method and experimentally showed that the diffraction efficiency was proportional to the 2.3rd power of the Faraday rotation angle, which is in good agreement with the theory. In addition, Chen et al.
[35][38] recorded and reconstructed a two-dimensional dot pattern on the Bi–Mn film and proved that complex two-dimensional patterns can be recorded and constructed with magnetic holograms. Nakamura et al.
[25] reported that the diffraction efficiency of the magnetic fringe with 500 line-pair/mm was larger than that with 1500 line-pair/mm. The diffraction efficiency is theoretically independent of the fringe spacing, but the depth of the magnetic fringe with 500 line-pair/mm was deeper than that with 1500 line-pair/mm from the numerical simulation as mentioned in
Section 2.1. Therefore, this large diffraction efficiency was thought to be attributed to the deep magnetic fringe from Equation (1).
3. Conclusions
The principle of magnetic holography and the development of the magnetic hologram memory were reviewed. The magnetic hologram is recorded by the thermomagnetic recording method and reconstructed with the magneto-optical effect. Therefore, a bright reconstruction image is achieved by recording a deep magnetic hologram in the recording material with a large Faraday rotation coefficient. Although the first reconstruction image was dark and noisy, the improvement in the recording conditions resulted in error-free recording and reconstruction of the magnetic hologram. In addition, HD multilayer media were proposed to avoid the merging of the magnetic fringes and to form a deep magnetic hologram. The properly designed HD multilayer medium showed that the diffraction efficiency is larger than that of the usual single-layer film. Error-free recording and reconstruction were also achieved, using the magnetic assisted recording technique. This suggests that the HD multilayer media have potential applications in the recording media of magnetic holographic data storage and are suitable for volumetric hologram recording, which is advantageous for multiple recordings. In future, the development of a high recording density technique, such as multiple recording, is expected.