In any membrane filtration, the prediction of permeate flux is critical to calculate the membrane surface required, which is an essential parameter for scaling-up, equipment sizing, and cost determination. Permeate flux prediction is an essential parameter in membrane performance evaluation and the projections for scaling-up from laboratory to the pilot plant or the industrial scale.
1. Introduction
Membrane processes have become major techniques in the food industry over the last few decades, thanks to their ability to provide gentle treatment of products at low-to-moderate temperatures.
Membrane applications in the food industry have focused on separation, fractionation, purification, clarification, and concentration of several food products and by-products such as whey, milk, wine, beer, vinegar fruit, and vegetable juices
[1]. Typical advantages over conventional separation systems include high separation precision, better selectivity, operation at room temperature, no chemical damage, high automation, easy operation, energy saving, reduced cost, comprehensive utilization of resources, and reduced pollution. For these reasons, membrane processes are often recognized as the best available technology (BAT) in the food industry
[2][3][4]. Among pressure-driven membrane processes, ultrafiltration (UF) has been extensively applied in the treatment of industrial effluents
[5][6][7][8][9][10], oil-based emulsions
[11][12][13][14], biological macromolecules
[15][16][17], milk
[18][19][20], sugar cane
[21][22], extracts of soybean flour
[23], clay suspensions
[24], black kraft liquor
[25], and fruit juices
[26][27][28][29][30][31][32][33][34][35][36][37] among others. Within the fruit juice industry, bergamot, kiwifruit, and pomegranate have great importance in the market, not only for their volume of production, but also because they are characterized by a high concentration of phytochemicals which are recognized to be associated with antioxidant activities within others. Bergamot (Citrus bergamia, Risso) is an evergreen tree almost exclusively grown on the Ionian and Tyrrhenian Coast of Reggio Calabria Province (South Italy) with a production of 18,750 tons in 2017
[38], representing a significant economic benefit. Bergamot has been mainly cultivated to extract essential oils with applications in food, cosmetic and pharmaceutical industries
[39] because of their high content of phytochemicals such as flavanone glycosides, limonoids, and quaternary ammonium compounds, all health-beneficial biomolecules
[40][41]. On the other hand, Bergamot juice is considered a residue for its bitter taste; however, this juice is characterized by a large quantity and variety of nutraceuticals such as naringin, neoeriocitrin, neohesperidin, rutin, neodesmin, rhoifolin, and poncirin with demonstrated health implications
[26]. Kiwifruit is another fruit with a high content of phytonutrients, including carotenoids, lutein, phenolics, flavonoids, vitamin C, and chlorophyll, all of them with strong antioxidant activity
[31][32][33][42]; therefore, it offers benefits for specific health conditions and, consequently, it has a great potential for industrial exploitation. Italy, as the major producer worldwide, has a production of 330,000 tons/year (corresponding to 33% of the world production) principally in the regions of Latium, Emilia-Romagna, Piedmont, and Apulia
[32]. Pomegranate (
Punica granatum L.) is located in many different geographical regions, including tropical and subtropical regions. The leading producer locations include Mediterranean countries, India, Iran, and California
[43]. Since several authors reported the therapeutic benefits of its consumation including antioxidant, antimicrobial, anti-carcinogenic, and anti-inflammatory properties, increased interest has been garnered for this fruit
[44]. Polyphenolic compounds, including ellagotanins, anthocyanins, ellagic acid, and minerals, potassium, magnesium, and copper, are associated with a beneficial effect on health. The global pomegranate market was valued at USD 8.2 billion in 2018 and is expected to reach USD 23.14 billion by 2026 at a Compound Annual Growth Rate (CAGR) of 14.0 percent. Its widespread popularity drives increasing demand for pomegranate and its derivatives (such as pomegranate powder, pomegranate juice, functional beverages) as well as other pomegranate-derived products as a functional food and a source of nutraceuticals
[43].
Regarding membrane processes, permeate flux in UF is one of the most critical parameters for evaluating membrane performance. Indeed, the evaluation of permeate flux, usually expressed as volume (or weight) per unit membrane area per unit time, is a critical issue in the projection of scaling-up from experience at the laboratory scale to pilot or industrial plants for a specific volume treatment requirement
[45]. Thus, it is a crucial task to forecast permeate flux in long-term operations.
2. Theory
Regarding filtration, Carman
[46][47] was the first one to propose a relationship for an aggregate cake, where the prediction of permeate flux is related to the structure parameters of the cake layer, including mean particle size and thickness
[48]. This relationship is known as the Carman–Kozeny equation.
In a pressure-driven filtration process such as UF, the pure solvent flux (commonly water) through a porous membrane is directly proportional to the applied hydrostatic pressure, according to:
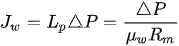
(1)
where Jw is the solvent permeate flux, ΔP is the transmembrane pressure, Lp is the membrane permeability, µw is the solvent viscosity, and Rm is the intrinsic membrane resistance.
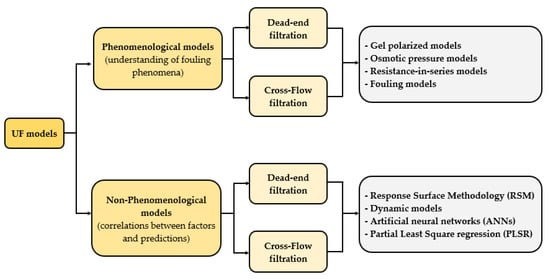
Figure 1. Classification of models developed for MF and UF processes.
3. Analysis of Model Goodness-of-Fit
The categories described previously comprised phenomenological, empirical, semi-empirical, and non-phenomenological models (e.g., statistical tools) developed between 1961 and 2019. In order to compare the capacity of permeate flux prediction, some models for each category were selected and tested with data of three fruit juices clarified by UF. The criteria used for the model selection include a series of items in the following order of importance:
- (i) Type of configuration: models tested or developed for cross-flow filtration of fruit juices were selected.
- (ii) Validation: models with more than one validation were considered.
- (iii) The number of citations: models with a high number of citations were selected in order to take into account the scientific impact of each model.
- (iv) Membrane module: models tested or developed in fruit juice processing with hollow fiber and tubular membranes were selected.
- (v) Mathematical complexity: Considering the easy application of the models, the most straightforward models were preferred.
Based on these criteria, the models selected were: Shear-induced diffusion by Davis
[49] for concentration polarization category; models described by Keden and Katchalsky
[50] and Wijmans et al.
[51] were selected for osmotic pressure; Hagen-Poiseuille and Boundary gel law described by De et al.
[52] were selected for the resistance-in-series category; models described by Ho and Zydney
[53], Mondal et al.
[54] and the dynamic model by Song
[55] were chosen for the fouling category; and models described by Yee et al.
[56] and Ruby-Figueroa et al.
[57] were selected within the non-phenomenological category. Simulations were performed using experimental data obtained in the UF of three different fruit juices processed for 10 h, as reported by Ruby-Figueroa et al.
[57] In , characteristics of the juices, membrane types, and operating conditions are reported. Variables such as viscosity, bulk concentration, permeate volume, osmotic pressure, the resistance of the polarized layer, gel concentration, and gel thickness were obtained using a series of correlations available in the literature.
Table 1. Description of the UF membrane, operating conditions, and physicochemical characteristics of the fruit juices analyzed in this work.
| |
Bergamot |
Kiwi Fruit |
Pomegranate |
Reference |
| DCQ II-006C |
Koch Series-Cor TM HFM 251 |
FUC 1582 |
| Membrane characteristics and operation |
|
|
|
|
| Membrane material |
Polysulfone (PS) |
Polyvinylidene fluoride (PVDF) |
Triacetate cellulose (CTA) |
- |
| Configuration |
Hollow Fiber |
Tubular |
Hollow Fiber |
- |
| Area (m2) |
0.16 |
0.23 |
0.26 |
- |
| MWCO (kDa) |
100 |
100 |
150 |
- |
| ΔP (bar) |
1 |
0.85 |
0.6 |
- |
| Temperature (°C) |
20 |
25 |
25 |
- |
| Flow (Lh−1) |
114 |
800 |
400 |
- |
| Porosity (dimensionless) |
0.0057 |
1.1 |
0.0007 |
|
| Tortuosity (dimensionless) |
3 |
3 |
0.03 |
- |
| Membrane thickness (m) |
4.7 × 10−7 |
2.0 × 10−6 |
0.00023 |
[34] |
Pore density, N
(number of pores m−1) |
6.0 × 1012 |
4.0 × 1016 |
1.0 × 1013 |
[58] |
| Module length, L (mm) |
330 |
406 |
136 |
[59] |
| Module diameter (m) |
0.0021 |
0.025 |
0.0008 |
[30][58][60] |
| Hydraulic resistance (m−1) |
3.6 × 1012 |
1.6 × 1012 |
2.1 × 1012 |
- |
| Hydraulic permeability (mPa−1s−1) |
2.7 × 10−10 |
5.9 × 10−10 |
4.6 × 10−10 |
- |
| Fruit juices characteristics |
|
|
|
|
| Total soluble solids (°Brix) |
9.4 |
12.6 |
18.7 |
[30][38][43][61] |
| Titratable Acidity |
53.86 (gL−1) |
- |
1.04 (% citric acid) |
[30][38][43][61] |
| pH |
2.40 |
3.19 |
3.61 |
[30][38][43][61] |
| Total phenolic compounds |
660 (mg/L) |
421.6 (mg/L) |
1930 (mg GAE/100 L) |
[30][38][43][61] |
| Turbidity (%) |
33.67 |
- |
|
[30][38][43][61] |
| Feed density, ρ (kgm−3) |
1091 |
1070 |
1131 |
[62][63] |
| Feed viscosity, μ (Pa s) |
0.0019 |
0.0014 |
0.0017 |
[31][64] |
| Concentration in food (%) |
12 |
10.08 |
4.9 |
[27][33][36] |
The determination of the quality of fit for the selected models was performed using the root mean square error (RMSE), the mean absolute percentage error (MAPE), and the percentage of variability explained (R2) at 95% confidence level. In addition, a validation procedure was carried out using residual analysis. The analysis of residuals, intended as the difference between the observed and predicted value, is fundamental for validating any model. The residuals represent the prediction error: they must have a random distribution and they must be unpredictable, which means that they must follow a normal distribution. In cases where the residuals do not have a normal distribution, the constants and predictors included in the model are intended not to be enough to predict the response. In this sense, two statistics, such as the Shapiro–Wilks (S-W) and Kolmogorov–Smirnov tests (KS), were used for determining the normal distribution of the residues for the analyzed models. Thus, it is expected that a valid model must demonstrate a normal distribution in at least one of the statistics used. All the computations were performed in Statgraphics Centurion XVI (Statgraphics Technologies, The Plains, VA, USA) and Excel 2010 (Microsoft, Redmond, WA, USA).
Results of statistically validated models showed high variability in the prediction capacity by phenomenological models for the studied juices. In particular, phenomenological models present a capacity of prediction ranging from 75.91 to 99.78% (R-squares), whereas the Mean Absolute Percentage Error (MAPE) ranged from 3.14 to 51.69, and Root Mean Square Error (RMSE) from 0.22 to 2.01. Non-phenomenological models showed a better prediction of permeate flux with R-squares higher than 97% and lowered MAPE (0.25–2.03) and RMSE (3.74–28.91) in comparison with phenomenological models. However, these models do not provide information related to the effect of different parameters on the permeate flux, a crucial point for the system scaling-up. On the contrary, phenomenological models are still a proper method for scaling-up purposes, mainly for research in the understanding of the UF process. Therefore, the challenge herein is the development of new phenomenological models with assumptions that include the different phenomena occurring in the filtration of complex matrices in order to improve the capacity of prediction of permeate flux in long-term operation.