
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Charles Roberto Telles | + 565 word(s) | 565 | 2019-01-04 13:51:14 | | | |
| 2 | Charles Roberto Telles | + 585 word(s) | 585 | 2019-01-04 17:15:16 | | | | |
| 3 | Charles Roberto Telles | + 588 word(s) | 588 | 2019-01-04 20:10:26 | | | | |
| 4 | Charles Roberto Telles | + 600 word(s) | 600 | 2019-01-04 20:13:48 | | | | |
| 5 | Peter Tang | -19 word(s) | 581 | 2020-11-01 10:41:56 | | | | |
| 6 | Peter Tang | -19 word(s) | 581 | 2020-11-01 10:46:10 | | |
Video Upload Options
The main purpose is to identify among variables that constitute water resources consumption at public schools, the link between consumption and expenditures oscillations. It was obtained a theoretical model of how oscillations patterns are originated and how time lengths have an important role over expenditures oscillations ergodicity and non-ergodicity.
1. General Description
For better measurement of oscillation behavior regarding ergodicity properties of any expenditure system, it is possible to obtain an optimal solution of how the variables that promotes the event behave[1].
It is considered that oscillations can be caused by random variables or unstable administration of management agents. In both cases, a monitoring method is mandatory for prediction purposes and optimization of variable expressions[2].
Despite random effects in large expenditure systems are normal events, it is expected periodic oscillations to occur due to weighted PDF that compose any event in social and economic structure. These features reveal a pre-deterministic condition in which expenditures should follow strictly caused as an attractor of these PDF functions. But in opposite hand it does not happen for any given system of events in a natural way. For this reason, for the natural processes that promote system instability, theory of information could lead a possible way to track the flow and cause of oscillations, giving the possibility of understanding how in high dimensional events, micro flows of variables affect the macro flows with direct causal relations (figure 1)[3][4][5][6].
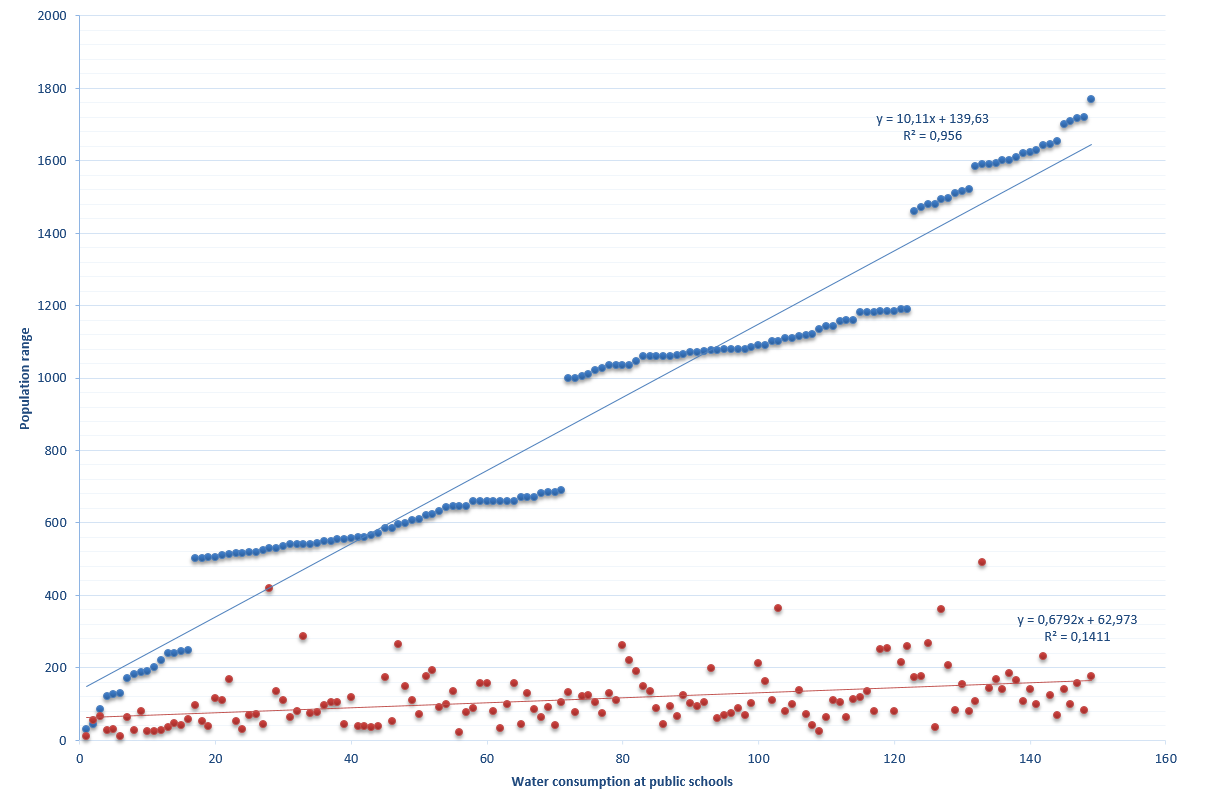
Figure 1. Water usage at public schools. The data consist of 149 schools at different regions of the Paraná State with a population of individuals. Using R2 (determination coefficient) for both data, the linear function presented for the chosen population data can’t be equally found in the water usage behavior[2].
In figure 1, it is observed how public schools consume water where the amount of the school’s population has very slight influence on it. From 100 to 1700 population, the ratio of water consumed is not given by an average consume indicating a nonlinear event, therefore, non ergodic properties of an expenditure system[2].
By tracking population and resources expression aspects, it is observed that the ratio of resources consumes follows in this case a specific behavior regulated by time lengths in which PDF can be controlled disregarding the quantitative aspect of variables, but mainly by timing aspect of the event (figure 2)[7][8][9].
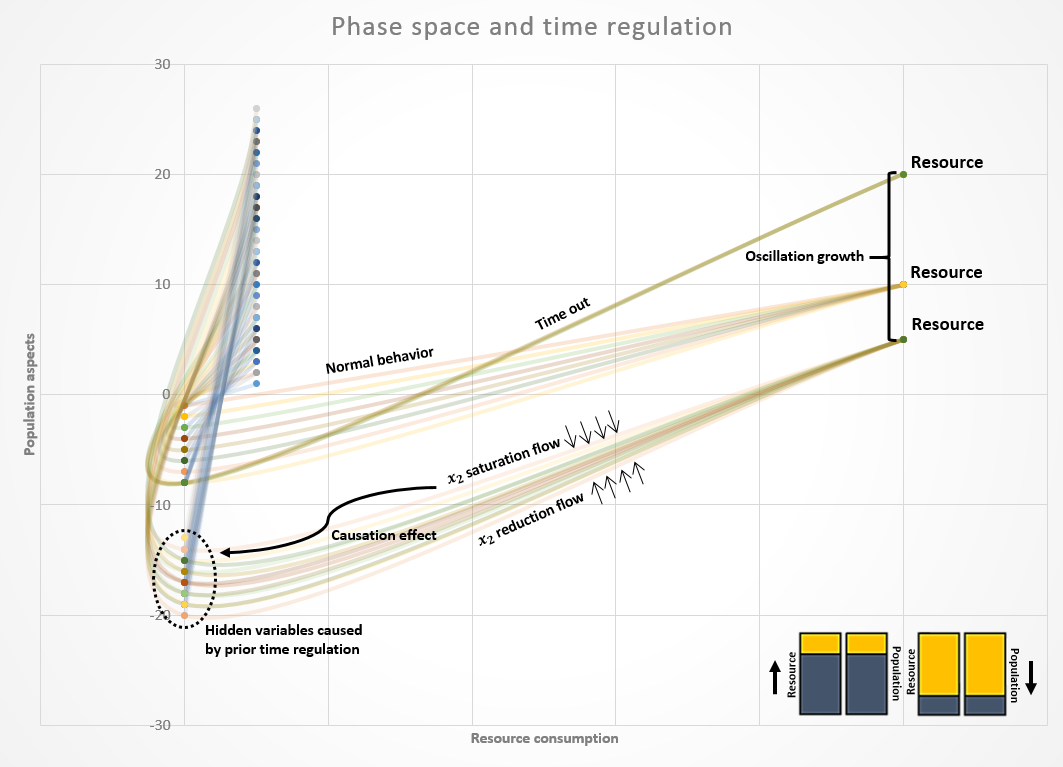
Figure 2. Deterministic to chaotic behavior of variables regulated by time lengths. Observation: the lines are colored for the benefit of graph visualization.
2. Conclusion
One conclusion arising from article experiment is to demonstrate how non-ergodicity of variables that compose water consumption (microstructure) at schools is responsible for non-ergodic oscillations in water expenditures (macrostructure). The information flow found in water consumption at schools is very high in terms of interactions, iterations, frequency of iterations, and time expressions. These properties lead to a high level of oscillations in water usage, leading as well to an unstable degree of water consume from each one of the 2000 public schools. As a symmetric result, the instability that is produced in water usage reflects with instability of expenditures observed for all the public provision of service. This relation was discussed as a possibility of using these type of analysis as a tool (indicator) for managers in order to be able to infer in complex systems of expenditures, how to reduce unwanted effects, such as continuous growth of expenditures, chaotic behavior of the system, uncertainty and summarizing it, very suboptimal public administration, and the use of tax money.
The entry is from 10.3390/sym10110645
References
- Elizabeth Anne Eppel; Mary Lee Rhodes; Complexity theory and public management: a ‘becoming’ field. Public Management Review 2017, 20, 949-959, 10.1080/14719037.2017.1364414.
- Charles Roberto Telles; Andrea Regina Burakoski Da Cunha; Ana Maria Sawaya Chueiri; Kamila Kuromiya; Analysis of oscillations in continuous expenditures and their multiple causalities: a case study. Journal of Economic and Administrative Sciences 2018, 34, Early publication, 10.1108/jeas-06-2018-0073.
- Dimitris Bertsimas; Aurélie Thiele; Robust and Data-Driven Optimization: Modern Decision Making Under Uncertainty. Models, Methods, and Applications for Innovative Decision Making 2006, 1, 95-122, 10.1287/educ.1063.0022.
- Subhes C. Bhattacharyya; Govinda R. Timilsina; Energy Demand Models For Policy Formulation: A Comparative Study Of Energy Demand Models. The Limits of Commitment: Who Benefits From Illiquid Savings Products? 2009, 1, 151, 10.1596/1813-9450-4866.
- Terje Aven; Risk assessment and risk management: Review of recent advances on their foundation. European Journal of Operational Research 2016, 253, 1-13, 10.1016/j.ejor.2015.12.023.
- Uzi Harush; Baruch Barzel; Dynamic patterns of information flow in complex networks. Nature Communications 2017, 8, 2181, 10.1038/s41467-017-01916-3.
- Kevin Knuth; Deniz Gençağa; William Rossow; A Recipe for the Estimation of Information Flow in a Dynamical System. Entropy 2015, 17, 438-470, 10.3390/e17010438.
- Charles Roberto Telles; Geometrical Information Flow Regulated by Time Lengths: An Initial Approach. Symmetry 2018, 10, 645, 10.3390/sym10110645.
- Reik V. Donner; Michael Small; Jonathan Donges; Norbert Marwan; Yong Zou; Ruoxi Xiang; Jürgen Kurths; RECURRENCE-BASED TIME SERIES ANALYSIS BY MEANS OF COMPLEX NETWORK METHODS. International Journal of Bifurcation and Chaos 2011, 21, 1019-1046, 10.1142/s0218127411029021.




