1000/1000
Hot
Most Recent
This video is adapted from 10.3390/e23121666
Qualitative theories of various processes and phenomena are constructed on the basis of topological invariants. Theories of this type allow identifing characteristic properties of a group of objects and predict the behavior of the system. The use of qualitative methods makes it possible to move from the study of individual processes (phenomena) to their equivalence classifications.
Phase equilibrium diagrams are characterized by topological invariants, on the basis of which equivalence classifications are created, properties of unexplored objects are predicted. A number of topological invariants of vapor-liquid, vapor-liquid-liquid and liquid-liquid equilibrium diagrams are considered [1]: Euler characteristic and the balance rule for singular point indexes; The balance of the indices of the singular points participating in the bifurcation; Euler characteristic as an alternative sum of elements of different dimensions; Poincare integral invariant and separatric manifolds; Invariant of the liquid-liquid equilibrium diagram; Invariant of the splitting region.
I) Euler characteristic and the balance rule for singular point indexes
The azeotropy rule[2] based on the Euler characteristic is invariant with respect to vapor-liquid equilibrium diagrams of systems with any number of components. Two forms of this rule are known, suggested by Gurikov[3] and Zharov: ![]()
and by Serafimov[4] :
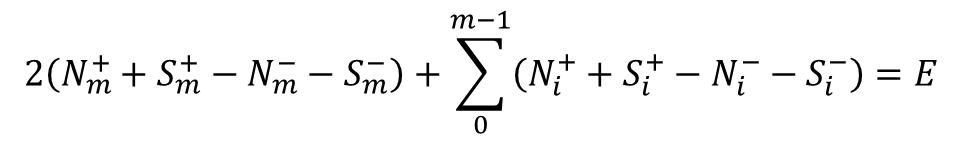
where E – Euler characteristic determined by the equation, m – the dimension of the element on which the singular point is located, "+" and "-" correspond to the sign of the Poincare index of the singular point.
For ternary systems, both equations can be reduced to the following form (proposed by Gurikov):
![]()
A complete atlas of VLE diagrams of ternary systems and an equivalence classification was developed was obtained based on the solution of the this equation[5].
The index balance equation applies not only to the complete phase but also to its elements (for example, separatrix surfaces).
An analogue of the one previously considered is an equation connecting elliptic and hyperbolic points on the surface of any scalar property [6]:
![]()
An example of the relationship between elliptical and hyperbolic points of the equilibrium temperature surface is shown in Figure 1

Figure 1. Elliptical and hyperbolic points on the surface of equilibrium temperatures
2) The balance of the indices of the singular points participating in the bifurcation
The sum of the Poincare indices of the singular points participating in the bifurcation is a constant value[2]. Figure 2 shows an example of bifurcation of the diagram through the stage of formation of a boundary double tangential azeotrope (two binary azeotropes merge at the vertex of the composition triangle, followed by the formation of a ternary azeotrop from this vertex).
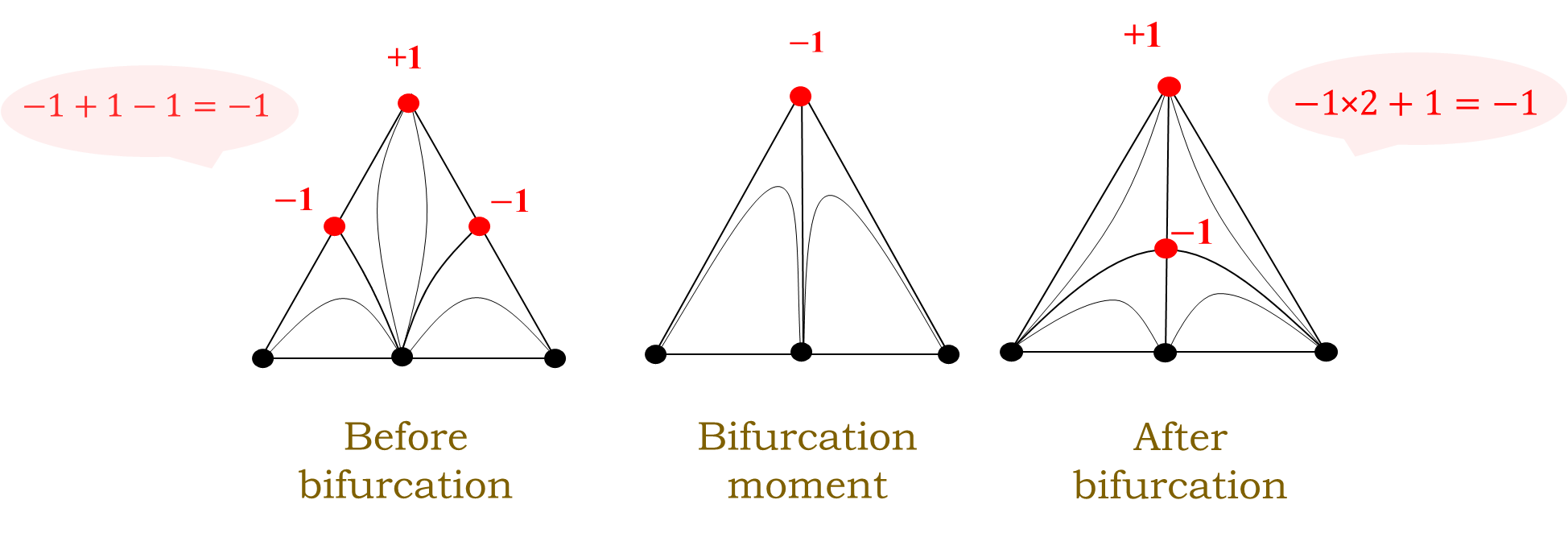
Figure 2. An example of the bifurcation of the VLE diagram through the stage of formation of a boundary double tangential azeotrope
3) Euler characteristic as an alternative sum of elements of different dimensions
Euler characteristic for manifold with boundary can be determined as
![]()
where – an element of a manifold of dimension m.
The phase diagram is characterized by a simplicial structure. For any simplex, the Euler characteristic is always equal to 1. Regardless of how many manifolds of different dimensions are present in the system (azeotropes, separatrix surfaces), the Euler characteristic of the diagram will not change (Figure 3)[1].

Figure 3. An example of determining the Euler characteristic as the sum of elements of different dimensions for the diagrams of a ternary and quaternary system
4) Poincare integral invariant and separatric manifolds
Analysis of the VLE diagrams of systems with more than three components, in particular the internal separatrix surfaces contained in them, showed that the latter have properties in common with the Poincare integral invariant: the presence of a subspace of smaller dimension in l-dimensional space; the presence of a certain structure of the subspace; its closure[7]. The relationship between the separatrix manyfold and the integral Poincare invariant allowed clarifing the concept of «multicomponence» of the system. Multicomponent should be called systems with a number of components from four and above. This suggests that ternary systems are only a transitional link between binary and multicomponent, that is manifested in the specifics of phase behavior.
5) Invariant of the liquid-liquid equilibrium diagram
The boundary space of the phase diagram is homeomorphic to a sphere of the corresponding dimension.The miscibility area is "cut out" from the diagram boundary space (Figure 4)[1].
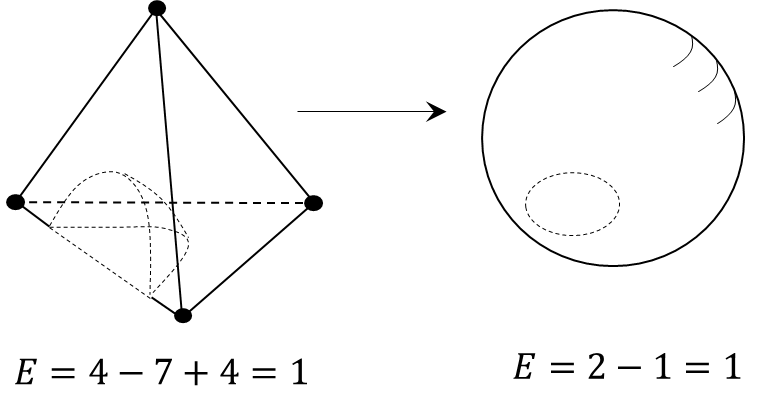
Figure 4. An example of mapping the boundary space of a composition tetrahedron to a sphere of the second dimension
Consequently, a “hole" will appear on the sphere and its Euler characteristic will decrease by the number of such holes (d) [8]:
![]()
An equation is an invariant of the LLE diagram describing its boundary space.
6) Invariant of the splitting region
The sum of the number of degrees of freedom in the liquid-phase splitting region and the phase simplex dimension is a constant value[9]:
![]()
where R is the dimension of the liquid phase splitting simplex (always one less than the number of liquid phases), n - number of components in the system, f - this is the number of degrees of an open chemically inert system determined in accordance with the Gibbs phase rule.
Some of the considered invariants formed the basis for the equivalence classification of phase diagrams development. The considered invariants are peculiar not only to the presented liquid-vapor, liquid-liquid, liquid-liquid-vapor equilibrium diagrams. For example, the balance equation of the indices of singular points is applicable to liquid-solid equilibrium diagrams[10][11][12].