1000/1000
Hot
Most Recent
This video is adapted from 10.3390/math9182253
A shape of geological discontinuities plays an important role in influencing the stability of rock masses. Many approaches have been used for its determination. The method of Barton and Choubey 1977 [1] is well known in geotechnical practice. A visual comparison is preferred way for determining values in geotechnical practice. A quick and easy estimate is probably one of the main reasons for this preference. However, this method is very subjective. Therefore, objective methods for estimation are searched. Most of them are based on measurement of diference between fracture surface and an appropriate reference surface. This contribution shows which reference surface is the right one.
Two height characteristics of the 3D profiles are obviously introduced as numerical indicators of a "distance" between surface 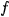 f to be study and the reference surface
f to be study and the reference surface  :
:
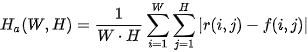

where 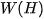 is the surface width (height) in pixels. From a statistical point of view, is the average distance of and , is the standard deviation. From a functional analysis point of view, these expressions are the distances of these surfaces in Manhattan (
is the surface width (height) in pixels. From a statistical point of view, is the average distance of and , is the standard deviation. From a functional analysis point of view, these expressions are the distances of these surfaces in Manhattan ( ) or Euclidean (
) or Euclidean (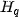 ) metrics. The question is how to construct a reference surface.
) metrics. The question is how to construct a reference surface.
Reference surface can be construct as a linear combination of monomials in two variables 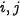 , i.e. as a standard polynomial in two variables
, i.e. as a standard polynomial in two variables 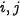 , i. e.
, i. e. 
using by least squares method. However, polynomial relatively high degree of polynomial is necessary for useable reference surface. This problem leads to a large system of linear equation. It is badly conditioned because monomial base is “very non-orthogonal” and solution is unuseable – see Figure 1.

Figure 1. Fracture surface (on the left) and its “reference approximation” constructed as standard polynomial of 19th degree.
The scanned relief  ; for
; for  and
and  is possible to expand into Fourier partial sums
is possible to expand into Fourier partial sums  (Standard Fourier sum) combining both the sine and cosine harmonics
(Standard Fourier sum) combining both the sine and cosine harmonics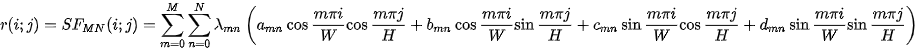
where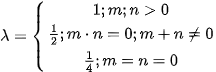
and

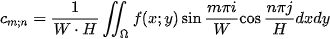
 where
where 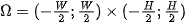
is a ground plan of the scanned relief [2].
This base is orthogonal and it is not necessary to solve any equation system. It means it is relatively easy to find very long expansion. However, there is an other problem.
Theorem (Dirichlet): The Fourier series  of a piecewise continuous function
of a piecewise continuous function 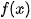 on interval
on interval  converges to the arithmetic mean of left-hand and right-hand limits of
converges to the arithmetic mean of left-hand and right-hand limits of 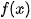 for
for  ; i. e.
; i. e. 
If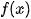 is discontinuous in
is discontinuous in  then
then  and
and converges to the arithmetic mean of these limits (convergence in the mean). If is continuous in
converges to the arithmetic mean of these limits (convergence in the mean). If is continuous in  then
then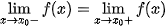 and
and  converges to the
converges to the 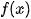 in
in  In the case of 2D by analogy.
In the case of 2D by analogy.
The Fourier series converges in the same way to periodic extension of  on
on  . The periodic extension of continuous fracture surface which is expanded to
. The periodic extension of continuous fracture surface which is expanded to  (odd extension) is generally not continuous. In Figure 2 on the left, we can see the periodic extension of function
(odd extension) is generally not continuous. In Figure 2 on the left, we can see the periodic extension of function 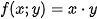 defined on
defined on 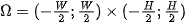 . Due discontinuities on the surface boundary,
. Due discontinuities on the surface boundary, 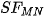 does not converge to surface points here, but to the arithmetic mean of opposite boundary points (so-called convergence in the mean).
does not converge to surface points here, but to the arithmetic mean of opposite boundary points (so-called convergence in the mean).

Figure 2. Different periodic extensions of the profile to be expanded (red perimeter). Left – discontinuous odd extension by 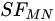 ; Right – continuous even extension by
; Right – continuous even extension by 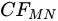 .
.
The scanned relief 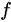 ; for
; for  and
and  is possible to expand into cosine Fourier partial sums
is possible to expand into cosine Fourier partial sums 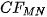 defined as follows:
defined as follows: 
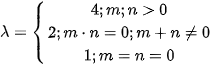

where 
is a ground plan of the scanned relief [3].
Periodic extension of continuous fracture surface which is expanded to 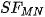 is discontinuous (see Figure 2 on the left). It means it suffers from convergence in the mean (se above) and also by so called Gibbs effect, i. e. by ”fake waves” nearby discontinuities. Periodic extension of continuous fracture surface which is expanded to
is discontinuous (see Figure 2 on the left). It means it suffers from convergence in the mean (se above) and also by so called Gibbs effect, i. e. by ”fake waves” nearby discontinuities. Periodic extension of continuous fracture surface which is expanded to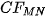 is always continuous (see Figure 2 on the right). Therefore, it does not suffer from these defects. In Figure 3, comparing the
is always continuous (see Figure 2 on the right). Therefore, it does not suffer from these defects. In Figure 3, comparing the 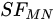 and
and 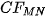 of the same “profile” - function
of the same “profile” - function  .
.

Figure 3. “Original profile” modelled by the function 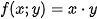 (in the middle) was expanded by
(in the middle) was expanded by 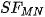 (on the left) and by
(on the left) and by 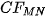 (on the right) in both cases.
(on the right) in both cases.
In Figure 4, expansion by 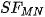 for real surface. Convergence in the mean and also Gibbs effect are evident in this case.
for real surface. Convergence in the mean and also Gibbs effect are evident in this case.
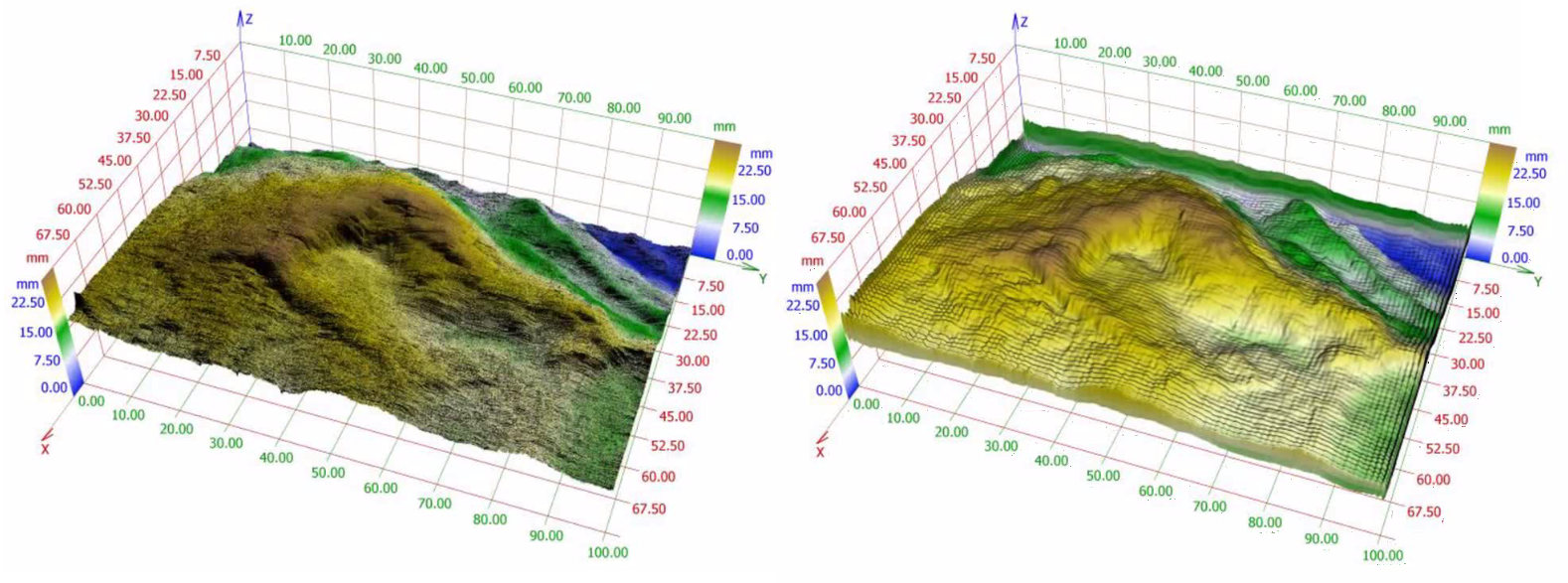
Figure 4. Aproximation of a real profile (on the left) by 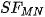 (on the right).
(on the right).
Figure 5 illustrate expansion by 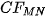 . It has no defects. For
. It has no defects. For 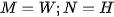 , the
, the 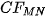 goes precisely through the surface points.
goes precisely through the surface points.

Figure 5. Aproximation of a real profile with resolution  (on the left) by
(on the left) by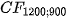 (on the right).
(on the right).