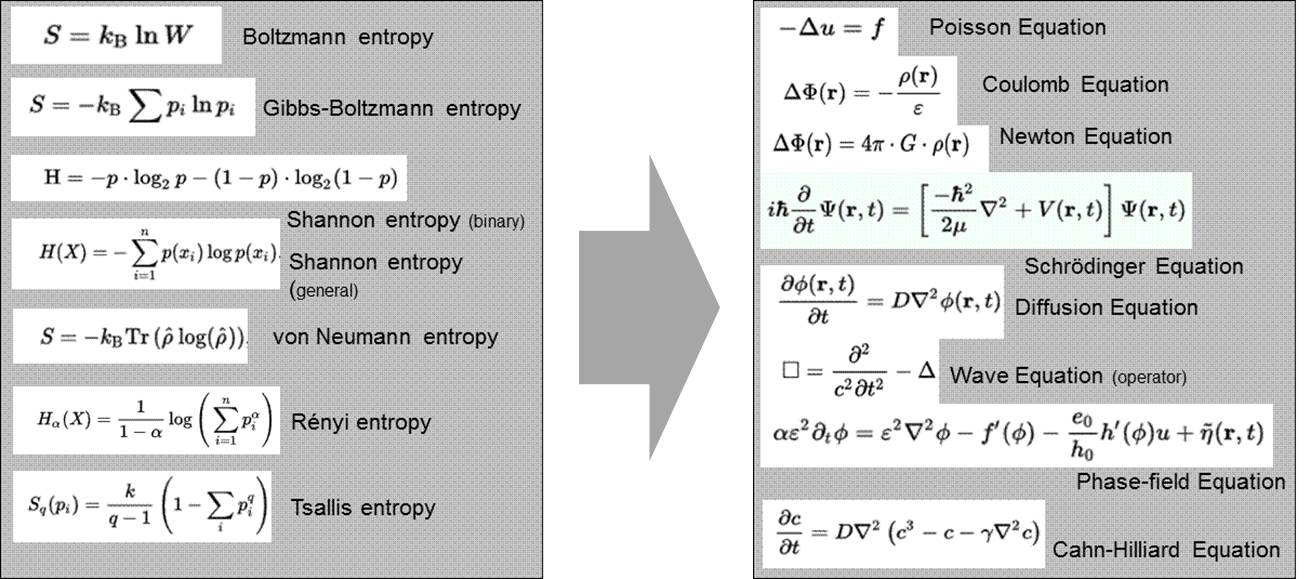
Different notions of entropy can be identified in different scientific communities: (i) the thermodynamic sense; (ii) the information sense; (iii) the statistical sense; (iv) the disorder sense; and (v) the homogeneity sense. Especially the “disorder sense” and the “homogeneity sense” relate to and require the notion of space and time. One of the few prominent examples relating entropy to both geometry and space is the Bekenstein-Hawking entropy of a Black Hole. Although this was developed for describing a physical object—a black hole—having a mass, a momentum, a temperature, an electrical charge, etc., absolutely no information about this object’s attributes can ultimately be found in the final formulation. In contrast, the Bekenstein-Hawking entropy in its dimensionless form is a positive quantity only comprising geometric attributes such as an area A—the area of the event horizon of the black hole, a length LP—the Planck length, and a factor 1/4. A purely geometric approach to this formulation will be presented here ^[1]. The approach is based on a continuous 3D extension of the Heaviside function which draws on the phase-field concept of diffuse interfaces. Entropy enters into the local and statistical description of contrast or gradient distributions in the transition region of the extended Heaviside function definition. The structure of the Bekenstein-Hawking formulation is ultimately derived for a geometric sphere based solely on geometric-statistical considerations.

The key ingredient to the approach is a statistical description of the transition region in a Heaviside or a phase-field function. For this purpose, gradients are introduced in the form of scalar products into the formulation of entropy based on the Temkin entropy of a diffuse interface. This introduces a length scale into entropy and provides a link between the world of entropy type models and the world of Laplacian type models:

The major claims of the presented concept are: