Multicore Fiber Interferometric Sensors: History
View Latest Version
Please note this is an old version of this entry, which may differ significantly from the current revision.
Contributor:
Yucheng Yao
,
Zhiyong Zhao
,
Ming Tang

Due to the specificity of fiber structure, i.e., multiple cores integrated into only one fiber cladding, multicore fiber (MCF) interferometric sensors exhibit many desirable characteristics compared with traditional fiber interferometric sensors based on single-core fibers, such as structural and functional diversity, high integration, space-division multiplexing capacity, etc. Thanks to the unique advantages, e.g., simple fabrication, compact size, and good robustness, MCF interferometric sensors have been developed to measure various physical and chemical parameters such as temperature, strain, curvature, refractive index, vibration, flow, torsion, etc., among which the extraordinary vector-bending sensing has also been extensively studied by making use of the differential responses between different cores of MCFs.

  • optical fiber sensors
  • multicore fiber (MCF)
  • Fabry–Perot interferometer (FPI)
  • Michelson interferometer (MI)
  • Mach–Zehnder interferometer (MZI)
  • supermode interferometer (SMI)

1. Introduction

Fiber interferometric sensors have basically the same operating principle as traditional optical interferometers. By replacing traditional discrete optical components with fiber devices, a fiber interferometer can achieve many benefits, including easy alignment, low insert loss, convenient arrangement, high stability, high coupling efficiency, etc. In fiber interferometer systems, the light travels along different optical paths and combines again at the output side, which generates an interference spectrum. External perturbations that are applied to the interference arms may cause property variations of the interferometer, including fiber length, effective refractive index, mode loss, etc., eventually leading to a change in optical path difference (OPD) or optical intensity. The change in OPD and intensity can be precisely retrieved by measuring the far-field interferogram [1][2], the wavelength shift of the interference spectrum [3][4], the light intensity [5][6], the fast Fourier transform (FFT) of light power’s time response [7][8], etc.
Apparently, compactness, stability, simplicity, and robustness play a decisive role in the performance and applicability of optical fiber sensing systems, and these aspects can be improved by using multicore fibers instead of single-core fibers to construct fiber interferometers. Benefiting from containing multiple individual cores in one fiber, MCFs can support the multiple cavities of the FPI, the multiple interference arms of the MI and MZI, and several supermodes in one fiber cladding, which can greatly simplify the structures of sensors and enhance the robustness and compactness of the sensing systems. On the other hand, since the side cores are usually more sensitive to external disturbances, MCF interferometric sensors have intrinsic advantages in sensing applications that are related to bending and strain, e.g., curvature [3][9], vibration [8][10], twisting angle [11][12], fluid flow [9][13], etc. Particularly, MCF interferometric sensors are able to distinguish the direction of bending [5][14], which has enabled many new sensing applications, e.g., 3D shapes [15]. In addition, MCF interferometric sensors have also been used to measure other external environmental parameters, e.g., temperature [16][17], gas concentration [18], refractive index [19][20], and so on.
The following sections will summarize different MCF interferometric sensor structures that are commonly used in fiber optic sensing, including their configurations, operating principles, and representative studies, as well as the benefits brought by MCFs.

2. MCF-Based Fabry–Perot Interferometric Sensors

As shown in Figure 1, Fabry–Perot interferometers (FPIs) can be classified into intrinsic FPIs and extrinsic FPIs according to the formation of the interference cavity. In the intrinsic FPI, the interference cavity is fabricated inside the optical fiber, while in the extrinsic FPI, a microcavity is fabricated between the cleaved optical fiber end and another external reflection surface. In comparison, the intrinsic FPI is generally more robust but requires more high-cost fabrication methods, such as femtosecond laser processing, chemical etching, external fixation using capillaries, etc.
Figure 1. Schematic diagram of (a) an intrinsic FPI and (b) an extrinsic FPI.
In the FPI, the reflective optical interference intensity can be expressed as
I = I 1 + I 2 + 2 I 1 I 2 cos φ
where I1 and I2 are the intensities of the reflective light from two interfaces, and φ is the phase difference between the two reflective lights, which can be defined as
φ = 4 π n L λ
where λ is the wavelength of the light source, L is the length of the cavity, and n is the refractive index of the medium in the cavity. The free spectrum range (FSR) at wavelength λ is given by
F S R = λ 2 2 n L
One can see from Equation (3) that bending/strain-induced cavity length L variation and environmental-perturbations-induced refractive index n changes will lead to a shift in the optical interference spectrum, which can be used to retrieve the perturbation of the parameters.
In MCF-based Fabry–Perot interferometric sensors, FPIs are usually discrete and parallel in different cores of a weakly coupled MCF [3][4][21][22][23][24]. Instead of using a single FPI, it is able to achieve vector sensing by measuring several parallel FPIs simultaneously in a single MCF, such as bending direction [3][21], torsion [22], flow direction [23], etc. 
In addition to bending sensing, parallel FPIs can also be used to measure tiny torsion angles by utilizing the twist-induced cavity length variation. For example, in 2022, Jing Zhang et al. proposed a torsion sensor where four FPIs were made up of vertically cleaved four-core fibers and an angled mirror, and the sensor was demonstrated to be capable of sensing torsion with a range of ±90° and a resolution of 0.01° [22]. As shown in Figure 2, the cavity length of each FPI will change, respectively, when torsion is applied to the four-core fiber and the spectral characteristics of each FPI can be analyzed utilizing a four-core fan-out unit.
Sensors 23 03436 g005 550
Figure 2. Schematic of the torsion sensor based on FPIs made up of a 4-core fiber [22].
Furthermore, in addition to bending and torsion sensing, MCF Fabry–Perot interferometer (MFPI)-based sensors can also be used for axial displacement sensing by changing the distance between the two reflective surfaces of FPIs. By fabricating reference and sensing FPIs in a single MCF, a compact sensor head can be achieved. In general, due to the compact reflective structure, heat resistance, corrosion resistance, and high electromagnetic immunity, MFPI-based sensors can be easily deployed in complex actual environments for a variety of sensing applications.

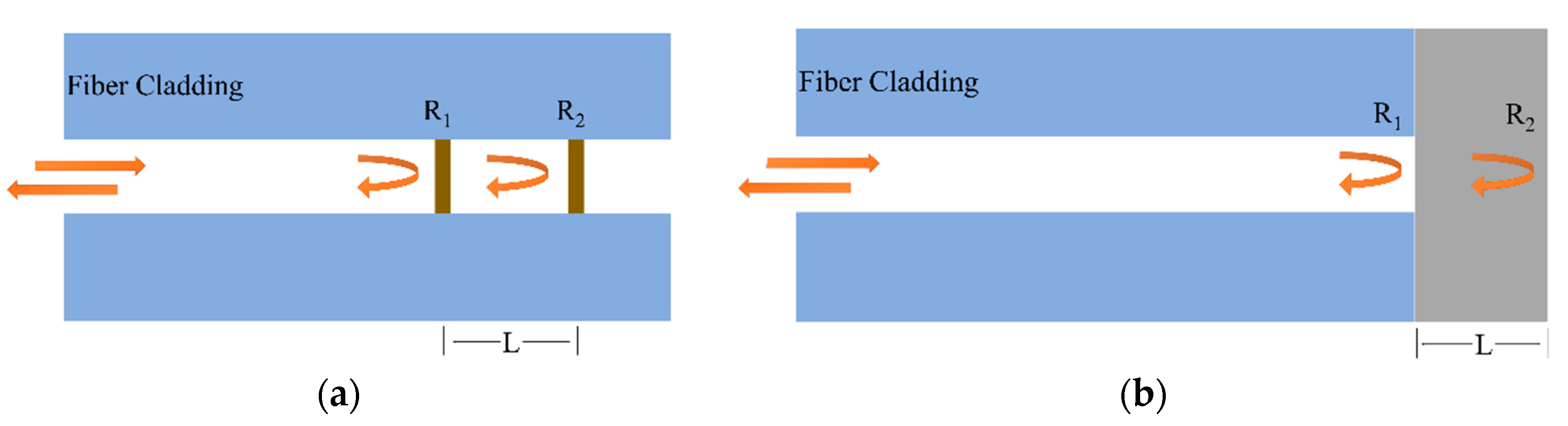
3. MCF-Based Michelson Interferometric Sensors

Thanks to the multicore structure of MCF, it provides an excellent platform to construct an in-fiber integrated Michelson interferometer by coupling light into different cores so that the cores act as the arms of the Michelson interferometer. Fresnel reflection light is generated on the end face of the cleaved optical fiber, and the reflected light from different cores of the MCF will give rise to interference. Typical coupling methods of MCF-based Michelson interferometers (MMI) are shown in Figure 3. Instead of using fiber couplers, in order to couple light into different cores of an MCF, the widely used approaches including tapering the fiber at the fusion splice region [9][13][25][26][27] or inserting a segment of multimode fiber (MMF) between the single-mode fiber (SMF) and MCFs [28]. These coupling methods have the advantages of compact structure and long-term stability because of the good spatial consistency of the interference arms. Note that by enhancing the coupling efficiency between fiber cores, e.g., the center core and side cores of the MCF, the light power in each interference arm can be more even and the fringe visibility of the interference spectrum can be improved, which is instrumental in the simplicity of demodulation and the accuracy of measurement.
Sensors 23 03436 g007 550
Figure 3. Schematics of typical coupling methods of the MCF-based Michelson interferometer. (a) Tapering the MCFs at the fusing point, (b) fusing a segment of MMF between the SMF and MCFs.
In addition to the method of tapering, to optimize the interference spectrum quality of the MMI, coupling configurations based on a fiber ball structure have been demonstrated, which have been fabricated on the fusion surface [29] and the reflecting surface [16]. In 2016, Li Duan et al. demonstrated an MMI temperature sensor by tapering the fusion-spliced region between the SMF and the MCF and fabricating a spherical end face by arc-fusion splicing. The first coupling appears when the light transmits through the tapered region and the second coupling occurs at the spherical end face when the light is reflected. The light power of the side cores and the center core can be balanced at the spherical end face and, as a result, a high fringe visibility of 25 dB was achieved, which is more than 10 dB higher than the normal MCF-based Michelson interferometers [25][26][27][30].
In the MMI, the phase difference φ of reflected light from two cores is governed by
φ = 2 π · O P D λ
where OPD is given by
OPD = 2 n 1 L 1 − n 2 L 2
where n1 and n2 are the refractive indexes of the two optical fiber arms, while L1 and L2 are the lengths of different arms. The intensity of the interference spectrum is minimal when
φ = 2 m + 1   π
and the wavelength of the dip is determined by
λ m = 2 · O P D 2 m + 1
Thus, the FSR of the Michelson interferometer can be expressed as
FSR = λ m − 1 − λ m ≅ λ m 2 O P D = 4 · OPD 2 m + 1 2
Compared with the FPI, the FSR of a Michelson interferometer is determined by the OPD of the two arms rather than the length of a single interference cavity. Therefore, by precisely controlling the length difference between the two arms, the Michelson interferometer can achieve a large FSR while allowing for long sensing arm length. For the wavelength demodulation-based interrogation system, the Michelson interferometer can achieve a large dynamic sensing range without sacrificing the length of the sensor, which can affect the performance in terms of bending/strain sensitivity and resolution. However, due to the short coherence length of the broadband light source, the OPD between different arms needs to be strictly controlled in a small range in order to generate interference, which increases the fabrication complexity of the Michelson interferometer. Fortunately, due to the almost identical optical path length of each core of MCF, an in-fiber integrated Michelson interferometer using MCF is capable of solving this problem perfectly, which allows for long interference arms and controllable OPD simultaneously. When bending is applied to the MMI, according to the photo-elastic effect, the variation in phase difference Δφ can be described as 
Δ φ = 2 π λ n Δ L + Δ n L = 2 π L λ n + n d n d ε Δ ε
where ΔL and Δn are the bending-induced length difference and refractive index difference between the interference arms, while Δε is the bending-induced local tangential strain difference between the interference cores at the bending point. (n+n(dn/dε)) is determined by the material of the fiber core and the wavelength of the transmission light [31], which can be regarded as a constant for the fiber cores of a homogeneous MCF. One can see from Equation (9) that the extension of the interference arm length L can enhance the curvature sensitivity. Thus, the MMI is inherently suitable for bending sensing with long interference arms and controllable optical path difference.
In addition to the advantages mentioned above, note that the bending-induced local tangential strain is dependent on the bending direction and curvature [32], which can be described as
ε i = − d i R c o s θ b − θ i ; ε j = − d j R c o s θ b − θ j
Δ ε = ε i − ε j
where εi and εj are the bending-induced local tangential strain in core i and core j of the MCF. di and dj are the distances between the two cores and the center of the MCF, respectively. For symmetrical fiber cores in the MCF, di and dj can be regarded as the same. R is the radius of applied fiber bending, and θb and θi are, respectively, the angle of the bending direction and the angular position of core i. As shown in Figure 4, an example is given with the transverse geometric distribution of seven-core fiber. Thus, when the bending direction θb is changed under the same bending radius, the strain difference Δε between the interference cores will change. As a result, the optical path difference between the interference arms will change with the bending direction, as well as the wavelength shift of the interference spectrum, i.e., the curvature sensitivity of the MMI has direction dependence, which can be used for vector-bending measurements that can measure the curvature and bending direction.
Sensors 23 03436 g009 550
Figure 4. Transversal distribution of the fiber cores with the definition of the important geometrical parameters in seven-core fiber [32].
In 2006, Libo Yuan et al. demonstrated a curvature sensor based on dual-core fiber MMI [9], where fiber bending gave rise to the change in the optical path difference of the reflected light in the Michelson interferometer. For dual-core fiber, when the bending direction is perpendicular to the plane of the two cores, the cores will not suffer the tangential strain and exhibit no bending response, so, normally, it can only be used for one-dimensional curvature measurement. To solve this problem, by simultaneously measuring two Michelson interferometers based on two dual-core fibers, which are placed with the two planes of fiber cores arranged vertically, a directional flow velocity sensor was demonstrated by Libo Yuan in 2008 [13]. Thanks to the long interference arms and controllable optical path difference, MMIs have been widely developed for bending [1][9][13][26][33][34] and vibration sensing [7][35], with high sensitivity, a large dynamic sensing range, direction distinguishment ability, and low cross-sensitivity.
On the other hand, by utilizing the change in phase difference between the cores of MCF that is caused by dynamic bending, the MMI has also been used for vibration detection [7][35]. As shown in Figure 5, in 2018, Zhiyong Zhao et al. proposed a vibration sensor based on a seven-core fiber Michelson interferometer, where a fan-in coupler was used to couple light from different single-mode fiber pigtails to each core of the MCF, and two cores were selected to construct the in-fiber integrated Michelson interferometer. By monitoring the output power and calculating the fast Fourier transform of the acquired vibration signal, the frequency of variation can be retrieved [7]. Since the Michelson interferometer is not fabricated by splicing or tapering the fibers, it has the outstanding advantages of ultra-compact size and high mechanical strength. In addition, benefiting from the high sensitivity to bending, variation can cause a remarkable phase shift in the MMI, and in 2011, Feng Peng et al. demonstrated an accelerator by measuring the phase shift amplitude of the MMI, which possesses the advantages of small size, light weight, and immunity to electromagnetic interference in comparison with a traditional electrical accelerometer [35]. Furthermore, since both cores can be affected equally by the variation in temperature, the accelerator is intrinsically immune to environmental temperature changes, which enables high-precision acceleration measurement.
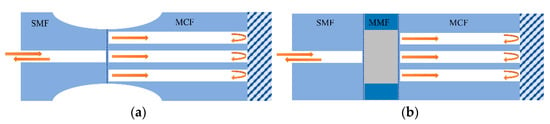
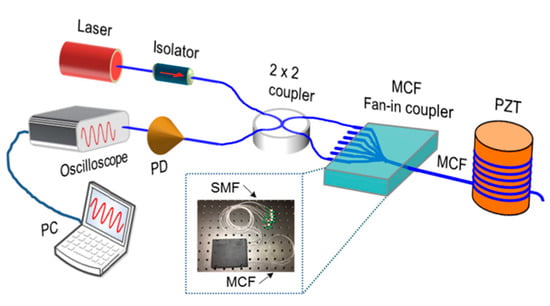
Sensors 23 03436 g011 550
Figure 5. Experimental setup for the MMI vibration sensor [7]. PD: photodetector; PC: personal computer. The inset shows the packaged MCF fan-in coupler.
In addition to the fiber deformation-related measurement mentioned above, the change in the surrounding environment, i.e., refractive index and temperature, can also lead to OPD variation between the side core and the center core of MCF. The light in the side core can interact with the surroundings, while the center core remains less sensitive to the external environment, which leads to the change in OPD and a shift in the transmission spectrum, so the change in surroundings can be retrieved by measuring the wavelength shift [25][27][28]. In 2011, Ai Zhou et al. proposed a refractive index sensor based on an etched asymmetrical dual-core fiber Michelson interferometer [27]. Partial cladding of the MCF was removed by chemical etching to enhance the refractive index sensitivity. The thinning of the fiber cladding leads to leakage of the side core mode and, finally, increases the OPD and enhances the refractive index sensitivity. In addition to the measurement of refractive index, when the ambient temperature is changed, the effective refractive index of the outer core and the center core will change due to the thermal expansion and thermos-optic effect, while the outer cores are more sensitive to the temperature, and the variation in temperature will result in the increase in OPD. Therefore, this feature of the MMI has also been used to develop temperature sensors [16][29][30].

4. MCF-Based Mach–Zehnder Interferometric Sensors

The Mach–Zehnder interferometer (MZI) has been extensively employed in the field of fiber optical sensing since it has the benefits of simple structure, high sensitivity, etc. Thanks to the good spatial consistency and almost the same optical path length between the cores in homogeneous MCFs, the MCF-based Mach–Zehnder interferometer (MMZI) has the advantages of easy fabrication, compact size, good robustness, and long-term stability in comparison with the MZI composed by SMF. As shown in Figure 6, in order to couple light into different cores of an MCF to fabricate the MMZI, the commonly used coupling schemes include tapering at the fusion spliced point or splicing a small segment of MMF between the MCF and SMF. The light is divided into different cores of the MCF at the first fusion region, then travels along different cores individually, and couples back together at the second fusion point and generates interference. Despite resembling the operating principle of the Michelson interferometer, the interference of the MZI is generated by transmitted light instead of reflective light, usually enabling the MZI to have a higher signal-to-noise ratio than the MI. In addition, due to the outstanding advantages of the MMZI, i.e., compact size, simple configuration, easy fabrication, long-term stability, high sensitivity, etc., MMZIs have been widely used for sensing applications of various parameters, which can be classified into bending-related parameters and environmental parameters. In recent years, some novel sensor applications based on the MMZI have been proposed, such as vital signs monitoring [36], microsurgery [37], and distributed vibration sensing [38], showing the prospects of the MMZI in practical application scenarios. Moreover, multicore photonic crystal fibers have also been widely used for MMZIs, and have been developed for measuring temperature [39], strain [40], hydraulic pressure [41], refractive index [42], gas [43], bending [44], etc.
Sensors 23 03436 g013 550
Figure 6. Schematics of the typical coupling methods of the MCF-based Mach–Zehnder interferometer. (a) Tapering the MCF at the fusing point, (b) fusing a segment of MMF between the SMF and MCF.
Similar to the MCF-based Michelson interferometer, the long interference arms and controllable optical path difference enable the MMZI to be widely used for bending-sensing applications [2][14][44][45][46][47][48][49][50][51][52][53][54][55][56][57][58][59][60][61][62]. In 2019, Lei Deng et al. proposed a directional bending sensor with the structure of a three-core-fiber-based MZI, as shown in Figure 7a [46]. By laterally offset-splicing a segment of three-core fiber (TCF) between two SMFs, the light can be split into two cores of the TCF from the input SMF and then pass through the TCF before coupling into the output SMF to generate interference. As shown in Figure 7b, with bending applied, the side core and the inner core will be stretched and extruded, respectively, leading to variation in the optical path difference between the two arms of the MMZI [46]. As a result, the optical path difference will lead to a shift in the interference spectrum, and eventually, the curvature can be retrieved from the wavelength shift. By making use of the same principle in Equation (9), where the strain difference Δε between the interference cores is dependent on the bending radius and direction, the wavelength shift of the interference spectrum will change with the variation in bending direction. Thus, the curvature sensitivity of the MMZI will exhibit direction dependence, which allows for directional bending sensing [46][58][59]. Apart from the bending direction discrimination ability, since the symmetrical cores of MCF have the same sensitivity to their surroundings, e.g., ambient temperature, a curvature sensor with low-temperature cross-sensitivity has been demonstrated [45][55][58], which can compensate for the temperature perturbations and enhance the accuracy of curvature measurement. Moreover, it has been demonstrated that tapering the sensing part of MCF can increase the leakage of the high-order mode of each core to enhance the bending sensitivity. In 2021, Yancheng Ji et al. demonstrated an extremely sensitive curvature sensor with a sensitivity of 174.02957 nm/m−1, which is three or four orders higher than a normal MMZI. The ultrahigh sensitivity of the curvature sensor was achieved due to the structure of the tapered seven-core fiber MMZI, in which the waist diameter of the sensing part was reduced to about 2 µm [55]. In addition, the high sensitivity of bending sensing also enables the MMZI to be used for vibration detection, which has great potential in practical applications, e.g., the long-term monitoring of construction, mechanical structures, and so on [36][63][64]. As shown in Figure 8, in 2020, Fengze Tan et al. proposed contactless vital signs monitoring, based on few-mode fiber and MCF interferometers [36], where the interferometer is placed under the mattress. Human breathing and heartbeat change slightly the pressure that applies to the interferometer, which eventually causes variation in the output waveform. Because of the inherent frequency difference between respiration and heartbeat, the raw data are filtered to recover respiration and heartbeat signals, respectively.
Sensors 23 03436 g014 550
Figure 7. (a) Schematics of a three-core-fiber-based MZI for directional bending sensing. (b) An illustration of the bent three-core MZI [46].
Sensors 23 03436 g015 550
Figure 8. (a) Illustration of the vital signs monitoring experiment. The twin-core fiber (TCF)-based MZI is placed under the mattress. DAQ: data acquisition. (b) Schematic diagram of twin-core fiber MZI vibration sensor; the inset shows the interference spectrum of the measured twin-core-fiber-based MZI [36].
The unique structure of MCF enables the MMZI to measure torsion, as well [11][12][65][66][67]. For example, in 2018, Hailiang Zhang et al. proposed an MMZI-based torsion sensor fabricated by a helical seven-core fiber, in which the side cores are twisted into a spring structure and the center core is almost straight [12]. When external torsion is applied to the fiber, the photo-elastic effect results in a refractive index change in the side cores and cladding, but since the center core is located in the neutral axis of the fiber, theoretically, the torsion-induced refractive index change in the center core is much smaller, and as a result, the change in phase difference between the arms leads to a wavelength shift in the interference spectrum. Due to the photo-elastic effect, the refractive index of the side-core has a positive dependence on the twist rate. Since clockwise and counterclockwise twists give rise to different twist rate variations, i.e., either an increase or decrease in the twist rate, the torsion direction can be determined from the wavelength shift direction of the interference spectrum. As a result, torsion direction discriminative measurement is enabled by using the pre-twisted seven-core fiber MZI sensor. Additionally, since axial strain can also result in variation in the twist rate and the refractive index of the side cores, the helical seven-core-fiber-based MZI can also be used to measure axial transverse strain [68]. Moreover, by making use of the multiple channels in the MCF to generate multiple-path interference, which may have differential responses to external perturbations, e.g., the center core and the side core have different temperature sensitivities, the MCF-based MMZI can achieve multi-parameter measurement. 
Similar to the MCF-based Michelson interferometric sensors, in addition to the curvature/strain-related parameters, such as bending, vibration, axial strain, and torsion, the MMZI is also capable of measuring surrounding environmental parameters, such as refractive index [19][20][69][70][71][72][73][74][75][76][77], ammonia concentration [18], salinity [78], temperature [17][79][80][81][82], magnetic field [83], etc. Because the side cores are usually more sensitive to external disturbances, while the center core remains less sensitive to the external environment, which leads to the change in OPD between the cores and a shift in the transmission spectrum when an environmental parameter changes, the change in external parameters can be retrieved by measuring the wavelength shift of the interference spectrum. On the other hand, etching the cladding or tapering at the sensing region of the MCF can reduce the thickness of the fiber cladding and cause mode leakage of the side cores, which has been used for sensitivity-enhanced refractive index sensing [20][69][70][71][72][73][74][75][76][77] and temperature sensing [17][79][80]. Furthermore, by using special materials to coat the etched or tapered MCF, the sensing sensitivity of targeted parameters can be further improved [17][18][74][83]. For example, the graphene coating can be regarded as a high-index monolayer, which can enhance the evanescent field and increase the interaction between the side cores and the ambient refractive index. In 2020, Donglai Guo et al. proposed a refractive index sensor fabricated by coating the tapered MCF with graphene, as shown in Figure 9, and the result verifies that the evanescent field could be enhanced and the refractive index sensitivity could be improved [74]. In addition to graphene, magnetic fluid is another material that has been widely used to develop MCF sensors. Magnetic fluid is a kind of colloidal solution with magnetic nanoparticles that can aggregate into clusters directly under the applied magnetic field and change the ambient refractive index. In 2018, Chunxia Yue et al. proposed a magnetic sensor fabricated by immersing a segment of tapered MCF into magnetic fluid, as shown in Figure 9b. By measuring the refractive index variation of the magnetic fluid with a tapered MMZI instead of the conventional method of measuring the Faraday rotation of the light, a high-sensitivity MMZI-based magnetic field sensor was achieved [83].
Sensors 23 03436 g017 550
Figure 9. (a) Schematics of the tapered-MMZI-based refractive index sensor, in which the tapered part of the MCF is graphene-coated [74]. PDMS: polydimethylsiloxane substrate. (b) Schematic of the tapered-MMZI-based magnetic-field sensor, in which the sensing part is immersed in epoxy glue filled with the magnetic fluid [83].
In addition to the point sensors, the MCF-based Mach–Zehnder interferometer can also be used for distributed sensing. Due to the spatial length consistency of cores in the MCF, it can be used to implement an MZI that has very long-distance arms. For example, in 2021, Zhiyong Zhao et al. proposed a novel long-range distributed dual MZI vibration sensor, which consisted of two counter-propagating interferometers that were space-division multiplexed in different cores of a weakly coupled seven-core fiber, as shown in Figure 10 [38]. The dual MZI vibration sensor can determine the vibration location through the time-delay difference of two vibration signals in the two MZIs by calculating the cross-correlation of the acquired data, and no additional complicated data processing is required. Since forward-transmitting CW light rather than weak backscattering light is used, together with the advantages of simple structure, a high signal-to-noise ratio, and high sensitivity, the proposed MCF-based dual MZI vibration sensor shows great potential in the application of ultra-long-distance distributed sensing.
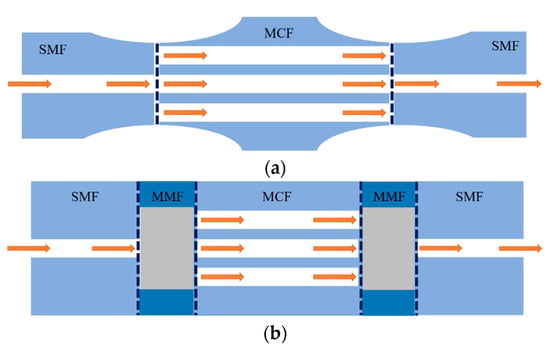
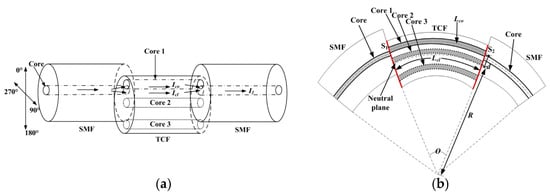
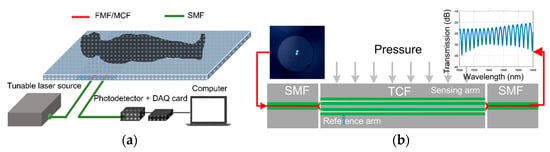
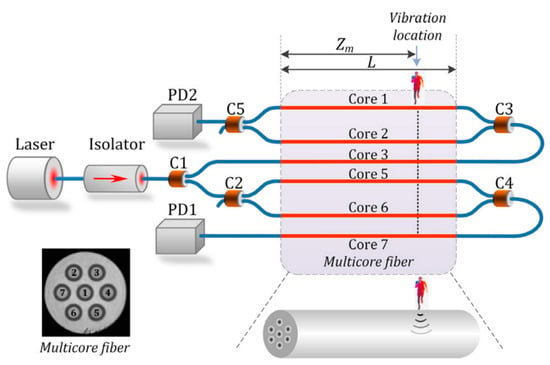
Sensors 23 03436 g018 550
Figure 10. Schematic diagram of the proposed long-range distributed vibration sensor. The inset shows the cross-sectional view of the MCF used. C1–C5: optical couplers [38].

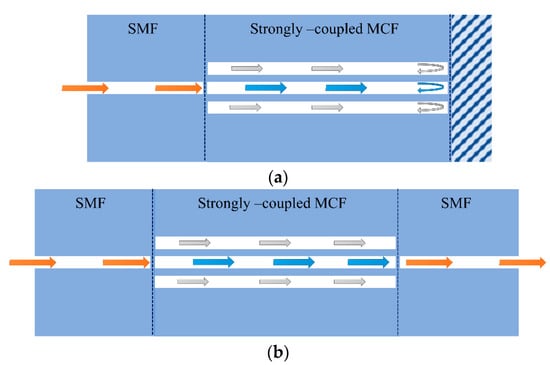
5. Supermode Interferometer-Based (SMI) Sensors

Light transmits independently in different cores of a traditional weakly coupled multicore fiber (MCF), with low crosstalk between cores due to large core-to-core distance. However, in recent years, a new type of strongly coupled multicore fiber with intentionally closely arranged cores has also been proposed, which supports a special mode guiding status, i.e., supermode [84]. The supermode usually has a large effective area because it can be regarded as a superposition of isolated modes of each MCF core. As an example, Figure 11 shows the simulated optical field distribution of supermodes that are excited in three-core fiber and seven-core fiber, respectively [85][86]. The strongly coupled multicore fiber is considered a form of multimode fiber, in which the supermodes can be used to develop modal interferometers for sensing applications. Typical supermode interferometric sensors include transmissive and reflective structures, as shown in Figure 12, i.e., SMF–MCF–SMF (SMS) transmissive structure and SMF–MCF reflective (SMR) structure. The difference in the propagation constants of the supermodes will cause a phase difference in transmission, so the MCF acts in a similar manner to a directional coupler [87][88] and the interference spectrum of the SMI exhibits a periodic maximum and minimum. The changes in fiber length, internal stress, and the effective refractive index of the supermodes will alter the interference spectrum of the interferometer and the coupling power of the supermodes, which can be used to retrieve the sensing parameters. Since different supermodes in the MCF have distinct propagation constants and different sensitivities to external environmental parameters, the external environmental variation can also result in a phase difference between the supermodes, which can be used for the detection of surrounding environmental parameters such as temperature [89][90][91][92][93][94][95][96], refractive index [97], and, simultaneously, temperature and refractive index sensing [98].
Sensors 23 03436 g019 550
Figure 11. Simulated supermodes in the strongly coupled MCF. (a) The orthogonal supermodes in the three-core fiber [85], and (b) the center-core supermode and the symmetrical side-core supermode in the seven-core fiber [86].
Sensors 23 03436 g020 550
Figure 12. Schematics of a supermode interferometer with (a) a reflected structure; (b) a transmitted structure.
Thanks to the large spatial distribution of the fiber mode field of supermodes, bending will easily distort the mode field, which can change the mode loss of each supermode and the phase difference between the supermodes. As a result, bending will result in wavelength shifts [85], light power variation [5], and fringe visibility changes [99] in the SMI, which has been widely used for the high-sensitivity measurement of bending/strain-related external perturbations, such as bending [5][85][86][87][88][99][100][101][102][103][104], vibration [6][8][10][105][106][107][108][109], and strain [110][111]. Furthermore, by using an MCF with asymmetrically distributed cores, the SMI can be used to sense the bending direction.
In addition to the bending and strain sensing applications, supermode interferometers are also capable of sensing the bending-related dynamic parameters, i.e., vibration [6][8][10][105][106][107][108][109]. Due to the large mode spatial distribution of SMIs, bending can easily cause variation in the interference spectrum and the output optical power. Thus, by monitoring the wavelength shift through a high-speed spectrometer [8][10][105][106][107][108][109] or detecting the output optical power variation [6][10], the vibration frequency can be retrieved through the fast Fourier transform (FFT) of the time domain signal.

This entry is adapted from the peer-reviewed paper 10.3390/s23073436

References

  1. Gander, M.; Macrae, D.; Galliot, E.; McBride, R.; Jones, J.; Blanchard, P.; Burnett, J.; Greenaway, A.; Inci, M. Two-axis bend measurement using multicore optical fibre. Opt. Commun. 2000, 182, 115–121.
  2. Zhao, S.; Wang, X.; Yuan, L. Four-core fiber-based bending sensor. Front. Optoelectron. China 2009, 1, 231–236.
  3. Ouyang, Y.; Guo, H.; Ouyang, X.; Zhao, Y.; Zheng, Z.; Zhou, C.; Zhou, A. An In-Fiber Dual Air-Cavity Fabry–Perot Interferometer for Simultaneous Measurement of Strain and Directional Bend. IEEE Sens. J. 2017, 17, 3362–3366.
  4. Ouyang, Y.; Xu, X.; Zhao, Y.; Zhou, A.; Yuan, L. Temperature Compensated Refractometer Based on Parallel Fiber Fabry–Pérot Interferometers. IEEE Photonics Technol. Lett. 2018, 30, 1262–1265.
  5. Amorebieta, J.; Ortega-Gomez, A.; Durana, G.; Fernandez, R.; Antonio-Lopez, E.; Schulzgen, A.; Zubia, J.; Amezcua-Correa, R.; Villatoro, J. Compact omnidirectional multicore fiber-based vector bending sensor. Sci. Rep. 2021, 11, 5989.
  6. Villatoro, J. Phase-shifted modal interferometers for high-accuracy optical fiber sensing. Opt. Lett. 2019, 45, 21–24.
  7. Zhao, Z.; Liu, Z.; Tang, M.; Fu, S.; Wang, L.; Guo, N.; Jin, C.; Tam, H.Y.; Lu, C. Robust in-fiber spatial interferometer using multicore fiber for vibration detection. Opt. Express 2018, 26, 29629–29637.
  8. Villatoro, J.; Antonio-Lopez, E.; Zubia, J.; Schülzgen, A.; Amezcua-Correa, R. Interferometer based on strongly coupled multi-core optical fiber for accurate vibration sensing. Opt. Express 2017, 25, 25734–25740.
  9. Yuan, L.; Yang, J.; Liu, Z.; Sun, J. In-fiber integrated Michelson interferometer. Opt. Lett. 2006, 31, 2692–2694.
  10. Amorebieta, J.; Ortega-Gomez, A.; Durana, G.; Fernandez, R.; Antonio-Lopez, E.; Schulzgen, A.; Zubia, J.; Amezcua-Correa, R.; Villatoro, J. Highly sensitive multicore fiber accelerometer for low frequency vibration sensing. Sci. Rep. 2020, 10, 16180.
  11. Tan, F.; Liu, Z.; Tu, J.; Yu, C.; Lu, C.; Tam, H.-Y. Stable torsion sensor with tunable sensitivity and rotation direction discrimination based on a tapered Trench-Assisted Multi Core Fiber. In Proceedings of the 2018 Optical Fiber Communication Conference (OFC), San Diego, CA, USA, 11–15 March 2018; p. W1K.6.
  12. Zhang, H.; Wu, Z.; Shum, P.P.; Shao, X.; Wang, R.; Dinh, X.Q.; Fu, S.; Tong, W.; Tang, M. Directional torsion and temperature discrimination based on a multicore fiber with a helical structure. Opt. Express 2018, 26, 544–551.
  13. Yuan, L.; Yang, J.; Liu, Z. A Compact Fiber-Optic Flow Velocity Sensor Based on a Twin-Core Fiber Michelson Interferometer. IEEE Sens. J. 2008, 8, 1114–1117.
  14. Tian, Y.; Chai, Q.; Tan, T.; Mu, B.; Liu, Q.; Liu, Y.; Ren, J.; Zhang, J.; Oh, K.; Lewis, E.; et al. Directional Bending Sensor Based on a Dual Side-Hole Fiber Mach–Zehnder Interferometer. IEEE Photonics Technol. Lett. 2018, 30, 375–378.
  15. Wei, G.; Jiang, Q. Needle Shape Sensing with Fabry-Perot Interferometers. IEEE Sens. J. 2021, 21, 22720–22727.
  16. Duan, L.; Zhang, P.; Tang, M.; Wang, R.; Zhao, Z.; Fu, S.; Gan, L.; Zhu, B.; Tong, W.; Liu, D.; et al. Heterogeneous all-solid multicore fiber based multipath Michelson interferometer for high temperature sensing. Opt. Express 2016, 24, 20210–20218.
  17. Cheng, S.; Hu, W.; Ye, H.; Wu, L.; Li, Q.; Zhou, A.; Yang, M.; Zhao, Q.; Guo, D. Tapered multicore fiber interferometer for ultra-sensitive temperature sensing with thermo-optical materials. Opt. Express 2021, 29, 35765–35775.
  18. Fu, H.; Wang, Q.; Ding, J.; Zhu, Y.; Zhang, M.; Yang, C.; Wang, S. Fe2O3 nanotube coating micro-fiber interferometer for ammonia detection. Sens. Actuators B 2020, 303, 127186.
  19. Dong, J.T.; Cheng, C.H.; Wu, C.; Li, J.; Guan, B.O. Highly sensitive optofluidic refractive index sensor based on a seven-liquid-core Teflon-cladding fiber. Opt. Express 2020, 28, 26218–26227.
  20. Guzman-Sepulveda, J.R.; Guzman-Cabrera, R.; Torres-Cisneros, M.; Sanchez-Mondragon, J.J.; May-Arrioja, D.A. A highly sensitive fiber optic sensor based on two-core fiber for refractive index measurement. Sensors 2013, 13, 14200–14213.
  21. Cranch, G.A.; Flockhart, G.M.H.; MacPherson, W.N.; Barton, J.S.; Kirkendall, C.K. Ultra-high-sensitivity two-dimensional bend sensor. Electron. Lett. 2006, 42, 520–522.
  22. Budinski, V.; Donlagic, D. Miniature Twist/Rotation Fabry Perot Sensor Based on a Four-Core Fiber. Proceedings 2018, 2, 1–5.
  23. Liu, G.; Sheng, Q.; Hou, W.; Han, M. Optical fiber vector flow sensor based on a silicon Fabry-Perot interferometer array. Opt. Lett. 2016, 41, 4629–4632.
  24. Zhang, C.; Jiang, Z.; Fu, S.; Tang, M.; Tong, W.; Liu, D. Femtosecond laser enabled selective micro-holes drilling on the multicore-fiber facet for displacement sensor application. Opt. Express 2019, 27, 10777–10786.
  25. Zhou, A.; Li, G.; Zhang, Y.; Wang, Y.; Guan, C.; Yang, J.; Yuan, L. Asymmetrical Twin-Core Fiber Based Michelson Interferometer for Refractive Index Sensing. J. Light. Technol. 2011, 29, 2985–2991.
  26. Zhang, S.; Zhou, A.; Guo, H.; Zhao, Y.; Yuan, L. Highly sensitive vector curvature sensor based on a triple-core fiber interferometer. OSA Contin. 2019, 2, 1953–1963.
  27. Zhou, A.; Zhang, Y.; Li, G.; Yang, J.; Wang, Y.; Tian, F.; Yuan, L. Optical refractometer based on an asymmetrical twin-core fiber Michelson interferometer. Opt. Lett. 2011, 36, 3221–3223.
  28. Shao, M.; Han, L.; Sun, H.; Yin, X.; Qiao, X. A liquid refractive index sensor based on 3-core fiber Michelson interferometer. Opt. Commun. 2019, 453, 1–6.
  29. Mumtaz, F.; Dai, Y.; Wenbin, H.; Abbas, L.G.; Parveen, R.; Ashraf, M.A. A weakly coupled multi-core fibre-based Michelson interferometer composed of an in-fibre coupler. Opto-Electron. Rev. 2021, 29, 117–125.
  30. Shao, M.; Zhang, R.; Gao, H.; Liu, Y.; Qiao, X.; Lin, Y. A High-Sensitivity Low-Temperature Sensor Based on Michelson Interferometer in Seven-Core Fiber. IEEE Photonics Technol. Lett. 2021, 33, 1293–1296.
  31. Bertholds, A.; Dandliker, R. Determination of the Individual Strain-Optic Coefficients in Single-Mode Optical Fibers. J. Light. Technol. 1988, 6, 17–20.
  32. Zhao, Z.; Soto, M.A.; Tang, M.; Thevenaz, L. Distributed shape sensing using Brillouin scattering in multi-core fibers. Opt. Express 2016, 24, 25211–25223.
  33. Qu, H.; Yan, G.F.; Skorobogatiy, M. Interferometric fiber-optic bending/nano-displacement sensor using plastic dual-core fiber. Opt. Lett. 2014, 39, 4835–4838.
  34. Blanchard, P.M.; Burnett, J.G.; Erry, G.; Greenaway, A.H.; Harrison, P.; Mangan, B.; Knight, J.; Russell, P.S.J.; Gander, M.; McBride, R. Two-dimensional bend sensing with a single, multi-core optical fibre. Smart Mater. Struct. 2000, 9, 132–140.
  35. Peng, F.; Yang, J.; Li, X.; Yuan, Y.; Wu, B.; Zhou, A.; Yuan, L. In-fiber integrated accelerometer. Opt. Lett. 2011, 36, 2056–2058.
  36. Tan, F.; Lyu, W.; Chen, S.; Liu, Z.; Yu, C. Contactless vital signs monitoring based on few-mode and multi-core fibers. Opto-Electron. Adv. 2020, 3, 190034.
  37. Zhao, J.; Jia, D.; Nie, A.; Zhang, H.; Liu, T. Compact Vectorial Transverse Force Sensor Based on Two-Modal Interference in a Few-Mode Seven-Core Fiber. J. Light. Technol. 2020, 38, 2046–2052.
  38. Zhao, Z.; Shen, L.; Dang, Y.; Lu, C.; Tang, M. Enabling long range distributed vibration sensing using multicore fiber interferometers. Opt. Lett. 2021, 46, 3685–3688.
  39. Coompson, J.; Colalillo, A.; Twigg, S.; Wynne, R. Multicore photonic crystal fiber thermal sensors. In Proceedings of the IEEE Sensors 2010 Conference, Waikoloa, HI, USA, 1–4 November 2010; pp. 853–855.
  40. Tang, Z.; Lou, S.; Wang, X.; Zhang, W.; Yan, S.; Xing, Z. Using Mode Coupling Mechanism in Symmetrical Triple-Core Photonic Crystal Fiber for High Performance Strain Sensing. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 4500707.
  41. De, M.; Gangopadhyay, T.K.; Singh, V.K. Prospects of Photonic Crystal Fiber as Physical Sensor: An Overview. Sensors 2019, 19, 464.
  42. Pinto, A.M.; Lopez-Amo, M. Photonic crystal fibers for sensing applications. J. Sens. 2012, 2012, 1–21.
  43. Arman, H.; Olyaee, S. Photonic bandgap fiber-based gas sensor with high sensitivity and high birefringence. J. Comput. Electron. 2022, 21, 1357–1364.
  44. MacPherson, W.; Gander, M.; McBride, R.; Jones, J.; Blanchard, P.; Burnett, J.; Greenaway, A.; Mangan, B.; Birks, T.; Knight, J. Remotely addressed optical fibre curvature sensor using multicore photonic crystal fibre. Opt. Commun. 2001, 193, 97–104.
  45. Zhao, Y.; Cai, L.; Li, X.-G. Temperature-Insensitive Optical Fiber Curvature Sensor Based on SMF-MMF-TCSMF-MMF-SMF Structure. IEEE Trans. Instrum. Meas. 2017, 66, 141–147.
  46. Ding, L.; Li, Y.; Zhou, C.; Hu, M.; Xiong, Y.; Zeng, Z. In-Fiber Mach-Zehnder Interferometer Based on Three-Core Fiber for Measurement of Directional Bending. Sensors 2019, 19, 205.
  47. Yuan, L.; Wang, X. Four-beam single fiber optic interferometer and its sensing characteristics. Sens. Actuators A 2007, 138, 9–15.
  48. Li, C.; Ning, T.; Zhang, C.; Li, J.; Zhang, C.; Wen, X.; Lin, H.; Pei, L. All-fiber multipath Mach-Zehnder interferometer based on a four-core fiber for sensing applications. Sens. Actuators A 2016, 248, 148–154.
  49. Wang, X.; Chen, D.; Li, H.; Feng, G.; Yang, J. In-Line Mach–Zehnder Interferometric Sensor Based on a Seven-Core Optical Fiber. IEEE Sens. J. 2017, 17, 100–104.
  50. Wang, Q.; Liu, Y. Optical fiber curvature sensor based on MMF-SCF-MMF structure. Opt. Fiber Technol. 2018, 43, 1–5.
  51. Li, C.; Ning, T.; Li, J.; Zhang, C.; Zhang, C.; Lin, H.; Pei, L. Fiber-Optic Laser Sensor Based on All-Fiber Multipath Mach–Zehnder Interferometer. IEEE Photonics Technol. Lett. 2016, 28, 1908–1911.
  52. Silva, R.; Ferreira, M.; Kobelke, J.; Schuster, K.; Frazão, O. Simultaneous measurement of curvature and strain using a suspended multicore fiber. Opt. Lett. 2011, 36, 3939–3941.
  53. Zhou, R.; Qiao, X.; Wang, R.; Chen, F.; Ma, W. An Optical Fiber Sensor Based on Lateral-Offset Spliced Seven-Core Fiber for Bending and Stretching Strain Measurement. IEEE Sens. J. 2020, 20, 5915–5920.
  54. Chen, W.; Chen, Z.; Qiu, Y.; Kong, L.; Lin, H.; Jia, C.; Chen, H.; Li, H. Highly sensitive optical fiber curvature sensor based on a seven-core fiber with a twisted structure. Appl. Opt. 2019, 58, 8776–8784.
  55. Ji, Y.; Sun, D.; Chen, Y.; Shi, Y.; Cao, J.; Zhang, G.; Han, Z.; Wang, C.; Zhu, X. A High Sensitivity Curvature Sensor Based on Microfiber Mach-Zehnder Interferometer with Tapered Seven-Core Fiber. IEEE Sens. J. 2021, 21, 24090–24097.
  56. Harhira, A.; Santos, J.L.; Lapointe, J.; Culshaw, B.; López-Higuera, J.M.; Kashyap, R.; MacPherson, W.N. High sensitivity inline fiber Mach-Zehnder interferometer bend sensor using a twin core fiber. In Proceedings of the Fourth European Workshop on Optical Fibre Sensors, Porto, Portugal, 8–10 September 2010.
  57. Frazao, O.; Silva, S.F.O.; Viegas, J.; Baptista, J.M.; Santos, J.L.; Kobelke, J.; Schuster, K. All Fiber Mach–Zehnder Interferometer Based on Suspended Twin-Core Fiber. IEEE Photonics Technol. Lett. 2010, 22, 1300–1302.
  58. Wang, L.; Zhang, Y.; Zhang, W.; Kong, L.; Li, Z.; Chen, G.; Yang, J.; Kang, X.; Yan, T. Two-dimensional microbend sensor based on the 2-core fiber with hump-shaped taper fiber structure. Opt. Fiber Technol. 2019, 52, 101948.
  59. Yang, J.; Guan, C.; Zhang, J.; Wang, M.; Yang, M.; Zhu, Z.; Wang, P.; Yang, J.; Yuan, L. Low-temperature crosstalk and surrounding refractive index insensitive vector bending sensor based on hole-assistant dual-core fiber. Appl. Opt. 2019, 58, 6597–6603.
  60. Yin, G.; Zhang, F.; Xu, B.; He, J.; Wang, Y. Intensity-modulated bend sensor by using a twin core fiber: Theoretical and experimental studies. Opt. Express 2020, 28, 14850–14858.
  61. Wang, S.; Zhang, W.; Chen, L.E.I.; Zhang, Y.; Geng, P.; Wang, B.; Yan, T.; Li, Y.; Hu, W. Bending Vector Sensor Based on the Multimode-2-Core-Multimode Fiber Structure. IEEE Photonics Technol. Lett. 2016, 28, 2066–2069.
  62. Guan, C.; Zhong, X.; Mao, G.; Yuan, T.; Yang, J.; Yuan, L. In-Line Mach–Zehnder Interferometric Sensor Based on a Linear Five-Core Fiber. IEEE Photonics Technol. Lett. 2015, 27, 635–638.
  63. Berghmans, F.; Mignani, A.G.; Gökbulut, B.; Inci, M.N. An interferometric vibration sensor based on a four-core optical fiber. In Proceedings of the Optical Sensing and Detection IV, Brussels, Belgium, 3–7 April 2016.
  64. Cai, L.; Pan, J.; Yue, P.; Zhong, N. Theoretical analysis and application of MTM fiber structure based low-frequency vibration sensor. Optik 2019, 195, 163161.
  65. Tan, F.; Liu, Z.; Tu, J.; Yu, C.; Lu, C.; Tam, H.Y. Torsion sensor based on inter-core mode coupling in seven-core fiber. Opt. Express 2018, 26, 19835–19844.
  66. Liu, C.; Jiang, Y.; Du, B.; Wang, T.; Feng, D.; Jiang, B.; Yang, D. Strain-insensitive twist and temperature sensor based on seven-core fiber. Sens. Actuators A 2019, 290, 172–176.
  67. Wang, X.; Qiao, X.; Yu, D.; Gao, H.; Fan, W. Fiber-optic sensor implanted with seven-core helical structure for measurement of tensile strain and extrusion bending. Opt. Eng. 2019, 58, 046111.
  68. Zhang, H.; Wu, Z.; Shum, P.P.; Dinh, X.Q.; Low, C.W.; Xu, Z.; Wang, R.; Shao, X.; Fu, S.; Tong, W.; et al. Highly sensitive strain sensor based on helical structure combined with Mach-Zehnder interferometer in multicore fiber. Sci. Rep. 2017, 7, 1–10.
  69. Jiang, Y.; Wang, T.; Liu, C.; Feng, D.; Jiang, B.; Yang, D.; Zhao, J. Simultaneous measurement of refractive index and temperature with high sensitivity based on a multipath fiber Mach-Zehnder interferometer. Appl. Opt. 2019, 58, 4085–4090.
  70. Zhang, C.; Ning, T.; Li, J.; Zheng, J.; Gao, X.; Lin, H.; Pei, L. Etching twin core fiber for the temperature-independent refractive index sensing. J. Opt. 2018, 20, 045802.
  71. Duan, S.; Liu, B.; Zhang, H.; Zhang, X.; Liu, H.; Wu, J.; Yao, Y. Intensity-interrogated refractive index sensor based on exposed-core multicore fiber Mach-Zehnder interferometer. In Proceedings of the 2019 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 5–10 May 2019; p. SF3L.7.
  72. Al-Mashhadani, Z.A.A.; Navruz, I. Highly sensitive measurement of surrounding refractive index using tapered trench-assisted multicore fiber. Opt. Fiber Technol. 2019, 48, 76–83.
  73. Shao, Z.; Qiao, X.; Rong, Q. Compact gas refractometer based on a tapered four-core fiber. Appl. Opt. 2018, 57, 10198–10206.
  74. Guo, D.; Wu, L.; Yu, H.; Zhou, A.; Li, Q.; Mumtaz, F.; Du, C.; Hu, W. Tapered multicore fiber interferometer for refractive index sensing with graphene enhancement. Appl. Opt. 2020, 59, 3927–3932.
  75. Qi, Y.; Zhang, J.; Feng, Q.; Zhang, X.; Liu, Y.; Han, Y. A Novel High Sensitivity Refractive Index Sensor Based on Multi-Core Micro/Nano Fiber. Photonic Sens. 2019, 9, 197–204.
  76. Zhang, C.; Ning, T.; Li, J.; Pei, L.; Li, C.; Lin, H. Refractive index sensor based on tapered multicore fiber. Opt. Fiber Technol. 2017, 33, 71–76.
  77. Cheng, P.; Yang, M.; Hu, W.; Guo, D.; Du, C.; Luo, X.; Mumtaz, F. Refractive index interferometer based on SMF-MMF-TMCF-SMF structure with low temperature sensitivity. Opt. Fiber Technol. 2020, 57, 102233.
  78. Guzman-Sepulveda, J.R.; Ruiz-Perez, V.I.; Torres-Cisneros, M.; Sanchez-Mondragon, J.J.; May-Arrioja, D.A. Fiber Optic Sensor for High-Sensitivity Salinity Measurement. IEEE Photonics Technol. Lett. 2013, 25, 2323–2326.
  79. Chunxia, Y.; Hui, D.; Wei, D.; Chaowei, X. Weakly-coupled multicore optical fiber taper-based high-temperature sensor. Sens. Actuators A 2018, 280, 139–144.
  80. Mumtaz, F.; Cheng, P.; Li, C.; Cheng, S.; Du, C.; Yang, M.; Dai, Y.; Hu, W. A Design of Taper-Like Etched Multicore Fiber Refractive Index-Insensitive a Temperature Highly Sensitive Mach-Zehnder Interferometer. IEEE Sens. J. 2020, 20, 7074–7081.
  81. Li, H.; Li, H.; Meng, F.; Lou, X.; Zhu, L. All-fiber MZI sensor based on seven-core fiber and fiber ball symmetrical structure. Opt. Lasers Eng. 2019, 112, 1–6.
  82. Zhao, Z.; Tang, M.; Fu, S.; Liu, S.; Wei, H.; Cheng, Y.; Tong, W.; Shum, P.P.; Liu, D. All-solid multi-core fiber-based multipath Mach–Zehnder interferometer for temperature sensing. Appl. Phys. B Lasers Opt. 2013, 112, 491–497.
  83. Yue, C.; Ding, H.; Liu, X. Magnetic-Field Measurement Based on Multicore Fiber Taper and Magnetic Fluid. IEEE Trans. Instrum. Meas. 2019, 68, 688–692.
  84. Xia, C.; Bai, N.; Ozdur, I.; Zhuo, X.; Li, G. Supermodes for optical transmission. Opt. Express 2011, 19, 16653–16664.
  85. Villatoro, J.; Van Newkirk, A.; Antonio-Lopez, E.; Zubia, J.; Schulzgen, A.; Amezcua-Correa, R. Ultrasensitive vector bending sensor based on multicore optical fiber. Opt. Lett. 2016, 41, 832–835.
  86. Kalli, K.; Mendez, A.; Villatoro, J.; Antonio-Lopez, E.; Van Newkirk, A.; Zubia, J.; Schülzgen, A.; Amezcua-Correa, R. Supersensitive sensors based on multicore optical fibres. In Proceedings of the Micro-Structured and Specialty Optical Fibres IV, Prague, Czech Republic, 15–16 April 2015.
  87. Guzman-Sepulveda, J.R.; May-Arrioja, D.A. In-fiber directional coupler for high-sensitivity curvature measurement. Opt. Express 2013, 21, 11853–11861.
  88. Salceda-Delgado, G.; Van Newkirk, A.; Antonio-Lopez, J.E.; Martinez-Rios, A.; Schulzgen, A.; Amezcua Correa, R. Compact fiber-optic curvature sensor based on super-mode interference in a seven-core fiber. Opt. Lett. 2015, 40, 1468–1471.
  89. Van Newkirk, A.; Eznaveh, Z.S.; Antonio-Lopez, E.; Salceda-Delgado, G.; Schülzgen, A.; Amezcua-Correa, R. High temperature sensor based on supermode interference in multicore fiber. In Proceedings of the 2014 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 8–13 June 2014; p. SM2N.7.
  90. Antonio-Lopez, J.E.; Eznaveh, Z.S.; LiKamWa, P.; Schulzgen, A.; Amezcua-Correa, R. Multicore fiber sensor for high-temperature applications up to 1000 degrees C. Opt. Lett. 2014, 39, 4309–4312.
  91. Wales, M.D.; Clark, P.; Thompson, K.; Wilson, Z.; Wilson, J.; Adams, C. Multicore fiber temperature sensor with fast response times. OSA Contin. 2018, 1, 764–771.
  92. Amorebieta, J.; Ortega-Gomez, A.; Fernández, R.; Antonio-Lopez, E.; Schülzgen, A.; Zubia, J.; Amezcua-Correa, R.; Durana, G.; Villatoro, J. Sensitivity-optimized strongly coupled multicore fiber-based thermometer. Opt. Laser Technol. 2022, 145, 107532.
  93. Amorebieta, J.; Durana, G.; Ortega-Gomez, A.; Fernandez, R.; Velasco, J.; Saez de Ocariz, I.; Zubia, J.; Antonio-Lopez, J.E.; Schulzgen, A.; Amezcua-Correa, R.; et al. Packaged Multi-Core Fiber Interferometer for High-Temperature Sensing. J. Light. Technol. 2019, 37, 2328–2334.
  94. Antonio-Lopez, E.; Salceda-Delgado, G.; Van Newkirk, A.; Schülzgen, A.; Amezcua-Correa, R. Multiplexed high temperature sensor based on multicore fiber. In Proceedings of the Advanced Photonics, Barcelona, Spain, 27–31 July 2014 ; p. SeW4C.
  95. Cuando-Espitia, N.; Fuentes-Fuentes, M.A.; Velazquez-Benitez, A.; Amezcua, R.; Hernandez-Cordero, J.; May-Arrioja, D.A. Vernier effect using in-line highly coupled multicore fibers. Sci. Rep. 2021, 11, 18383.
  96. Van Newkirk, A.; Antonio-Lopez, E.; Salceda-Delgado, G.; Amezcua-Correa, R.; Schulzgen, A. Optimization of multicore fiber for high-temperature sensing. Opt. Lett. 2014, 39, 4812–4815.
  97. May-Arrioja, D.A.; Guzman-Sepulveda, J.R. Highly Sensitive Fiber Optic Refractive Index Sensor Using Multicore Coupled Structures. J. Light. Technol. 2017, 35, 2695–2701.
  98. Flores-Bravo, J.A.; Fernandez, R.; Antonio Lopez, E.; Zubia, J.; Schulzgen, A.; Amezcua Correa, R.; Villatoro, J. Simultaneous Sensing of Refractive Index and Temperature with Supermode Interference. J. Light. Technol. 2021, 39, 7351–7357.
  99. Vallés, J.A.; Benedicto, D. Optimized active multicore fiber bending sensor. Opt. Mater. 2019, 87, 53–57.
  100. Capilla-Gonzalez, G.; May-Arrioja, D.A.; Lopez-Cortes, D.; Guzman-Sepulveda, J.R. Stress homogenization effect in multicore fiber optic bending sensors. Appl. Opt. 2017, 56, 2273–2279.
  101. Newkirk, A.V.; Antonio-Lopez, J.E.; Velazquez-Benitez, A.; Albert, J.; Amezcua-Correa, R.; Schulzgen, A. Bending sensor combining multicore fiber with a mode-selective photonic lantern. Opt. Lett. 2015, 40, 5188–5191.
  102. Salceda-Delgado, G.; Van-Newkirk, A.; Lopez, J.A.; Schülzgen, A.; Correa, R.A. Optical fiber curvature sensors based on single mode-7 core-single mode fiber structures. In Proceedings of the Advanced Photonics, Barcelona, Spain, 27–31 July 2014; p. SeW3C.2.
  103. Villatoro, J.; Amorebieta, J.; Ortega-Gomez, A.; Antonio-Lopez, E.; Zubia, J.; Schülzgen, A.; Amezcua-Correa, R. Composed multicore fiber structure for direction-sensitive curvature monitoring. APL Photonics 2020, 5, 070801.
  104. Arrizabalaga, O.; Sun, Q.; Beresna, M.; Lee, T.; Zubia, J.; Velasco Pascual, J.; Saez de Ocariz, I.; Schulzgen, A.; Antonio-Lopez, J.E.; Amezcua-Correa, R.; et al. High-performance vector bending and orientation distinguishing curvature sensor based on asymmetric coupled multi-core fibre. Sci. Rep. 2020, 10, 14058.
  105. Villatoro, J.; Antonio-Lopez, E.; Schulzgen, A.; Amezcua-Correa, R. Miniature multicore optical fiber vibration sensor. Opt. Lett. 2017, 42, 2022–2025.
  106. Villatoro, J.; Flores-Bravo, J.; Arrospide, E.; Arrizabalaga, O.; Antonio-Lopez, E.; Zubia, J.; Schülzgen, A.; Amezcua-Correa, R. Packaged Multi-core Fiber Interferometric Vibration Sensor. In Proceedings of the 2018 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 13–18 May 2018; p. SM2K.6.
  107. Villatoro, J.; Arrizabalaga, O.; Antonio-Lopez, E.; Zubia, J.; de Ocáriz, I.S. Multicore fiber sensors. In Proceedings of the 2017 Optical Fiber Communication Conference (OFC), Los Angeles, CA, USA, 19–23 March 2017; p. Th3H.1.
  108. Villatoro, J.; Ortega-Gomez, A.; Zubia, J.; Antonio-Lopez, E.; Schülzgen, A.; Amezcua-Correa, R. Ultrasensitive vibration sensor based on an asymmetric multi-core optical fiber. In Proceedings of the 26th International Conference on Optical Fiber Sensors, Lausanne, Switzerland, 24–28 September 2018.
  109. Villatoro, J.; Arrizabalaga, O.; Diez, M.; Arrospide, E.; Antonio-Lopez, E.; Zubia, J.; Schülzgen, A.; Amezcua-Correa, R. Simple Multi-core Optical Fiber Accelerometer. In Proceedings of the Advanced Photonics Congress Optical Sensors 2018, ETH, Zürich, Switzerland, 2–5 July 2018.
  110. Villatoro, J.; Arrizabalaga, O.; Durana, G.; Saez de Ocariz, I.; Antonio-Lopez, E.; Zubia, J.; Schulzgen, A.; Amezcua-Correa, R. Accurate strain sensing based on super-mode interference in strongly coupled multi-core optical fibres. Sci. Rep. 2017, 7, 4451.
  111. Van Newkirk, A.; Antonio-Lopez, J.E.; Salceda-Delgado, G.; Piracha, M.U.; Amezcua-Correa, R.; Schulzgen, A. Multicore Fiber Sensors for Simultaneous Measurement of Force and Temperature. IEEE Photonics Technol. Lett. 2015, 27, 1523–1526.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
This entry is offline, you can click here to edit this entry!
ScholarVision Creations
Feedback