Your browser does not fully support modern features. Please upgrade for a smoother experience.
Please note this is an old version of this entry, which may differ significantly from the current revision.
Subjects:
Remote Sensing
The leaf inclination angle (LIA), defined as the leaf or needle inclination angle to the horizontal plane, is vital in radiative transfer, precipitation interception, evapotranspiration, photosynthesis, and hydrological processes. The remote sensing methods to estimate LIA are mainly based on the empirical, radiative transfer model, and gap fraction methods. More advanced inversion strategies and validation studies are necessary to improve the robustness of LIA remote sensing estimation.
- leaf inclination angle
- remote sensing estimation
1. Introduction
Leaf inclination angle (LIA) quantifies the inclination of the leaf or needle to the horizontal plane or the angle between the leaf surface normal and zenith (Figure 1a) [1]. LIA is formed under the comprehensive regulation of genes, hormones, and environmental factors, including light, water, temperature, and nutrition [2,3,4]. LIA is a key plant structural trait that determines radiative transfer [5,6], rainfall interception [7], and evapotranspiration [8], and thus affects photosynthesis and hydrological processes [4,5,9].
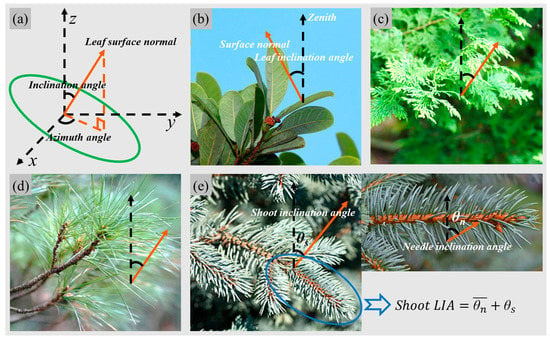
Figure 1. The schematic of leaf orientation (a) and the leaf inclination angle (LIA) measurement for broad leaf (b) and needle leaves of cypress (c), pine (d), and spruce (e). In (e), the LIA of a specified shoot is the sum of the average inclination angle for all needles within a horizontally placed representative shoot ( ) and the shoot inclination angle (θs).
The probability density of LIA or the fraction of leaf area per unit LIA is expressed with the leaf angle distribution (LAD) function [10]. Theoretically, LAD can be categorized into the planophile, erectophile, extremophile, plagiophile, uniform, and spherical distributions [10]. The spherical distribution assumes that the relative probability density of the LIA is the same as the area of the corresponding sphere surface element [10]. LAD can also be described by statistical distribution functions such as the ellipsoidal distribution [11], rotated-ellipsoidal distribution [12], and two-parameter beta distribution [13]. In radiative transfer, the leaf projection function (G(θ)) is calculated as the average projection ratio of unit leaf area in the illumination or viewing direction θ [6,14]. The spherical distribution is characterized by an isotropic leaf projection function (G ≡ 0.5) [10].
Remote sensing methods provide large-scale and continuous LIA mapping based on empirical relationships, radiative transfer model inversion, and the gap fraction method [17,18,19,74].
2. Empirical Methods
MLA can be estimated empirically from canopy reflectance or vegetation indices by constructing a transfer function [75]. Zou and Mõttus [75] found that the near-infrared (NIR) reflectance, especially in the 748 nm in the red-edge band, showed a negative linear relationship with the crop MLA and the output MLA showed medium consistency with the reference MLA. They also showed that the MLA can be determined from the red and blue reflectance space, but the estimated MLA showed poor correspondence with the reference value [75]. Different LAD types can also be empirically distinguished. For example, Huang, Niu, Wang, Liu, Zhao, and Liu [17] identified different winter wheat LAD types from the multi-temporal NIR reflectance. In simulation studies, the backscattering coefficient of the microwave horizontal polarization was found to correlate to LAD [76], but no LIA inversion studies with microwaves have been reported.
The angular reflectance varies with MLAs and can assist the MLA estimation [77]. The angular reflectance is commonly described by the bidirectional reflectance distribution function (BRDF). One of the widely used BRDF models is the semi-empirical Ross-Li model, which characterizes the bidirectional reflectance with a linear combination of the volumetric, geometric, and isotropic kernels [78]. The structural parameter-sensitive index (SPEI) has been constructed from BRDF weights to identify the winter wheat LAD types [17].
where and are the weights of the isotropic and volumetric scattering kernels in the NIR band, respectively, and is the weight of the geometric scattering kernel in the red band [17,79].
The vegetation index (VI) has shown great potential to estimate MLA because of its simplicity and capability to mitigate the soil background effect [80,81]. Existing simulation studies have shown that the modified triangular vegetation index (MTVI2) [82] and two-band enhanced vegetation index (EVI2) [83] are strongly correlated negatively with MLA, especially for low and medium LAI (LAI < 3) [80].
The empirical method is easy to use, but it relies on a large number of field measurements, which limits the method’s generality. Currently, the method has been applied to crops with medium accuracy [75]. The applicability of this method to noncrops needs to be further explored. The reflectance-based method is easily affected by LAI, leaf dry matter content, and soil background [77,81,84]. The method works better for the medium LAI conditions when the impacts of those factors are suppressed [77,81,84]. The angular reflectance has been used to distinguish different LAD types qualitatively [17] and is promising for estimating LIA quantitatively. The VI method suppresses the soil background and chlorophyll impact and more effort can be made to estimate LIA from VI in practice. Combining multiple vegetation indices may also help decouple LIA from the LAI and leaf dry matter impact.
3. Radiative Transfer Model Methods
Radiative transfer models link canopy reflectance with a series of leaf optical properties and canopy structural parameters (LAD, LAI, and CI) for different solar-viewing geometries [6,85,86]. The RTM method obtains an optimal solution that minimizes the cost function between the simulated and observed reflectance using the look-up table, numerical optimization, and machine learning technologies [87]. Currently, most LAD retrievals are based on the PROSAIL model which integrates the PROSPECT leaf spectral model [88] and the Scattering by Arbitrarily Inclined Leaves (SAIL) canopy bidirectional reflectance model [85].
Multi-angle reflectance is commonly used for LAD retrieval [18,77,89]. For example, Jacquemoud et al. [89] retrieved LAD from the ground and airborne multi-angle NIR reflectance based on the PROSAIL model but the result was not satisfactory, especially for canopies with high LAI and horizontal LAD. Ferreira et al. [90] inverted the individual crown LIA from the airborne imaging spectroscopy based on the discrete anisotropic radiative transfer (DART) model and look-up table method. The RTM method has also been applied to estimate the seasonal grassland MLA from the Landsat reflectance, but the result showed strong anomalous fluctuations [91]. Currently, the RTM method is only validated with field measurements in a direct point-to-pixel manner for crops [75,91].
The RTM method has mainly been applied in local regions, but the method is promising for large-scale LIA time series mapping. However, the method is affected by the different LAD settings in radiative transfer models (Bacour et al. [92]). The method is also affected by the ill-posed problem in the inversion process [18,90,91]. Several approaches have been proposed to improve LIA retrieval through regularization with prior information. One solution is to provide background characteristics in the RTM inversion, such as the VI-LAI empirical relationship, leaf spectral, soil reflectance, and skylight fraction [18,84]. The temporal constraint assumes that the seasonal variation of the LIA is negligible [84]. The object-based inversion strategy exerts spatial constraint on the inversion process by assuming that the LIAs of adjacent pixels are similar [19].
4. The Gap Fraction Method
The gap fraction method can also be used to estimate the global leaf projection function (G) from remote sensing data [74]. For example, the global nadir leaf projection function G(0) can be estimated based on the Beer–Lambert law (Equation (1)):
where the nadir gap fraction is calculated from the fractional vegetation cover (P(0) = 1 − FVC) and the nadir clumping index (CI(0)) is approximated by the whole CI [74]. However, this method to estimate G is limited by the accuracy and consistency of remote sensing products [93].
This entry is adapted from the peer-reviewed paper 10.3390/rs15040946
This entry is offline, you can click here to edit this entry!
