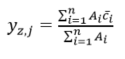Multi-motor systems are strong coupled multiple-input–multiple-output systems with independent or mechanically interconnected motors. The main objective in multi-motor drive control is to achieve synchronized operation of all motors in the system. In this paper, multi-motor systems are classified in accordance with their control demands. The review of recent research literature indicates that fuzzy algorithms are widely used in multi-motor control.
- multi-motor systems
- fuzzy logic control
- speed control
- coordinated control
1. Introduction
Multi-motor drives are an optimal solution for high-inertia and high-power drives, such as belt conveyors [1], as well as for long continuous lines [2]. In recent years, multi-motor drives have been increasingly implemented in electric vehicles [3] and robot manipulators [4]. Depending on drive application, control objectives are defined. Clearly, the control objectives can considerably differ depending on drive application. For example, the main objective of drive control used in continuous lines is the decoupled tracking of speed and tension. On the other hand, in electrical vehicles, the main goal of drive control is speed control with torque distribution to ensure the stability of such a vehicle. The energy efficiency improvement of the multi-motor system is also an important demand in industry and transport applications. The multi-motor system’s energy efficiency improvement possibilities are presented in [1][5].
The development of a multi-motor system control begins with choosing the relationships between motor drive units and determining the number and type of feedbacks and controllers, i.e., establishing the multi-motor control strategy. The next step is development and implementation of control algorithms which will ensure the stability and desired behavior of the system. The variety of control algorithms is developed for multi-motor system control, such as classic proportional-integral-derivative (PID) control, optimal control, control methods based on artificial intelligence, etc. In the development of new multi-motor control strategies, fuzzy logic control is widely used. It has been reported that the implementation of fuzzy logic control gives encouraging results in real-time speed error compensation [4], drive efficiency increase [1], and in rather simple and fast synchronizing rules.
The main goal of this paper is to provide a survey of multi-motor system control with emphasis on fuzzy logic control, whilst taking into consideration different control objectives of different multi-motor systems. Section 2 examines the categorization of multi-motor systems considering their demands and specific characteristics. In Section 3, an overview of fuzzy logic algorithms used in multi-motor control is given with the analysis of different functionalities that fuzzy controllers handle in multi-motor synchronization strategies. Finally, Section 4 presents the conclusion of presented research analysis.
2. Multi-Motor Systems Classification
In Reference [6], multi-motor systems are divided into two major categories: systems with independent motors and systems with mechanically interconnected motors. In the literature, the term multi-motor system usually corresponds to systems with interconnected motors. Typically, each mechanical section of such a system is driven by a fully controlled drive unit, and all these drives are electronically synchronized through the master reference command [7]. A drive unit usually consists of a frequency converter and a motor, whereas the master reference command is generated in the master programmable logic controller (PLC).
Multi-motor systems are complex, often with nonlinear behavior that cannot be neglected. In addition, coordinated performance of all multi-motor system parts is affected by various external factors [8]. This yields a need for the development of fast and reliable multi-motor synchronization techniques. The proper synchronization technique depends on multi-motor system objectives and demands. Based on the objectives stated in the reviewed literature, the multi-motor systems with interconnected motors can be divided into three categories: continuous lines, robotic manipulators and electrical vehicles. The overview of objectives for these categories is presented in Table 1. These categories will be described in this section in detail.
Table 1. Multi-motor system control objectives.
|
Multi-Motor System Type |
Equal Speed for All Motors |
Equal Torque/Tension for All Motors |
Torque Distribution |
High Precision of Positioning |
Adjustable Acceleration/ Deceleration Rates |
Preset Motion Path |
|
Continuous lines |
+ |
+ |
− |
− |
+ |
+ |
|
Robotic manipulators |
− |
− |
+ |
+ |
+ |
+ |
|
Electrical vehicles |
− |
− |
+ |
+ |
+ |
− |
Some multi-motor systems have very specific demands and cannot be placed in the mentioned categories. Examples of such systems are the cutterhead driving system of shield machines [9] and vibration systems [10]. For the cutterhead driving system of shield machines, it is very important to achieve an equal speed and equal torque of all motors, otherwise some motors may be overloaded. Vibration systems have multiple vibration exciters for which speed and phase synchronization must be ensured.
Some complex systems incorporate multi-motor subsystems of different categories. An example of such a system is gantry cranes. The first subsystem is the hoist for raising and lowering the cargo. The second is the trolley for positioning the hoist, and the third is a gantry for driving the gantry crane through the working area. The most important feature for maintaining the stability of gantry cranes is load torque distribution. The load torque distribution techniques applicable on gantry crane systems are categorized and described in Reference [11].
2.1. Multi-Motor Systems in Continuous Lines
Continuous lines can be modeled as nonlinear multiple-input–multiple-output (MIMO) systems with a strong mutual effect between the individual input and state quantities [2]. The mechanical interconnections between motor shafts are characterized by effects of elasticity, friction and backslash. The two-motor drive system model considering these effects is given in References [12] [8]. The control goals for continuous lines are summarized in Reference [13] as follows: decoupled control of tension and speed values, invariance against additive disturbances, robustness against changes of important line parameters, dynamic responses of controlled variables without any overshoots, and stability of the controlled system. According to Reference [14], the main objective in the regulation of such systems is to ensure that the belt or processed material’s velocity is as high as possible, while controlling its tension over the entire production line. Examples of continuous line systems are web winding systems and conveyor belts. If the control of a web winding system is not properly synchronized, then damaging, breaking and folding of material will occur [14]. In the case of conveyor belts, the lack of system synchronization may lead to spillage of the material over the belt or nonsymmetrical distribution of the material across the profile of the belt [1].
Another example of continuous lines is filling systems in the food packaging industry. According to Reference [15], the specific problems occur in the case of filling thick sauces and sticky food because of sudden load changes at the filling motor. These abrupt load changes lead to large synchronization errors in the multi-motor system.
2.2. Multi-Motor Systems in Robotic Manipulators
Robotic manipulators are another type of multi-motor systems [4]. In this type of multi-motor systems, the main goals are to ensure the precision of tool positioning, the precise amount of force acting on a processed object, and coordinated movement according to the reference path defined by inverse kinematics in the dynamical state. As stated in Reference [4], at present, robot manipulators are still built with weak anti-interference ability, i.e., it is still hard for robots to interact dynamically with their environment, which, in most cases, must be controlled [16]. To improve robot manipulator performance, the authors of [4] point out the importance of studying multi-motor coordinated technology. In this multi-motor system category, all other machines with synchronized multi-axis positioning tasks, such as machines for complex parts manufacturing, can be incorporated.
2.3. Multi-Motor Systems in Electrical Vehicles
In recent years, electrical vehicles have been developed with multi-motor drives. In this type of multi-motor drive, the most important objective is to maintain stability of the vehicle. To achieve stability of the vehicle, the driving torque and motor speeds must be properly distributed in every operation point (e.g., acceleration, deceleration, and vehicle turning left/right). According to Reference [3], the two-side motor-independent drive is the most widely used transmission scheme, and the synchronization and coordination control problem is a key problem in the research and development of this kind of vehicle. The authors of Reference [17] point out another feature necessary for the reliability of electrical vehicles: the electrical vehicle must be a fault-tolerant system, i.e., in the case of one drive unit failure, the stability of the system must be maintained with the rest of the drive units. This being the case, the authors propose a fault-tolerant controller based on sliding mode techniques. Further bibliographic review and study of fault-tolerant diagnosis and control systems for multi-motor electric vehicles can be found in Reference [18]. The implementation of the electrical vehicle drive control algorithm with torque distribution on an FPGA platform is described in Reference [19]. In Reference [20], a new type of braking power distribution for distribution-driven electrical vehicles is introduced. The road state and condition estimation as well as the relationship between the tire and road surface are described and considered in slip controller design.
3. Fuzzy Algorithms in Multi-Motor System Control
As discussed in Section 2, multi-motor systems are strongly coupled nonlinear MIMO systems. These systems are complex and hard to model considering all nonlinearities and mechanical coupling effects. In addition, many uncertainties caused by external conditions (wind gusts and unpredictable road conditions for electrical vehicles, material thickness and spacing on the conveyor belts for continuous lines, etc.) can affect the operating conditions of individual motors in the system. This being the case, fuzzy algorithms are convenient for implementation in multi-motor system control because of the following two advantages: the fuzzy algorithm is based on defining states similar to narrative expression of experience, and the needed knowledge of controlled technology is minimal. This means that nonlinear input/output relationships can be expressed by a set of qualitative “if–then” rules [2]. Further on, as pointed out in Reference [4], fuzzy control can be used to distinguish different types of disturbances to different fuzzy areas during operation and, thus, improve the coordination of the multi-motor operation. Two different fuzzy inference systems exist, namely, the Mamdani and the Takagi–Sugeno inference systems. The Takagi–Sugeno fuzzy rule base uses linear functions of inputs to predict the output, whereas the Mamdani inference system determines outputs through fuzzy sub-sets [21]. A detailed review of Mamdani inference systems is given in Reference [22], and in Reference [23] Takagi–Sugeno fuzzy modeling is described.
In research papers dealing with multi-motor control, there are several different functionalities of fuzzy logic control reported. The fuzzy algorithms are used for modelling nonlinear coupling effects between individual drives in the system; for speed control of individual motors; and as compensators used in the ring coupling control strategy, the relative coupling strategy, the adjacent tracking strategy or coordinators if the coordinated control strategy is used. The fuzzy-based model of nonlinear coupling effects between individual drives in the continuous line system is developed in Reference [2].
The theoretical background of fuzzy PID controllers can be found in Reference [24]. Fuzzy controllers used as compensators or for speed regulation usually have two inputs, error e and error change ec=de/dt and one [4][8] or two outputs [25][26]. The authors mostly use three [12][26], five [25][27][28] or seven [4][29] membership functions for inputs. The number of membership functions defined for output variables in most cases is the same as the number of membership functions for input variables, but may be smaller [1] or larger [8][30] depending on application. For example, in Reference [8], there are seven membership functions for each input and thirteen membership functions for the output variable. For fuzzy logic controllers used in multi-motor system control, to calculate the output scale value, the most often used methods are the center of gravity and the weighted average. As stated in Reference [21], the center of gravity method is used with the Mamdani model and weighted average in the Takagi–Sugeno model. The center of gravity defuzzification method for continuous functions is given with the following equation [4]:
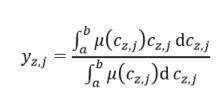 |
(1) |
where denotes the output fuzzy set corresponding to the z-th error fuzzy set , the j-th fuzzy set of error change , denotes the membership function of the output, and is the control output value. For discrete functions, the center of gravity method is given with Equation (3) [31]:
|
|
(2) |
where represents the sub-area of the total area A of output membership function distribution, represents the centroid of the sub-area, and n represents the number of the sub-area of A. The weighted average is defined as [29]:
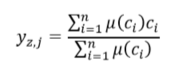 |
(3) |
In Equation (4), denotes the membership function, represents the middle element of the i-th fuzzy set, and n represents the number of output membership functions. It is important to note that the weighted average method can be used only with symmetrical membership functions.
When designing a fuzzy controller, authors often encounter the problem of a large overshoot in the case of larger input value changes. This problem can be solved by introducing a larger number of membership functions for a more detailed description of the desired behavior of the controller. An example of this phenomenon is motor start-up. In this case, the control error is big and positive, and the control error change is also big and positive, thus, the control output should be big and positive. As the motor speed increases, the control error decreases. If the output remains the same, a large speed overshoot will occur. This means that the control output should now be small and positive, or even negative, depending on the control error change rate. However, it should be noted that the larger number of membership functions describing behavior of input and output variables implies a larger number of fuzzy rules (typically, if the number of membership functions for each variable is n, the number of rules equals n2) and a slower control algorithm. Another problem is the time-consuming tuning of the fuzzy controller. These two problems can be solved using artificial intelligence algorithms, such as neural networks [2], immune control [30], particle swarm optimization or simulated annealing [26] for tuning the fuzzy controller.
3.1. Fuzzy Speed Controllers for Individual Motors of Multi-Motor System
The fuzzy PID algorithm for control of the slave motor speed in the two-motor system is reported in Reference [32]. The chosen synchronization strategy for the two-motor system is master–slave. A similar adaptive fuzzy PID controller is developed in Reference [8] for the three-motor system. According to the authors, such a controller enables fast tracking and disturbance elimination. In Reference [33], a genetic algorithm is used to adjust the rules and membership functions of speed fuzzy PID controllers implemented in the digital signal processor (DSP) for control of a multi-fingered robot manipulator.
In Reference [29], the authors propose variable universe fuzzy PI speed controllers for permanent magnet synchronous motors of a multi-motor system. The main goal of introducing the variable universe interpolation is to enable a change in fuzzy rules without increasing the rule number. In this way, if the controlled object (a motor with an operating mechanism) changes, the control quality of the existing controller can be easily improved.
In References [25][34][35], fuzzy logic rules are used to adjust the coefficients of the extended state observer (ESO) to improve the speed control of each drive. The ESO is introduced in control schemes to observe multi-motor system states and lumped disturbances, including nonlinearities and uncertainties. In this way, fuzzy active disturbance rejection control is achieved, which enables disturbance estimation and compensation of a multi-motor system.
Nonlinear fuzzy immune control is implemented in Reference [30]. The presented experimental results show that the multi-motor control strategy with such speed controllers enables decoupling of speed and tension tracking.
3.2. Fuzzy Speed Controllers
In Reference [8], the authors developed a fuzzy coordinator of a multi-motor system. The coordinated controller is tuned to quickly compensate the speed error of a motor with the largest relative error while preserving the stability of the whole system.
In Reference [12], the authors introduced a fuzzy technique proposed by Takagi–Sugeno–Kang to eliminate the chattering phenomenon which occurs in the two-motor drive system with an adaptive sliding mode controller used to obtain tracking effectiveness. The fuzzy algorithm is used to adjust the coefficient of the sliding mode controller.
The authors in Reference [28] introduce robust fuzzy PID controllers of the three-motor system using Simulated Annealing Optimization (SAO). The SAO algorithm is introduced to reduce strong coupling influences between drive units. The proposed method is tested in MATLAB/Simulink simulation of a three-motor system of a belt–pulley. The theoretical background of fuzzy algorithm systems with reduced parametric sensitivity based on simulated annealing optimization can be found in Reference [26].
3.3. Fuzzy Compensators Used in Multi-Motor Systems
In Reference [1], the authors reported practical implementation of fuzzy logic control based on Mamdani’s reasoning methods to achieve the variable acceleration and deceleration of an excavator–conveyor–spreader system on an open-pit mine. Fuzzy logic control was introduced to calculate the acceleration and deceleration rate for a single belt conveyor motor of a drive based on the speed of the previous belt conveyor motor, cross-section of incoming material and the drive torque. The master PLC generates the reference speed which is the input for a classical PI controller that generates the torque reference for the direct torque control. The fuzzy algorithm used in Reference [1] is explained in detail in Reference [27]. In the paper, the relative coupling synchronization strategy is used. The energy efficiency improvement with the newly proposed fuzzy logic controller is experimentally proved. In Reference [36], a combination of particle swarm optimization and fuzzy control was applied in coordinated control of an automated guided vehicle. It is concluded that the proposed control ensures stable operation of such a vehicle with a faster response to disturbances.
The authors in Reference [4] introduced fuzzy compensators in the cross-coupled ring strategy. The fuzzy algorithm is implemented to change the control parameters of the motor speed controllers in real time based on the speed errors of two adjacent motors. The proposed control quality is tested in semi-physical simulation of a four-motor system with the MATLAB/Simulink and the RT-LAB real-time simulation platform. The results show that fuzzy control improves the tracking performance of a multi-motor system.
4. Conclusion
In recent years, the multi-motor systems have been increasingly developed and implemented for industry applications and electrical vehicles. The first step to ensure fast and precise operation of a system prone to disturbances as well as the stability of such a system is to state all of its control demands and objectives. Then, an appropriate synchronization strategy and control methods can be chosen. Due to its nonlinear behavior and the complexity of the system, the control rules are difficult to obtain analytically. Besides, to achieve fast dynamics in reference tracking and disturbance compensation, additional control delay should be avoided. This leads to the conclusion that the control algorithms used in multi-motor system control should be as simple as possible. The control method that fulfills all stated demands is fuzzy logic control. The literature overview presented in this paper shows that the fuzzy logic control algorithms for multi-motor control and synchronization are being increasingly developed. Moreover, successful implementation of fuzzy logic algorithms as speed controllers, compensators and coordinators for multi-motor systems is reported.
This entry is adapted from the peer-reviewed paper 10.3390/electronics9111788
References
- Ristić, L.; Bebić, M.; Jetvić, D.; Jeftenić, B.; Štatkić, S.; Nikolić, A. Controlled multi motor drives of high power belt conveyors: Practical experiences during the exploitation of the system on open pit mine. In Proceedings of the 13th WSEAS International Conference on Electric Power Systems, High Voltages, Electric Machines (POWER 13), Chania, Greece, 27–29 August 2013; pp. 65–70.
- Daniela Perduková; Pavol Fedor; Jan Bacik; Jozef Herčko; Jan Rofar; Multi-motor drive optimal control using a fuzzy model based approach. Journal of Ambient Intelligence and Smart Environments 2017, 9, 329-344, 10.3233/ais-170433.
- Hao Huang; Qunzhang Tu; Chenming Jiang; Limin Ma; Pei Li; Hongxing Zhang; Dual motor drive vehicle speed synchronization and coordination control strategy. AIP Conference Proceedings 2018, 1955, 040005, 10.1063/1.5033669.
- Yanjuan Wu; Yanbin Cheng; Yunliang Wang; Research on a Multi-Motor Coordinated Control Strategy Based on Fuzzy Ring Network Control. IEEE Access 2020, 8, 39375-39388, 10.1109/access.2020.2974906.
- Ganiev, R. Reversible frequency converters in the composition of multimotor electric drives. IOP Conf. Series: Mater. Sci. Eng. 2019, 643, 012068.
- Yanbo, C.; Lin, S.; Cheng, K.W.E. Variable Gain Intelligent Control of Multi-motor Synchronization System. In Proceedings of the 2006 2nd International Conference on Power Electronics Systems and Applications, Hong Kong, China, 12–14 November 2006; pp. 68–72.
- Valenzuela, M.A.; Lorenz, R.D. Electronic line-shafting control for paper machine drives. In Proceedings of the Conference Record of 2000 Annual Pulp and Paper Industry Technical Conference, Atlanta, GA, USA, 19–23 June 2000; pp. 106–112.
- De Chao Gao; Fang He; Fuzzy Coordinated Control for Multi-Motor Drive System. Applied Mechanics and Materials 2014, 631, 676-679, 10.4028/www.scientific.net/amm.631-632.676.
- Ran Liu; Jian Zhong Sun; Ya Qin Luo; Wei Sun; Wei Dong Li; Research on Multi-Motor Synchronization Control Based on the Ring Coupling Strategy for Cutterhead Driving System of Shield Machines. Applied Mechanics and Materials 2011, , , 10.4028/www.scientific.net/amm.52-54.65.
- Zhilong Huang; Yiming Li; Guiqiu Song; Xueliang Zhang; Zhongchao Zhang; Speed and Phase Adjacent Cross-Coupling Synchronous Control of Multi-Exciters in Vibration System Considering Material Influence. IEEE Access 2019, 7, 63204-63216, 10.1109/access.2019.2916983.
- N. Mitrovic; V. Kostić; Milutin Petronijevic; B. Jeftenic; Multi-Motor Drives for Crane Application. Advances in Electrical and Computer Engineering 2009, 9, 57-62, 10.4316/aece.2009.03011.
- Tinh, T.X.; Thanh, P.T.; Van Tuyen, T.; Van Tien, N.; Dao, P.N. A fuzzy adaptive sliding mode controller for uncertain nonlinear multi motor systems. In MATEC Web of Conferences; EDP Sciences: Ulis, France, 2018; Volume 161, p. 02013.
- Daniela Perduková; Pavol Fedor; Viliam Fedák; Sanjeevikumar Padmanaban; Lyapunov Based Reference Model of Tension Control in a Continuous Strip Processing Line with Multi-Motor Drive. Electronics 2019, 8, 60, 10.3390/electronics8010060.
- N.R. Abjadi; J. Askari; J. Soltani; G.R. Arab Markadeh; Nonlinear sliding-mode control of a multi-motor web-winding system without tension sensor. IET Control Theory & Applications 2009, 3, 419-427, 10.1049/iet-cta.2008.0118.
- Changfan Zhang; Mingjie Xiao; Jing He; Multimotor Improved Relative Coupling Cooperative Control Based on Sliding-Mode Controller. Mathematical Problems in Engineering 2020, 2020, 1-10, 10.1155/2020/5638462.
- Ángel Jiménez-Fernández; Gabriel Jiménez-Moreno; Bernabé Linares-Barranco; Manuel Domínguez-Morales; Rafael Paz Vicente; Antón Civit-Breu; A Neuro-Inspired Spike-Based PID Motor Controller for Multi-Motor Robots with Low Cost FPGAs. Sensors 2012, 12, 3831-3856, 10.3390/s120403831.
- Almeida, S.; Araujo, R.E. Fault-tolerant control using sliding mode techniques applied to multi-motor electric vehicle. In Proceedings of the IECON 2013-39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 3530–3535.
- Alexandre Silveira; Rui Esteves Araújo; Ricardo De Castro; Survey on Fault-Tolerant Diagnosis and Control Systems Applied to Multi-motor Electric Vehicles. Towards the Knowledge Society 2011, , , 10.1007/978-3-642-19170-1_39.
- De Castro, R.; Araujo, R.E.; Oliveira, H. Control in Multi-Motor Electric Vehicle with a FPGA platform. In Proceedings of the 2009 IEEE International Symposium on Industrial Embedded Systems, Lausanne, Switzerland, 8–10 July 2009; pp. 219–227.
- Deliang Yu; Wensong Wang; Huibo Zhang; Dongyue Xu; Research on Anti-Lock Braking Control Strategy of Distributed-Driven Electric Vehicle. IEEE Access 2020, 8, 162467-162478, 10.1109/access.2020.3021193.
- Mehmet Özger; Comparison of fuzzy inference systems for streamflow prediction. Hydrological Sciences Journal 2009, 54, 261-273, 10.1623/hysj.54.2.261.
- Oscar Cordón; A historical review of evolutionary learning methods for Mamdani-type fuzzy rule-based systems: Designing interpretable genetic fuzzy systems. International Journal of Approximate Reasoning 2011, 52, 894-913, 10.1016/j.ijar.2011.03.004.
- Hadjili, M.L.; Kara, K. Modelling and control using Takagi-Sugeno fuzzy models. In Proceedings of the 2011 Saudi International Electronics, Communications and Photonics Conference (SIECPC), Riyadh, Saudi Arabia, 24–26 April 2011; pp. 1–6.
- Jian-Xin Xu; Chang-Chieh Hang; Chen Liu; Parallel structure and tuning of a fuzzy PID controller. Automatica 2000, 36, 673-684, 10.1016/s0005-1098(99)00192-2.
- Liang Tao; Qiang Chen; Yurong Nan; Fang Dong; Yan Jin; Speed Tracking and Synchronization of a Multimotor System Based on Fuzzy ADRC and Enhanced Adjacent Coupling Scheme. Complexity 2018, 2018, 1-16, 10.1155/2018/5632939.
- Radu-Emil Precup; Radu-Codrut David; Emil M. Petriu; Stefan Preitl; Mircea-Bogdan Radac; Fuzzy Control Systems With Reduced Parametric Sensitivity Based on Simulated Annealing. IEEE Transactions on Industrial Electronics 2011, 59, 3049-3061, 10.1109/TIE.2011.2130493.
- Leposava B. Ristic; Borislav I. Jeftenic; Implementation of Fuzzy Control to Improve Energy Efficiency of Variable Speed Bulk Material Transportation. IEEE Transactions on Industrial Electronics 2011, 59, 2959-2969, 10.1109/tie.2011.2169639.
- Salem, F.; Bayoumi, E.H.E. Robust Fuzzy-PID Control of Three-Motor Drive System Using Simulated Annealing Optimization. IEEE Trans. Ind. Electron. 2013, 3, 284–292.
- Tian, Z.; Li, S.; Wang, Y.; Zang, Q. Multi Permanent Magnet Synchronous Motor Synchronization Control based on Variable Universe Fuzzy PI Method. Eng. Lett.
- Hui, L.; Xingqiao, L.; Jing, L. The research of Fuzzy Immune Linear Active Disturbance Rejection Control Strategy for three-motor synchronous system. Control. Eng. Appl. Inform. 2015, 17, 50–58
- Samanta, D. Defuzzification Methods, Chapter 5, course Soft Computing Applications. Available online: https://cse.iitkgp.ac.in/~dsamanta/courses/archive/sca/Archives/Chapter%205%20Defuzzification%20Methods.pdf
- Li, M.; Meng, X. Analysis and Design of System for Multi-motor Synchronous Control. In Proceedings of the Neural Networks for Modelling and Control of Dynamic Systems, Wuhan, China, 21–22 August 2011; pp. 268–273
- Ataei, E.; Afshari, R.; Pourmina, M.A. Fuzzy Logic Control of a Multifingered Hand Robot Using Genetic Algorithm Based on DSP. Int. Rev. Autom. Control. 2011, 4, 1–6.
- Lin Tang; Xing Qiao Liu; Li Ting Zhu; Study on Three-Motor Synchronous System of Fuzzy Active Disturbance Rejection Control. Applied Mechanics and Materials 2012, 224, 543-546, 10.4028/www.scientific.net/amm.224.543.
- Cuifeng Shen; Hanhua Yang; A New Three-Motor Drive System Using Fuzzy Active Disturbance Rejection Control. Automatic Control and Computer Sciences 2020, 54, 207-215, 10.3103/s0146411620030086.
- Hu, Y.; Sun, Z.; Zhou, H. Research on Improved Deviation Coupling AGV Multi-motor Coordinated Drive Control Based on PSO-Fuzzy. In Proceedings of the 2019 4th International Conference on Automatic Control and Mechatronic Engineering, Chongqing, China, 30–31 May 2019; pp. 185–189.