Distribution System State Estimation Algorithms: History
View Latest Version
Please note this is an old version of this entry, which may differ significantly from the current revision.
Contributor:
Maria Fotopoulou
,
Stefanos Petridis
,
Ioannis Karachalios
,
Dimitrios Rakopoulos

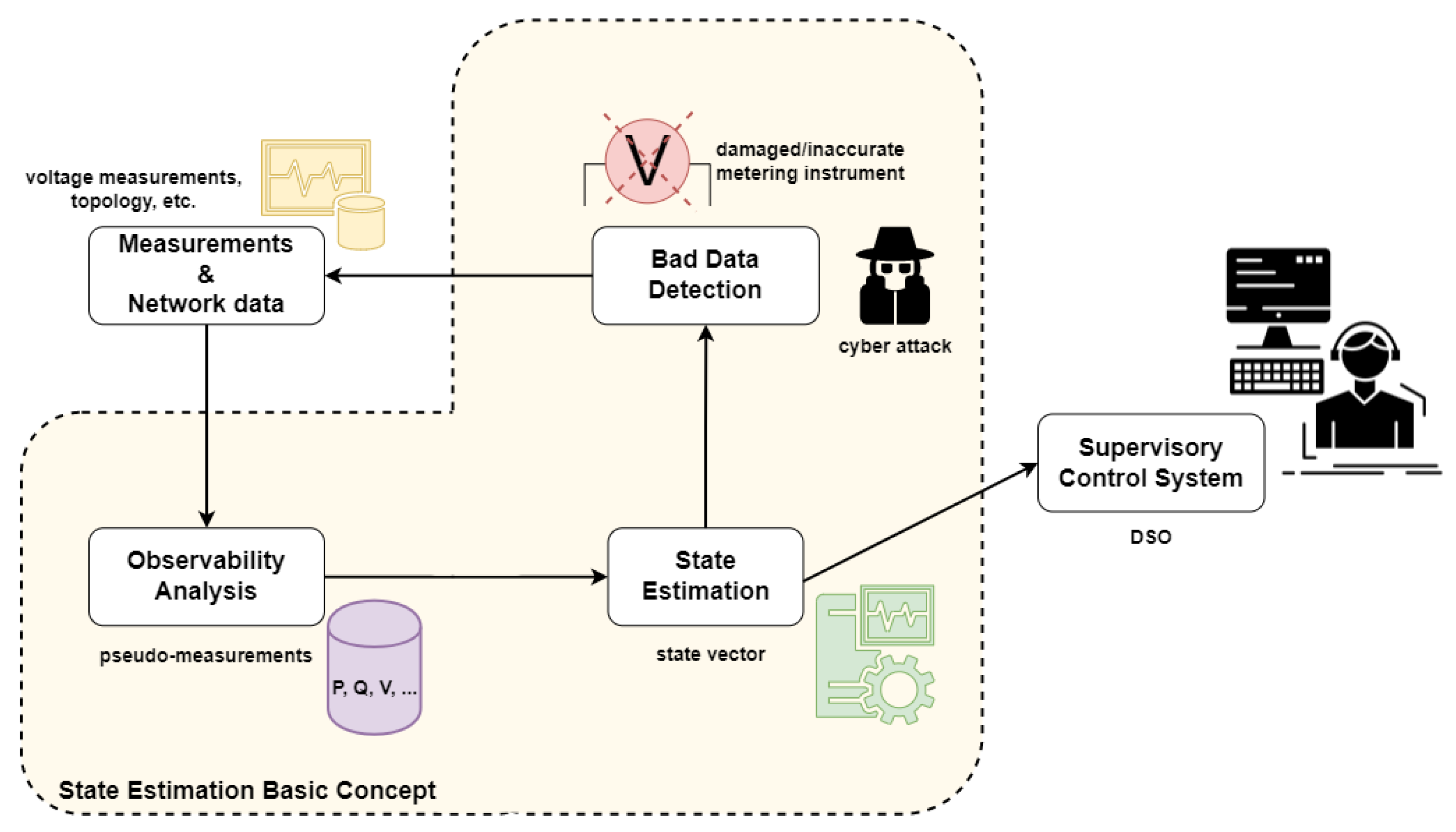
The modern energy requirements and the orientation towards Renewable Energy Sources (RES) integration promote the transition of distribution grids from passive, unidirectional, fossil fuel-based into active, bidirectional, environmental-friendly architectures. For this purpose, advanced control algorithms and optimization processes are implemented, the performance of which relies on the Distribution System State Estimation (DSSE). DSSE algorithms provide the Distribution System Operator (DSO) with detailed information regarding the network’s state in order to derive the optimal decisions. However, this task is quite complex as the distribution system has inherent unbalance issues, often faces lack of adequate measurements, etc.

  • distribution system state estimation (DSSE)
  • smart grid
  • unbalanced grid

1. Introduction

Over the past few decades, in order to support the ongoing energy transition, the concept of the electrical network has gradually changed [1]. More specifically, for the purpose of sustainability and the enhancement of autonomy, Renewable Energy Sources (RES), storage systems and other environmental-friendly technologies have emerged, the implementation of which has transformed both Medium Voltage (MV) and Low Voltage (LV) distribution systems [2][3]. Hence, passive, fuel-based distribution is challenged by more active, viable, and decentralized concepts [4].
In order to support the operation of modern distribution systems, the Distribution System Operator (DSO) utilizes a variety of algorithms that provide the optimal results and decisions [5]. Naturally, in many cases, the input of the aforementioned algorithms relies heavily on the accurate and detailed monitoring of the system’s status [6]. Consequently, an intermediate process between the acquisition of the system’s available measurements and the use of control and decision-support algorithms is required. This process, i.e., Distribution System State Estimation (DSSE), constitutes an asset of great importance for the DSO as it can be used for multiple purposes, including loss monitoring, load and RES profile creation, detection of voltage limit violations and asymmetry, fault localization, outage handling, etc., as presented in Figure 1 [7].
/media/item_content/202301/63d8d2e936024applsci-12-11073-g001.png
Figure 1. The value of DSSE for the DSO.
Overall, DSSE has evolved into a research field that has gathered the interest of many experts. More specifically, accurate and efficient DSSE is considered to be a complex task, not only due to the inherent unbalances of MV and LV grids, but also due to the lack of measurements, which may cause observability issues, as well as the possible existence of bad data (either caused by damaged/inaccurate metering instruments or by cyber-attacks) that need to be identified and excluded from the estimation, as presented in Figure 2 [8]. The aforementioned challenges may be approached in a variety of ways, usually through model-based or through more recently developed, data-driven strategies, providing a pool of multifarious solutions regarding DSSE implementation [9].
/media/item_content/202301/63d8d2f80dda5applsci-12-11073-g002.png
Figure 2. Basic concept of DSSE implementation.

2. DSSE Special Attributes

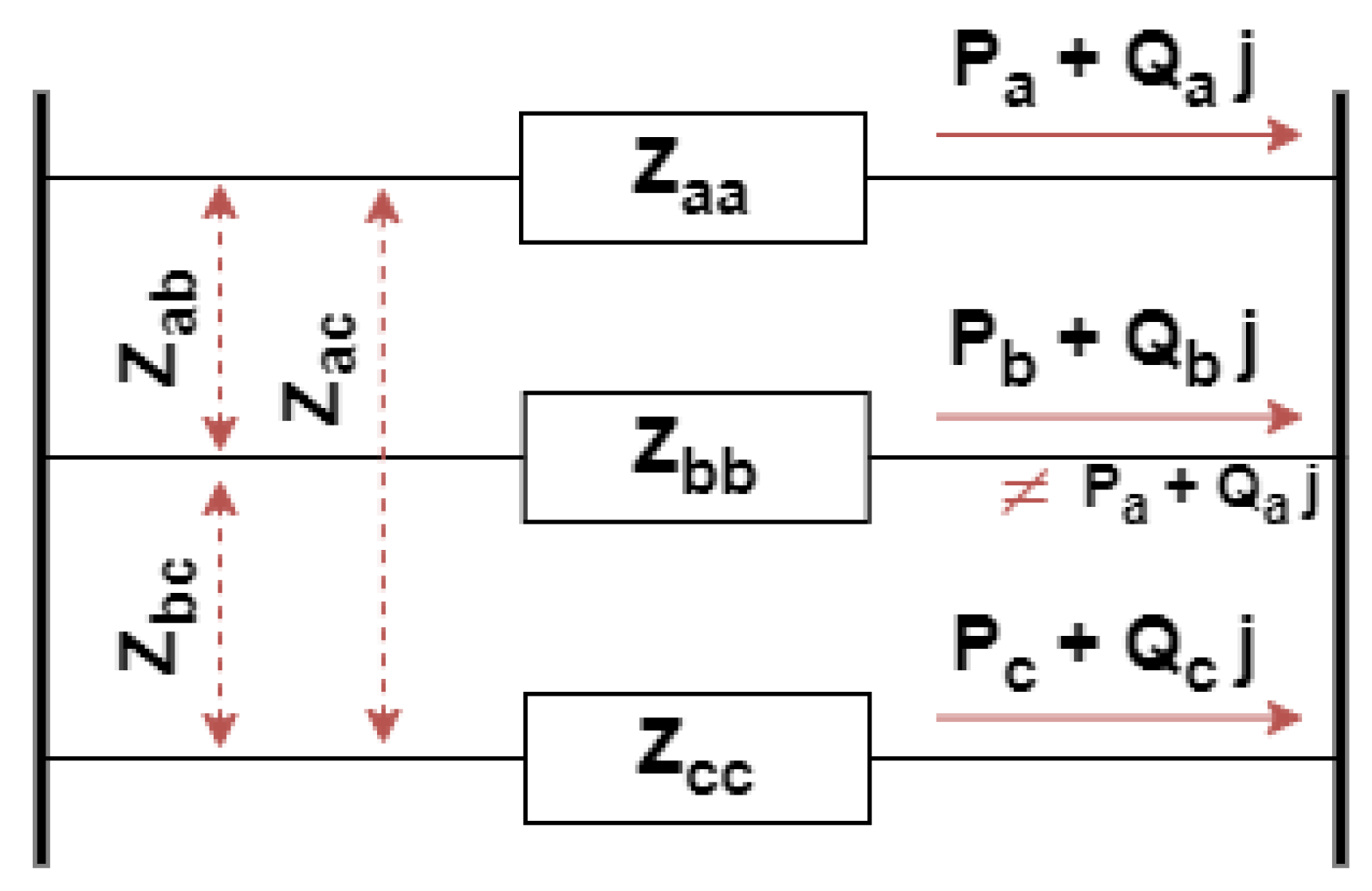
Distribution systems have a number of special attributes that render their detailed representation more complex than transmission systems. Firstly, distribution systems are unbalanced by nature, as presented in Figure 3. This is a result of the unbalanced consumption as well as the existence of mutual impendences between the lines. It should be noted that in some parts of the grid, phases may be missing by design, according to the requirements and geographical location of the loads, thereby enhancing the occurring unbalances. Thus, the modelling of the components, including lines, transformers, loads, etc., as well as the power flow equations, need to be adjusted. For example, the impendence matrix of a distribution line is formulated as presented in (1), where Z is the impendence [10]. Furthermore, the active and reactive power flow between two nodes is formulated as presented in (2) and (3), respectively, and the power injection is formulated as presented in (4) and (5), where Pphi,j and Qphi,j are the active and reactive power, respectively, flowing in phase ph between nodes i and j, Pphi and Qphi are the active and reactive power injection, respectively, in phase ph at node i, V is the voltage magnitude and δ is the voltage angle, G and B refer to the real and imaginary parts of the admittance matrix, respectively, l is the index referring to each of the three phases of the line, and n refers to the number of neighboring nodes [11][12]. The complexity of these formulas lies in the separate calculation of each phase’s values, as the occurring unbalances cannot be modelled via single-phase equivalent approaches [11][12]. 

  Z = [ Z aa Z ab Z ac Z ba Z bb Z bc Z ca Z cb Z cc ] .

P i , j ph = V i ph ∑ l = 1 3 V i l [ G i , j ph , l cos ( δ i ph − δ i l ) + B i , j ph , l sin ( δ i ph − δ i l ) ]                         − V i ph ∑ l = 1 3 V j l [ G i , j ph , l cos ( δ i ph − δ j l ) + B i , j ph , l sin ( δ i ph − δ j l ) ]

Q i , j ph = − V i ph ∑ l = 1 3 V i l [ G i , j ph , l sin ( δ i ph − δ i l ) − B i , j ph , l cos ( δ i ph − δ i l ) ]                         − V i ph ∑ l = 1 3 V j l [ G i , j ph , l sin ( δ i ph − δ j l ) − B i , j ph , l cos ( δ i ph − δ j l ) ]

P i ph = V i ph ∑ l = 1 3 ∑ j = 1 n V j l [ G i , j ph , l cos ( δ i ph − δ j l ) + B i , j ph , l sin ( δ i ph − δ j l ) ]

Q i ph = V i ph ∑ l = 1 3 ∑ j = 1 n V j l [ G i , j ph , l sin ( δ i ph − δ j l ) − B i , j ph , l cos ( δ i ph − δ j l ) ]
/media/item_content/202301/63d8d5643a0e8applsci-12-11073-g003.png
Figure 3. Unbalanced phases in the distribution system.
Another issue that the distribution systems face is the limited availability of real-time data as a result of the sparse meter placement. Therefore, the accuracy or even the convergence of the DSSE might be negatively affected. This is an issue that can be tackled either with the placement of more instruments, which provide the DSSE with more accuracy but have a certain cost, or with the use of pseudo-measurements [13]. Pseudo-measurements are used to augment the available real measurements and are usually calculated using short-term forecasts or historical data. As a result, they are not as accurate as an actual measurement, however they require no further actions or cost from the side of the DSO [14].
An additional factor that adds complexity to the DSSE is the configuration of the system. First and foremost, a modern, universal DSSE needs to be adaptable and equally efficient in all sorts of configurations–not just radial (which is the conventional use case) [15]. For example, the integration of RES and various innovative architectures in the MV and LV levels has promoted the research and development on ring and/or meshed configurations. Moreover, for reasons related to the increase of the system’s reliability, interconnected configurations (with more than one feeder) are studied. Other than the type of configuration, the status of the switches might sometimes be vague to the DSO, as they are not always monitored. In distribution networks, switches are mostly used in order to isolate a fault or mitigate congestion issues in the distribution system. A close switch of phase ph between nodes i and j is modeled as presented in (6)–(7), and an open switch is modeled as presented in (8)–(9) [11]. 
V i ph − V j ph = 0
V i ph − V j ph = 0
P i , j ph = 0
Q i , j ph = 0

3. DSSE Fundamentals and Main Algorithms

3.1. State Vectors

The state vector of the system is defined as a set of variables, which, unlike transmission systems, may be either Node-Voltage (NV)-based, i.e., NV-DSSE, or Branch-Current (BC)-based, i.e., BC-DSSE [16]. As there is no standard process, the selection of the appropriate state vector can be determined by the criteria presented in Table 1, which compares the two state vector options in terms of applicability, complexity, efficiency, and compatibility.
NV-DSSE includes the voltages of each node and can be formed using either polar or rectangular coordinates. These state vectors are the most common in literature and also constitute the default state vectors of transmission systems [17][18]. Their main advantage, aside from their wide implementation and rich literature analysis, is that they can be used for all sorts of configurations [19], such as radial, mesh, etc. In addition, this sort of state vector is recommended for the easy incorporation of voltage measurements. However, it is noted that NV-DSSE is highly sensitive to measurement weights and is likely to face convergence issues [20]. Work related to NV-DSSE can be found in [11][21][22] using polar coordinates and in [19][23] using rectangular coordinates.
BC-DSSE includes the currents of each branch and is usually formed using rectangular coordinates but can be also formed using polar coordinates [24][25]. For these state vectors, power measurements are expressed in terms of branch currents, and their use is recommended as a more straightforward process, especially when it comes to current measurements [9][26]. Even though BC-DSSE is mostly suitable for radial distribution networks, which is a major limitation, it should be mentioned that it is considered to have simple implementation, lower computational time, lower sensitivity (to measurement weights, etc.), and higher possibility to converge, compared to NV-DSSE [16][26].

3.2. DSSE Algorithms

3.2.1. Conventional, Model-Based Algorithms

The most common approach regarding the core of DSSE is the Weighted Least Square (WLS) algorithm. This is a model-based solution, denoting that the details of the distribution network need to be known to the operator beforehand. The purpose of WLS is to minimize the weighted residuals between the estimated and measured values, subjected to the distribution network’s constraints. Provided that the residual vector r is calculated with (10), where z is the measurement vector, x is the state vector, and h(x) is the measurement function calculated upon x, the objective function of the WLS is presented in (11). In the objective function, W is the weight matrix that denotes the operator’s confidence in the measured data. It should be noted that the size of z is (m × 1) where m refers to the number of measurements, the size of x is (n × 1) where n refers to the number of states, and the size of W is (m × m). Obviously, m can only be lower than (or equal to) n. 

r = z   −   h ( x )

r = z   −   h ( x )

Another advanced and robust model-based approach is the Least Trimmed Squares (LTS). In this case, the squared values of the residuals are calculated and ordered from the lowest to the highest. The objective function aims to select a total number, u, of lowest values and minimize their sum, as presented in (14). Related work can be found in [27]. 

  r = z   −   h ( x )

3.2.2. Forecasting-Aided Algorithms

The aforementioned conventional DSSE algorithms rely on a single set of measurements, taken on a certain moment. In this way, the evolution of the states over successive measurements is disregarded. The solution to this issue is the use of Forecasting-Aided State Estimation (FASE) [28][29]. The basic concept of FASE is to provide recursive updates of the estimated states. By these means, changes occurring during normal operation can be tracked. Moreover, since FASE is based on forecasts by nature, the usual problem of missing measurements can be addressed with the use of the forecasted states.
x ( k + 1 ) = F ( k ) x ( k ) + g ( k ) + w ( k )
In these sort of algorithms, Kalman-based filters are adopted to capture the dynamics of the distribution system. A typical dynamic model is presented in (17), where k is the time instant, F(k) is the is (n × n) state transition matrix, g(k) denotes the trend behavior of the state trajectory, with size equal to (n × 1), and w(k), the size of which is also equal to (n × 1), models the noise, which is usually assumed to follow a Gaussian distribution with zero mean [28]. 

3.2.3. Data-Driven Algorithms

Due to the ascending amalgamation of Information Technologies (IT) in the energy sector, data-driven algorithms have gained popularity in the field of state estimation over the past few years [30]. A major advantage of data-driven algorithms is that they assist in overcoming the issues that are encountered in other DSSE algorithms, which depend on parameters and models of distribution networks, are complicated, time-consuming, and very sensitive to initial conditions. Nevertheless, it should be highlighted that for this purpose a significant amount of data are required [31][32].
In literature, there is a variety of Artificial Intelligence (AI) and Machine Learning (ML) approaches including: (i) supervised, (ii) unsupervised, and (iii) reinforcement learning [33] that are also utilized in several fields of study [34][35]. In supervised learning, a labeled dataset, including input data and their corresponding output, is required. In the training phase of the algorithm, the relation between the provided inputs and outputs is defined as a function. Artificial Neural Networks (ANN), the popularity of which is increased, fall in this sort of learning. In addition, it should be highlighted that a well-known sub-category of ANN are the Deep Neural Networks (DNN), which in contrast to simple ANN have more than one hidden layer. On the other hand, in unsupervised learning, there are no complete and clean-labeled datasets. This is a sort of learning that finds previously unknown patterns in datasets and discovers the output. Finally, reinforcement learning is based on the interaction with the environment. In this case, an agent interacts with the environment by performing actions and learns either from errors or rewards [36].

4. Auxiliary Algorithms

4.1. Observability

The limited availability of real time data may challenge the observability of the distribution system. In order to provide the DSSE with enough data to converge and produce accurate results, pseudo-measurements are used [37]. Pseudo-measurements can be generated in a variety of ways. In literature, two main categories are distinguished, i.e., (i) probabilistic and statistical approaches and (ii) learning-based approaches [9][16].
Following probabilistic and statistical approaches, the authors of [38][39][40] have used Gaussian Mixture Models (GMM) and Expectation Maximization (EM). The Gaussian mixture, f(z|γ), comprises a weighted, finite sum of Gaussian probability density functions, f(z|μi,Σi), as presented in (18), where Mc is the number of mixture components. EM is used in order to obtain the parameters of the mixture components, i.e., weights, means, and variances, as presented in [41]. 
f ( z | γ ) = ∑ i = 1 M c w i   f ( z | μ i , Σ i )
Another way to obtain pseudo-measurements that falls into the category of probabilistic and statistical approaches is presented in [40] and involves the calculation of correlation coefficients between measurements obtained from the main substation and non-monitored electrical quantities and the application of regression analysis. The authors also compare the results provided by the correlation approach to the respective ones provided by the GMM.

4.2. Bad Data Detection

Bad data detection is of substantial importance for successfully estimating the system’s true state. Bad data can stem from: (i) erroneous measuring data [42], (ii) system faults [43], and (iii) False Data Injection Attacks (FDIAs) [44][45][46][47]. Thus, the discovery of false data can also help DSOs identify possible attacks in their system.

Model-based detection algorithms are prediction methods that measure the similarity between the predicted states and the actual field measurements. In literature, model-based bad data detection algorithms are used extensively. In [48][49][50][51][52][53] the authors use the L2-norm that is the Euclidean distance of the residual and compare it to a certain threshold as presented in (19), where measurement zi is considered faulty when its Euclidean distance from its respective calculation upon the predicted state, h(xi), is greater than the threshold, e.

  P L 2 ( z i ) = { 1 ,   if   ‖ z i − h ( x i ) ‖ 2   >   e 0 ,         otherwise

4.3. Meter Placement

The meter placement in a distribution system constitutes a key decision problem. For this purpose, three main sorts of algorithms are distinguished: (i) rule-based, (ii) metaheuristic, and (iii) optimization with an objective function subjected to a set of constraints [54]. In more detail, rule-based algorithms comprise of a number of rules that lead to the easy and fast solution of a problem at the cost of providing non-optimal solutions. Metaheuristic algorithms are usually bio-inspired and more evolved than rule-based algorithms. Indicative examples are Particle Swarm Optimization (PSO), Tabu Search (TS), etc. [55]. By using these sort of algorithms, sufficiently good solutions can be obtained but global optimality is not guaranteed. However, the most recent trends indicate the use of optimizers, which aim to maximize/minimize an objective function, limited by constraints, in order to obtain the optimal solution [56]. The main idea is to model constraints such as energy balances, power flows, voltage limitations, etc., and create a space for possible/feasible decisions. The purpose is to find the optimal set of decisions that maximizes/minimizes the value of the objective function. These problems can be Mixed Integer Linear Programming (MILP), Mixed Integer Nonlinear Programming (MINLP), etc., depending on the nature of t

The metering devices send measurement information to the Supervisory Control and Data Acquisition (SCADA) system under the IEC 60,870 communication protocol [57]. The SCADA is a control system architecture that contains computing devices, databases, and various interfaces that enable the real time monitoring and control of a distribution system [58]. Data-driven approaches of DSSE as well as algorithms associated with DSSE, such as forecasting models for pseudo-measurement creation and bad data detection, need large amounts of historical data to be trained and function properly. Thus, databases of SCADA, capable to perform DSSE, must be able to hold years of hourly or sub-hourly power, voltage, and current data [59].he problem [60].

5. Technical Requirements and Applications

5.1. Technical Requirements

It is evident that the most important requirement for a DSSE algorithm is the availability of measurements. Installing metering devices on a system is a necessary step for monitoring its performance and achieve the desired observability [61]. For having an accurate and up to date representation of the network, DSSE needs to be applied at least once for every hour of the day, so new measurements are needed for every new application of the algorithm. For example, the authors of [62] apply the DSSE in 10 min intervals, and in [63] the algorithm is performed every 30 min. The most common measuring components found in distribution systems are Phasor Measurement Units (PMUs) and Smart Meters (SM) [64][65][66]. PMUs offer synchronous power, voltage, and current measurements, as well as phase angles. SMs, on the other hand, record information such as energy consumption, voltage levels, current, and power factor. In specific distribution systems where only SMs exist and, consequently, no information concerning the phase angles, DSSE algorithms have to make assumptions about phase angle computation [67][68][69].
The metering devices send measurement information to the Supervisory Control and Data Acquisition (SCADA) system under the IEC 60,870 communication protocol [57]. The SCADA is a control system architecture that contains computing devices, databases, and various interfaces that enable the real time monitoring and control of a distribution system [58]. Data-driven approaches of DSSE as well as algorithms associated with DSSE, such as forecasting models for pseudo-measurement creation and bad data detection, need large amounts of historical data to be trained and function properly. Thus, databases of SCADA, capable to perform DSSE, must be able to hold years of hourly or sub-hourly power, voltage, and current data [59].

5.2. Applications

Regarding the applications of DSSE in distribution systems, research is mostly focused on RES penetration and “green” technologies, due to the ongoing energy transition. In this sense, it is quite common to find studies where DSSE is performed on distribution systems with high PV penetration.

Regarding the applications of DSSE in distribution systems, research is mostly focused on RES penetration and “green” technologies, due to the ongoing energy transition. In this sense, it is quite common to find studies where DSSE is performed on distribution systems with high PV penetration. For example, the authors of [70] have performed DSSE in a distribution system with PVs using a typical WLS algorithm. Similar concepts have been studied by [71][72], with the use of a variation of WLAV and a variation of EKF, respectively. Moreover, ref. [73] has performed DSSE in a distribution system that includes not only PVs but also Wind Turbines (WTs). In this case, the DSSE utilizes a DNN. In a more interesting scenario, ref. [74] has performed DSSE in a hybrid AC/DC system including PVs, WTs and diesel generators. The estimation is performed with the use of WLS, supported by a DNN. Finally, in a slightly different direction, the authors of [75] perform DSSE in a distribution system that is used to charge Electric Vehicles (EVs). For this purpose, a variation of the EKF is deployed.

6. Conclusions

Overall, it is concluded that:
  • WLS is the most commonly used algorithm, not only in theoretical development but also in actual applications.
  • Data-driven algorithms challenge the dominance of model-based counterparts.
  • DSSE can play an important role in the ongoing energy transition, but in order to do so in a large scale, standardized solutions should be established.

This entry is adapted from the peer-reviewed paper 10.3390/app122111073

References

  1. Mah, D.N.-Y.; Wu, Y.-Y.; Ip, J.C.-M.; Hills, P.R. The role of the state in sustainable energy transitions: A case study of large smart grid demonstration projects in Japan. Energy Policy 2013, 63, 726–737.
  2. Mahmud, N.; Zahedi, A. Review of control strategies for voltage regulation of the smart distribution network with high penetration of renewable distributed generation. Renew. Sustain. Energy Rev. 2016, 64, 582–595.
  3. Das, C.K.; Bass, O.; Kothapalli, G.; Mahmoud, T.S.; Habibi, D. Overview of energy storage systems in distribution networks: Placement, sizing, operation, and power quality. Renew. Sustain. Energy Rev. 2018, 91, 1205–1230.
  4. Anjana, K.; Shaji, R. A review on the features and technologies for energy efficiency of smart grid. Int. J. Energy Res. 2018, 42, 936–952.
  5. Gust, G.; Biener, W.; Brandt, T.; Dallmer-Zerbe, K.; Neumann, D.; Wille-Haussmann, B. Decision Support for Distribution Grid Planning. In Proceedings of the 2016 IEEE International Energy Conference (ENERGYCON), Leuven, Belgium, 4–8 April 2016; pp. 1–7.
  6. Alassery, F. Advanced metering infrastructure smart metering based on cloud architecture for low voltage distribution networks in application of smart grid monitoring. Sustain. Comput. Inform. Syst. 2022, 35, 100747.
  7. Wang, G.; Giannakis, G.; Chen, J.; Sun, J. Distribution system state estimation: An overview of recent developments. Front. Inf. Technol. Electron. Eng. 2019, 20, 4–17.
  8. Watitwa, J.; Awodele, K. A Review on Active Distribution System State Estimation. In Proceedings of the 2019 Southern African Universities Power Engineering Conference/Robotics and Mechatronics/Pattern Recognition Association of South Africa (SAUPEC/RobMech/PRASA), Bloemfontein, South Africa, 28–30 January 2019; pp. 726–731.
  9. Primadianto, A.; Lu, C.-N. A Review on Distribution System State Estimation. IEEE Trans. Power Syst. 2017, 32, 3875–3883.
  10. Gómez-Expósito, A.; Conejo, A.J.; Cañizares, C.A. Electric Energy Systems: Analysis and Operation; CRC Press: Boca Raton, FL, USA, 2016; ISBN 978-1-4200-0727-5.
  11. Majumdar, A.; Pal, B.C. A three-phase state estimation in unbalanced distribution networks with switch modelling. In Proceedings of the 2016 IEEE First International Conference on Control, Measurement and Instrumentation (CMI), Kolkata, India, 8–10 January 2016; pp. 474–478.
  12. Hansen, C.; Debs, A. Power system state estimation using three-phase models. IEEE Trans. Power Syst. 1995, 10, 818–824.
  13. Xygkis, T.C.; Korres, G.N. Optimized Measurement Allocation for Power Distribution Systems Using Mixed Integer SDP. IEEE Trans. Instrum. Meas. 2017, 66, 2967–2976.
  14. Clements, K.A. The Impact of Pseudo-Measurements on State Estimator Accuracy. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–4.
  15. Baran, M.E.; Zhu, J.; Kelley, A.W. Meter Placement for Real-Time Monitoring of Distribution Feeders. In Proceedings of the Power Industry Computer Applications Conference, Salt Lake City, UT, USA, 7–12 May 1995; pp. 228–233.
  16. Dehghanpour, K.; Wang, Z.; Wang, J.; Yuan, Y.; Bu, F. A Survey on State Estimation Techniques and Challenges in Smart Distribution Systems. IEEE Trans. Smart Grid 2019, 10, 2312–2322.
  17. Sarada Devi, M.S.N.G.; Yesuratnam, G. Comparison of State Estimation Process on Transmission and Distribution Systems. In Advances in Decision Sciences, Image Processing, Security and Computer Vision; Satapathy, S.C., Raju, K.S., Shyamala, K., Krishna, D.R., Favorskaya, M.N., Eds.; Learning and Analytics in Intelligent Systems; Springer International Publishing: Cham, Switzerland, 2020; Volume 4, pp. 414–423. ISBN 978-3-030-24317-3.
  18. Kotha, S.K.; Rajpathak, B. Power System State Estimation using Non-Iterative Weighted Least Square method based on Wide Area Measurements with maximum redundancy. Electr. Power Syst. Res. 2022, 206, 107794.
  19. Gholami, M.; Tehrani-Fard, A.; Lehtonen, M.; Moeini-Aghtaie, M.; Fotuhi-Firuzabad, M. A Novel Multi-Area Distribution State Estimation Approach for Active Networks. Energies 2021, 14, 1772.
  20. Radhoush, S.; Bahramipanah, M.; Nehrir, H.; Shahooei, Z. A Review on State Estimation Techniques in Active Distribution Networks: Existing Practices and Their Challenges. Sustainability 2022, 14, 2520.
  21. Kotsonias, A.; Asprou, M.; Hadjidemetriou, L.; Kyriakides, E. State Estimation for Distribution Grids with a Single-Point Grounded Neutral Conductor. IEEE Trans. Instrum. Meas. 2020, 69, 8167–8177.
  22. Yao, Y.; Liu, X.; Li, Z. Robust Measurement Placement for Distribution System State Estimation. IEEE Trans. Sustain. Energy 2019, 10, 364–374.
  23. Lu, C.; Teng, J.; Liu, W.-H. Distribution system state estimation. IEEE Trans. Power Syst. 1995, 10, 229–240.
  24. Melo, I.D.; Pereira, J.L.; Ribeiro, P.F.; Variz, A.M.; Oliveira, B.C. Harmonic state estimation for distribution systems based on optimization models considering daily load profiles. Electr. Power Syst. Res. 2019, 170, 303–316.
  25. Wang, H.; Schulz, N. A Revised Branch Current-Based Distribution System State Estimation Algorithm and Meter Placement Impact. IEEE Trans. Power Syst. 2004, 19, 207–213.
  26. Ahmad, F.; Rasool, A.; Ozsoy, E.; Sekar, R.; Sabanovic, A.; Elitaş, M. Distribution system state estimation-A step towards smart grid. Renew. Sustain. Energy Rev. 2018, 81, 2659–2671.
  27. Weng, Y.; Negi, R.; Liu, Q.; Ilić, M.D. Robust state-estimation procedure using a Least Trimmed Squares pre-processor. In Proceedings of the ISGT 2011, Anaheim, CA, USA, 17–19 January 2011; pp. 1–6.
  28. Huang, Y.-F.; Werner, S.; Huang, J.; Kashyap, N.; Gupta, V. State Estimation in Electric Power Grids: Meeting New Challenges Presented by the Requirements of the Future Grid. IEEE Signal Process. Mag. 2012, 29, 33–43.
  29. Liu, H.; Hu, F.; Su, J.; Wei, X.; Qin, R. Comparisons on Kalman-Filter-Based Dynamic State Estimation Algorithms of Power Systems. IEEE Access 2020, 8, 51035–51043.
  30. Simpson, R.H. Power System Data Base Management. In Proceedings of the Conference Record of 2000 Annual Pulp and Paper Industry Technical Conference (Cat. No.00CH37111), Atlanta, GA, USA, 19–23 June 2000; pp. 79–83.
  31. Wang, Q.; Li, F.; Tang, Y.; Xu, Y. Integrating Model-Driven and Data-Driven Methods for Power System Frequency Stability Assessment and Control. IEEE Trans. Power Syst. 2019, 34, 4557–4568.
  32. Matijašević, T.; Antić, T.; Capuder, T. A systematic review of machine learning applications in the operation of smart distribution systems. Energy Rep. 2022, 8, 12379–12407.
  33. Sah, S. Machine Learning: A Review of Learning Types. Math. Comput. Sci. 2020.
  34. Sharma, P.; Said, Z.; Kumar, A.; Nižetić, S.; Pandey, A.; Hoang, A.T.; Huang, Z.; Afzal, A.; Li, C.; Le, A.T.; et al. Recent Advances in Machine Learning Research for Nanofluid-Based Heat Transfer in Renewable Energy System. Energy Fuels 2022, 36, 6626–6658.
  35. Rajamoorthy, R.; Arunachalam, G.; Kasinathan, P.; Devendiran, R.; Ahmadi, P.; Pandiyan, S.; Muthusamy, S.; Panchal, H.; Kazem, H.A.; Sharma, P. A novel intelligent transport system charging scheduling for electric vehicles using Grey Wolf Optimizer and Sail Fish Optimization algorithms. Energy Sources Part A Recover. Util. Environ. Eff. 2022, 44, 3555–3575.
  36. Dridi, S. Supervised Learning–A Systematic Literature Review. 2021. Available online: https://www.researchgate.net/publication/354996999_Supervised_Learning_-_A_Systematic_Literature_Review (accessed on 26 September 2022).
  37. Fantin, C.A.; Castillo, M.R.C.; de Carvalho, B.E.B.; London, J.B.A. Using Pseudo and Virtual Measurements in Distribution System State Estimation. In Proceedings of the 2014 IEEE PES Transmission & Distribution Conference and Exposition–Latin America (PES T&D-LA), Medellin, Colombia, 10–13 September 2014; pp. 1–6.
  38. Singh, R.; Pal, B.; Jabr, R. Distribution system state estimation through Gaussian mixture model of the load as pseudo-measurement. IET Gener. Transm. Distrib. 2010, 4, 50–59.
  39. Singh, R.; Pal, B.C.; Jabr, R.A. Statistical Representation of Distribution System Loads Using Gaussian Mixture Model. IEEE Trans. Power Syst. 2010, 25, 29–37.
  40. Manitsas, E.; Singh, R.; Pal, B.; Strbac, G. Modelling of Pseudo-Measurements for Distribution System State Estimation. In Proceedings of the CIRED Seminar 2008: SmartGrids for Distribution, Frankfurt, Germany, 23–24 June 2008; p. 42.
  41. Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum Likelihood from Incomplete Data via the EM Algorithm. J. R. Stat. Soc. Ser. B (Methodol.) 1977, 39, 1–22.
  42. Monticelli, A.; Garcia, A. Reliable Bad Data Processing for Real-Time State Estimation. IEEE Trans. Power Appar. Syst. 1983, PAS-102, 1126–1139.
  43. Manandhar, K.; Cao, X.; Hu, F.; Liu, Y. Detection of Faults and Attacks Including False Data Injection Attack in Smart Grid Using Kalman Filter. IEEE Trans. Control Netw. Syst. 2014, 1, 370–379.
  44. Liu, Y.; Ning, P.; Reiter, M.K. False data injection attacks against state estimation in electric power grids. ACM Trans. Inf. Syst. Secur. 2011, 14, 1–33.
  45. Rahman, M.A.; Mohsenian-Rad, H. False Data Injection Attacks against Nonlinear State Estimation in Smart Power Grids. In Proceedings of the 2013 IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5.
  46. Liang, G.; Zhao, J.; Luo, F.; Weller, S.R.; Dong, Z.Y. A Review of False Data Injection Attacks Against Modern Power Systems. IEEE Trans. Smart Grid 2017, 8, 1630–1638.
  47. Ayad, A.; Farag, H.E.Z.; Youssef, A.; El-Saadany, E.F. Detection of False Data Injection Attacks in Smart Grids Using Recurrent Neural Networks. In Proceedings of the 2018 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 19–22 February 2018; pp. 1–5.
  48. Kallitsis, M.G.; Bhattacharya, S.; Stoev, S.; Michailidis, G. Adaptive Statistical Detection of False Data Injection Attacks in Smart Grids. In Proceedings of the 2016 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Washington, DC, USA, 7–9 December 2016; pp. 826–830.
  49. Khalid, H.M.; Peng, J.C.-H. Immunity Toward Data-Injection Attacks Using Multisensor Track Fusion-Based Model Prediction. IEEE Trans. Smart Grid 2017, 8, 697–707.
  50. Xu, R.; Wang, R.; Guan, Z.; Wu, L.; Wu, J.; Du, X. Achieving Efficient Detection Against False Data Injection Attacks in Smart Grid. IEEE Access 2017, 5, 13787–13798.
  51. Sreenath, J.G.; Meghwani, A.; Chakrabarti, S.; Rajawat, K.; Srivastava, S.C. A recursive state estimation approach to mitigate false data injection attacks in power systems. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 1–5.
  52. Duan, J.; Zeng, W.; Chow, M.-Y. Resilient Distributed DC Optimal Power Flow Against Data Integrity Attack. IEEE Trans. Smart Grid 2018, 9, 3543–3552.
  53. Musleh, A.S.; Khalid, H.M.; Muyeen, S.M.; Al-Durra, A. A Prediction Algorithm to Enhance Grid Resilience Toward Cyber Attacks in WAMCS Applications. IEEE Syst. J. 2019, 13, 710–719.
  54. Camacho, E.F.; Bordons, C. Model Predictive Control: Advanced Textbooks in Control and Signal Processing, 2nd ed; Springer: London, UK; New York, NY, USA, 2004; ISBN 978-0-85729-398-5.
  55. Abdel-Basset, M.; Abdel-Fatah, L.; Sangaiah, A.K. Metaheuristic Algorithms: A Comprehensive Review. In Computational Intelligence for Multimedia Big Data on the Cloud with Engineering Applications; Elsevier: Amsterdam, The Netherlands, 2018; pp. 185–231. ISBN 978-0-12-813314-9.
  56. Pereira, J.L.J.; Oliver, G.A.; Francisco, M.B.; Cunha, S.S.; Gomes, G.F. A Review of Multi-objective Optimization: Methods and Algorithms in Mechanical Engineering Problems. Arch. Comput. Methods Eng. 2022, 29, 2285–2308.
  57. SCADA Communication and Protocols. Available online: https://instrumentationtools.com/scada-communication-and-protocols/ (accessed on 26 September 2022).
  58. Tomsovic, K.; Bakken, D.; Venkatasubramanian, V.; Bose, A. Designing the Next Generation of Real-Time Control, Communication, and Computations for Large Power Systems. Proc. IEEE 2005, 93, 965–979.
  59. Hippert, H.S.; Pedreira, C.E.; Souza, R.C. Neural networks for short-term load forecasting: A review and evaluation. IEEE Trans. Power Syst. 2001, 16, 44–55.
  60. Klanšek, U. A comparison between MILP and MINLP approaches to optimal solution of nonlinear discrete transportation problem. Transport 2014, 30, 135–144.
  61. El-Hawary, M.E. The Smart Grid—State-of-the-art and Future Trends. Electr. Power Compon. Syst. 2014, 42, 239–250.
  62. Croteau, D.; Carre, O. Distribution state estimation: Outcomes from a field implementation aimed at tackling MV mastering in the presence of distributed energy resources (DER). CIRED–Open Access Proc. J. 2017, 2017, 1715–1717.
  63. Al-Wakeel, A.; Wu, J.; Jenkins, N. State estimation of medium voltage distribution networks using smart meter measurements. Appl. Energy 2016, 184, 207–218.
  64. Pegoraro, P.A.; Tang, J.; Liu, J.; Ponci, F.; Monti, A.; Muscas, C. PMU and Smart Metering Deployment for State Estimation in Active Distribution Grids. In Proceedings of the 2012 IEEE International Energy Conference and Exhibition (ENERGYCON), Florence, Italy, 9–12 September 2012; pp. 873–878.
  65. Heydt, G.T. The Next Generation of Power Distribution Systems. IEEE Trans. Smart Grid 2010, 1, 225–235.
  66. Albu, M.; Heydt, G.T.; Cosmescu, S.-C. Versatile platforms for wide area synchronous measurements in power distribution systems. In Proceedings of the North American Power Symposium 2010, Arlington, TX, USA, 26–28 September 2010.
  67. Deka, D.; Backhaus, S.; Chertkov, M. Structure Learning in Power Distribution Networks. IEEE Trans. Control. Netw. Syst. 2015, 5, 1061–1074.
  68. Peppanen, J.; Reno, M.J.; Broderick, R.J.; Grijalva, S. Distribution System Model Calibration With Big Data From AMI and PV Inverters. IEEE Trans. Smart Grid 2016, 7, 2497–2506.
  69. Weng, Y.; Liao, Y.; Rajagopal, R. Distributed Energy Resources Topology Identification via Graphical Modeling. IEEE Trans. Power Syst. 2017, 32, 2682–2694.
  70. Bandara, W.G.C.; Almeida, D.; Godaliyadda, R.I.; Ekanayake, M.P.; Ekanayake, J. A complete state estimation algorithm for a three-phase four-wire low voltage distribution system with high penetration of solar PV. Int. J. Electr. Power Energy Syst. 2021, 124, 106332.
  71. Barchi, G.; Macii, D. A photovoltaics-aided interlaced extended Kalman filter for distribution systems state estimation. Sustain. Energy Grids Netw. 2021, 26, 100438.
  72. Song, S.; Xiong, H.; Lin, Y.; Huang, M.; Wei, Z.; Fang, Z. Robust three-phase state estimation for PV-Integrated unbalanced distribution systems. Appl. Energy 2022, 322, 119427.
  73. Menke, J.-H.; Bornhorst, N.; Braun, M. Distribution system monitoring for smart power grids with distributed generation using artificial neural networks. Int. J. Electr. Power Energy Syst. 2019, 113, 472–480.
  74. Huang, M.; Zhao, J.; Wei, Z.; Pau, M.; Sun, G. Decentralized robust state estimation for hybrid AC/DC distribution systems with smart meters. Int. J. Electr. Power Energy Syst. 2022, 136, 107656.
  75. Antončič, M.; Papič, I.; Blažič, B. Robust and Fast State Estimation for Poorly-Observable Low Voltage Distribution Networks Based on the Kalman Filter Algorithm. Energies 2019, 12, 4457.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
This entry is offline, you can click here to edit this entry!
ScholarVision Creations
Feedback